Obliczyć wartość siły H naciągającej przewód trakcji dla założonej odległości l między podporami
Wartość siły naciągającej przewód obliczamy ze wzoru 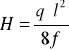
dla założonej odległości l między wieszakami możemy obliczyć maksymalną strzałkę ugięcia fmax oraz sprawdzić naprężenia w przewodzie na podstawie wzoru ![]()
Obliczyć naprężenia w przewodzie trakcji dla założonej odległości l między podporami
Gdy punkty zawieszenia leżą na różnych poziomach to po podstawieniu do wzoru
dla x = - a oraz x = b otrzymujemy odpowiednio 
Dla y x=a = f ![]()
oraz 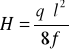
mając dane q , l i f można obliczyć siłę i naprężenia w cięgnach.
Warunek wytrzymałości cięgien o znanym przekroju porzecznym F
![]()
Równania równowagi - dla płaskiego i przestrzennego układu sił
by dowolny płaski układ sił znajdował się w równowadze zarówno wektor główny R jak i moment główny M muszą być równe zeru. Zatem składowe wektora R oraz suma momentów względem dowolnego punktu muszą być równe zeru. Warunki równowagi w przypadku płaskiego układu sił sprowadzają się do spełnienia układu równań.
![]()
![]()
![]()
Powyższe równania nazywamy równaniami równowagi dla płaskiego dowolnego układu sił.
Tarcie i prawa tarcia.
1. Wartość siły tarcia nie zależy od wielkości stykających się powierzchni, ale od ich rodzaju (rodzaj powierzchni, stan chropowatości itp.)
2. Wartość siły tarcia T zależy od nacisku normalnego i zawiera się w granicach
![]()
3. Zwrot siły tarcia jest przeciwny do zamierzonego kierunku ruchu
W przypadku ciała, którego wymiary są pomijalnie małe, tak że można je sprowadzić do punktu materialnego siły działające na ciało można w przybliżeniu potraktować jako układ sił zbieżnych. Równania równowagi, na podstawie których oblicza się współczynnik tarcia dla ciała umieszczonego na równi nachylonej pod kątem mają postać
![]()
![]()
![]()
skąd ![]()
Jeżeli kąt jest zmienny i równia jest nachylona pod takim kątem , przy którym ciało zaczyna się zsuwać, wówczas kąt ten nazywamy granicznym, a tangens jest równy współczynnikowi tarcia . Schemat ten wyjaśnia sens fizyczny współczynnika tarcia. Wówczas równania równowagi dla ciała, leżącego na równi nachylonej pod kątem mają postać
![]()
![]()
![]()
![]()
![]()
oraz ![]()
Środek sił równoległych - środki ciężkości.
Środek sił równoległych w odniesieniu do sił masowych nazywamy środkiem ciężkości. Dzieląc ciało na małe elementy o ciężarze Gi oraz wykorzystując równania sum momentów względem osi x, y i z otrzymujemy odpowiednio.
![]()
![]()
![]()
![]()
Tw. Guldina - Pappusa
Powierzchnia boczna bryły obrotowej utworzonej przez obrót płaskiej linii wokół osi leżącej w płaszczyźnie tej linii jest iloczynem drogi środka ciężkości tej linii (2xc) pomnożonej przez jej długość.
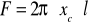
Objętość bryły obrotowej powstałej wskutek obrotu figury płaskiej dookoła osi leżącej w płaszczyźnie tej figury jest równa iloczynowi drogi środka ciężkości (2xc), powierzchni figury(F), przez jej powierzchnię.
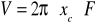
Naprężenia dopuszczalne
Naprężenia dopuszczalne, tzn. takie, które zapewniają bezpieczną pracę konstrukcji oblicza się na podstawie prób rozciągania lub ściskania.
![]()
![]()
(14.1)
Natomiast naprężenia dopuszczalne na ściskanie materiałów plastycznych otrzymujemy po podzieleniu granicy plastyczności Re przez współczynnik bezpieczeństwa n1
![]()
(14.2)
Podobnie naprężenia dopuszczalne na ściskanie dla materiałów kruchych (żeliwa, betonu) otrzymujemy po podzieleniu wytrzymałości na ściskanie Rc przez odpowiedni współczynnik bezpieczeństwa nc.
![]()
(14.3)
Umowna granica plastyczności - R0.2 - jest to naprężenie po osiągnięciu, którego powstaje odkształcenie trwałe równe 0.2 % długości początkowej.
Umowną granicę plastyczności obliczamy na podstawie badań wg wzoru
![]()
(14.4)
Gdzie: P0.2 - jest siłą odpowiadającą odkształceniu trwałemu tr = 0.2 %
F0 - jest pierwotnym przekrojem poprzecznym próbki
Prawo Hooke'a.
Podstawowym równaniem określającym zależność między naprężeniami σ i odkształceniami jest prawo Hooke'a. Prawo to znane z fizyki zapisujemy w postaci prostych wzorów.
![]()
albo ![]()
(15. 2)
ponieważ ![]()
to ![]()
lub ![]()
(15. 3)
gdzie: P - jest siłą rozciągającą
l - długością początkową, l - wydłużeniem pręta
F - pierwotnym przekrojem poprzecznym próbki
E - jest stałą charakteryzującą sprężystość materiału, nazywaną modułem sprężystości lub modułem Younga.
Moduł Younga E określany jako współczynnik charakteryzujący sprężystość materiału może kojarzyć się z liczbą bezwymiarową, tymczasem stała ta ma wymiar naprężenia. Jeżeli pręt o długości l będzie rozciągany naprężeniami σ = E, wówczas jego wydłużenie obliczone na postawie prawa Hooke'a wynosi ![]()
Zastosowanie podstawowych zasad mechaniki do obliczeń trakcji elektrycznych
Zasady obliczania sił w cięgnach (np. przewodach napowietrznych) opierają się na przyjęciu pewnych założeń upraszczających:
Dla cięgien silnie napiętych przyjmujemy, że kształt linii zwisu nie jest linią łańcuchową lecz parabolą.
Ponieważ cięgno ma być silnie napięte zatem jego długość mierzona po łuku niewiele będzie się różniła od cięciwy.
Ciężar cięgna przypadający na jednostkę długości q [N/m] traktujemy jako ciężar rzutu linii łańcuchowej na poziom i obliczamy wg wzoru
![]()
gdzie G - jest ciężarem cięgna, l - rozpiętością między podporamiw dowolnym punkcie cięgna siła
naciągu będzie skierowana wzdłuż stycznej do linii łańcuchowej .
Momenty bezwładności figur płaskich
Momentem bezwładności figury o polu F względem osi z nazywamy sumę iloczynów elementarnych pól dF przez kwadraty odległości od danej osi i zapisujemy całką ![]()
1. prostokąt o wymiarach b i h
Układ współrzędnych poprowadzono przez boki prostokąta.
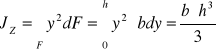
a) Układ współrzędnych poprowadzono przez środek ciężkości prostokąta
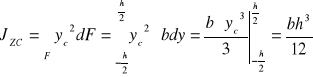
trójkąt o wymiarach b i h
![]()
![]()
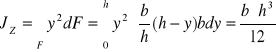
koło o promieniu r
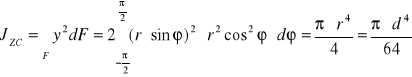
półkole o promieniu r
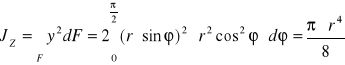
Obliczanie belek na zginanie
Siłą normalną N w danym przekroju poprzecznym belki nazywamy wypadkową rzutów na kierunek normalnej do płaszczyzny przekroju (zwykle osi belki) wszystkich sił zewnętrznych i reakcji więzów działających na część belki odciętą tym przekrojem.
Siłą tnącą T w danym przekroju poprzecznym belki nazywamy wypadkową rzutów na kierunek prostopadły do normalnej do płaszczyzny przekroju (zwykle prostopadły do osi belki) wszystkich sił zewnętrznych i reakcji więzów działających na część belki odciętą tym przekrojem.
Momentem gnącym Mg w danym przekroju poprzecznym belki nazywamy sumę momentów (względem środka ciężkości przekroju) wszystkich sił zewnętrznych i reakcji więzów działających na część belki odciętą tym przekrojem
równanie różniczkowe linii ugięcia belki
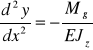
Maksymalne naprężenia przy zginaniu występują we włóknach skrajnych i wynoszą

Naprężenia te muszą być mniejsze od dopuszczalnych, zatem muszą spełniać warunek
σmax kg
Naprężeniami dopuszczalnymi na zginanie (lub na rozciąganie) nazywamy naprężenia, zapewniające bezpieczną pracę konstrukcji, oblicza się je ze wzoru
![]()
W praktycznych obliczeniach wprowadzono pojęcie wskaźnika przekroju. Wskaźnikiem przekroju nazywamy iloraz momentu bezwładności względem osi centralnej przez maksymalną odległość od osi przechodzącej przez środek ciężkości (zc) do włókien skrajnych.
![]()
Wówczas maksymalne naprężenia przy zginaniu obliczamy wg wzoru
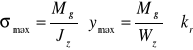
Skręcanie wałów o przekroju kołowym
Całkowity moment skręcający jest sumą momentów elementarnych i można go obliczyć na podstawie całki
![]()
albo ![]()
![]()
wzór na naprężenia przy skręcaniu ![]()
Maksymalne naprężenia przy skręcaniu występują we włóknach skrajnych dla ρmax = r
i wynoszą
![]()
gdzie ![]()
![]()
gdzie Jo - jest biegunowym momentem bezwładności
l - jest długością pręta
Wyszukiwarka
Podobne podstrony:
Mechanika i Wytrzymałość Materiałów zestaw2
Mechanika i Wytrzymałość Materiałów W 1
POMIAR TWARDOŚCI SPOSOBEM BRINELLA, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzy
Mechanika - 3cie kolokwium, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość m
mechanika - teoria, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość materiałó
Mechanika i Wytrzymałość Materiałów W 4
6.Tensometria(3), POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałość materiałów,
Mechanika i Wytrzymałość Materiałów zestaw3
Mechanika i Wytrzymałość Materiałów W 5
mechanika o wytrzymalosc materialow
Zagadnienia- mechanika, Politechnika Wrocławska Energetyka, 3 semestr, Mechanika i wytrzymałość mate
Wykłady i ćwiczenia mechanika, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzymałoś
WYZNACZANIE MOMENTU BEZWŁADNOŚCI I SPRAWDZANIE TWIERDZENIA STEINERA 12, Nauka, MECHANIKA I WYTRZYMAŁ
badania twardosci metoda vickersa, POLITECHNIKA POZNAŃSKA, LOGISTYKA, semestr I, mechanika i wytrzym
zagadnienia egzamin mechanika, Wytrzymałość materiałów i mechanika budowli (WMiMB)
MECHANIKATECHNICZNA I WYTRZYMAŁOŚĆ MATERIAŁOW STATYKA
MiWM (1), Polibuda, semestr 3, Mechanika i wytrzymałość materiałów, Mech. i wytrzymał. materiałów -
więcej podobnych podstron