Zadanie 1

W celu oszacowania przeciętnej punktacji na egzaminie ze statystyki na II roku studiów wylosowano z populacji studentów 12 osób i odnotowano ich wyniki w kolejności losowania:

88 60 90 87 48 44 47 46 36 64 66 85.

Przyjmując poziom istotności α = 0,1 zweryfikować hipotezę o losowości próby.

Test serii Stevensa

H0: dobór próby był losowy

H1: dobór próby nie był losowy

PROCEDURA POSTĘPOWANIA

1. Trzeba uszeregować ciąg niemalejący

36 44 46 47 48 60 64 66 85 87 88 90

2. Wyznaczyć medianę n = 12

Mediana jest pomiędzy 6, a 7 obserwacją

Me = 62

3. Tworzymy serie

x1 < Me a x2 ≥ Me b

b a b b a a a a a b b b

1 seria 2 seria 3 seria 4 seria 5 seria

4. Obliczamy ile jest serii

k - liczba serii k = 5

5. Porównuję z wartością krytyczną

k = 3 k = 5 k = 10

k₁ = k (0,05; 6; 6) = 3 k₂ = k (0,95; 6; 6) = 10

Interpretacja:

k₁ < k < k₂ Nie ma podstaw do odrzucenia hipotezy H₀ mówiącej o tym, że dobór prób był losowy.

Zadanie 2

Ze 100 wypraw rybackich kutra K wybrano 12, z dwóch rejonów połowów: N i P. Procent złowionych śledzi kształtował się następująco:

Rejon N	60,2	70,4	36,0	44,0	42,0	68,0	70,0	70,1	53,0	59,0	68,9	70,0
Rejon P	30,4	20,6	70,4	60,3	36,1	49,1	69,1	73,2	44,1	32,6	48,0	40,0

Za pomocą testu serii na poziomie istotności α = 0,05 zweryfikować hipotezę o nieistotnej różnicy w procencie złowionych śledzi w obu rejonach połowów.

Test serii Walda-Wolfowitza

H0: próby pochodzą z tej samej populacji		H0: F1(X) = F2(X)
H1: próby pochodzą z różnych populacji		H1: F1(X) ≠ F2(X)

H0: procenty złowionych śledzi w obu rejonach połowów N i P był taki sam

H1: procenty złowionych śledzi w obu rejonach połowów N i P statystycznie istotnie różnił się od siebie

PROCEDURA POSTĘPOWANIA

1. Zbudować niemalejący szereg dla każdej próby

Rejon N:

36,0 42,0 44,0 53,0 59,0 60,2 68,0 68,9 70,0 70,0 70,1 70,4

Rejon P

20,6 30,4 32,6 36,1 40,0 44,1 48,0 49,1 60,3 69,1 70,4 73,2

2. Tworzymy łączny szereg niemalejący

20,6^P 30,4^P 32,6^P 36,0^N 36,1^P 40,0^P 42,0^N 44,0^N 44,1^P 48,0^P 49,1^P 53,0^N

59,0^N 60,2^N 60,3^P 68,0^N 68,9^N 69,1^P 70,0^N 70,0^N 70,1^N 70,4^N 70,4^P 73,2^P

3. Zliczamy liczbę serii

k - liczba serii k = 11

4. Porównuję z wartością krytyczną

k_α = k (0,05; 12; 12) = 8

Interpretacja:

k > k_α Nie ma podstaw do odrzucenia hipotezy H₀ mówiącej o tym, że: procenty złowionych śledzi w obu rejonach połowów N i P był taki sam.

Zadanie 3

W lutym przeprowadzono badanie opóźnień dalekobieżnych pociągów pospiesznych, wyjeżdżających ze stacji S. Rejestrem objęto 15 wybranych losowo pociągów. Średni czas ich opóźnień wynosił (w min): 20, 25, 44, 60, 65, 40, 38, 120, 140, 80, 62, 40, 54, 48, 40. Komisja powołana do oceny wyników orzekła, iż opóźnienia są niedopuszczalnie wysokie i zarządziła reorganizację. Badanie powtórzono w maju. Tym razem otrzymano następujące wyniki: 18, 40, 60, 53, 41, 32, 100, 28, 46, 71, 64, 75, 32, 90, 49.

Za pomocą testu znaków zweryfikować hipotezę, że różnice w opóźnieniach pociągów są nieistotne. Przyjąć poziom istotności α = 0,01.

Test znaków

H0: próby pochodzą z tej samej populacji		H0: F1(X) = F2(X)
H1: próby pochodzą z różnych populacji		H1: F1(X) ≠ F2(X)

H0: różnice w opóźnieniach pociągów nie uległy zmianie na skutek reorganizacji

H1: różnice w opóźnieniach pociągów po reorganizacji statystycznie istotnie odbiegały od tych różnic przed reorganizacją

PROCEDURA POSTĘPOWANIA

1. Zapisujemy wyniki przed i po reorganizacji. Badamy znak różnicy.

przed	20	25	44	60	65	40	38	120	140	80	62	40	54	48	40
po	18	40	60	53	41	32	100	28	46	71	64	75	32	90	49
znak różnicy	−	+	+	−	−	−	+	−	−	−	+	+	−	+	+

Mamy 7 wzrostów i 8 spadków.

2. Wyznaczamy r

r - liczba tych znaków, których jest najmniej

3. Porównuję z obszarem krytycznym, r i r_α

r_α = r (α, n) = r (0,01; 15) = 2

r_α = 2 r = 7

Interpretacja:

r > r_α Nie ma podstaw do odrzucenia hipotezy H₀, mówiącej o tym, że różnice w opóźnieniach pociągów nie uległy zmianie na skutek reorganizacji.

Zadanie 4

Wylosowano niezależnie po 12 samochodów ciężarowych przyjeżdżających do Polski przez sąsiadujące z sobą przejścia graniczne w miejscowościach A i B. Czas oczekiwania na odprawę (w godzinach) był następujący:

- przejście A: 2, 5, 3, 3, 6, 1, 3, 5, 4, 6, 2, 6; - przejście B: 3, 5, 5, 8, 9, 4, 4, 7, 7, 8, 6, 8.

Wnioskując na poziomie istotności α = 0,05 zweryfikować za pomocą testu mediany hipotezę o jednakowym czasie oczekiwania na obu badanych przejściach granicznych.

Test mediany

H0: czas oczekiwania na obu badanych przejściach granicznych jest taki sam

H1: czas oczekiwania na obu badanych przejściach granicznych statystycznie istotnie różni się od siebie

PROCEDURA POSTĘPOWANIA

1. Zbudować niemalejący szereg dla każdej próby. Tworzymy łączny szereg niemalejący.

Przejście A:

1 2 2 3 3 3 4 5 5 6 6 6

Przejście B:

3 4 4 5 5 6 7 7 8 8 8 9

Przejście A + B

1 2 2 3 3 3 3 4 4 4 5 5

5 5 5 5 5 5 7 7 8 8 8 9

Mamy 24 obserwacje.

2. Wyznaczamy wspólną medianę.

Mediana jest pomiędzy 12, a 13 obserwacją.

Me = 5

3. Budujemy tablicę czteropolową dla mediany.

	A	B	Σ
xi > Me	3 ^a	7 ^b	10
xi ≤ Me	9 ^c	5 ^d	14
Σ	12	12	24

4. Wyznaczamy wartość statystyki
   

Korzystamy z zmodyfikowanego wzoru, gdyż
mamy wzór









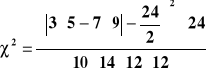
5. Porównuję z obszarem krytycznym



























χ² = 1,5


Interpretacja:

Nie ma podstaw do odrzucenia hipotezy H₀, która mówi o tym, że czas oczekiwania na obu badanych przejściach granicznych jest taki sam.

Zadanie 5

Wylosowano po 12 pędów żyta trzech różnych gatunków i otrzymano dla nich następujące długości kłosów żyta (w cm):

Gatunek A:

6,7 7,3 8,0 8,0 7,9 9,2 10,1 9,2 8,3 8,4 8,0 7,9

Gatunek B:

7,5 7,7 7,7 8,2 8,9 8,9 10,6 10,2 9,4 9,4 8,2 7,8

Gatunek C:

5,9 6,9 7,0 7,0 9,5 9,6 9,6 10,3 8,1 8,5 8,6 8,8

Za pomocą testu sumy rang zweryfikować na poziomie istotności α = 0,05 hipotezę, że długość kłosów jest jednakowa dla tych trzech gatunków żyta.

Test Kruskala-Wallisa (test sumy rang)

H0: wszystkie k populacje mają jednakowe rozkłady		Ho:F1(X)=F2(X)=…=Fk(X)
H1: nie wszystkie k populacje mają jednakowe rozkłady

H0: długości kłosów dla tych trzech gatunków są takie same

H1: przynajmniej jedna długość kłosa odbiega od innych

1. Nadajemy rangi. Sumujemy rangi dla każdego gatunku A, B, C.

A	rangi		B	Rangi		C	rangi
6,7	2		7,5	7		5,9	1
7,3	6		7,7	8,5		6,9	3
8,0	14		7,7	8,5		7,0	4,5
8,0	14		8,2	17,5		7,0	4,5
7,9	11,5		8,9	24,5		9,5	30
9,2	26,5		8,9	24,5		9,6	31,5
10,1	33		10,6	36		9,6	31,5
9,2	26,5		10,2	34		10,3	35
8,3	19		9,4	28,5		8,1	16
8,4	20		9,4	28,5		8,5	21
8,0	14		8,2	17,5		8,6	22
7,9	11,5		7,8	10		8,8	23
	198			245			223

Mamy 36 obserwacji.

2. Obliczamy statystykę
   









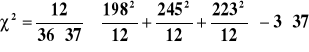
3. Porównuję z wartością krytyczną.



k - liczba gatunków
























χ² = 0,8303


Interpretacja:


Nie ma podstaw do odrzucenia H₀, która mówi, że długości kłosów dla tych trzech gatunków są takie same.

Zadania dotyczące testowania hipotez nieparametrycznych

4

(1) (2) (3) (4) (5) (6)

(6) (7) (8) (9) (10) (11)

k_α = 8 k = 11

---