Politechnika Śląska

Wydział chemiczny

Kier. Inżynieria chemiczna i procesowa

grupa II

TEMAT :

WYZNACZENIE STAŁEJ VERDETA

Wstęp teoretyczny:

Światło jest falą elektromagnetyczną. Jak każda fala przenosi energię z jednego miejsca do drugiego bez transportu materii. Ze względu, że światło jest częścią promieniowania elektromagnetycznego (czyli rozchodzących się w przestrzeni na przemian zmienne pole magnetyczne i elektryczne) może ulec polaryzacji. Ma to miejsce gdy jakiś czynnik zmusi chaotyczne drgania do tego, by odbywały się w jednej płaszczyźnie lub jakiegoś innego obranego porządku.

Najczęstszym przypadkiem jest polaryzacja liniowa, która ma miejsce gdy drgania wektora natężenia pola elektrycznego zachodzą tylko w jednej płaszczyźnie, która nie zmienia w czasie swej orientacji. W pewnych przypadkach wektor natężenia pola elektrycznego porusza się po linii kołowej i wtedy mówimy o polaryzacji kołowej.

Polaryzacja światła polega na tym, że trzeba podstawić coś co spowoduje, że światło przejdzie w jednym kierunku. Jest kilka metod polaryzacji światła:

• Za pomocą polaroidów:

• Przez odbicie (od dielektryków np. szkło)

Michaela Faradaya w 1846 roku odkrył, że niektóre ciała po umieszczeniu w polu magnetycznym skręcają płaszczyznę polaryzacji, chociaż w nieobecności pola magnetycznego były nieaktywne optycznie. Faraday ustalił, że kąt skręcenia płaszczyzny polaryzacji jest proporcjonalny do wartości indukcji pola magnetycznego B i do długości drogi l światła przechodzącego przez badaną substancję.

α=ωBl

gdzie: α-kąt skręcenia płaszczyzny, l-droga przebyta przez światło, B- indukcja magnetyczna ω-stała Verdeta (zależy od rodzaju substancji i długości fali)

Przebieg ćwiczenia:

Układ pomiarowy:

Do pomiaru skręcania płaszczyzny polaryzacji stosuje się polarymetry, których podstawowymi częściami są: źródło światła (np. lampa sodowa), dwa filtry polaryzacyjne (polaryzator i analizator), rurka, w której umieszcza się substancje aktywną optycznie oraz lunetka zapewniająca ostrość widzenia. Niezbędnym elementem przyrządu jest skala umożliwiająca odczytanie kata skręcania analizatora względem polaryzatora.

Substancją czynna optycznie jest nasycony roztwór jodku potasu. Umieszczony jest on w dużej cewce, przez którą płynie prąd o zadanym natężeniu. Indukcja magnetyczna wewnątrz solenoidu określona jest wzorem:

B=µ₀bNi

Gdzie: i-prąd płynący przez cewkę,

µ_0-przenikalność magnetyczna próżni (µ₀=4Π∙10^-7H/m)

N- liczba zwojów na jednostkę długości cewki (N=60 m^-1)

b- stała aparaturowa obliczona metodą całkowania graficznego przy uwzględnieniu rozmiarów cewki, liczby warstw uzwojenia i grubości drutu nawojowego (b=116)

Kolejność czynność przy wykonywaniu ćwiczenia:

Pierwszym krokiem było połączenie obwodu cewki. Następnie zmieniając natężenie prądu płynącego przez cewkę w zakresie od 7A do 0 A w dół co 1A i od -7A do 0A wzwyż co 1A zmierzono kąt skręcania płaszczyzny polaryzacji, który został odczytany za pomocą lupy w okularze. Aby pomiary były właściwe trzeba było ustawić analizator tak aby powstało

równe oświetlenie. Gdy płaszczyzna polaryzacji zmieniła się przy zmianie natężenia, tak że jedna z połówek pola widzenia stała się jaśniejsza a druga ciemniejsza, należało wyrównać tę różnicę obracając analizator o taki kąt, aby ponownie wyrównało się oświetlenie. Pomiaru dokonano trzykrotnie i w sumie otrzymano trzy serie po 15 pomiarów.

Opracowanie wyników:

1. Uśrednione kąty skręcania płaszczyzny polaryzacji dla danej wartości natężenia prądu obliczono ze wzoru:

gdzie: α_i-wartość kąta w serii

n- ilość serii, n=3

2. Niepewność całkowita średniego kąta z uwzględnieniem niepewności średniej krótkiej serii, jak i dokładność skali. Obliczono ze wzoru:

1. Niepewność krótkiej serii
   
   
   
   

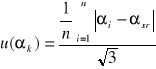
2. Niepewność całkowita średniego kąta
   
   
   
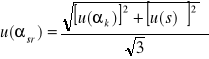
   gdzie: u(s)=0,05-dokładność skali

Wyniki z punktów 1 i 2 przedstawiono w tabeli 1.

Tabela 1

Lp.	I [A]	φ[°]			αsr	u(αk)	u(αsr)
				1				2	3
1	7,00	5°90'	5°95'	5°90'	5°92'	0,010	0,050
2	6,00	5°	5°10'	5°30'	5°13'	0,060	0,080
3	5,00	4°50'	4°40'	4°40'	4°43'	0,020	0,050
4	4,00	4°60'	4°70'	4°85'	4°72'	0,050	0,070
5	3,00	3°80'	3°90'	3°50'	3°87'	0,020	0,050
6	2,00	2°30'	2°15'	2°	2°15'	0,060	0,080
7	1,00	1°50'	1°40'	1°40'	1°43'	0,020	0,050
8	0	0°70'	0°65'	0°65'	0°67'	0,010	0,050
9	-1,00	0°	0°	0°	0°	0	0,050
10	-2,00	-0°70'	-0°95'	-1°	-0°88'	0,21	0,22
11	-3,00	-1°60'	-1°60'	-1°60'	-1°60'	0	0,05
12	-4,00	-2°50'	-2°25'	-2°35'	-2°37'	0,16	0,17
13	-5,00	-3°30'	-3°05'	-3°15'	-3°32'	0,27	0,28
14	-6,00	-4°	-3°80'	-4°	-3°93'	0,16	0,17
15	-7,00	-4°50'	-4°60'	-4°47'	-4°40'	0,10	0,050

3. Sporządzając wykres zależności wartości średniej kąta skręcenia płaszczyzny polaryzacji od natężenia prądu posłużono się programem Excel pakietu Microsoft Office.

4. Słupki niepewności dla natężenia prądu oraz średniej wartości kątów skręcenia wykonano w programie Excel pakietu Microsoft Orfice

u(s)=0,05

5. Metodą regresji liniowej dopasowano prostą do punktów pomiarowych. Wykonano to w programie Excel pakietu Microsoft Office.

6. Wyznaczanie stałej Verdeta:
   

gdzie:
ω-stała Verdeta,
l=0,2m-długość kuwety z cieczą
µ₀-przenikalność magnetyczna w próżni,
n=60m^-1-liczba zwojów
b=116-stała aparaturowa obliczona metodą całkowania graficznego przy uwzględnieniu rozmiarów cewki. Liczba warstw uzwojenia i grubości drutu nawojowego,

k-współczynnik proporcjonalności obliczony metoda regresji liniowej.

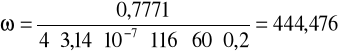
7. Niepewność stałej Verdeta obliczono wykorzystując S_a (bład wyznaczenia współczynnika obliczony metoda regresji liniowej):

Wnioski:

Ćwiczenie miało na celu pokazać jak zachowuje się światło spolaryzowane przy przejściu przez wodny roztwór jodku potasu o stężeniu bliskim nasyceniu.

Uzyskane dane posłużyły do wykreślenia zależność kąta skręcania płaszczyzny polaryzacji od natężenia prądu płynącego w solenoidzie. Zależność ma charakter linowy. Metodą regresji liniowej dopasowano prostą o równaniu y=0,7771x+0,7878 do punktów pomiarowych.

W wyniku obliczeń otrzymano wartość stałej Verdeta, która ostatecznie wyniosła:

Wyliczona wartość różni się od tablicowej, która wynosi:

Różnica wynika z rozkładu jodku potasu, który spowodował zmniejszenie stężenia roztworu.

---