V. TEORIE BUDOWY ATOMU

V.1. Miejsce i rola teorii w nauce

Na przełomie XIX i XX wieku okazało się, że ani zasady mechaniki klasycznej (sformułowane w połowie XVII przez Newtona), ani podane w 1862 przez Maxwella prawa elektrodynamiki nie tłumaczą szeregu zjawisk fizycznych takich, jak:

a) promieniowanie ciała doskonale czarnego,

b) efekt fotoelektryczny,

c) widma emisyjne atomów,

d) promieniotwórczość uranu i toru oraz ich związków,

a następnie

e) efekt Comptona odkryty w 1923 roku,

f) dyfrakcja strumienia elektronów na cienkich foliach metalicznych i kryształach odkryta w 1927roku..

Wyjaśnienie natury tych zjawisk i procesów stało się możliwe dopiero dzięki rozwojowi teorii kwantów, teorii dualizmu korpuskularno - falowego promieniowania elektromagnetycznego, pierwszym, podbudowanym teoretycznie modelom budowy atomu, sformułowaniu hipotezy de Broglie'a i równania Schrödingera, które zapoczątkowały burzliwy rozwój podstaw mechaniki kwantowej.

V.2.Wpływ wyników doświadczalnych na rozwój teorii
budowy atomu

V.2.1. Promieniowanie ciała doskonale czarnego

Ciało doskonale czarne, zwane również promiennikiem zupełnym, to wyidealizowany obiekt, który ma zdolność całkowitej absorpcji każdego padającego nań promieniowania.

Spośród ciał występujących w naturze, jedynie sadza wykazuje właściwości zbliżone do ciała doskonale czarnego. Z tego powodu w praktyce posługujemy się modelami ciała doskonale czarnego. Jeden z takich modeli ciała doskonale czarnego pokazano na rys. 1.

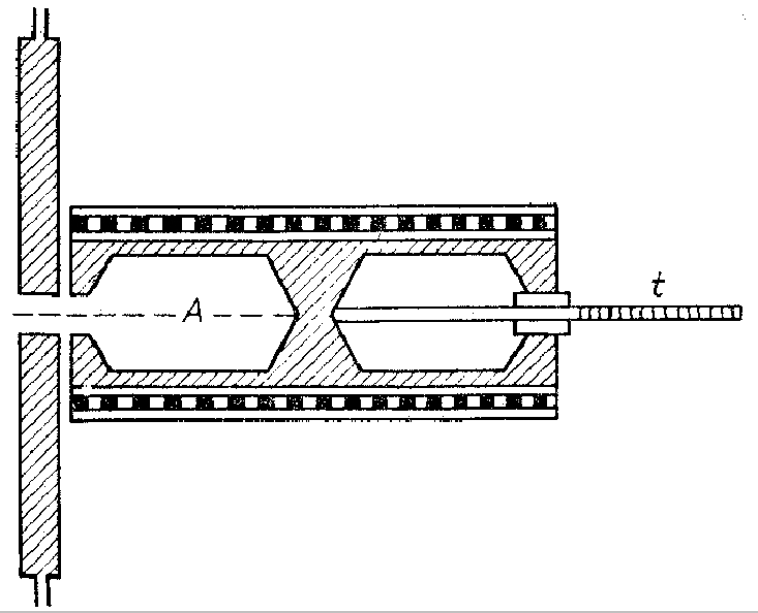
Rys. 1. Model ciała doskonale czarnego

Promieniowanie wpadające przez wąski otwór do pustej przestrzeni A ulega absorpcji po wielokrotnym odbiciu od ścianek. Przed otworem wlotowym znajduje się chłodzona przesłona, a w drugiej pustej przestrzeni urządzenie do pomiaru temperatury (termopara). Ogrzewanie całego układu prądem elektrycznym powoduje emisję promieniowania z przestrzeni A.

Jeśli ciało doskonale czarne pozostaje w równowadze termodynamicznej z promieniowaniem, to tym samym emituje dokładnie tyle samo energii promienistej, ile jej absorbuje. Rozkład intensywności (I) promieniowania ciała doskonale czarnego zależy od częstości ν
i temperatury. W określonej temperaturze krzywa I(ν) = f(ν) lub I(λ) = f(λ) przechodzi przez maksimum.

Ze wzrostem temperatury maksimum to przesuwa się w kierunku wyższych częstości (rys.2).

Rys. 2. Zależność I(λ) = f(λ) promieniowania emitowanego przez ciało doskonale czarnego

Pełną interpretację widma promieniowania ciała doskonale czarnego, zgodną z doświadczeniem, podał Max Planck, który w 1900 r. postulował, podobno
z najwyższą niechęcią (!), że materia nie może emitować energii inaczej, niż w określonych porcjach (ΔE) proporcjonalnych do częstości ν drgań punktów materialnych w ciele doskonale czarnym:

ΔE = hν,

Współczynnik h, równy 6,62607·10^-34 J·s, nosi miano stałej Plancka.

V.2.2. Efekt fotoelektryczny

Efekt fotoelektryczny, odkryty w 1888 roku, polega na wybijaniu przez promieniowanie ultrafioletowe elektronów z powierzchni metali. Z czystych powierzchni metali alkalicznych (np. potas, rubid, cez) elektrony wyzwalane są już pod wpływem promieniowania
w zakresie widzialnym, co znalazło zastosowanie do konstrukcji fotokomórek. Jest to tzw. zewnętrzny efekt fotoelektryczny, którym rządzą następujące prawa podane przez Lenarda:

• liczba wyzwalanych elektronów jest proporcjonalna do natężenia padającego promieniowania;

- maksymalna prędkość emitowanych elektronów zależy od częstości promieniowania, nie zależy natomiast od jego natężenia.

Wyjaśnienie tych praw podał Albert Einstein (1905), który założył, że pole elektromagnetyczne ma „strukturę nieciągłą”, bowiem składa się z porcji energii promienistej, nazwanych kwantami promieniowania lub po prostu fotonami.

Foton padając na warstwę metalu zderza się z jednym
z elektronów i przekazuje mu swoją energię, równą
z założenia hν. Część tej energii zostaje zużytkowana na pracę (W) potrzebną do uwolnienia elektronu
z powierzchni metalu, czyli tzw. pracę wyjścia, natomiast pozostała część energii fotonu zostaje przekazana wybitemu elektronowi jako energia kinetyczna. Zatem, zgodnie z prawem zachowania energii mamy:

gdzie m_e jest masą spoczynkową elektronu, a v jego prędkością po wybiciu.

W zjawisku fotoelektrycznym fotony promieniowania elektromagnetycznego wyraźnie przejawiają charakter korpuskularny, a hipoteza Einsteina ilościowo wyjaśnia oba prawa Lenarda. Pełne potwierdzenie tej hipotezy nastąpiło w 1923 roku, po wyjaśnieniu efektu Comptona.

V.2.3. Efekt Comptona

Compton obserwując zjawisko rozpraszania promieniowania rentgenowskiego przez węglowodory alifatyczne (alkany) stwierdził, że promieniowanie rozproszone zawiera składową o takiej samej długości fali λ jak promieniowanie pierwotne, a także składową o większej długości fali, λ' > λ. Compton i Debye założyli, że istota tego zjawiska (znanego jako efekt Comptona) polega na zderzeniu sprężystym fotonu z elektronem, zachodzącym zgodnie z prawami zachowania energii i wypadkowego pędu, co pokazano na rys. 3.

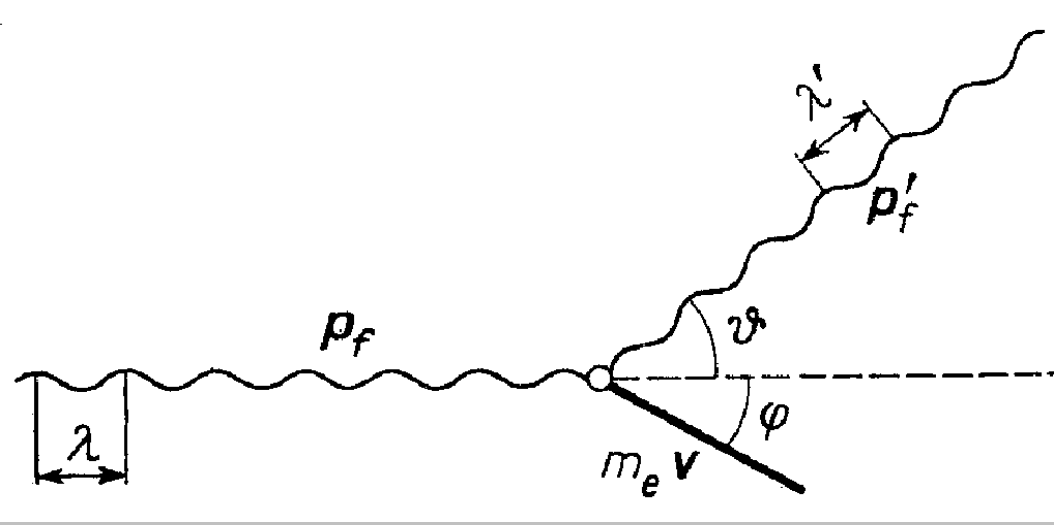
Rys. 3. Efekt Comptona

Aby zadość uczynić prawu zachowania wypadkowego pędu należało określić pęd fotonu p_f. Ponieważ dla fotonu mamy:

to

gdzie m_f i c oznaczają odpowiednio masę fotonu i prędkość światła. Oczywiście wektor pędu fotonu ma kierunek
i zwrot zgodne z kierunkiem i zwrotem rozchodzenia się czoła fali elektromagnetycznej.

Efekt Comptona potwierdza zatem fakt, że promieniowanie elektromagnetyczne należy traktować jako zbiór fotonów o określonej energii, hν, i pędzie h/λ. Innymi słowy, w efektach fotoelektrycznym i Comptona przejawia się dualizm korpuskularno - falowy promienio-wania elektromagnetycznego.

V.2.4. Promienie katodowe i kanalikowe

Rozrzedzone gazy umieszczone w rurkach szklanych zaopatrzonych w elektrody świecą po wpływem przyłożonego napięcia. Przy bardzo niskich ciśnieniach (p < 100 Pa) efekty świetlne w gazie wypełniającym rurkę zanikają, a na ściankach naprzeciw katody obserwuje się fosforescencję szkła pod wpływem niewidzialnego promieniowania emitowanego przez katodę w kierunku prostopadłym do jej powierzchni. Okazało się, że promieniowanie katodowe jest strumieniem elektronów odpowiedzialnym za przewodnictwo rozrzedzonych gazów wypełniających rurkę.

Jeśli w katodzie znajdują się wąskie kanaliki, to w rurce wypełnionej rozrzedzonym gazem pojawia się inne promieniowanie, które nazwano promieniowaniem kanalikowym. Promieniowanie to jest strumieniem
dodatnio zjonizowanych atomów gazu wypełniającego rurkę, poruszającym się w przeciwnym kierunku niż promieniowanie katodowe.

Rys. 4. Promienie katodowe i kanalikowe w rurce Geisslera

W 1904 roku Thomson, kierując się wnioskami
z doświadczeń z promieniowaniem katodowym
i kanalikowymi, zaproponował model atomu znany jako
„ciastko z rodzynkami”. Thomson założył, że każdy atom jest zbudowany z jednorodnej kuli naładowanej dodatnio, wewnątrz której znajdują się ujemnie naładowane elektrony.

.

Rys. 5. Model atomu według Thomsona

V.2.5. Promieniotwórczość naturalna

W 1896 roku Becquerel odkrył promietwórczość rudy uranowej emitującej samorzutnie promieniowanie, które powoduje jonizację powietrza, zaczernienie kliszy fotograficznej nawet bez dostępu światła, fluorescencję niektórych substancji, itp. Warunki zewnętrzne nie mają wpływu na to promieniowanie i nie można go w żaden sposób osłabić lub wzmocnić. W polu elektrycznym lub magnetycznym promieniowanie to ulega rozszczepieniu na trzy składowe. Promieniowanie α jest strumieniem cząstek o masie 4 jednostek u i ładunku +2, odchylającym się
w stronę ujemnej okładki kondensatora. Cząstki promieniowania α są identyczne z dwukrotnie zjonizowanymi atomami izotopu helu o liczbie masowej 4. Promieniowanie β jest strumieniem elektronów odchylającym się w kierunku dodatniej okładki kondensatora. Promieniowanie γ jest promieniowaniem elektromagnetycznym o długości fali około 10000 razy krótszej niż światło widzialne, identycznym
z odkrytymi niemal równocześnie promieniami Röntgena .

Promieniowanie α odegrało zasadniczą rolę
w słynnym doświadczeniu Rutherforda, który rejestrował tory cząstek α padających na bardzo cienką folię ze złota. Zdecydowana większość tych cząstek przenikała przez folię bez zmiany kierunku, tory bardzo niewielkiej liczby cząstek odchylały się od pierwotnego kierunku, a tylko pojedyncze cząstki praktycznie odbijały się od folii. Obserwację zmian torów cząstek α umożliwił Rutherfordowi ekran powleczony siarczkiem cynku. Ideę doświadczenia Rutherforda ilustruje rys. 6.

Rys.6. Schemat doświadczenia Rutherforda

Z przeprowadzonego doświadczenia Rutherford wyciągnął daleko idące wnioski obalające model atomu Thomsona:

- cząstka α odbija się od folii tylko w wyniku zderzenia
z ładunkami dodatnimi w atomie materiału folii;

- odbicie cząstek α od folii zdarza się bardzo rzadko, ponieważ ładunki dodatnie w atomie skupione są
w bardzo małej objętości w stosunku do objętości atomu, a ich masa jest praktycznie równa masie atomu, co wcześniej zostało potwierdzone w badaniach natury promieni kanalikowych.

Według Rutherforda (rok 1911) masa atomu jest skoncentrowana w jądrze atomowym, a reszta przestrzeni zajmowanej przez atom wypełniona jest przez elektrony, które jednak nie wypełniają jej w sposób tak gęsty, aby mogły zahamować bieg cząstek α lub zmienić tor ich ruchu.

V.2.6. Widma emisyjne atomów i jonów. Postulaty Bohra dotyczące atomu wodoru

W wysokich temperaturach atomy lub zjonizowane atomy pierwiastków znajdujących się w fazie gazowej emitują promieniowanie elektromagnetyczne, którego widmo jest liniowe. W przypadku promieniowania emitowanego przez atomy wodoru wykryto kilka serii widmowych, przy czym jedna z nich, zwana serią Balmera, pojawia się w zakresie widzialnym (rys. 7).

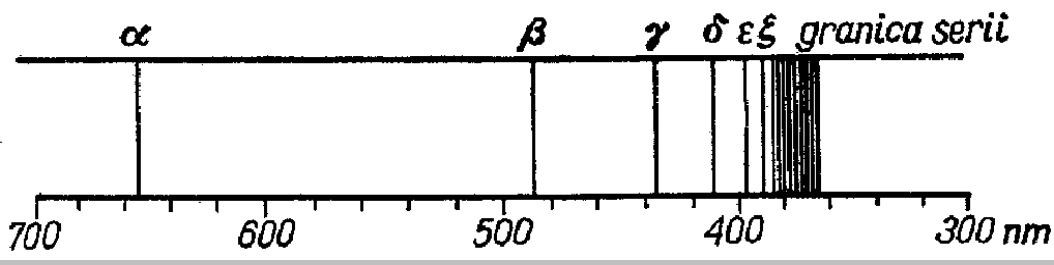
Rys. 7. Seria Balmera w widmie emisyjnym wodoru

Długości fal promieniowania w serii Balmera spełniają empiryczną zależność:

gdzie n jest liczbą naturalną większą od 2, a R_H jest stałą Rydberga równą 109667 cm^-1.

Teoretyczne wyjaśnienie serii obserwowanych w widmie emisyjnym wodoru podał w 1913 roku Niels Bohr, który sformułował dwa następujące postulaty:

1. Dla elektronów poruszających się w atomie względem jądra dopuszczalne są tylko tzw. tory stacjonarne. Elektron znajdujący się na takim torze nie emituje promieniowania,
   a jego moment pędu podlega kwantowaniu, ponieważ jest równy nh/2π, gdzie n jest liczną naturalną, równą numerowi kolejnego toru stacjonarnego (licząc od najbliższego toru względem jądra, któremu odpowiada n = 1). Energia całkowita elektronu również jest kwantowana, ponieważ jest proporcjonalna do 1/n².

2. Przejście elektronu z jednego toru stacjonarnego (n₁) na inny tor stacjonarny (n₂) wiąże się z absorpcją (gdy n₁ < n₂) lub emisją (gdy n₁ > n₂) kwantu promieniowania o energii hν = ΔE, gdzie ΔE jest wartością bezwzględną różnicy energii elektronu na odpowiednich torach stacjonarnych.

Postulaty Bohra mają fundamentalne znaczenie dla planetarnego modelu atomu. Obydwa postulaty pozwoliły Bohrowi podać pełną i zgodną
z doświadczeniem, interpretację poszczególnych serii obserwowanych w widmie emisyjnym wodoru. Schemat przejść elektronowych dla poszczególnych serii w tym widmie pokazano na rys. 8.

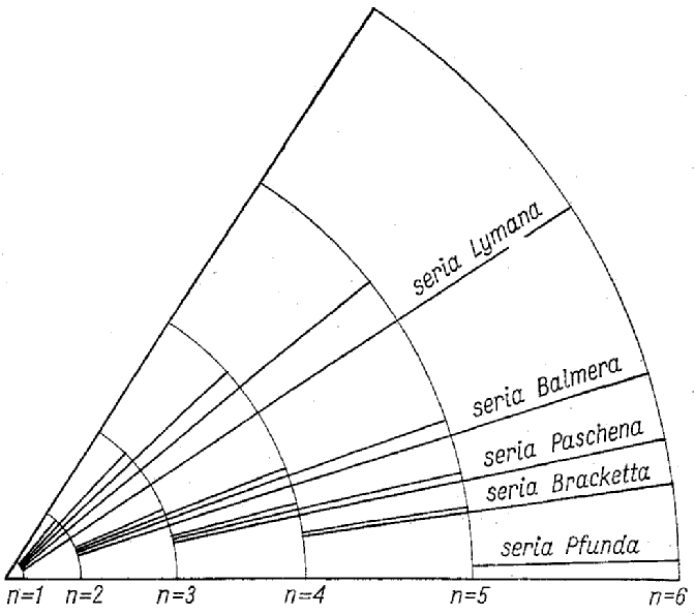
Rys. 8. Serie obserwowane w widmie emisyjnym wodoru

Niestety, model Bohra zawodzi w przypadku atomów cięższych pierwiastków.

V.3. Hipoteza de Broglie'a

Dualizm korpuskularno-falowy przejawiają również strumienie rozpędzonych cząstek, np. elektronów, protonów, neutronów, oraz cząstek α. Zgodnie z hipotezą de Broglie'a (1923) cząstkom o pędzie p przypisuje się falę o długości λ:

Dowodem na to jest wykryta w 1927 roku przez Davissona i Germera dyfrakcja strumienia elektronów na cienkich foliach metalicznych
i kryształach. Również strumienie protonów, neutronów i cząstek α ulegają dyfrakcji na kryształach.

Należy podkreślić, że konsekwencje hipotezy de Broglie'a miały fundamentalne znaczenie w opisie zachowania się elektronów w atomie. Na jej podstawie Erwin Schrödinger w 1926 sformułował zasady mechaniki kwantowej i dla cząstki poruszającej się w dowolnym polu potencjalnym wyprowadził równanie, które pozwala znaleźć odpowiednią funkcję falową.

---