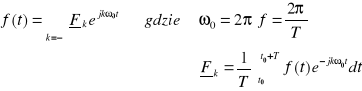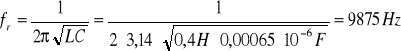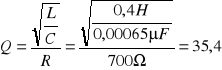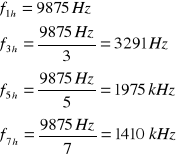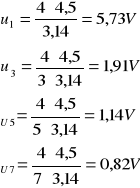Temat: Zjawisko rezonansu napięć w obwodzie RLC przy wymuszeniu sinusoidalnym i prostokątnym |
Ocena: 4 pkt/4 |
Cel ćwiczenia:
Celem ćwiczenia jest zapoznanie się ze zjawiskiem rezonansu napięć w obwodzie szeregowym RLC przy wymuszeniu sinusoidalnym i prostokątnym. W ćwiczeniu należy zaobserwować charakterystyki częstotliwościowe przy wymuszeniu sinusoidalnym i prostokątnym, określić dobroć układu rezonansowego, zapoznać się ze zjawiskiem rezonansu dla wielu harmonicznych.
Podstawy teoretyczne:
|
Rezonansem w obwodzie elektrycznym nazywamy taki stan, że pomimo istnienia cewek i kondensatorów impedancja tego obwodu ma charakter rezystancyjny. W stanie tym napięcie i prąd wejściowy są zgodne w fazie a w obwodzie następuje kompensacja mocy i układ nie pobiera mocy biernej. Zjawisko rezonansu występuje tylko przy ściśle określonej częstotliwości sygnału zasilającego obwód. Częstotliwość tą nazywamy częstotliwością rezonansową.
Rezonans jest charakteryzowany przez różne parametry, którymi mogą być częstotliwość rezonansowa, dobroć obwodu rezonansowego, rezystancja charakterystyczna i pasmo przenoszenia częstotliwości.
Dla dwójnika szeregowego RLC można napisać następujące napięciowe równanie Kirchhoffa:
![]()
Warunkiem rezonansu jest zgodność w fazie prądu i napięcia wejściowego. Jest to osiągane gdy XL = XC. Wiedząc, że XL = ωL oraz XC = 1/ωC otrzymujemy wzór na pulsację rezonansową ωr postaci ![]()
. Stąd częstotliwość rezonansowa będzie się wyrażała zależnością:
![]()
Widać z tego, że częstotliwość rezonansowa zależy od indukcyjności L i pojemności C, natomiast rezystancja R nie ma na nią wpływu.
![]()
Drugim ważnym parametrem obwodu rezonansowego jest dobroć Q, która jest definiowana jako stosunek napięcia na elemencie reaktancyjnym do napięcia na elemencie rezystancyjnym podczas rezonansu. Zależność tą można zapisać wzorem:
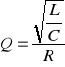
Dobroć obwodu mówi nam o przepięciu w obwodzie podczas rezonansu, ponieważ wskazuje ile razy napięcie na elemencie reaktancyjnym jest większe od napięcia na zaciskach obwodu. Zależność powyższą można uzależnić jedynie od parametrów obwodu do postaci:
Wielkość występująca w liczniku jest nazywana rezystancją charakterystyczną ρ i zależy tylko od wartości indukcyjności i pojemności.
Zależność prądu i napięć od częstotliwości nazywamy charakterystykami częstotliwościowymi obwodu rezonansowego. Zależność modułu od częstotliwości jest to charakterystyka amplitudowa, a zależność fazy od częstotliwości to charakterystyka fazowa. Te dwie zależności dla prądu opisane są następująco:
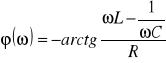
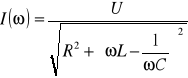
Dla rezonansu amplituda przyjmuje wartość maksymalną a faza wartość zerową.
Wykorzystując prawo Ohma możemy uzyskać charakterystyki amplitudowe i fazowe dla pozostałych elementów obwodu RLC:
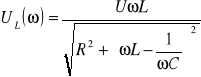
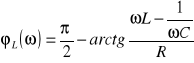
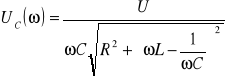
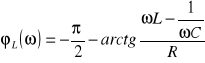
Dla częstotliwości rezonansowej napięcia na elementach reaktancyjnych są sobie równe. Charakterystyki fazowe na cewce i kondensatorze natomiast od charakterystyki fazowej prądu różnią się tylko o wartość π/2 i są przesunięte na osi pionowej w górę lub w dół.
Duży wpływ na charakterystyki częstotliwościowe ma dobroć obwodu. Im dobroć jest większa, tym charakterystyka dla częstotliwości rezonansowej jest bardziej stroma i węższa (lepsza selektywność obwodu rezonansowego).
Pasmem przenoszenia obwodu rezonansowego RLC nazywamy przedział częstotliwości, na krańcach którego wartość skuteczna napięcia na rezystorze jest równa U/√2 ( spadek wartości charakterystyki logarytmicznej o 3 dB w stosunku do wartości maksymalnej). Jest ono opisane następującą zależnością:
![]()
|
WSTĘP:
Klasyfikując sygnały elektryczne mówimy, że wszystkie sygnały okresowe tętniące i przemienne, nie mające charakteru sinusoidalnego zaliczamy do klasy sygnałów niesinusoidalnych lub odkształconych.
Funkcja okresowa niesinusoidalna f(t) (spełniająca warunki Dirchleta) może być wyrażona za pomocą nieskończonego zbieżnego szeregu Fouriera. Suma tego szeregu jest równa funkcji f(t) gdzie:
Postać wykładnicza |
|
Postać trygonometryczna |
|
Wykres Fk określony dla dyskretnych wartości k reprezentujących sobą dyskretne częstotliwości nazywamy widmem amplitudowym funkcji f(t) - jest ono symetryczne względem osi rzędnych. Z kolei wykres argumentów funkcji f(t) jest nazywane widmem fazowym - jest ono symetryczne względem początku układu współrzędnych.
Prążki amplitudowe i fazowe występują jedynie dla wartości dyskretnych częstotliwości będących wielokrotnościami częstotliwości podstawowej ωo. Są one rozłożone w sposób symetryczny w obu zakresach częstotliwości dodatnich i ujemnych, przy czym charakterystyka amplitudowa jest funkcją parzystą a fazowa nieparzystą. Amplituda k-tej harmonicznej jest równa podwojonej wartości amplitudy k-tego prążka z zakresu dodatniego i ujemnego.
REZONANS przy wymuszeniu prostokątnym:
Dla obwodu RLC który jest zasilany napięciem prostokątnym jednopolarnym o wypełnieniu 1:1 zasilanie obwodu można przedstawić jako superpozycję wielu napięć harmonicznych o częstotliwościach będących wielokrotnością częstotliwości podstawowej i amplitudach malejących wraz z rzędem. Jako, że reaktancje cewki i kondensatora są zależne od częstotliwości przebiegu zatem impedancja obwodu dla k-tej harmonicznej określona jest wzorem:
![]()
![]()
Przy czym częstotliwość zasilania ωok przy której występuje rezonans dla k-tej harmonicznej jest określana następująco: .
Charakterystyki częstotliwościowe dla każdej harmonicznej są identyczne jak dla przebiegów sinusoidalnych tyle, że różnią się częstotliwością rezonansową i dobrocią.
Oto przykładowe charakterystyki:
Dla przebiegu prostokątnego częstotliwości równej częstotliwości drgań własnych obwodu RLC dominuje harmoniczna podstawowa prądu. Przy zmniejszaniu częstotliwości coraz większy wpływ mają wyższe harmoniczne (przebieg prądu odkształcony). Dla częstotliwości większej niż f0 zjawisko rezonansów wyższych harmonicznych nie występuje. W odróżnieniu od prądu w charakterystyce napięcia na kondensatorze należy wyodrębnić składową stałą.
3. Przebieg ćwiczenia
Pomiary wykonaliśmy w układzie o poniższych parametrach:
L = 0,4 H C = 0,000650 µF R = 700 Ω Amplituda napięcia prostokątnego: Um=4,5V |
W ćwiczeniu wykorzystaliśmy programowalny generator, który generował liniowo zmienną częstotliwość w zakresie od 1kHz do 11 kHz. Naszym zadaniem było zaobserwować i zdjąć charakterystyki częstotliwościowe z każdego elementu (R, L i C) dla zasilania przebiegiem sinusoidalnym i prostokątnym.
3.1. Badanie zjawiska rezonansu przy wymuszeniu sinusoidalnym
Częstotliwość rezonansową wyliczyliśmy ze wzoru: |
Wartość odczytana z oscyloskopu wynosi: fr=~9 kHz |
Dobroć układu obliczyliśmy ze wzoru: |
|
Wartość dobroci wyznaczona z charakterystyki wynosi: |
|
Dla wymuszenia sinusoidalnego narysowaliśmy charakterystyki teoretyczne wartości skutecznej prądu i napięć na kondensatorze i cewce w funkcji częstotliwości.
3.2. Badanie zjawiska rezonansu przy wymuszeniu prostokątnym
Postać Fouriera podłączonego przebiegu prostokątnego: |
|
|
|
Częstotliwości harmonicznych występujących podczas zasilania układu sygnałem prostokątnym obliczyliśmy ze wzoru:
Wzór:
|
|
Wartości częstotliwości poszczególnych harmonicznych odczytane z wykresów wynoszą:
F3h=~3,05kHz
F5h=~1,75kHz
F7h=~1,3kHz
Wartości napięć maksymalnych poszczególnych harmonicznych: |
|
Wzór:
|
|
Dla wymuszenia prostokątnego narysowaliśmy charakterystyki teoretyczne wartości skutecznej prądu i napięć na kondensatorze i cewce w funkcji częstotliwości.
4. Wnioski
Obserwowane zjawisko rezonansu w obwodzie szeregowym RLC nastąpiło przy częstotliwości rezonansowej równej 9 kHz (wartość odczytana z oscyloskopu), lecz z naszych obliczeń wynika, że powinno ono występować przy częstotliwości wyższej a mianowicie 9,875 kHz. Jest to duża rozbieżność, która może być spowodowana niedokładnymi elementami obwodu, które mogą posiadać inne wartości parametrów od tych, które im zadaliśmy (szczególnie cewka).
Znając wartość napięcia na rezystorze widocznego na wykresie można obliczyć wartość prądu płynącego w obwodzie z prawa Ohma (I=U/R). Tak wyliczony prąd może posłużyć nam do sprawdzenia poprawności napięcia na cewce w rezonansie (znając częstotliwość): UL=I*XL=I*2Лf*L.
Wyliczona dobroć obwodu wyniosła 35,4 natomiast wyznaczając ją z otrzymanej charakterystyki amplitudowej otrzymaliśmy wynik 15, co stanowi mniej niż połowę wartości teoretycznej. Spowodowane to może być tym samym błędem co poprzednio oraz błędem w odczycie częstotliwości potrzebnych do obliczenia dobroci metodą graficzną.
Dla wymuszenia prostokątnego zaobserwowaliśmy zjawisko rezonansu dla wyższych harmonicznych. Częstotliwości rezonansowe wyższych harmonicznych odczytane z charakterystyki nieznacznie odbiegają od częstotliwości wyliczonych. Jednakże z całą pewnością możemy powiedzieć, że potwierdzają słuszność zjawisk jakie zachodzą w tych obwodach a w szczególności to, przebieg prostokątny składa się z wielu sinusoid nałożonych na siebie.
Należy jeszcze wyjaśnić dlaczego amplituda prążka podstawowego jest większa od tego pochodzącego od zwykłej sinusoidy. Jest to spowodowane obecnością w postaci dla sygnału prostokątnego członu 4/Л który warunkuje 27% wzrost amplitudy.
7
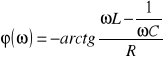
![]()
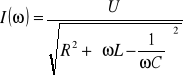
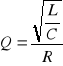
![]()
Wyszukiwarka
Podobne podstrony:
Badanie rezonansu w obwodach RLC, laboratorium podstaw elektroniki
cw4 rezonans elektryczny w obwodach RLC
cw4 rezonans elektryczny w obwodach RLC
07 Drgania w obwodach RLC
24 Badanie rezonansu w obwodach elektrycznych
Rezonans w obwodach elektrycznych v5(1), POLITECHNIKA LUBELSKA w LUBLINIE
Rezonans w obwodach elektrycznych v5(1), POLITECHNIKA LUBELSKA w LUBLINIE
stany nieustalone w obwodach RLC zasilanych ze źródła napięcia stałego, Politechnika Lubelska, Studi
drgania tlumione w obwodach RLC, ˙w
ćw.18, 31 Bernady, BADANIE REZONANSU W OBWODZIE RLC
Rezonans w obwodach prądu sinusoidalnego.DOC, ty
Rezonans w obwodach prądu sinusoidalnego , Nag³ówek
Sprawozdanie rezonans równoległy RLC
badanie rezonansu w obwodzie rlc
drgania tłumione w obwodach RLC, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Labora
Rezonans w obwodach elektrycznych v12, Elektrotechnika
Metro POMIARY MOCY CZYNNEJ I BIERNEJ ORAZ ENERGII W OBWODACH JEDNOFAZOWYCH, metrologia
Rezonans w obwodach elektrycznych v9, POLITECHNIKA LUBELSKA
więcej podobnych podstron