Nr ćwicz. 201 |
Data: 25.03.2013r |
Imię i Nazwisko
Oskar Grabowski |
Wydział Elektryczny |
Semestr II |
|
prowadzący mgr inż. Bartosz Bursa
|
Przygotowanie: |
Wykonanie: |
Ocena ostat. : |
||
Temat : Wyznaczanie zależności przewodnictwa od temperatury dla półprzewodników i przewodników .
Wstęp teoretyczny
Prawo Ohma stwierdza , że :
![]()
,
gdzie j - gęstość prądu ,
E - natężenie pola elektrycznego ,
- przewodnictwo elektryczne .
Przewodnictwo elektryczne określone jest wzorem :
![]()
n , p - koncentracje nośników ,
n , p - ruchliwość nośników .
Ponieważ koncentracja i ruchliwość zależą od temperatury i rodzaju materiału , więc przewodnictwo elektryczne także zależy od tych czynników .
O zależności temperaturowej przewodnictwa w metalach decyduje tylko zmniejszanie się ruchliwości wraz ze wzrostem temperatury ( koncentracja nośników - elektronów - jest bardzo duża i nie zależy od temperatury ) . Zależność temperaturową wyraża się poprzez opór (R1/ ) :
![]()
,
R0 - opór w temperaturze T0 ,
- średni współczynnik temperaturowy .
W półprzewodnikach decydujący wpływ na przewodnictwo ma koncentracja nośników. W przypadku półprzewodników samoistnych koncentracja elektronów i dziur jest taka sama i wynosi :
![]()
,
Eg - szerokość pasma zabronionego .
Natomiast w półprzewodnikach domieszkowych koncentracje określone są poprzez poziomy energetyczne (zależnie od typu półprzewodnika ) Ed - donorowy , Ea - akceptorowy , oraz poprzez temperaturę :
![]()
.
Uwzględniając powyższe równania otrzymujemy wzór na temperaturową zależność przewodnictwa dla półprzewodników :
![]()
,
Edom jest jedną z wielkości Ed lub Ea zależnie od typu półprzewodnika .
W odpowiednio niskich temperaturach można zaniedbać w powyższym wzorze pierwszy składnik , natomiast w wysokich temperaturach ( po nasyceniu poziomów domieszkowych ) można zaniedbać składnik drugi . Odpowiednio dla tych dwóch przypadków wzór przyjmie postać :
![]()
.
Logarytmując jeden z powyższych wzorów otrzymamy zależność :
` ![]()
Z wykresu tej zależności wygodnie jest odczytać zależność przewodnictwa od temperatury :
Zasada pomiaru
Pomiarów oporu półprzewodnika i przewodnika dokonuje się w różnych temperaturach . Badane materiały umieszczone są w ultratermostacie , a ich opory mierzy się przy pomocy mostka Wheatstone'a .
Pomiary
Tabela wartości pomiarów dla przewodnika
Lp. |
T |
R |
|
[oC] |
[] |
1 |
25,6 |
110,7 |
2 |
28 |
111,5 |
3 |
33 |
113,4 |
4 |
38 |
115,3 |
5 |
43 |
117,2 |
6 |
48 |
119,1 |
7 |
53 |
121 |
8 |
58 |
122,8 |
9 |
63 |
124,8 |
10 |
68 |
126,6 |
11 |
73 |
128,6 |
12 |
78 |
130,4 |
13 |
83 |
132,2 |
14 |
88 |
134,1 |
15 |
93 |
136 |
Tabela wartości pomiarów dla półprzewodnika
Lp. |
T |
R |
|
[oC] |
[K] |
1 |
25,6 |
185 |
2 |
28 |
159 |
3 |
33 |
129 |
4 |
38 |
106 |
5 |
43 |
88,4 |
6 |
48 |
71,6 |
7 |
53 |
59,9 |
8 |
58 |
50,4 |
9 |
63 |
42,2 |
10 |
68 |
35,7 |
11 |
73 |
30,6 |
12 |
78 |
25,7 |
13 |
83 |
22,2 |
14 |
88 |
19,1 |
15 |
93 |
16,6 |
Analiza pomiarów
Błąd pomiaru rezystancji mostkiem Wheatstone'a : R=0.1
Błąd pomiaru temperatury : T=0.5C
Wykres zależności R=f(T) dla przewodnika
Wykres zależności R=f(T) dla półprzewodnika
Tabela zależności T, R, z obliczonymi ln(1/R) oraz 1/T dla półprzewodnika:
Lp. |
T |
T |
R |
R |
ln(1/R) |
1/T |
|
[oC] |
[K] |
[K] |
[] |
|
[1/K] |
1 |
25,6 |
298,75 |
185 |
185000 |
-12,1281 |
0,003347 |
2 |
28 |
301,15 |
159 |
159000 |
-11,9767 |
0,003321 |
3 |
33 |
306,15 |
129 |
129000 |
-11,7676 |
0,003266 |
4 |
38 |
311,15 |
106 |
106000 |
-11,5712 |
0,003214 |
5 |
43 |
316,15 |
88,4 |
88400 |
-11,3896 |
0,003163 |
6 |
48 |
321,15 |
71,6 |
71600 |
-11,1789 |
0,003114 |
7 |
53 |
326,15 |
59,9 |
59900 |
-11,0004 |
0,003066 |
8 |
58 |
331,15 |
50,4 |
50400 |
-10,8277 |
0,00302 |
9 |
63 |
336,15 |
42,2 |
42200 |
-10,6502 |
0,002975 |
10 |
68 |
341,15 |
35,7 |
35700 |
-10,4829 |
0,002931 |
11 |
73 |
346,15 |
30,6 |
30600 |
-10,3288 |
0,002889 |
12 |
78 |
351,15 |
25,7 |
25700 |
-10,1542 |
0,002848 |
13 |
83 |
356,15 |
22,2 |
22200 |
-10,0078 |
0,002808 |
14 |
88 |
361,15 |
19,1 |
19100 |
-9,85744 |
0,002769 |
15 |
93 |
366,15 |
16,6 |
16600 |
-9,71716 |
0,002731 |
Przykładowe obliczenia:
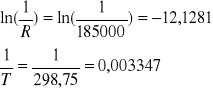
Wykres zależności ln(1/R) do 1/T:
Współczynnik nachylenia prostej ln(1/R)=f(1/T) obliczony metodą regresji wynosi :
a=-3869,1
Poziom domieszkowy będzie zatem równy :
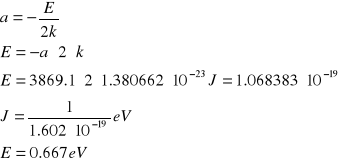
![]()
Wnioski:
W ćwiczeniu powyższym badana była zależność rezystancji od temperatury dla przewodnika i półprzewodnika. Badany przewodnik wykazywał dużą stabilność rezystancji przy zmianach temperatury, w porównaniu z półprzewodnikiem. Z przeprowadzonych pomiarów można zaobserwować że wzrost rezystancji przewodnika i wzrost temperatury związany jest ze zmniejszeniem się ruchliwości elektronów, a co za tym idzie zmniejszeniem się przewodności. W półprzewodniku zaobserwowaliśmy natomiast sytuację odwrotną do powyższej. Wartość rezystancji malała wraz ze wzrostem temperatury, jednocześnie powodując wzrost przewodności. Wzrost rezystancji przewodnika ma charakter liniowy, natomiast wzrost przewodności w półprzewodniku ma charakter wykładniczy.
Wyszukiwarka
Podobne podstrony:
SPOKO OBLICZENIA, Politechnika Poznanska, SEMESTR 2, laboratoria fizyka, 301
Super 201, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, Laborki, laborki fiza, Fiz
201 sprawozdanie-fizyka, Studia Politechnika Poznańska, Semestr II, I pracownia fizyczna, LABORKI WS
201-04, Studia Politechnika Poznańska, Semestr II, I pracownia fizyczna, LABORKI WSZYSTKIE, FIZYKA 2
201, Politechnika Poznańska ZiIP, II semestr, Fizyka, laborki fiza, 201
Destylacja wojtek, Studia Politechnika Poznańska, Semestr I, Chemia, Chemia laboratoria, Destylacja
103, Studia Politechnika Poznańska, Semestr II, I pracownia fizyczna, LABORKI WSZYSTKIE, FIZYKA 2, F
NASZE, Politechnika Poznanska, SEMESTR 2, TO laboratoria, cw 2 Twierdzenie Thevenina i Nortona
cw 6 Rezonans w obwodzie szeregowym, Politechnika Poznanska, SEMESTR 2, TO laboratoria
PROTOKÓŁ - analiza termiczna, Studia Politechnika Poznańska, Semestr I, Chemia, Chemia laboratoria,
potencjal wojtek, Studia Politechnika Poznańska, Semestr I, Chemia, Chemia laboratoria, Wyznaczanie
105A, Studia Politechnika Poznańska, Semestr II, I pracownia fizyczna, LABORKI WSZYSTKIE, FIZYKA 2,
Rozpad nuklidu, Studia Politechnika Poznańska, Semestr I, Chemia, Chemia laboratoria, Stała rozpadu
galwanotechnika, Studia Politechnika Poznańska, Semestr I, Chemia, Chemia laboratoria, Galwanotechni
302 abulec, Studia Politechnika Poznańska, Semestr II, I pracownia fizyczna, LABORKI WSZYSTKIE, FIZY
więcej podobnych podstron