Politechnika Śląska Gliwice 29.03.1999r.
Wydział Elektryczny
Kierunek EiT
Ćwiczenie laboratoryjne z fizyki
Pomiary indukcyjności i pojemności metodą techniczną.
Grupa T2 sekcja I
Tomasz Hauser
Paweł Łoskot
Wprowadzenie.
Zjawisko samoindukcji polega na wzbudzaniu prądu indukcyjnego w obwodzie, w którym następują zmiany natężenia prądu płynącego ze źródła. Zmiany natężenia prądu powodują zmiany indukcji magnetycznej, a te z kolei powodują zmiany strumienia magnetycznego. Na skutek zjawiska samoindukcji w obwodzie elektrycznym oprócz prądu płynącego ze źródła przez obwód przepływa prąd samoindukcji. Powstaje siła elektromotoryczna samoindukcji:
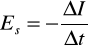
przeciwstawiająca się zmianom natężenia prądu pierwotnego płynącego ze źródła (reguła Lentza). L oznacza współczynnik samoindukcji (indukcyjność) przewodnika, ![]()
- szybkość zmian natężenia prądu. L zależy tu od długości przewodnika (znajdującego się w obwodzie) lub liczby zwojów oraz obecności ferromagnetycznego rdzenia.
Siła elektromotoryczna samoindukcji wywołuje pewien opór samoindukcji Rs, który wraz z oporem omowym R przewodnika stanowi właściwy opór w tym obwodzie. Opór łączny obwodu jest równy:
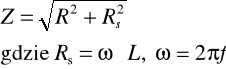
f - częstość zmian prądu na sekundę.
więc
![]()
Tak wygląda opór dla obwodu zawierającego przewodnik i cewkę.
W obwodzie zawierającym kondensator opór łączny jest równy:
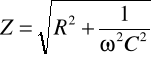
gdzie C jest pojemnością kondensatora.
W obwodzie prądu zmiennego zawierającym i cewkę i kondensator opór całkowity jest równy:
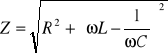
Natężenie prądu płynącego w tych obwodach zgodnie z prawem Ohma można zapisać wzorem:
![]()
Przebieg ćwiczenia.
Łączymy obwód według schematu na rysunku 1.
Mierzymy zmiany napięcia i prądu na cewce przy napięciu zasilającym zmieniającym się w granicach 0[V] - 2[V] co 0,2[V]. Wyniki zamieszczamy w tabeli nr. 1,
Łączymy obwód według schematu na rysunku 2.
Mierzymy zmiany napięcia i prądu na cewce z rdzeniem i bez rdzenia przy napięciu zasilającym zmieniającym się w granicach 0[V] - 6[V] co 0,5[V]. Wyniki zamieszczamy w tabeli nr. 2,3.
Łączymy obwód według schematu na rysunku 3.
Mierzymy zmiany napięcia i prądu dla kondensatorów C1 , C2 , C3 oraz dla ich połączenia szeregowego i równoległego, przy napięciu zasilającym zmieniającym się w granicach 0[V] - 6[V]. Wyniki zamieszczamy w tabeli nr. 4,5,6,7,8.
Spis przyrządów.
Woltomierz - Metex M-4650,
Amperomierz - Metex M-4650,
Zasilacz stabilizowany ZST-1,
Transformator 220/120V 0,5A,
Autotransformator,
Dekada rezystancyjna.
Schematy układów pomiarowych.
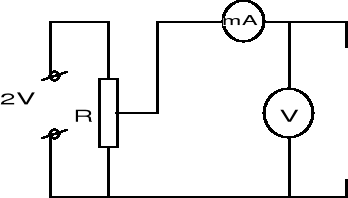
Rys. 1.
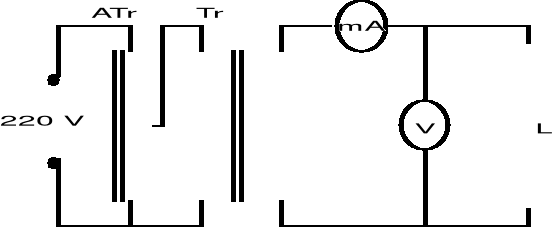
Rys. 2.
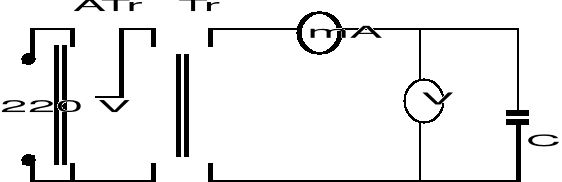
Rys. 3.
Tabele pomiarowe.
Tabela nr.1 (cewka)
Lp. |
U [V] |
I [mA] |
1 |
0,0 |
0,00 |
2 |
0,2 |
4,66 |
3 |
0,4 |
9,23 |
4 |
0,6 |
14,02 |
5 |
0,8 |
18,68 |
6 |
1,0 |
24,16 |
7 |
1,2 |
27,90 |
8 |
1,4 |
32,30 |
9 |
1,6 |
37,10 |
10 |
1,8 |
41,65 |
11 |
2,0 |
46,00 |
Tabela nr. 2 (cewka bez rdzenia) Tabela nr. 3 (cewka z rdzeniem)
Lp. |
U [V] |
I [mA] |
|
Lp. |
U [V] |
I [mA] |
1 |
0,00 |
0,00 |
|
1 |
0,00 |
0,00 |
2 |
0,49 |
8,37 |
|
2 |
0,53 |
2,85 |
3 |
0,97 |
15,05 |
|
3 |
0,98 |
4,93 |
4 |
1,49 |
22,69 |
|
4 |
1,47 |
7,20 |
5 |
1,95 |
29,63 |
|
5 |
1,99 |
9,60 |
6 |
2,46 |
36,94 |
|
6 |
2,51 |
12,00 |
7 |
2,99 |
44,88 |
|
7 |
3,03 |
14,46 |
8 |
3,56 |
53,31 |
|
8 |
3,56 |
16,88 |
9 |
3,97 |
59,63 |
|
9 |
4,04 |
19,10 |
10 |
4,51 |
67,67 |
|
10 |
4,47 |
21,08 |
11 |
5,00 |
74,81 |
|
11 |
5,04 |
23,06 |
12 |
5,53 |
82,40 |
|
12 |
5,45 |
25,54 |
13 |
5,99 |
89,67 |
|
13 |
5,99 |
27,93 |
Tabela nr. 4 (Kondensator C1)
Lp. |
U [V] |
I [mA] |
1 |
0,00 |
0,0000 |
2 |
0,54 |
0,0121 |
3 |
1,04 |
0,0215 |
4 |
1,49 |
0,0305 |
5 |
2,00 |
0,0410 |
6 |
2,49 |
0,0513 |
7 |
3,00 |
0,0610 |
8 |
3,55 |
0,0729 |
9 |
4,07 |
0,0841 |
10 |
4,57 |
0,0940 |
11 |
4,97 |
0,1023 |
12 |
5,49 |
0,1133 |
13 |
6,04 |
0,1250 |
Tabela nr. 5 (Kondensator C2 ) Tabela nr. 6 (Kondensator C3)
Lp. |
U [V] |
I [mA] |
|
Lp. |
U [V] |
I [mA] |
1 |
0,00 |
0,0000 |
|
1 |
0,00 |
0,00 |
2 |
0,53 |
0,0848 |
|
2 |
0,56 |
0,06 |
3 |
0,95 |
0,1374 |
|
3 |
1,01 |
0,21 |
4 |
1,46 |
0,2056 |
|
4 |
1,49 |
0,37 |
5 |
1,99 |
0,2814 |
|
5 |
2,00 |
0,54 |
6 |
2,47 |
0,3447 |
|
6 |
2,49 |
0,70 |
7 |
3,01 |
0,4119 |
|
7 |
3,01 |
0,86 |
8 |
3,46 |
0,4819 |
|
8 |
3,53 |
1,02 |
9 |
3,98 |
0,5563 |
|
9 |
4,01 |
1,18 |
10 |
4,48 |
0,6252 |
|
10 |
4,45 |
1,31 |
11 |
5,04 |
0,7007 |
|
11 |
5,05 |
1,48 |
12 |
5,53 |
0,7704 |
|
12 |
5,50 |
1,64 |
13 |
6,00 |
0,8376 |
|
13 |
6,04 |
1,79 |
Tabela nr. 7 (Szeregowo) Tabela nr. 8 (Równolegle)
Lp. |
U [V] |
I [mA] |
|
Lp. |
U [V] |
I [mA] |
1 |
0,00 |
0,0000 |
|
1 |
0,00 |
0,0000 |
2 |
0,51 |
0,0093 |
|
2 |
0,54 |
0,2835 |
3 |
1,00 |
0,0167 |
|
3 |
1,00 |
0,4818 |
4 |
1,46 |
0,0244 |
|
4 |
1,49 |
0,7066 |
5 |
2,00 |
0,0337 |
|
5 |
2,04 |
0,9711 |
6 |
2,49 |
0,0419 |
|
6 |
2,46 |
1,11 |
7 |
3,00 |
0,0509 |
|
7 |
3,01 |
1,36 |
8 |
3,49 |
0,0590 |
|
8 |
3,53 |
1,60 |
9 |
4,00 |
0,0681 |
|
9 |
4,04 |
1,83 |
10 |
4,50 |
0,0766 |
|
10 |
4,55 |
2,06 |
11 |
4,98 |
0,0846 |
|
11 |
4,99 |
2,27 |
12 |
5,48 |
0,0935 |
|
12 |
5,50 |
2,50 |
13 |
6,00 |
0,1021 |
|
13 |
6,00 |
2,73 |
Opracowanie wyników pomiarowych.
Cewka zasilana prądem stałym.
Na podstawie charakterystyki prądowo napięciowej cewki widać, że jej rezystancja zależy w sposób liniowy od przyłożonego napięcia. Można więc obliczyć ją ze wzoru R=U/I . Metodą regresji liniowej wyznaczamy współczynniki a, b prostej najbardziej zbliżonej do przebiegu otrzymanego w wyniku pomiarów. Otrzymujemy następujące wartości:
a = 23,06[10-3/Ω] b = 0,18[mA]
I = aU + b
Rezystancja cewki wynosi:
R = 43,03 ± 0,39 [Ω]
Cewka zasilana prądem zmiennym.
Podobnie jak w przypadku zasilania cewki prądem stałym, jej charakterystyka ma charakter liniowy. Impedancję cewki można więc obliczyć ze wzoru Z=U/I . Metodą regresji liniowej wyznaczamy współczynniki a, b prostej najbardziej zbliżonej do przebiegu otrzymanego w wyniku pomiarów. Otrzymujemy następujące wartości:
Dla cewki bez rdzenia:
a = 14,85[10-3/Ω] b = 0,55[mA]
Dla cewki z rdzeniem:
a = 4,61[10-3/Ω] b = 0,35[mA]
I = aU + b
Impedancja cewki wynosi:
Dla cewki bez rdzenia:
Z = 66,84 ± 0,24 [Ω]
Dla cewki z rdzeniem:
Z = 213,68 ± 1,92 [Ω]
Ze wzoru ![]()
obliczamy współczynnik samoindukcji:
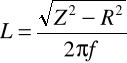
gdzie f = 50 Hz.
Otrzymujemy:
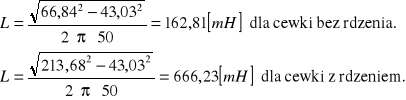
Kondensatory.Na podstawie charakterystyki prądowo napięciowej kondensatorów C1 , C2 , C3 widać, że ich reaktancja zależy w sposób liniowy od przyłożonego napięcia. Można więc obliczyć ją ze wzoru X=U/I . Metodą regresji liniowej wyznaczamy współczynniki a, b prostej najbardziej zbliżonej do przebiegu otrzymanego w wyniku pomiarów. Otrzymujemy następujące wartości:
Dla C1:
a = 0,021[10-3/Ω] b = 0
Dla C2:
a = 0,138[10-3/Ω] b = 0,004[mA]
Dla C3 :
a = 0,309[10-3/Ω] b = -0,072[mA]
Dla szeregowego połączenia kondensatorów C1 , C2 , C3 :
a = 0,017[10-3/Ω] b = 0
Dla równoległego połączenia kondensatorów C1 , C2 , C3 :
a = 0,449[10-3/Ω] b = 0,024[mA]
I = aU + b
Reaktancje poszczególnych kondensatorów wynoszą odpowiednio:Dla kondensatora C1 :
X=47619,05 ± 198,72 []
Dla kondensatora C2 :
X=7204,61± 40,83 []
Dla kondensatora C3 :
X=3394,43 ± 63,31 []
Dla kondensatorów C1 , C2 , C3 połączonych szeregowo:
X=58823,53 ± 221,31 []
Dla kondensatorów C1 , C2 , C3 połączonych równolegle:
X=2203,61 ± 82,11 []
Na podstawie tych danych obliczyliśmy pojemności według wzoru:
![]()
otrzymujemy:
C1 = 66,85 nF
C2 = 441,81 nF
C3 = 937,74 nF
C1 , C2 , C3 szeregowo = 54,11 nF
C1 , C2 , C3 równolegle = 1,44 μF
Analiza błędów.
Błędy liczymy metodą różniczki zupełnej. Błędy obliczenia impedancji cewek i reaktancji kondensatorów wykonaliśmy używając programu komputerowego.
Błąd obliczenia współczynnika samoindukcyjności:
dla cewki bez rdzenia:
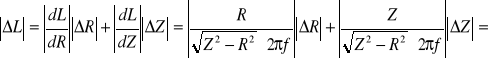
1,31[mH]
dla cewki z rdzeniem:
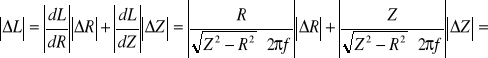
6,24[mH]
Błąd obliczenia pojemności kondensatorów obliczamy ze wzoru:
![]()
Dla kondensatora C1 :
ΔC1= 0,28 [nF]
Dla kondensatora C2 :
ΔC2= 2,50 [nF]
Dla kondensatora C3 :
ΔC3= 17,49 [nF]
Dla kondensatorów C1 , C2 , C3 połączonych szeregowo:
ΔCs= 0,20 [nF]
Dla kondensatorów C1 , C2 , C3 połączonych równolegle:
ΔCr= 0,05 [μF]
Wnioski i uwagi.
Po wykonaniu obliczeń indukcyjności, pojemności, rezystancji i impedancji oraz po uwzględnieniu błędu otrzymaliśmy następujące wartości:
Rezystancja cewki zasilanej prądem stałym wynosi:
R = 43,03 ± 0,39 [Ω]
Impedancja oraz współczynnik indukcji własnej cewki zasilanej prądem zmiennym (f=50[Hz])
Bez rdzenia:
Z = 66,84 ± 0,24 [Ω], L = 162,81 ± 1,31 [mH]
Z rdzeniem:
Z = 213,68 ± 1,92 [Ω], L = 666,23 ± 6,24 [mH]
Pojemności oraz reaktancje poszczególnych kondensatorów wynoszą:
Kondensatora C1 :
C1= 66,85 ± 0,28 [nF], X = 47619,05 ± 198,72 [Ω]
Kondensatora C2 :
C2= 441,81 ± 2,50 [nF], X = 7204,61 ± 40,83 [Ω]
Kondensatora C3 :
C3= 937,74 ± 17,49 [nF], X = 3394,43 ± 63,31 [Ω]
Dla kondensatorów C1 , C2 , C3 połączonych szeregowo:
Cs= 54,11 ± 0,20 [nF], X = 58823,53 ± 221,31 [Ω]
Dla kondensatorów C1 , C2 , C3 połączonych równolegle:
Cr= 1,44 ± 0,05 [μF], X = 2203,61 ± 82,11 [Ω]
W celu dodatkowego sprawdzenia poprawności wyznaczenia pojemności kondensatorów sprawdziliśmy czy zachodzą zależności 1/Cs=1/C1+1/C2+1/C3 oraz Cr=C1+C2+C3, wynikające z szeregowego i równoległego połączenia tych elementów. Otrzymaliśmy następujące wyniki:
dla połączenia szeregowego:
1/Cs=1/C1+1/C2+1/C3
1/54,11.10-9=1/54,68.10-9
54,11 [nF] = 54,68 [nF]
dla połączenia równoległego:
Cr=C1+C2+C3
1,44 [μF] = 1,45 [μF]
Zgodność wyników świadczy o prawidłowym wyznaczeniu badanych pojemności.
Charakterystyka cewki zasilanej prądem stałym ma charakter lini�owy, co zgadza się z przewidywaniami teoretycznymi według których element ten w takich warunkach pracy zachowuje się jak rezystor. Charakterystyki cewki zasilanej prądem zmiennym również mają charakter liniowy. Wynika to z tego, że była ona badana przy stałej częstotliwości. Po porównaniu cewki z rdzeniem i bez widać, że cewka z rdzenie ma większą impedancję. Na charakterystykach prądowo napięciowych kondesatorów widać, że ich reaktancjaa ściśle zależy od pojemności. Ze wzrotem pojemności maleje reaktancjaa.
Pomiary indukcyjności i pojemności metodą techniczną
- -
Wyszukiwarka
Podobne podstrony:
7 W INDUK MOJE , Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Lepkość-sciaga, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Nr ćwiczenia5 moje, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[4]tabelka, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[8]konspekt new, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
FIZYK~47, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizyka
3 W LEPKO CIECZY, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labor
[3]opracowanie v1.0, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
kospekt12, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 12 Wyznaczanie
PUZON, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki s
cw8 wyniki, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, labo
[4]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
mostek Wheatstone'a(1), Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, l
za, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, laborki fizy
konspekt nr8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fi
[7]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
konspekt 8, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Fizy
więcej podobnych podstron