3. OBLICZANIE WAŁKÓW

I ŁOŻYSK TOCZNYCH

3.1. Rozmieszczenie kół w skrzynce prędkości

Do obliczeń wałków i łożysk tocznych są potrzebne wartości sił działających na koła zębate osadzone na tych wałkach, ich rozmieszczenie względem podpór, rozstaw łożysk oraz prędkość obrotowa wałka. Wartości sił można obliczyć z założonej mocy przenoszonej przez czynne przekładnie elementarne, z ich prędkości obrotowej i ze średnic kół.

Do określenia miejsc przyłożenia sił na wałkach są potrzebne dane o rozmieszczeniu kół w reduktorze. Przedstawiony niżej program komputerowy pozwala na rozmieszczanie kół zębatych, narysowanych symbolicznie w postaci prostokątów, na rozwiniętym przekroju reduktora.

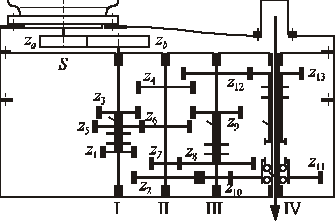
Rys. 3.1. Schemat kinematyczny napędu głównego wiertarki

(wykres przełożeń na rys. 1.13)

Na rysunku 3.1 pokazano schemat kinematyczny napędu głównego wiertarki zgodny z danymi używanymi w przykładzie obliczeń kinematycznych na rysunkach 1.12 i 1.13. Na początku napędu przewidziano przekładnię z_a/z_b, składającą się z koła stalowego i tekstolitowego, dopasowującą poziom prędkości obrotowej wrzeciona do wymagań użytkownika.

Na podstawie obliczeń wytrzymałościowych kół zębatych z tego przykładu (rys. 2.12, 2.13 i 2.14) wprowadzono do programu dane o wielkościach kół. Te dane oraz współrzędne kół są przechowywane w zbiorze danych pod hasłem wpisanym do tablicy (PRZYKŁAD na rys. 3.2) i wywoływane na to hasło. Nie trzeba zatem powtórnie wprowadzać danych, gdy zaistnieje konieczność dokonania jedynie drobnych poprawek.

Rys. 3.2. Obraz ekranu podczas wprowadzania danych do programu rozmieszczania kół w skrzynce prędkości (wartości liczbowe z przykładu na rys. 1.12 i 1.13)

Po wprowadzeniu danych ukazuje się graficzny obraz ekranu z proporcjonalnie narysowanymi kołami * 1 mm szerokości koła odpowiada 1 pikselowi (zatem grubość linii wynosi także 1 mm). Koło wyróżnione kolorem (po zatwierdzeniu wyboru przyciskiem ENTER) można przemieszczać w prawo lub w lewo przyciskami kierunkowymi klawiatury z małą prędkością lub 8-krotnie większą (CTRL + przycisk kierunkowy). Po naciśnięciu ENTER koło pozostaje w wybranym położeniu, a wtedy przyciskami kierunkowymi (prawo, lewo, góra, dół) można wybrać następny element do układania. Czerwone linie graniczne są odległe o 19 mm od orientacyjnego położenia środków łożysk. Jeżeli rozmieszczenie kół jest zadowalające, to naciśnięcie przycisku ESC kończy procedurę układania skrzynki. Na ekranie są wypisane dane o rozłożeniu sił (położenie środków kół stałych), wartości średnic kół oraz efektywne prędkości obrotowe wałków reduktora.

Rys. 3.3. Wydruk wyników programu rozmieszczania kół w skrzynce prędkości

Graficzny wydruk ekranu, przedstawiony dla omawianego przykładu na rysunku 3.3, jest dla konstruktora przydatnym zestawem informacji do obliczeń wałków i łożysk tocznych projektowanego napędu.

3.2. Założenia obliczeń wałków i łożysk

Wałki w skrzynkach prędkości obrabiarek powinny spełniać warunek wytrzymałościowy na zginanie (zmęczeniowe) oraz powinny mieć odpowiednią sztywność. Wymaganie dużej sztywności jest zazwyczaj znacznie ostrzejsze od warunku wytrzymałościowego, ponieważ:

* ugięcia wałków (kąty ugięcia) wpływają na rozkład naprężeń w zazębieniach i prowadzą do niekorzystnego, trapezowego lub nawet trójkątnego rozkładu nacisków powierzchniowych wzdłuż linii zębów,

* zbyt duże kąty ugięcia wałka na podporach (w łożyskach) wpływają ujemnie na trwałość łożysk,

* małe sztywności wałków są przyczyną hałaśliwej pracy przekładni.

Praktycznie przydatne kryterium sztywności [6] określa dopuszczalną strzałkę ugięcia wałka jako (0,0001*0,0005) część rozstawu podpór. Do obliczeń wałków w reduktorach średniej wielkości przyjęto zatem wartość średnią:

. (3.1)

Na rysunku 3.4 pokazano schemat obciążenia siłą skupioną belki statycznie wyznaczalnej opartej na dwóch podporach. Linia ugięcia takiej belki o jednakowym przekroju jest krzywą trzeciego stopnia, a jej największa strzałka ugięcia niewiele różni się od ugięcia belki w połowie długości. Gdy siła znajduje się blisko podpory (a → 0), to f_max / f(l / 2) = 1,0264, ugięcia belki pochodzące od kilku sił można sumować w połowie długości belki z praktycznie wystarczającą dokładnością.

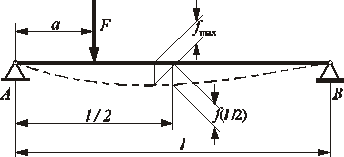
Rys. 3.4. Linia ugięcia belki obciążonej jedną siłą skupioną

Najczęściej na wałek działają dwie siły pochodzące od wejścia i wyjścia napędu. Przed zwinięciem skrzynki prędkości, gdy nie jest znany kierunek tych sił w przestrzeni, można przyjąć założenie upraszczające, że siły obliczeniowe są styczne do okręgów podziałowych, że są do siebie równoległe, a wywołane przez nie ugięcia sumują się arytmetycznie. Wałek obliczony z takim założeniem będzie miał korzystniejsze warunki pracy w prawie każdym zwinięciu skrzynki prędkości. Wyjątek stanowią równoległe siły wypadkowe, styczne do okręgów zasadniczych, które są większe od obwodowych jedynie o 6%, lecz ich oddziaływanie na wałek daje większe ugięcia tylko przy jednym kierunku obrotów, ponieważ po zmianie kierunku ruchu ugięcia są znacznie mniejsze niż w modelu uproszczonym.

Strzałkę ugięcia wałka w połowie jego długości, pochodzącą od siły działającej między podporami w odległości a od bliższej podpory, wyraża się wzorem:

, (3.2)

a strzałkę ugiecia pochodzącą od siły działającej poza podporą, w odległości a od niej, wyraża zależność:

. (3.3)

Po dodaniu ugięć spowodowanych obiema siłami, wyznaczonymi z mocy, prędkości obrotowej wałka oraz średnic podziałowych kół, i przyrównaniu wyniku do wartości dopuszczalnej (0,0003l) można obliczyć najmniejszy wymagany moment bezwładności przekroju wałka. Model geometryczny wałka do takich obliczeń przedstawia rysunek 3.5.

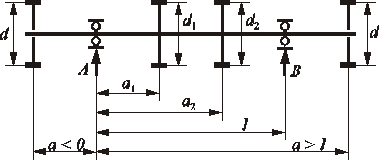
Rys. 3.5. Model geometryczny do obliczeń wałków i łożysk tocznych

Minimalną średnicę wałka oblicza się według wzoru ogólnego:

, (3.4)

gdzie

. (3.5)

Dla wałków stalowych, dla których E = 2,06 ⋅ 10⁵ MPa, otrzymuje się F = 16. Składniki Y₁ i Y₂ oblicza się zależnie od miejsca przyłożenia sił. Ponieważ we wzorze (3.2) odległość a jest mierzona od siły do bliższej podpory, zatem wartość Y (Y₁ lub Y₂) jest obliczana ze wzoru niezależnego od tego warunku. Odległość a we wzorze (3.6) jest mierzona zawsze od podpory A.

Dla 0 < a < l

, (3.6)

dla a < 0

, (3.7)

dla a > l

. (3.8)

Model geometryczny (rys. 3.5), jednoznacznie określający miejsce środków kół osadzonych na wałku, a tym samym położenie sił działających na wałek, umożliwia wyznaczenie reakcji podpór A i B. Znając prędkość obrotową wałka oraz przewidując trwałość łożysk (kulkowych), można wyznaczyć wymaganą nośność ruchową według wzorów:

[N] , (3.9)

[N] , (3.10)

gdzie

. (3.11)

Trwałość łożyska T_h [h] oznacza redukowany czas jego pracy w warunkach największego obciążenia, przyjętych do obliczeń. Na podstawie przykładów z literatury [6] oraz obserwacji reduktorów pracujących w eksploatowanych obrabiarkach można przyjąć zastępczą trwałość łożysk kulkowych * 5000 godzin pracy pod największym obciążeniem, co odpowiada około 20 000 godzin eksploatacji obrabiarki. Z takiego założenia otrzymuje się C = 12 785 230.

Wartości bezwzględne składników występujących we wzorach (3.9) i (3.10) prowadzą do wyznaczania reakcji podpór, będących arytmetycznymi sumami części tych reakcji na działanie obu sił na wałek. Podobnie jak w obliczeniach ugięcia wałka istnieje nieograniczona możliwość układania osi wałków reduktora w zwinięciu. W przypadkach wątpliwych, np. po przyjęciu łożyska o nośności ruchowej mniejszej od obliczonej, należy wykonać obliczenia sprawdzające po opracowaniu zwinięcia skrzynki prędkości.

3.3. Algorytm obliczeń wałków i łożysk kulkowych

Wstępne obliczenia wałków i łożysk, omówione w rozdziałach 3.1*3.3, można wykonać przed konstruowaniem napędu głównego. Zestawienie wyników obliczeń całego reduktora ułatwia unifikację rozwiązań wałków i łożysk. Zgodnie z założeniami obliczenia sprawdzające po opracowaniu konstrukcji nie są konieczne.

Rozmieszczenie kół zębatych w reduktorze

Wstępne opracowanie rozwinięcia napędu, omówione w rozdziale 3.1, pozwala na określenie miejsc działania sił przenoszących napęd. Przyjęto założenie, że wektory sił działających na dany wałek są równoległe, a ich skutki sumują się arytmetycznie (ugięcia wałków, reakcje podpór).

Wprowadzanie danych

Na rysunku 3.6 pokazano obraz ekranu podczas wprowadzania danych. Wartości mocy i prędkości obrotowej służą do obliczenia momentu obrotowego działającego na wałek w danym wariancie obciążenia, a siłę oblicza się, dzieląc ten moment przez połowę średnicy koła. W przekładni pasowej oprócz siły obwodowej istnieje siła naciągu wstępnego pasów, którą oszacowano na 25% największej siły czynnej, zatem zalecono wpisanie średnicy koła pasów klinowych jako 80% średnicy skutecznej.

Jeżeli na wejściu napędu do reduktora przewidziano sprzęgło przenoszące tylko moment obrotowy (lub w taki sposób napęd wychodzi z reduktora), to nie podaje się średnicy koła (d₁ lub d₂ = 0), a moment ten jest obliczany z mocy i prędkości obrotowej. Podawanie prędkości obrotowej na wejściu napędu jest zatem konieczne.

Z kilku prędkości obrotowych wałka, które są możliwe w danym wariancie zazębienia, należy podać najmniejsze, ponieważ przy stałej mocy napędu im towarzyszą największe momenty i siły.

Wprowadzanie danych jest zakończone, jeśli dla kolejnego numeru wałka nie będzie wpisana moc obliczeniowa.

Rys. 3.6. Obraz na ekranie monitora podczas wprowadzania danych do obliczeń

wałków i łożysk kulkowych (dane z przykładu na rys. 3.3 dla wałka III)

Korekta danych

Wprowadzone wartości mocy i prędkości obrotowych według powyższych zasad odpowiadają zakresowi stałej mocy, który nie obejmuje wszystkich kombinacji danych wejścia i wyjścia napędu. Przegląd tych kombinacji ma na celu nie tylko usuwanie błędów, lecz także wprowadzenie zmian prędkości i mocy obliczeniowej w zakresie stałego momentu.

W przykładzie pokazanym na rysunku 3.7 ostatnia kombinacja danych (wariant III₄) znajduje się w zakresie stałego momentu, zatem początkowo wprowadzona prędkość obrotowa 169 obr/min musiała być zmieniona na 423 obr/min, zgodnie z wykresem przełożeń przedstawionym na rysunku 1.13 oraz przyjętą granicą zakresu stałej mocy i stałego momentu n' = 125 obr/min. Otrzymano w ten sposób zgodność danych: mocy obliczeniowej i prędkości obrotowej wpisanych w rubrykach tablicy.

Rys. 3.7. Obraz na ekranie monitora podczas korekty danych do obliczeń wałków

i łożysk kulkowych w wariantach ograniczonych zakresem stałej mocy napędu

W niektórych wariantach obciążenia wałka w zakresie stałego momentu jest przenoszona tylko moc mniejsza od wpisanej na etapie wprowadzania danych, wtedy należy wpisać tę mniejszą wartość.

W zakresie stałego momentu:

* moment przenoszony przez końcowe przekładnie jest największy,

* siły międzyzębne są (w tych przekładniach) największe i stałe,

* moc przenoszona przez przekładnię jest proporcjonalna do prędkości obrotowej.

Ponieważ wymagana nośność ruchowa łożysk tocznych jest zależna nie tylko od sił, lecz także od prędkości obrotowych, zatem z zakresu stałych sił (stałego momentu) należy wybrać największą prędkość obrotową przenoszoną w obliczanej kombinacji zazębienia.

Interpretacja wyników

Wyniki obliczeń wszystkich wałków i łożysk reduktora wydrukowane w jednym zestawieniu (rys. 3.8) ułatwiają unifikację rozwiązań projektowanej skrzynki prędkości. Z przedstawionego zestawienia wynika, że wszystkie wałki reduktora mogą być zaprojektowane jako wielowypustowe o jednakowych średnicach
∅28 mm/∅32 mm (średnica zastępcza wynosi ∅30,006 mm) i o średnicy ∅25 mm w czopach łożyskowych. Można także dobrać łożyska 6205 o nośności ruchowej 11 000 N lub 6305 o nośności 17 300 N.

Zestawienie łożysk z podziałem na podpory A i B (strony korpusu) ułatwia technologiczne rozmieszczenie otworów w ścianach korpusu pod łożyska różnej wielkości.

Rys. 3.8. Wyniki obliczeń wałków i łożysk kulkowych (dane z przykładu na rys. 3.3)

Tablica wyników zawiera miejsca nie wypełnione, przeznaczone na wpisanie średnic wałków i numerów łożysk wybranych przez konstruktora.

3.4. Sprawdzające obliczenia wrzecion

Sprawdzające obliczenia wrzeciona wykonuje się po wstępnym opracowaniu konstrukcji, gdy są znane jego wymiary. Wyniki obliczeń są interpretowane przez konstruktora i mogą być wskazówką co do potrzeby wprowadzenia zmian konstrukcyjnych. Jako kryteria oceny przyjęto:

* największą strzałkę ugięcia między podporami wrzeciona obciążonego siłami poprzecznymi (tokarki, frezarki itp.),

* naprężenia skręcające wrzeciona obciążonego momentem obrotowym (np. wiertarki).

Jako wartości dopuszczalne [6] przyjęto:

* strzałkę ugięcia wrzeciona f_dop = 0,0001* l (l * rozstaw poprzecznych łożysk wrzeciona),

* naprężenia dopuszczalne na skręcanie k_s = 40 MPa.

Są to dość ostre ograniczenia, dlatego po obliczeniach komputerowych jest podawany 3-stopniowy komentarz, że wyniki obliczeń są:

* dopuszczalne (gdy wartość obliczona jest co najwyżej równa dopuszczalnej),

* zbyt duże (gdy wynik nie przekracza dwukrotnej wartości dopuszczalnej),

* niebezpieczne (gdy wynik jest większy od dwukrotnej wartości dopuszczalnej).

Rys. 3.9. Obraz na ekranie monitora podczas określania rodzaju obciążenia wrzeciona

Na rysunku 3.9 pokazano obraz ekranu podczas wyboru sposobu sprawdzania wrzeciona: wybiera się rodzaj obciążenia przez wyróżnienie napisu kolorem i zatwierdza ten wybór przyciskiem ENTER.

Wrzeciono może być obciążone siłami poprzecznymi na kole zębatym (pasowym) na wejściu napędu oraz siłą skrawania na wyjściu. Do tablicy danych (rys. 3.10) wprowadza się parametry, z których można te siły wyznaczyć * siłę skrawania jako iloraz mocy i prędkości skrawania:

[N] (3.12)

oraz siłę na kole zębatym (lub pasowym):

[N] . (3.13)

Przy założeniu, że efekty obu tych sił sumują się arytmetycznie, oraz z warunku równowagi momentów względem środka łożyska poprzecznego w głównym węźle łożyskowym (prawa podpora na rys. 3.10) można wyznaczyć reakcję w drugiej podporze za pomocą wzoru:

. (3.14)

Rys. 3.10. Obraz ekranu monitora po wprowadzeniu danych do obliczeń ugięcia wrzeciona

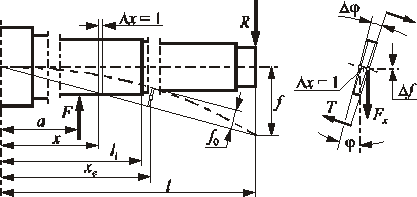
Rys. 3.11. Model geometryczny obliczania ugięcia wrzeciona jako wałka

wielostopniowego

W modelu matematycznym przedstawionym na rysunku 3.11 założono, że wałek wielostopniowy, jakim jest wrzeciono, jest utwierdzony w głównym węźle łożyskowym i obciążony siłą na kole osadzonym między podporami oraz reakcją w drugiej podporze. Oblicza się ugięcie końca takiej belki, a następnie ugięcie maksymalne f₀ względem linii łączącej końce belki, czyli względem podpór. Z podanych wartości D_i i d₀ oblicza się momenty bezwładności przekrojów, a długości poszczególnych stopni średnic przelicza się na odległości l_i (rys. 3.11) od głównego węzła łożyskowego.

Założono, że wymiary są podawane w milimetrach. Ponieważ jednostka ta jest mała w porównaniu z długością wrzeciona, 1 mm może służyć jako przyrost elementarny w całkowaniu numerycznym. Przez zastosowanie Δx = 1 wzory opisujące przyrosty kąta i strzałki ugięcia przyjmują szczególnie prostą postać:

, (3.15)

. (3.16)

DANE: l, a, F, R l0, l1, l2 … li … J0, J1, J2 … Ji …

PODPROGRAM f

x = 0; φ = 0; f= 0; i = 0

x = x + 1

q = 1

x > li

TAK

i = i + 1

PODPROGRAM f

TAK

x > a

NIE

PODPROGRAM f

WYNIK:

x < l i Δf < q

TAK

NIE

Rys. 3.12. Algorytm obliczeń numerycznych ugięcia wrzeciona

Obliczenia, których algorytm przedstawiono na rysunku 3.12, są prowadzone w dwóch przebiegach przez ten sam podprogram zawierający pętlę warunkową (x < 1 i ϕ < q). W pierwszym przebiegu założono, że q = 1, zatem warunek ϕ < q jest spełniony zawsze, bowiem kąt ugięcia ϕ jest mały. Po zakończeniu obiegów pętli, gdy x = 1, otrzymuje się ugięcie f belki wielostopniowej utwierdzonej jednostronnie, zatem wartość q = f/l jest średnim kątem ugięcia tej belki. W drugim przebiegu obliczenia są kontynuowane, gdy Δf < q, czyli do punktu ekstremum. W tym miejscu (x_e na rys. 3.11) jest obliczane ugięcie wrzeciona jako wałka na dwóch podporach.

Wynik obliczeń jest przedstawiony na ekranie w trybie graficznym (rys. 3.13) i w tej postaci może być wydrukowany. Oprócz podstawowych danych liczbowych zawiera on zarys wrzeciona na odcinku między podporami, narysowany proporcjonalnie do wymiarów wprowadzonych jako dane. Proporcjonalnie jest także odwzorowane miejsce przyłożenia sił oraz położenie punktu o największej strzałce ugięcia.

Rys. 3.13. Wyniki obliczeń ugięcia wrzeciona

W przedstawionym przykładzie liczbowym ugięcie wrzeciona zostało ocenione przez program jako zbyt duże, choć przekroczono wartość dopuszczalną zaledwie o 0,5%. Ostateczna interpretacja wyników należy do konstruktora.

Wrzeciona wiertarek i podobnych maszyn są obciążone tylko momentem skręcającym, przekazywanym na nie najczęściej przez przesuwne połączenie wielowypustowe. Część wielowypustowa wrzeciona ma zazwyczaj najmniejszy wskaźnik przekroju na skręcanie, zatem w tym przekroju należy sprawdzić naprężenia.

Rys. 3.14. Obraz ekranu monitora po wprowadzeniu danych do obliczeń wrzeciona na skręcanie (wybrano wielowypust ogólnego przeznaczenia 6∗28∗32)

Na rysunku 3.14 przedstawiono obraz ekranu po wprowadzeniu danych do obliczeń. Rodzaj połączenia wielowypustowego jest wybierany z lewej tablicy. Do innego przekroju (np. kołowego) można wybrać odpowiedni wielowypust, wiedząc, że zastępcza średnica jest w przybliżeniu równa średniej arytmetycznej zewnętrznej i wewnętrznej średnicy wielowypustu. Program liczący zawiera gotową tablicę wskaźników przekrojów wielowypustowych do obliczeń na skręcanie.

Rys. 3.15. Wyniki obliczeń wrzeciona na skręcanie

Moment obrotowy jest obliczany jako iloraz mocy i prędkości obrotowej, a naprężenia skręcające jako iloraz momentu i wskaźnika przekroju, zatem:

[MPa] . (3.17)

Wielkości w tym wzorze są wyrażone w następujących jednostkach: P₀ w kilowatach, n' w obrotach na minutę, a W₀ w milimetrach sześciennych.

Wynik obliczeń przedstawiony na rysunku 3.15 jest wydrukowanym obrazem graficznym ekranu monitora. W przedstawionym przykładzie naprężenia są o 17,5% większe od wstępnie założonej wartości dopuszczalnej, stąd komentarz zbyt duże na rysunku 3.14. Interpretacja tego wyniku należy do konstruktora.

62

3. Obliczanie wałków i łożysk tocznych

49

3.1. Rozmieszczenie kół w skrzynce prędkości

51

3.2. Założenia obliczeń wałków i łożysk

55

3.3. Algorytm obliczeń wałków i łożysk kulkowych

61

3.4. Sprawdzające obliczenia wrzecion

---