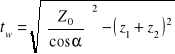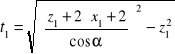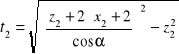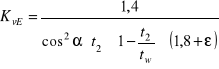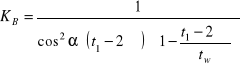2. OBLICZANIE KÓŁ ZĘBATYCH

2.1. Własności materiałów stosowanych na koła zębate

Najczęstszymi przypadkami uszkodzeń kół zębatych w skrzynkach prędkości obrabiarek [6] są:

* złamania doraźne zębów na skutek wad materiałowych, wadliwej obróbki cieplnej lub przeciążenia,

* zużycie zmęczeniowe warstwy wierzchniej boków zębów (pitting) na skutek zmiennych nacisków.

Inne rodzaje uszkodzeń, np. złom zmęczeniowy czy wgniecenia na skutek doraźnych przeciążeń, występują rzadziej.

Istotnymi cechami materiału stosowanego na koła zębate są zatem: wytrzymałość zmęczeniowa na naciski powierzchniowe (przede wszystkim) oraz na zginanie.

Przyjęto dwa sposoby określania naprężeń powierzchniowych (rys. 2.1): według modelu Hertza (p_max) lub Stribecka (k_p). W obu modelach styk dwóch powierzchni walcowych można sprowadzić do przypadku walca o sumarycznej krzywiźnie (zastępczym promieniu krzywizny) i płaszczyzny.

Według założeń Hertza stykają się ze sobą materiały jednorodne, a odkształcenia w obszarze styku występują w granicach sprężystości, zatem wywołują proporcjonalne do nich naprężenia o rozkładzie eliptycznym (rys. 2.1). Największą wartość naprężenia na powierzchni styku wyraża się wzorem:

, (2.1)

gdzie: ν₁, ,ν₂ * liczby Poissona, E₁, E₂ * moduły sprężystości stykających się materiałów, ρ * zastępczy promień krzywizny.

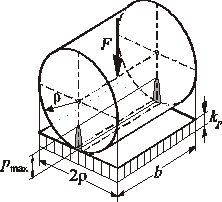
Rys. 2.1. Porównanie modelu naprężeń stykowych Hertza (p) i wskaźnika naprężeń Stribecka (k_p)

Wskaźnik naprężeń powierzchniowych według modelu Stribecka jest równy
ilorazowi siły nacisku i pola rzutu walca (o krzywiźnie zastępczej) na płaszczyznę:

. (2.2)

Między wskaźnikiem naprężeń Stribecka a naprężeniami Hertza istnieje jednoznaczny związek:

(2.3)

lub dla jednorodnych materiałów, gdy ν₁ = ν₂ = ν i E₁ = E₂ = E:

. (2.4)

Prostsza postać wzoru Stribecka w porównaniu ze wzorem Hertza, umożliwiająca ocenę naprężeń w miejscu styku za pomocą wskaźnika obliczonego jedynie z wartości siły i krzywizny stykających się powierzchni, sprzyja jego rozpowszechnieniu. Przyjęto go także w tej pracy.

Autorzy badający wytrzymałość kół zębatych [1, 3] są zgodni co do tego, że wytrzymałość zmęczeniowa materiałów na naciski powierzchniowe jest zależna od twardości warstwy wierzchniej. Zależność tę [1] określono jako proporcjonalną do kwadratu twardości wyrażonej w skali Brinella:

. (2.5)

W tym wzorze zarówno twardość (HB), jak i wytrzymałość (Z_p) są wyrażone w takich samych jednostkach (kilogramach-siły na milimetr kwadratowy).

Zróżnicowanie wytrzymałości na naciski powierzchniowe spowodowane obróbką cieplną stali [6] wynika przede wszystkim z różnych twardości warstwy wierzchniej (rys. 2.2, linie 1a, 1b, 1c).

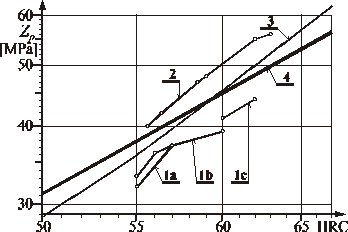
Rys. 2.2. Wytrzymałość zmęczeniowa stali na naciski powierzchniowe (wskaźnik

Stribecka) w funkcji twardości Rockwella według różnych źródeł; 1 * Wrotny [6]:

1a * hartowana w kąpieli cyjanowej, 1b * hartowana powierzchniowo, 1c * nawęglana i hartowana, 2 * M*ler [3], 3 * Kocańda [1] * wzór liczbowy, 4 * wzór (2.6);

wartości liczbowe sprowadzono do wspólnych jednostek

Badania wytrzymałościowe materiałów kół zębatych na naciski powierzchniowe wykonuje się dla 10⁸ cykli zmian obciążenia [3]. Dla stali bardzo twardych (powyżej 57 HRC) załamanie krzywej wytrzymałości * wytrzymałość trwała * może nie wystąpić. Wówczas przyjmuje się wartość wytrzymałości zmęczeniowej dla 10⁸ cykli. Jeśli zatem istnieje trwała wytrzymałość twardych stali, to pojawi się ona poza przyjętym zakresem i będzie mniejsza od zbadanej. Koła zębate w przekładniach obrabiarkowych podczas eksploatacji mogą być poddane większej liczbie zmian obciążenia. Stąd propozycja autora, aby wytrzymałość powierzchniową wyznaczać w funkcji twardości Rockwella, ponieważ skala ta w zakresie dużych twardości rośnie wolniej niż skala Brinella. Zależność tę, słuszną w zakresie twardości powyżej 40 HRC, można określić wzorem:

. (2.6)

Graficznym obrazem tej zależności jest linia 4 na rysunku 2.2, przebiegająca pomiędzy wartościami zaczerpniętymi z literatury.

Naprężenia dopuszczalne wyraża się jako iloraz wytrzymałości i współczynnika bezpieczeństwa:

, (2.7)

gdzie

. (2.8)

Współczynnik bezpieczeństwa wyrażony wzorem (2.8) jest funkcją czynników o znaczeniu i wartościach podanych niżej:

x_H * współczynnik zależny od wielkości koła i związanej z tym odchyłki twardości; jeśli przyjmie się odchyłkę 3 HRC przy średniej twardości 50 HRC, otrzymuje się x_H = 1,06²; zależność kwadratowa wynika ze wzoru (2.6);

x_Ra * współczynnik zależny od chropowatości powierzchni zębów; dla Ra =
= 1,25 μm x_Ra = 1,04 [3];

x_m * współczynnik zależny od szacowanej dokładności metody obliczeń i od czynników nie uwzględnionych osobno; przyjęto x_m = 1,2;

y_h * współczynnik zależny od lepkości oleju smarującego (przyjęto 100 cSt) i prędkości obwodowej kół zębatych (dla obliczanych przypadków przyjęto 1 m/s * małe prędkości przy dużych siłach); y_h = 0,709 [3].

Dla wyszczególnionych warunków pracy współczynnik bezpieczeństwa x_p = 2. Wartość tę wstawiono do wzorów (2.6) i (2.7) i wyznaczono zależność między dopuszczalnymi wskaźnikami naprężeń na powierzchni zębów kół przekładni obrabiarkowych a twardością materiału tych kół:

. (2.9)

W odróżnieniu od wytrzymałości stykowej wytrzymałość na zginanie nie może być wyrażona w funkcji innej wybranej cechy materiału, np. twardości. Naprężenia dopuszczalne są specyficzną cechą materiału, warunków pracy przekładni, a także wielkości zębów (modułu). Z tego powodu naprężenia dopuszczalne na zginanie przyjęto z literatury specjalistycznej [6], ponieważ są one dostosowane do przekładni obrabiarkowych i wyznaczone na podstawie wytrzymałości trwałej. Dodatkowo przeliczono je dla dużego zakresu modułów (do 10 mm).

W tablicy doboru materiału programu komputerowego do obliczeń wytrzymałościowych przekładni zębatych, przedstawionej na rysunku 2.3, ograniczono się do materiałów najczęściej stosowanych. Podano jedynie naprężenia dopuszczalne na zginanie jednostronne (k_gj), ponieważ dla zginania obustronnego przyjmuje się:

. (2.10)

Rys. 2.3. Obraz na ekranie monitora podczas wyboru materiału na koła zębate

2.2. Obciążenie obliczeniowe przekładni elementarnej

Podstawowym obciążeniem przekładni elementarnej jest moment obrotowy działający na jedno z jej kół zębatych. Znając ten moment oraz średnicę koła, można obliczyć siłę działającą na zęby. Obliczeniową moc oraz obliczeniowy moment obrotowy przekładni elementarnej można wyrazić wzorami:

, (2.11)

, (2.12)

gdzie: P_S  moc silnika [kW], n₀  obliczeniowa prędkość obrotowa [obr/min].

Współczynnik obliczeniowy C₀ jest iloczynem dopuszczalnego współczynnika przeciążenia i sprawności podzespołów napędu od silnika do obliczanej przekładni. Współczynnik ten uwzględnia także charakterystyczne cechy obciążenia przekładni pracującej w projektowanej obrabiarce, np. nierównomierne obciążenie technologiczne wrzeciona frezarki (pulsujące siły skrawania), które ma największy udział w obciążeniu ostatniej przekładni. Pulsacja ta jest tłumiona przez elementy napędu i w niewielkim stopniu przenosi się na przekładnie początkowe.

Współczynnik przeciążenia dla napędów elektrycznych przyjmuje się równy 1,25, a sprawność pojedynczego stopnia przekładni w napędzie głównym wynosi około 95% (zazębienie i łożyskowanie). Nie zakłada się możliwości przeciążania silnika w obrabiarkach specjalnych i jednostkach obróbkowych obrabiarek zespołowych (poza frezarskimi), w których moc silnika napędowego została dobrana do oporów skrawania, a siły technologiczne nie wykazują pulsacji. Dla tych założeń opracowano wzory do wyznaczania wartości współczynników obliczeniowych C₀ zestawionych w tablicy 2.1.

TABLICA 2.1. Wyznaczanie obliczeniowego współczynnika obciążenia

Charakter pracy i rodzaj obrabiarki		C0
Opory skrawania stałe lub słabo zmienne, okresowe przeciążenia, pulsa-	obrabiarki ogólnego przeznaczenia z wyjątkiem frezarek	1,25 * 0,95^S
cje sił skrawania występujące sporadycznie	automaty i półautomaty tokarskie, obrabiarki specjalne, jednostki obróbkowe obrabiarek zespołowych (z wyjątkiem frezarskich)	0,95^S
Pulsujące opory skrawania, okresowe przeciążenia	frezarki uniwersalne i specjalizowane, frezarskie jednostki obróbcze obrabiarek zespołowych	1,25
S * liczba stopni przekładni między silnikiem a obliczaną parą kół zębatych.

Największy moment obrotowy mają przekładnie elementarne podczas przenoszenia małych prędkości obrotowych. Na rysunku 2.4 pokazano przykład wykresu przełożeń, na którym pogrubiono linie oznaczające przenoszenie małych prędkości obrotowych. Na wałku IV (na wrzecionie obrabiarki) w zakresie prędkości obrotowych n₁*n' moment obrotowy jest jednakowy (jednakowe siły), lecz najbardziej niekorzystne warunki pracy łożysk tocznych występują przy największych obrotach zakresu (czyli przy prędkości n').

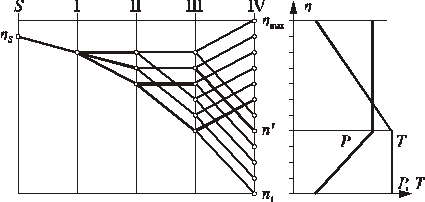
Rys. 2.4. Określanie prędkości obrotowych wałków do obliczeń kół zębatych

w reduktorze wielobiegowym

W podobny sposób na podstawie charakterystyki mechanicznej napędu określa się obciążenie obliczeniowe dla kół zębatych przekładni mechanicznych napędów bezstopniowych.

2.3. Obliczanie zębów na naciski powierzchniowe

Celem obliczeń wytrzymałościowych kół zębatych jest dobór podstawowych parametrów, tj. modułu i szerokości wieńca. Trzecim parametrem jest współczynnik przesunięcia zarysu zębów, który może być przyjęty z warunków geometrycznych, np. z przyjętej odległości osi kół.

Na rysunku 2.5 przedstawiono model geometryczny obliczania nacisków powierzchniowych (według Niemanna [4]). Stykające się ewolwentowe zarysy zębów mają środki swych krzywizn w punktach G₁ i G₂ styku linii przyporu z okręgami zasadniczymi, zatem długość odcinka G₁G₂ jest sumą promieni krzywizn stykających się zarysów. Kolejne zarysy zębów danego koła są odległe od siebie o wartość podziałki zasadniczej. Odcinek przyporu jest ograniczony okręgami wierzchołków zębów (w przypadku zarysów nie podciętych). Z takich założeń wynikają strefy współpracy:

 dwóch par zębów na odcinkach E₂B₁ i B₂E₁,

 jednoparowego zazębienia na odcinku B₁B₂.

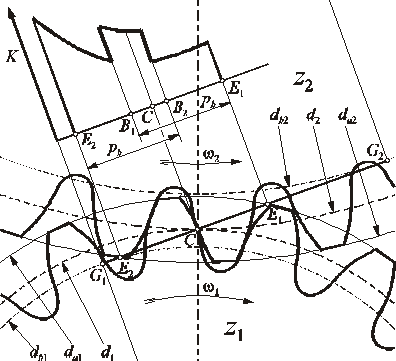
Rys. 2.5. Model geometryczny do obliczeń wytrzymałości zębów na naciski

powierzchniowe (z₁ = 18, z₂ = 36)

Jeżeli przyjmie się jako miarę nacisków wskaźnik Stribecka, to podstawową postać warunku wytrzymałościowego (przez analogię do wzoru Levisa na zginanie u podstawy zęba) można przedstawić wzorem:

, (2.13)

gdzie: K * wskaźnik krzywizny w obliczeniowym punkcie styku zębów, F₀ * siła obwodowa (styczna do okręgu podziałowego).

Na rysunku 2.5 pokazano, jak zmienia się wskaźnik krzywizny wzdłuż linii przyporu. W punktach charakterystycznych zazębienia przyjmuje on wartości:

* w punkcie B₁ początku strefy jednoparowego zazębienia:

, (2.14)

* w punkcie E₂ początku zazębienia:

. (2.15)

W punkcie E₂ siła obwodowa rozkłada się między dwie pary zębów proporcjonalnie do sztywności stykowej w punktach E₂ i B₂. Według badań Niemanna [4], znajdujących potwierdzenie u innych autorów (np. [2]), stosunek sztywności zębów stykających się w tych punktach określa przybliżony wzór:

. (2.16)

Na tej podstawie zastępczy wskaźnik krzywizny w punkcie E₂ można wyrazić zależnością:

. (2.17)

Wskaźnik zazębienia w zakresie współpracy zębów nie podciętych wyznacza się ze wzoru:

, (2.18)

w którym poszczególne człony wyznacza się z zależności:

, (2.19)

. (2.20)

W przykładach podanych na rysunkach 2.5 i 2.7 w zazębieniu zerowym (x₁ =
= x₂ = 0) dominują naprężenia w punkcie skrajnym E₂. Na skutek dużych poślizgów w tym punkcie stan ten może zmienić się po okresie docierania przekładni, gdy uzębienie przynajmniej jednego koła nie jest utwardzone. Natomiast w napędach obrabiarek, w których najczęściej oba koła są twarde, wcześniej mogą wystąpić objawy zmęczenia powierzchniowego [2].

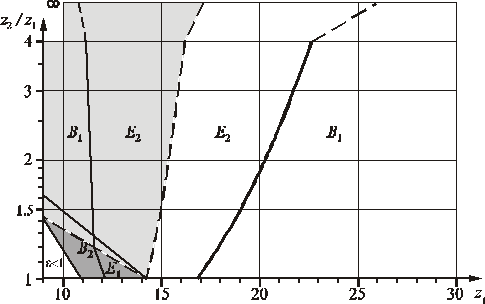
Rys. 2.6. Zakresy dominacji wskaźników krzywizn w charakterystycznych punktach zazębienia zerowego; w polach zaciemnionych odcinek przyporu jest ograniczony podcięciem zębów (w polu bardziej zaciemnionym * obu kół przekładni)

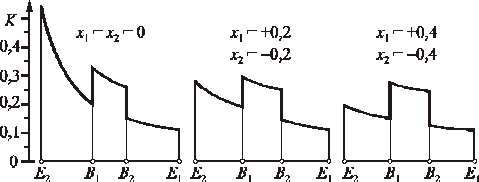
Rys. 2.7. Wskaźniki krzywizn w funkcji położenia punktów styku zębów na linii

przyporu (z₁ = 17; z₂ = 34)

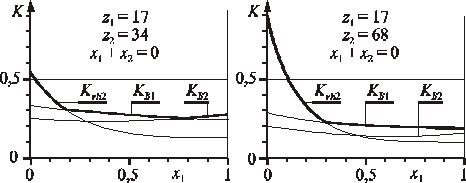
Rys. 2.8. Wpływ współczynnika przesunięcia zarysu na wskaźniki krzywizn

w charakterystycznych punktach zazębienia

Na rysunku 2.6 pokazano zakres dominacji wskaźników krzywizn w charakterystycznych punktach zazębienia zerowego (x₁ = x₂ = 0). Z przykładu podanego na rysunku 2.7 widać, że nawet niewielkie dodatnie przesunięcie zarysu małego koła zmniejsza wyraźnie wskaźnik krzywizny w punkcie E₂ i dominujący może się stać wskaźnik krzywizny w punkcie B₁. Podobne wnioski można wyciągnąć z wykresów przedstawionych na rysunku 2.8.

Współczynniki przesunięcia zarysów powinny być tak dobrane, aby przede wszystkim wyeliminować duże krzywizny zastępcze w początkowym punkcie współpracy zębów E₂. Zwiększanie współczynnika x₁ powyżej wartości, dla której K_B1 = K_vE2, prowadzi także do zmniejszenia dominującego wskaźnika krzywizny K_B1, lecz już w znacznie słabszym stopniu. Algorytm wyznaczania tego granicznego współczynnika x przedstawiono na rysunku 2.9. Algorytm ten wykorzystano w programie komputerowym do obliczeń kół zębatych. Po przyjęciu współczynnika przesunięcia zarysu x większego od granicznego (lub równego granicznemu) można przystąpić do obliczania modułu i szerokości wieńca z wykorzystaniem wskaźnika krzywizny w punkcie G_B początku jednoparowego zazębienia.

Jeżeli do wzoru (2.13) wstawi się siłę F₀ jako funkcję mocy obliczeniowej i prędkości obrotowej, to otrzymuje się zależność:

[mm³] (2.21)

lub dla napędów posuwowych, gdy dany jest moment obrotowy T₀ [N ⋅ m]:

[mm³] . (2.22)

DANE: z1, z2, Z0, ;

;

OBLICZENIE KvE i KB

OBLICZENIE KvE i KB

OBLICZENIE KvE i KB

TAK

NIE

WYNIK: x1 (wartość graniczna)

TAK

OBLICZENIE KvE i KB

NIE

Rys. 2.9. Algorytm wyznaczania granicznego współczynnika przesunięcia zarysu zębów, dla którego K_B1 = K_vE2

Iloczyn kwadratu modułu i szerokości obliczeniowej wieńca (bm²) pozwala przewidywać tę szerokość, która będzie odpowiadać przyjętemu modułowi. Na przykład, gdy wartość bm² = 100 mm³, to konstruktor łatwo obliczy, że przyjmując moduł m = 3 mm, może spodziewać się szerokości b = 11,1 mm, a dla modułu m = 2,5 mm otrzyma b = 16 mm. Szerokość tę należy jeszcze zwiększyć, aby uwzględnić współczynnik dynamiczny siły obwodowej oraz zaokrąglenie czół zębów kół zespołów przesuwnych.

Obliczona przekładnia powinna być sprawdzona na zginanie zębów u podstawy. Tok obliczeń przekładni elementarnych omówiono w rozdziale 2.5.

2.4. Obliczanie zębów na zginanie u podstawy

Wspólną cechą metod stosowanych do obliczeń zębów na zginanie u podstawy jest postać wzoru podstawowego:

. (2.23)

Współczynnik kształtu zęba q jest wyrażany jako iloczyn:

, (2.24)

w którym: q_z * współczynnik zależny od kształtu zęba, q_ * współczynnik
uwzględniający rozkład siły w zazębieniu i miejsce jej przyłożenia.

Według badań elastooptycznych Niemanna współczynnik ten można wyrazić wzorem:

, (2.25)

dającym wystarczająco dokładne wyniki, wygodnym zwłaszcza na etapie obliczeń wstępnych, gdy moduł uzębienia nie jest jeszcze określony.

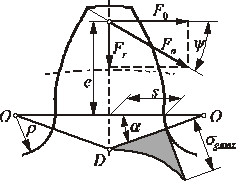
Rys. 2.10. Model geometryczny metody łamanych przekrojów [3] do wyznaczania wytężenia materiału u podstawy zęba

Na rysunku 2.10 przedstawiono model geometryczny metody łamanych przekrojów, służącej do wyznaczania wytężenia materiału u podstawy zęba. Przekrój niebezpieczny ODO ma kształt zbliżony do wyrwy pozostałej po wyłamanym zębie. Wzór na współczynnik kształtu wyprowadzony z tego modelu ma postać:

. (2.26)

Ponieważ obliczanie współczynnika q_z ze wzoru (2.26) jest bardzo uciążliwe, publikuje się wykresy [3], z których można odczytać jego wartości z dokładnością wystarczającą do obliczeń. Wykres taki przedstawiono na rysunku 2.11 (linie ciągłe).

Odczytywania wartości z wykresu nie można stosować w programach komputerowych, a interpolacja odczytu dla współczynników przesunięcia zarysu jest bardzo trudna. Wygodniejsze jest użycie wzoru przybliżonego (opracowanego przez autora):

. (2.27)

Funkcję (2.27) przedstawiono na rysunku 2.11 liniami przerywanymi. W zakresie stosowanych liczb zębów i współczynników przesunięcia zarysu błąd wartości obliczanych ze wzoru przybliżonego (2.27) nie przekracza 3,5% wartości wyznaczonych metodą łamanych przekrojów.

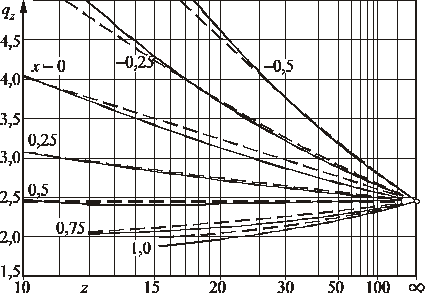
Rys. 2.11. Wykres zależności współczynnika kształtu zęba q_z od liczby zębów koła
i współczynnika przesunięcia zarysu; linie ciągłe * wartości otrzymane metodą łamanych przekrojów, linie przerywane  wartości obliczone ze wzoru (2.27)

Po podstawieniu do wzoru (2.24) zależności (2.25) i (2.27) otrzymuje się przydatną postać wzoru na współczynnik kształtu zęba:

. (2.28)

Podobna postać wzoru (2.13) na naciski powierzchniowe oraz wzoru (2.23) na zginanie u podstawy ułatwia porównanie wytrzymałości zębów na zginanie i na naciski. Po wyznaczeniu z tych wzorów minimalnej szerokości wieńca i podzieleniu wyników stronami otrzymuje się porównawczy wskaźnik wytrzymałościowy:

. (2.29)

Wartość liczby W wskazuje na to, że gdy:

W < 1 * decydujące jest obliczenie na naciski powierzchniowe,

W > 1 * decydujące jest obliczenie na zginanie zęba u podstawy.

W napędach głównych obrabiarek wskaźnik W > 1 występuje rzadko, w niektórych przypadkach kół pośrednich, w których zęby są zginane obustronnie.

2.5. Algorytm obliczeń kół zębatych

Przedstawiony algorytm dotyczy obliczeń grupy kół zębatych o zębach prostych oraz o jednakowym module i materiale.

Dobór materiału

Zestaw materiałów ujętych w programie komputerowym przedstawiono na rysunku 2.3. Na koła zębate o średnich modułach (2,5*4) najczęściej jest stosowana stal nawęglana i hartowana (np. 20H).

Rys. 2.12. Obraz na ekranie monitora podczas doboru współczynników przesunięcia zarysów kół zębatych (dane dla wiertarki z przykładu na rys. 1.12 i 1.13)

Wprowadzanie danych do obliczeń kół zębatych

Na rysunku 2.12 pokazano obraz ekranu monitora podczas wprowadzania danych do obliczeń kół zębatych. Jeżeli w skrzynce prędkości zaprojektowano koła wiązane (pośrednie), to w obu przekładniach elementarnych muszą być one oznaczone tym samym numerem. Jest to wskazówka dla programu, że tak oznaczone koło jest poddane obustronnemu zginaniu zębów.

Współczynniki przesunięcia zarysu nie muszą być podawane na tym etapie, będą bowiem ustalane osobno.

Jest obojętne, które koło: większe czy mniejsze, czynne czy bierne, będzie
oznaczone przez z₁, a które przez z₂, lecz prędkości obrotowe: największa i najmniejsza (obliczeniowa * patrz rys. 2.4) muszą odpowiadać kołu z₁. Na rysunku 2.12 rubryka z₁ dotyczy kół napędzających.

Wskaźnik odległości osi, będący sumą liczb zębów przekładni elementarnej, dla którego będzie przyjęta odległość osi, jest jednakowy dla zespołu przekładni elementarnych.

Wartość mocy przenoszonej przy obliczeniowej prędkości obrotowej należy obliczyć i przyjąć według zasad omówionych w rozdziale 2.2.

Dobór współczynników przesunięcia zarysów

Współczynniki przesunięcia zarysów w obliczanej przekładni dobiera się na podstawie własnych kryteriów i propozycji komputerowych. Współczynniki te powinny być dobrane z zakresu ograniczonego z jednej strony przez warunek dominacji krzywizny w punkcie B₁ dla danej pary kół oraz z drugiej przez zaostrzenie zęba lub nierówność x < 1 dla każdego koła przekładni (rys. 2.12). Naciśnięcie przycisku ENTER oznacza przyjęcie propozycji komputerowej, a wprowadzenie innej wartości współczynnika x jest jednoznaczne z przyjęciem do obliczeń przekładni z dominującymi krzywiznami w zazębieniu.

Obliczenie modułu

Wielkość zęba jest obliczana ze wzoru (2.21) na naciski powierzchniowe. Końcowy wynik obliczeń (szerokość wieńca) może być skorygowany przez porównawczy wskaźnik wytrzymałościowy (jeżeli W > 1). Dla kolejnych wartości modułów z szeregu Maaga są obliczane szerokości wieńców z zależności:

, (2.30)

gdzie K_d jest współczynnikiem dynamicznym, zależnym od klasy dokładności uzębienia i obliczeniowej prędkości obwodowej.

Klasę dokładności uzębienia przyjmuje się zależnie od największej prędkości obwodowej:

[m/s] , (2.31)

gdzie d [mm] jest średnicą podziałową koła zębatego obracającego się z prędkością n_max. W tablicy 2.2 przedstawiono kryterium wyboru klasy dokładności uzębienia stosowane w Fabryce Obrabiarek HCP.

TABLICA 2.2. Wybór klasy dokładności uzębienia

Prędkość obwodowa vmax [m/s]	≤ 1	> 1*2	> 2*4	> 4*8	> 8*16	> 16
Klasa dokładności KL	9	8	7	6	5	4

W zakresie prędkości (0,5 < v_max < 32) m/s zależność przedstawioną w tablicy 2.2 można ująć wzorem:

. (2.32)

Współczynnik dynamiczny (według Niemanna [4, 5]) dla prędkości obwodowych mniejszych od 7 m/s, które występują przy największych obciążeniach przekładni, jest zależny od odchyłek Δp_b podziałki zasadniczej:

. (2.33)

Na etapie obliczeń, gdy nie można jeszcze określić odchyłek podziałki zasadniczej w konkretnej przekładni, dla zakresu średnich modułów (2*5 mm) można przyjąć przybliżoną zależność dopuszczalnej odchyłki podziałki zasadniczej od klasy dokładności (opracowaną przez autora):

. (2.34)

Po podstawieniu tej zależności do wzoru (2.33) otrzymuje się:

. (2.35)

Na rysunku 2.13 z lewej strony wyszczególniono kolejne wartości modułów i odpowiadające im szerokości wieńców obliczone ze wzoru:

. (2.36)

W przekładniach wielobiegowych z kołami przesuwnymi korzystne jest przyjmowanie małej szerokości wieńców (b₀ ≈ 4m), dlatego w przykładzie wybrano moduł m = 2,5 mm, któremu odpowiada b₀ = 11,95 mm.

Rys. 2.13. Dobór modułu * na ekranie monitora kolorem wyróżniono pole danych najbardziej obciążonej przekładni * z₇/z₈  o liczbach zębów 19/49

Przyjęcie szerokości wieńców

Wyniki obliczeń kół zębatych są drukowane w postaci tablicy przedstawionej na rysunku 2.14. Oprócz omówionych wyżej parametrów tablica ta zawiera także nominalne wartości pomiaru przez kilka zębów W_n niezbędne do kontroli grubości zębów szlifowanych.

Minimalna obliczeniowa wartość szerokości wieńca, wynikająca z obliczeń na naciski powierzchniowe, jest podana w tablicy, a konstruktor powinien przyjąć szerokość rysunkową z uwzględnieniem technologii kół zębatych (np. zbyt małe szerokości wieńców prowadzą do dużych zniekształceń podczas obróbki cieplnej). Należy także powiększyć szerokość wieńca o wartość zaokrąglenia czół zębów kół przełączalnych (rys. 2.15).

Obliczenie zębów na zginanie u podstawy wymaga spełnienia warunku:

. (2.37)

Przyjętą wartość szerokości wieńca można wpisać do tablicy wyników.

Rys. 2.14. Wyniki obliczeń kół zębatych przekładni wielobiegowej

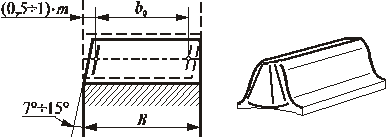
Rys. 2.15. Przykład zaokrąglonego czoła zęba

2.6. Zazębienie koła z zębatką

Zazębienie koła z listwą zębatą jest szczególnym skojarzeniem, w którym liczba zębów większego koła jest nieskończona. Z tego powodu większość wzorów stosowanych do przekładni zębatych staje się wyrażeniami nieoznaczonymi i nie może być tutaj wykorzystana.

Do obliczeń naprężeń na powierzchni zęba oraz na zginanie służą te same wzory podstawowe (2.13) i (2.23) co do zwykłych przekładni, jednakże wskaźnik zazębienia oraz wskaźniki krzywizn są wyznaczane z zależności dostosowanych do tego przypadku * zazębienia koła o z zębach z zębatką.

Wskaźnik zazębienia:

, (2.38)

wskaźnik krzywizny w punkcie B₁:

, (2.39)

a zastępczy wskaźnik krzywizny w punkcie E₂:

. (2.40)

Na rysunku 2.16 przedstawiono wykres ograniczeń współczynników przesunięcia zarysu kół zazębianych z zębatką. Ponieważ zazwyczaj projektuje się w takiej przekładni koło o małej liczbie zębów, to należy przyjąć współczynnik przesunięcia zarysu z prawej strony linii E₂B₁ lub znad tej linii, tj. z pola dominacji krzywizny w punkcie B₁. Szczególnie duże naprężenia w punkcie E₂ wystąpią w pobliżu granicy podcięcia zębów, gdzie (teoretycznie) promień krzywizny ewolwenty jest bliski zeru. Pole zębów podciętych (zaciemnione) określono dla założenia szlifowania zębów narzędziem o zarysie prostoliniowym. Górne linie na wykresie są teoretyczną (s_a = 0) i praktyczną (s_a = 0,3m) granicą zaostrzenia zęba.

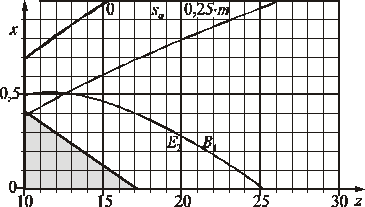
Rys. 2.16. Wykres ograniczeń współczynnika przesunięcia zarysu koła zębatego współpracującego z zębatką (zaciemniono pole zębów podciętych)

Zazębienie koła z zębatką występuje w przekładniach wolnobieżnych (np. wysuw wrzeciona wiertarki), gdzie praktycznie nie nastąpi zmęczenie materiału.

Do obliczeń wytrzymałościowych można zatem przyjąć naprężenia dopuszczalne na powierzchni zęba dwukrotnie większe, niż to wynika ze wzoru (2.9), a naprężenia na zginanie zębów zwiększyć o 60% względem dopuszczalnych naprężeń zmęczeniowych (rys. 2.3).

Klasa dokładności wykonania przekładni zębatkowej zależy nie od prędkości obwodowej (małej), lecz od przeznaczenia przekładni. Zazwyczaj przyjmuje się dla kół utwardzonych i szlifowanych ekonomiczną klasę dokładności (6*8).

Obliczenia wytrzymałościowe zazębienia koła z zębatką sprowadzają się najczęściej do sprawdzenia naprężeń w zaprojektowanej przekładni.

36

2. Obliczanie kół zębatych

27

2.1. Własności materiałów stosowanych na koła zębate

29

2.2. Obciążenie obliczeniowe przekładni elementarnej

35

2.3. Obliczanie zębów na naciski powierzchniowe

37

2.4. Obliczanie zębów na zginanie u podstawy

43

2.5. Algorytm obliczeń kół zębatych

45

2.6. Zazębienie koła z zębatką

---