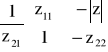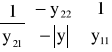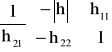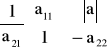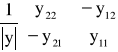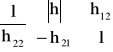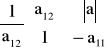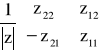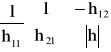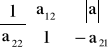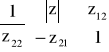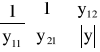Rozdział 4

Czwórniki

4.1. Równania i parametry czwórników - pojęcia podstawowe

4.1.1. Podstawowe określenia

Czwórniki to obwody elektryczne mające dostępne cztery zaciski: zaciski (pierwotne) wejściowe (oznaczone 1, 1', Rys. IV.1) oraz dwa zaciski (wtórne) wyjściowe - (oznaczone 2, 2'). Jeśli nie zawierają źródeł energii to nazywane są pasywnymi. Prąd i₁ oraz napięcie u₁ są parametrami wejściowymi, a prąd i₂ i napięcie u₂ - wyjściowymi.

Rys. IV.1. Czwórnik elektryczny

Przykładem czwórników pasywnych są dwuprzewodowe linie przesyłowe, transformatory itp., które można przedstawiać w postaci czwórników typu Γ, T, Π lub X. Nazwy te wynikają z połączeń elementów czwórnika do odpowiednich liter.

Rys. IV.2. Czwórniki typu: a) Γ; b) T, c) Π, d) X

4.1.2. Równania czwórnika pasywnego

Równanie łańcuchowe

Równanie zwane łańcuchowym przedstawia się w postaci macierzowej,

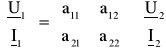
Macierz kwadratowa [a] czwórnika nazywa się macierzą łańcuchową, lub typu „a”. Jej elementy wyznacza się, rozpatrując stan jałowy
oraz stan zwarcia
czwórnika, a mianowicie

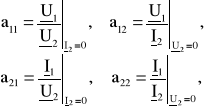
Połączenie łańcuchowe

Połączenie łańcuchowe czwórników to takie, w którym zaciski wyjściowe jednego czwórnika dołączone są do zacisków wejściowych czwórnika następnego. Poniższy rysunek przedstawia połączenie łańcuchowe trzech czwórników

Rys. IV.3. Połączenie łańcuchowe trzech czwórników

Dla powyższego połączenia obowiązują równania:

,
,
,

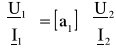
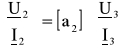
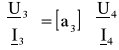
skąd otrzymuje się macierz łańcuchową zastępczą dla połączenia łańcuchowego

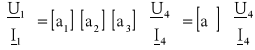
Równanie impedancyjne

Równanie to można przedstawić w postaci macierzowej następująco:

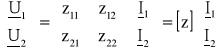
Współczynniki macierzy [z] zwanej impedancyjną, oblicza się rozpatrując stan jałowy przy zasilaniu strony pierwotnej
oraz stan jałowy przy zasilaniu strony wtórnej
:

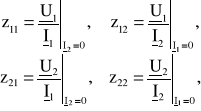
Równanie admitancyjne

Równanie to można przedstawić w postaci macierzowej następująco:

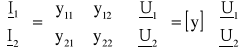
Elementy macierzy admitancyjnej [y] wyznacza się, rozpatrując stan zwarcia strony wyjściowej
oraz strony wejściowej
czwórnika:

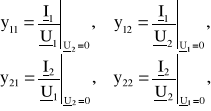
W/w elementy y mają wymiar admitancji. Z tego powodu macierz admitancyjną nazywa się macierzą „y”.

Równanie mieszane

Czasami do opisu czwórników stosuje macierz mieszaną [h]. Elementy tej macierzy określa się, rozpatrując stan zwarcia strony wyjściowej (U₂=0) oraz stan jałowy strony wejściowej (I₁=0), a mianowicie

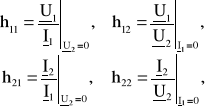
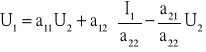
Wówczas równanie mieszane dla czwórnika można zapisać następująco

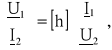
gdzie macierz kwadratowa [h] może być obliczona na podstawie znajomości parametrów macierzy łańcuchowej:

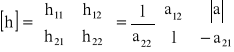
4.1.3. Zależności między parametrami macierzy [a] [z] [y] [h]

Często podawane są parametry jednej macierzy czwórnika, należy określić inne parametry. Wówczas korzysta się z równań definicyjnych lub (jak w przypadku macierzy [z] oraz [y]) oblicza się macierz odwrotne
oraz
. W większości przypadków należy wyznaczyć wyznaczniki
,
,
,
, macierzy czwórnika.

	a	z	y	h
a
z
y
h

4.1.4. Przekładnia napięciowa, prądowa i mocy

Przekładnia napięciową i prądowa czwórnika zdefiniowane są jako ilorazy wartości zespolonych napięć U₁/U₂ i prądów I₁/1₂ . W przypadku obciążenia falowego czwórnika symetrycznego przekładnie: napięciowa i prądowa czwórnika są sobie równe.

Przekładnią mocy czwórnika nazywamy iloraz S₁/S₂ mocy zespolonych na wejściu i na wyjściu czwórnika.

156

2

2'

1

1'

[a₃]

[a₂]

[a₁]

---