Rozdział 3

Obwody zawierające cewki magnetycznie sprzężone

3.1. Analiza obwodów ze sprzężeniami magnetycznymi - wstęp

teoretyczny

3.1.1. Dwie cewki magnetycznie sprzężone

Napięcia indukowane w cewkach 1, 2, pod wpływem zmian wartości chwilowych prądów i₁, i₂ , wyrażają się wzorami

gdzie L₁ oraz L₂ są indukcyjnościami własnymi cewek. Opisywane zjawisko nosi nazwę indukcji własnej.

Rys. III.1. Dwie cewki magnetycznie sprzężone

Jeżeli część strumienia wytworzonego przez prąd cewki 1 przenika drugą cewkę, to wartość chwilowa siły elektromotorycznej (sem.) w cewce 2 wyraża się wzorem:

Podobnie można wyrazić sem. w cewce 1 indukowaną przez część strumienia wytworzonego zmianami prądu cewki 2

W powyższych wzorach M jest indukcyjnością wzajemną cewek magnetycznie sprzężonych, a omawiane zjawisko nazywa się indukcją wzajemną.

W celu ułatwienia analizy układów magnetycznie sprzężonych, zaciski cewek zwane jednoimiennymi oznacza się za pomocą kropek, gwiazdek itp.. Jeżeli występuje sumowanie strumieni wytworzonych przez prądy jednocześnie dopływające do pewnych zacisków cewek, (lub odpływające od nich), to zaciski te nazywamy zaciskami jednoimiennymi. Obydwa te zaciski można nazwać „początkami” albo „końcami” tych cewek. Jeżeli dla tych samych warunków dotyczących prądów w/w strumienie się odejmują, to zaciski te nazywamy różnoimiennymi.

Jeżeli do obydwu „początków” cewek prądy dopływają lub jednocześnie odpływają, to indukcyjność wzajemna tych cewek jest dodatnia (Rys. III.2a). Jeżeli w jednej cewce prąd dopływa do jej „początku”, zaś w drugiej cewce prąd odpływa od jej „początku”, to indukcyjność wzajemna jest ujemna (Rys. III.2b).

a) b)

Rys. III.2. Przypadki ilustrujące znak indukcyjności wzajemnej

Omawiane przypadki przedstawione są schematycznie na Rys. III.2, gdzie „początki” cewek magnetycznie sprzężonych oznaczone są za pomocą gwiazdek.

Sprzężenie magnetyczne dwóch cewek charakteryzuje współczynnik sprzężenia, którego wartość zawiera się w granicach 0 ≤ k ≤ 1.

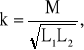
Zwrot prądu indukowanego pod wpływem sem. e indukcji wzajemnej można wyznaczyć na podstawie zasady Lenza, która głosi, że prąd ten wytwarza pole magnetyczne przeciwdziałające zmianie strumienia magnetycznego, która powoduje indukowanie się tej sem.

3.1.2. Połączenie szeregowe i równoległe cewek magnetycznie sprzężonych

Połączenie szeregowe

Rys. III.3. Połączenie szeregowe zgodne Rys. III.4. Połączenie szeregowe przeciwne

Na powyższych schematach obwodów przedstawiono połączenie szeregowe cewek magnetycznie sprzężonych. Jeżeli R₁ i R₂ oznaczają rezystancje cewek 1, 2, to na podstawie II prawa Kirchhoffa (II PK), dla pierwszego schematu (Rys. III.3), można napisać równanie:

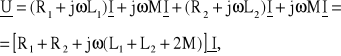
przy czym jωMI jest napięciem indukowanym w każdej cewce w wyniku zjawiska indukcji wzajemnej. Jest to połączenie szeregowe zgodne cewek magnetycznie sprzężonych.

Na drugim schemacie połączeń (Rys. III.4.) prąd I dopływający do „początku” (oznaczonego gwiazdką) cewki 1, jest równocześnie prądem odpływającym od „początku" cewki 2, wobec czego indukcyjność wzajemna obydwu cewek jest ujemna (-M). Dlatego też w powyższym równaniu należy uwzględnić jej znak. Jest to połączenie szeregowe przeciwne cewek.

Impedancja dla szeregowego połączenia dwóch cewek wyraża się wzorem:

gdzie znak (+) dotyczy połączenia zgodnego, a znak (-) połączenia przeciwnego cewek.

Połączenie równoległe

a) b)

Rys. III.5 Połączenie równoległe cewek magnetycznie sprzężonych:

a) zgodne b) przeciwne

Na powyższych schematach obwodów przedstawiono połączenie równoległe dwóch cewek magnetycznie sprzężonych. Dla połączenia zgodnego (Rys. III.5a), uwzględniając indukcyjność wzajemną (+M) cewek można napisać:

Po wyznaczeniu prądów I₁, I₂ , i oznaczeniu poszczególnych impedancji

Można wyznaczyć prąd dopływający do połączenia:

Dla połączenia przeciwnego cewek (Rys. III.5b), po uwzględnieniu znaku indukcyjności wzajemnej cewek (-M), zmianie ulega jedynie znak przy
w liczniku powyższego równania, z którego łatwo wyznaczyć impedancję zastępczą układu

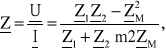
przy czym znak (-) w mianowniku dotyczy połączenia zgodnego.

3.1.3. Zastępowanie układu ze sprzężeniem magnetycznym - układem bez sprzężenia

Dla układu, w którym gałęzie zawierające elementy sprzężone magnetycznie zbiegają się w jednym wspólnym węźle, można wyróżnić dwa przypadki:

• dwa elementy sprzężone mają jednakowo usytuowane zaciski jednoimienne względem węzła;

• dwa elementy sprzężone mają przeciwnie usytuowane zaciski jednoimienne względem węzła.

W pierwszym przypadku (Rys. III.6a) zaciski jednoimienne spotykają się we wspólnym węźle. Dla tego układu można zapisać następujące równania

a) b)

Rys. III.6. Eliminacja sprzężeń magnetycznych, cewki dołączone do węzła zaciskami jednoimiennymi: a) obwód wyjściowy ze sprzężeniem; b) obwód zastępczy bez sprzężenia

W pierwszym równaniu eliminujemy prąd
podstawiając
, a w drugim równaniu eliminujemy prąd
podstawiając
. W wyniku otrzymamy

Powyższym równaniom odpowiada schemat zastępczy pokazany na Rys. III.6b. Schemat ten jest schematem zastępczym układu z Rys. III.6a. W wyniku przekształceń obwód elektryczny zawierający elementy sprzężone magnetycznie zastąpiliśmy schematem zastępczym, który nie zawiera sprzężeń.

Rozważmy jeszcze drugi przypadek przedstawiony na Rys. III.7a. Przy takim połączeniu elementów ze sprzężeniami napiszemy równania

W pierwszym równaniu eliminujemy prąd
, a w drugim prąd
. W wyniku otrzymamy

Powyższym równaniom odpowiada schemat zastępczy z Rys. III.7b.

a) b)

Rys. III.7. Eliminacja sprzężeń magnetycznych, cewki dołączone do węzła zaciskami różnoimiennymi: a) obwód wyjściowy ze sprzężeniem; b) obwód zastępczy bez sprzężenia

3.1.4. Rozwiązywanie obwodów prądu sinusoidalnego zawierających elementy sprzężone magnetycznie

Obwody magnetyczne, zawierające elementy sprzężone magnetycznie można obliczyć stosując pierwsze i drugie prawo Kirchhoffa lub inne metody wykorzystywane do analizy obwodów elektrycznych. Jednakże, niektóre z nich, jak np. metoda napięć węzłowych są niezbyt przydatne. Należy pamiętać, że znaki wyrażeń zawierających indukcyjności wzajemne zależą od zwrotów prądów względem zacisków jednoimiennych.

Rozwiązywanie obwodów ze sprzężeniami z wykorzystaniem metody prądów oczkowych przebiega jak w przypadku obwodu bez sprzężeń. Należy tylko nieco inaczej wyznaczyć impedancje własne i wzajemne oczek. Rozróżnia się dwa przypadki:

(a) Jeśli istnieją sprzężenia pomiędzy elementami należącymi do tego samego oczka, to w impedancji własnej
danego oczka wystąpi (ze znakiem + lub -) podwojona wartość impedancji wzajemnej,

(b) Jeśli brak jest sprzężeń pomiędzy elementami należącymi do tego samego oczka, to impedancja własna jest obliczana, jak w obwodzie bez sprzężeń.

W wyrażeniu określającym impedancję wzajemną oczek występują nie tylko impedancje gałęzi wspólnej sąsiednich oczek, lecz również impedancje indukcyjności wzajemnej. Ich znak zależy od zwrotów prądów oczkowych względem zacisków jednoimiennych.

Tworzenie równań obwodów ze sprzężeniami magnetycznymi można wyjaśnić na przykładzie transformatora. Dla prostoty analizy przedstawiono transformator powietrzny.

Rys. III.8. Schemat transformatora powietrznego.

Transformator jest zbudowany z dwóch lub większej liczby uzwojeń sprzężonych magnetycznie. W zależności od ich liczby rozróżnia się transformatory dwuuzwojeniowe i wielouzwojeniowe. Przekładnia zwojowa i napięciowa transformatora wyrażają się wzorami:

,

gdzie N₁ i N₂ są liczbami zwojów uzwojenia pierwotnego i wtórnego, a U₁₀ i U₂₀ są wartościami napięć w stanie jałowym (bez obciążenia).

Uwzględniając rezystancje R₁ i R₂ i indukcyjności własne L₁ i L₂ uzwojeń, na Rys. III.8 przedstawiono schemat sprzężonych magnetycznie uzwojeń transformatora dwuuzwojeniowego. Impedancję obciążenia oznaczono przez Z₀. Równanie napięciowe obwodu zasilanego (pierwotnego) ma postać

(3.1)

Znak minus przy indukcyjności wzajemnej wynika z faktu, że prądy I₁ oraz I₂ mają różne zwroty względem zacisków jednoimiennych. W obwodzie wtórnym napięcie indukowane jest równe spadkom napięć na impedancji uzwojenia wtórnego i impedancji obciążenia

(3.2)

Dla stworzenia wykresu wektorowego prądów i napięć transformatora można założyć najczęściej spotykany przypadek rezystancyjno- indukcyjnego obciążenia Z₀ = R₀ +jωL₀. Wówczas w fazie z wektorem prądu I₂ (Rys. III.9) jest wektor napięcia R₀I₂. Natomiast wektor napięcia jωL₀I₂ na reaktancji odbiornika jest prostopadły do w/w wektora prądu I₂. Podobnie, wektor napięcia R₂I₂ na rezystancji uzwojenia wtórnego jest zgodny w fazie ze zwrotem wektora prądu I₂, a wektor jωL₂I₂ , na indukcyjności własnej uzwojenia wtórnego, wyprzedza wektor prądu I₂ o kąt π/2. W/w suma napięć zgodnie z równaniem (3.2) jest równa napięciu jωMI₁ na indukcyjności wzajemnej, które wyprzedza o kąt π/2 wektor prądu I₁ .

Znając kierunek prądu I₁ można wykreślić napięcia R₁ I₁ na rezystancji i reaktancji jωL₁ I₁, obwodu pierwotnego. Zgodnie z równaniem (3.1) od sumy w/w wektorów należy odjąć napięcie indukcji wzajemnej jωMI₂, które opóźnia się względem prądu I₂ o kąt fazowy π/2. Suma tych napięć daje napięcie U₁ strony pierwotnej. W podobny sposób można wykonać wykresy dla transformatora nieobciążonego i w stanie zwarcia.

Rys. III.9. Prądy i napięcia transformatora powietrznego przy obciążeniu czynno-indukcyjnym.

Aby usunąć sprzężenia magnetyczne i zbudować schemat zastępczy transformatora, do równania obwodu pierwotnego dodaje i odejmuje się wyrażenie jωMI₁, a do drugiego równania jωMI₂. Po przekształceniu otrzymuje się

Oznaczając różnicę prądu pierwotnego i wtórnego jako I = I₁ - I₂ otrzymuje się

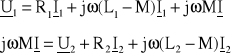
Powyższym równaniom odpowiada schemat zastępczy przedstawiony na Rys. III.10.

Rys. III.10. Schemat zastępczy (w postaci czwórnika) dla transformatora powietrznego.

Aby wyznaczyć impedancje zastępcze transformatora najlepiej posłużyć się schematem zastępczym w postaci dwójnika. W celu uproszczenia zapisu wprowadza się następujące oznaczenia: Z₁₁ = R₁ + jωL₁ = R₁₁ + jX₁₁ - impedancja własna uzwojenia pierwotnego; Z₂₂ = R₂ + jωL₂ + Z₀ = R₂₂ + jX₂₂ - impedancja własna i obciążenia uzw. wtórnego; Z_M = jωM = jX_M - impedancja indukcji wzajemnej.

Wówczas równania napięciowe można zapisać jako:

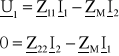
Z powyższego można określić napięcie wejściowe;

,

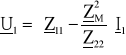
a następnie impedancję wejściową transformatora Z_we.

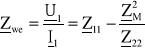
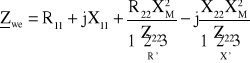
Równaniu odpowiada schemat zastępczy w postaci dwójnika, jak na Rys. III.11.

Rys. III.11. Schemat zastępczy transformatora powietrznego w postaci dwójnika.

126

M

L₁

L₂

1

2

i₁

i₂

u₁

u₂

*

+M

i₂

i₁

-M

i₂

i₁

U₁

R₀I₂

R₂I₂

I₁

I₂

R₁I₁

jωL₁I₁

jωL₀I₂

jωMI₁

jωL₂I₂

-jωMI₂

*

*

I₁

R₁₁

R'

X₁₁

X'

U₁

I₁

I₂

I

L₁-M

L₂-M

M

R₁

R₂

Z₀

U₂

U₁

M

-M

I

U

R₁

R₂

* L₁

L₂ *

+M

I

U

R₁

R₂

* L₁

* L₂

U

I₁

I₂

I

R₁

R₂

L₁

L₂

+

U

I₁

I₂

I

R₁

R₂

L₁

L₂

-M

*

*

*

*

*

*

*

Z₀

M

R₁

R₂

L₂

L₁

U₂

U₁

I₂

I₁

---