Prognozowanie Przewidywanie - to wnioskowanie o zdarzeniach nie znanych na podstawie zdarzeń znanych.
Przewidywanie przyszłości nazywamy wnioskowanie o zdarzeniach które zajdą w czasie późniejszym niż czas przewidywania na podstawie informacji o przeszłości i teraźniejszości.
Prognozowanie to racjonalne naukowe przewidywanie przyszłych zdarzeń.
Jeśli przesłanki i tok rozumowania są oparte na doświadczeniu bez użycia reguł nauki mamy doczynienia z rozumowaniem zdroworozsądkowym.
Na proces prognozowania składają się:
Poznawanie przeszłości (gromadzenia informacji).
Diagnozowanie.
Przenoszenie informacji z przeszłości w przyszłość.
Właściwości prognozy
Jest formułowana z wykorzystaniem dorobku nauki.
Jest stwierdzeniem odnoszącym się do określonej przyszłości.
Jest stwierdzeniem weryfikowanym empirycznie.
Nie jest stwierdzeniem stonowanym ale akceptowalnym.
Głównym celem prognozowania społecznego jest wspomaganie procesów decyzyjnych. Stąd główne funkcje prognozowania to:
Ilościowe (stan zmiennej wyrażony jest liczbą)
punktowe,
podziałowe.
Jakościowe (prognozowanym zdarzeniem jest stan zmiennej niemierzalnej)
Ze względu na te zmiany zachodzące w zjawisku prognozy dzielimy na:
Krótkookresowe - gdy zmiany wartości zmiennej zachodzą zgodnie z odkrytą prawidłowością.
Średniookresowe - zachodzą zmiany ilościowe i śladowe zmiany jakościowe.
Długookresowe - dotyczą dłuższych odcinków czasu - zachodzą zmiany ilościowe i poważne zmiany jakościowe.
Prognozowania dokonuje na podstawie danych , które coś wnoszą do zjawiska. Dane te powinny spełniać następujące kryteria:
prawdziwość,
jednoznaczność,
identyfikacja zjawiska przez zmienną,
kompletność,
aktualność danych dla przyszłości,
rozsądny koszt gromadzenia i opracowywania,
porównywalność danych.
Informacje dotyczące zmiennych (cech) są powtarzalne i zwykle zapisywane są w postaci szeregów czasowych.
Rodzaje szeregów:
jednowymiarowy szereg czasowy {Yi } = 1,...,n
wielowymiarowy szereg czasowy - zbiór szeregów dla zmiennych Yi = Y2,...,Yn
jednowymiarowy szereg przekrojowy - ciąg stanów zmiennych „Y”, z których każdy odnosi się do tego samego okresu.
Wielowymiarowy szereg przekrojowy.
Szereg przekrojowo-czasowy.
Metody analizy i prognozowania
metod eksploatacji trendu,
metody modelowania przyczynowo-skutkowego:
metody matematyczno-ekonomiczne,
modele behawiorystyczne - odwzorowujące zachowanie badanego systemu, np.: symulacje.
Metody analogowe - prognozowanie zjawiska na podstawie informacji o zjawiskach podobnych.
Metody heurystyczne - wykorzystywanie opinii ekspertów, opartej na intuicji i doświadczeniu.
Scenariusze - kombinacja różnych metod, zwykle ma charakter opiniowy.
Etapy PROGNOZOWANIA
Sformułowanie zadania.
Podanie przesłanek prognostycznych i zebranie danych.
Wybór metody prognozowania.
Wyznaczanie prognozy.
Ocena dokładności prognozy.
Ustalanie horyzontu prognozy.
Weryfikacja prognozy.
Ogólnie postać modelu czasowego można zapisać:
yi = f (t, yt-1, ..., yt-p, yt-1*,..., yt-p, ∑t)
* - prognoza
t - przyszłość
Dla modelu addytywnego, jeśli jedyną zmienną objaśniającą jest czas to:
Yt = f(t) + g(t) + h(t) + ∑t
Gdzie kolejne elementy to:
funkcja tendencji rozwojowej trendu,
funkcja charakteryzująca wahania sezonu,
funkcja charakteryzujący wahania cykliczne,
funkcja charakteryzująca wahania przypadkowe.
Symulacja oznacza wykorzystanie zestawu różnicowych technik badawczych, polegających na wprawieniu w ruch modelu naśladującego zachowanie danego systemu. Mamy możliwość obserwacji zjawisk gospodarczych i eksperymentowania z nimi. Budowa i uruchamianie modelu symulacyjnego pozwala na obserwację dynamiki modelowego systemu w warunkach kontrolowanych przez eksperymentora. Możemy zmieniać warunki, aby zbadać zasobność badanych hipotez.
Symulacja stwarza laboratorium, w którym możemy analizować problemy ekonomiczne w sposób w jaki w rzeczywistości nigdy tego nie moglibyśmy zrobić. Prognozowanie i symulacja wzajemnie się uzupełniają i wspierają (wyznaczamy prognozę przez symulację lub wykorzystujemy w symulacji prognozy zmiennych empirycznych otrzymanych na podstawie np.: szeregów czasowych).
Symulację dzielimy na:
Deterministyczną - proces numerycznego rozwiązywania modelu w celu wyznaczenia trajektorii zmiennych endogenicznych.
Stochastyczną - gdy uwzględniamy źródła niepewności w zachowaniu modelowego systemu.
Modele i metody prognozowania
Metody naiwne - oparte na bardzo prostych przesłankach dotyczących przeszłości:
y*t = yt-1 prognoza jest równo prognozie z okresu poprzednio zaobserwowanego,
y*t = yt1 + (yt-1 - yt-2) - gdy w szeregu występuje tendencja rozwojowa, możny przyjąć, że prognoza na okres „t” jest równa wartości rzeczywistej z okresu „t-1” powiększonej o przyrost wartości „t-1” w stosunku do okresu „t-2”,
y*t = (1+c)y-1 - zmiana o c%,
![]()
![]()
prognozowanie jest równe wartości z okresu t-1 powiększonej o średni przyrost wartości zmiennej w dostępnym materiale statystycznym.
y*t = yt-k - w przypadku występujących w szeregu czasowym wahań sezonowych.
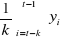
Metody średniej ruchomej - używamy do wygładzania szeregu czasowego oraz do prognozowania:
gdzie, „k” stała wygładzenia.
![]()
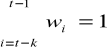
wi - przyjęte wagi, liczby nieujemne.
Metody wygładzania wykładniczego:
Prosta metoda wygładzania wykładniczego (m. Browna) - stosujemy w przypadkach występowania w szeregu czasowym prawie stałego poziomu zmiennej obserwowanej oraz wahań przypadkowych.
![]()
y*t = αt-1 + (1 + α)y*t-1, gdzie α є [0,1] - stała wygładzania, inaczej:
y*t = α yt-1 + α (1 - α)yt-2 + α (1 - α)2 yt-3 + α (1 - α)y3 t-1 +...+ (1 - α)t-1 y*t
Metoda liniowa HOLTA - gdy występuje tendencja rozwojowa i wahania przypadkowe,
Metoda WINTERA - gdy występuje tendencja rozwojowa, wahania sezonowe i wahania przypadkowe.
Trafność prognoz otrzymanych na podstawie metod naiwnych jest na ogół niska. Ich ocenę przeprowadza się na podstawie błędów ex post:
bezwzględny błąd prognozy,
qt = yt - yt*, t = n+1,..., T
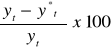
względny błąd prognozy:
średni względny błąd prognozy ex post:
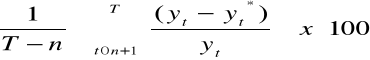
gdzie t = n+1,...T
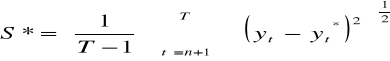
średni kwadratowy błąd prognozy ex post:współczynnik janusowy:
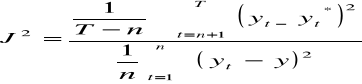
jeśli J2 ≤ 1 wówczas model uznajemy za dobry
Metoda wygładzania wykładniczego HOLTA
Metodę tę stosujemy w wypadku, gdy zjawisko ma wyrażony trend i nie ma wahań sezonowych. Przyjmujemy dwa parametry 0< α, β <1, a następnie postępuje wg wzoru:
F1 = y1; T1 = 0
y* = F1 + T1 = y(1)
wartości teoretycznej dla pozostałych okresów (dla t = 1, 2, ... u) wyznaczoną zgodnie ze wzorem:
y*t = Ft + Tt, gdzie:
Ft = α yt-1 + (1 + α)(Ft-1 + Tt-1) = αyt-1 + (1 - α)yt-1* = yt-1* + αqt-1;
Tt = β (Ft - Ft-1) + (1 + β) Tt-1
Prognoza na okres T>n dokonujemy zgodnie ze wzorem:
y*t = yt-1 + Tn stąd
yT* = yn* (T - n) Tn
MODEL LINIOWY HOLTA
t |
yt |
Ft |
Tt |
y*t |
qt |
wt |
qt^2 |
IwtI |
y*t-yśr |
(yt-yśr)^2 |
|
|
|
|
|
|
|
|
|
|
|
yśr = 16,86; α = 0,20; β = 0,80; J2 = 0,10; S* = 1,52; q = 7,7%
Ft = y*t-1 + αqt-1
F1 = y*t-1 + 0,2qt-1
Tt = β (Ft - Ft - 1) + (1 - β) Tt-1
y*T = y*T + (T - 14) T14
MODELE TENDENCJI ROZWOJOWEJ
Modele analityczne.
Trend liniowy yt = α + βt + ξt,
Trend wykładniczy yt = e α + βt + ξt, yt = αβt,
Wielomian stopnia 2: yt = α0 + α1t + α2t2 + ξt, α2 > 0,
Trend postępowy yt = αtβ, β>1,
Funkcje o malejącej stopie wzrostu:
Logarytmiczna yt = α + βlnt + ξt, β>0 (t´ = lnt)
Potęgowa yt = αtβ, 1> α >0, (α´=lnα)
yt = lnyt, (t´=lnt)
MODEL LINIOWO - ODWROTNOŚCI OWY
yt =α + βt-1 + ξt, β>0
Jeżeli wartość zmiennej badanej w danym okresie zależy od wartości tej zmiennej z okresów poprzednich wówczas stosujemy modele atoregresyjne:
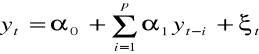
yt = f (yt-1, yt-2, ..., pt-p, ξ), na ogół przyjmujemy że,
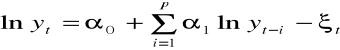
gdzie p - rząd atoregresji, lub
TREND LINIOWY
Jeżeli mamy postać liniową modelu tendencji rozwojowej
Yi = α + βti + ξi
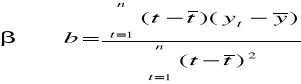
Do oszacowania parametrów zwykle stosuje się MNK
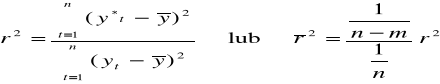
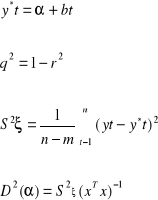
Po wyborze postaci funkcji trendu oraz wyznaczenia ocen parametrów oceniamy jakość modelu:
![]()
Zwykle stosując model trendu liniowego
Na początek dokonujemy przenumerowania okresów ti → ti´, w ten sposób, aby
![]()
Przykład
ti |
ti´ |
|
ti |
ti´ |
|
ti |
ti´ |
1 |
-2 |
|
1 |
-5 |
|
1 |
-3 |
2 |
-1 |
|
2 |
-3 |
|
2 |
-2 |
3 |
0 |
|
3 |
-1 |
|
3 |
-1 |
4 |
1 |
|
4 |
1 |
|
5 |
1 |
5 |
2 |
|
5 |
3 |
|
6 |
2 |
|
|
|
6 |
5 |
|
7 |
3 |
„n” nieparzyste „n” parzyste okresy nie są kolejne
![]()
Jeżeli w szeregu czasowym dane nie pochodzą z okresów kolejnych wówczas przenumerowanie okresów dokonujemy zgodnie ze wzorem:
![]()
Gdzie „l” jest najmniejszą liczbą naturalną, taką, że wszystkie ti są całkowite. Jeśli dokonujemy przenumerowania okresów wówczas otrzymujemy model:
Jeśli oszacowanie parametru α oznaczymy przez „a”, natomiast oszacowanie parametru β przez „b”, wówczas powstanie MNK zależności:
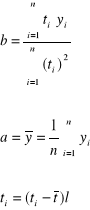
![]()
Jeżeli chcemy dokonać prognozy punktowej na okres T > n, wartości zmiennej „y”, wówczas wyznaczamy odpowiedni okres „T”, a następnie wykorzystujemy wzór:
Chcąc oszacować średni błąd prognozy posługujemy się wzorami:
Mając średni błąd prognozy możemy teraz zbudować przedział ufności dla prognozy, analogicznie jak podano wcześniej, a zatem:
![]()
Uα jest wartością krytyczną odczytaną z tablic dystrybuanty rozkładu t - studenta, jeśli n-2<30, lub rozkładu normalnego, jeśli n-2>30.
Chcącą rozbudować jakość zastosowanego modelu obliczamy współczynnik zbieżności „ρ2” lub współczynnik determinacji „r2”.
PRZYKŁAD (na kartce)
MODEL ADAPTACYJNY. TREND SPEŁZAJĄCY
Wnioskowanie stosujące klasyczne modele tendencji rozwojowej wiąże się ze znacznym ryzykiem, iż prognozy będą oparte na modelu zdezaktualizowanym, a więc takim, którego postać analityczny lub parametry strukturalne zmieniły się. spowoduje to, że model taki mniej dokładnie odzwierciedla rzeczywistość, czego następstwem są większe błędy prognozy. Zbudowany zatem model adaptacyjny, przy którym odrzuca się krępujące założenie, przy budowie analitycznych modeli tendencji rozwojowej, o nie zmienności mechanizmu rozwojowego badanych zjawisk. Duża elastyczność modelu adaptacyjnego, umożliwiająca ujęcie nieregularnych zmian w składowych szeregu czasowego, powoduje, że jest to narzędzie wygodne do budowy prognoz krótkookresowych. Klasa modelu adaptacyjnego jest szeroka. Jeden z nich to model trendu pełzającego, p procedurze budowy (HELLWING 1961).
Dla danego szeregu czasu yi, ...,yn oraz arbitualnie ustalana stała wygładzenia k<n szacuje się na podstawie kolejnych fragmentów szeregu.
y1,...,yk
y2,...,yk+1
yn-k+1,...,yn
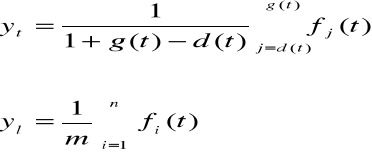
łącząc kolejne punkty (t, yśr) odcinkami liniowymi, otrzymuje się wykres tzw. rozwojowy szeregu czasowego w postaci funkcji segmentowej, zwanej trendem pełzającym.
W celu eksploatacji trendu w przyszłości należy użyć algorytmu, zwanego metodą wag harmonicznych:
Oblicza się przyrost funkcji trendu:
![]()
Określa się średnią przyrostów.
![]()
gdzie, cnt+1 - wagi harmoniczne, realizujące postulat postarzenia informacji.
Nadawane są one przyrostom w taki sposób, aby najstarsze miały najmniejsze znaczenie, najnowsze zaś największe. Wagi te są liczbami dodatnimi z przedziału (0,1) o sumie równej wartości i o konstrukcji:
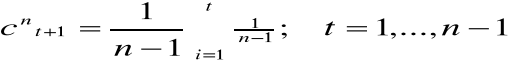
wyznaczane są odchylenia standardowe przyrostów trendu pełzającego, ważonych wagami harmonicznymi:
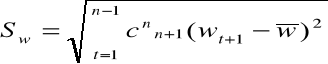
przez „doklejenie” do ostatniego punktu trendu pełzającego (n, ўn) prostej o nachyleniu”ŵ” dokonuje się ekstrapolacji trendu. Prognozę punktową na moment, okres „T” wyznacza się wg wzoru:
![]()
Przykład
ti |
yi |
y*(1) |
y*(2) |
y*(3) |
y*(4) |
y1 |
wi |
Ci |
Wici |
1 |
2 |
2 |
|
|
|
2,000 |
|
|
|
2 |
3 |
3 |
3 |
|
|
3,000 |
1,00, |
0,020 |
0,020 |
3 |
5 |
4 |
4 |
4 |
|
4,000 |
1,000 |
0,044 |
0,044 |
4 |
3 |
5 |
5 |
5 |
4,4 |
4,850 |
0,850 |
0,073 |
0,062 |
5 |
7 |
6 |
6 |
6 |
5,5 |
5,875 |
1,025 |
0,109 |
0,111 |
6 |
7 |
|
7 |
7 |
6,6 |
6,867 |
0,992 |
0,156 |
0,155 |
7 |
8 |
|
|
8 |
7,7 |
7,850 |
0,983 |
0,228 |
0,224 |
8 |
8 |
|
|
|
8,8 |
8,800 |
0,950 |
0,370 |
0,352 |
∑ |
43 |
20 |
25 |
30 |
33 |
43,24 |
6,8 |
1 |
0,968 |
Stała wygładzania - 5
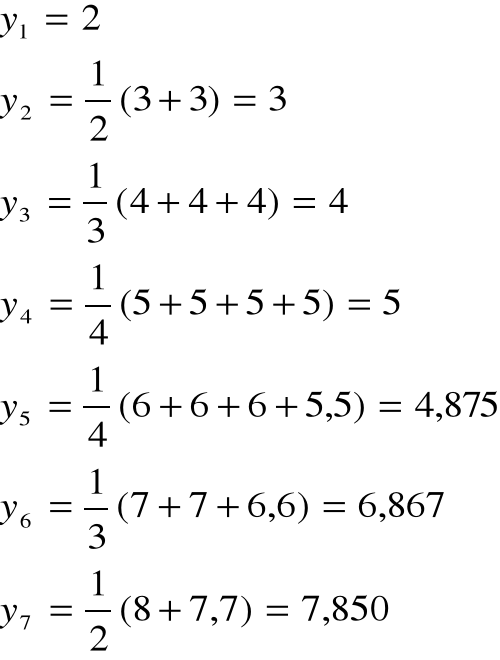
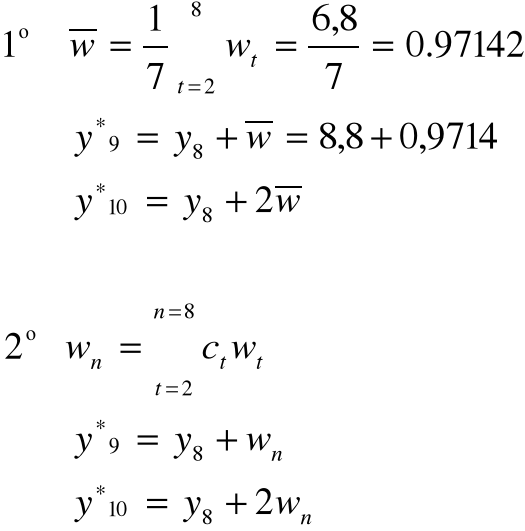
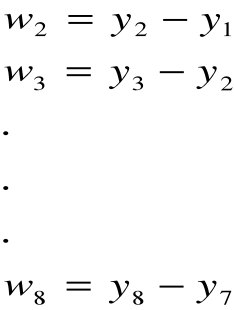
ti |
y(1) |
t´i |
tiyi |
(ti´)2 |
y*(1) |
1 |
2 |
-2 |
-4 |
4 |
2 |
2 |
3 |
-1 |
-3 |
1 |
3 |
3 |
5 |
0 |
0 |
0 |
4 |
4 |
3 |
1 |
3 |
1 |
5 |
5 |
7 |
2 |
14 |
4 |
6 |
∑ |
20 |
0 |
10 |
10 |
|
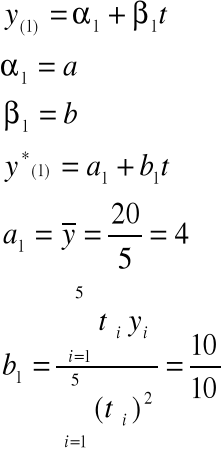
![]()
ti |
y(1) |
t´i |
tiyi |
(ti´)2 |
Yi*(4) |
4 |
3 |
-2 |
-6 |
4 |
4,4 |
5 |
7 |
-1 |
-7 |
1 |
5,5 |
6 |
7 |
0 |
0 |
0 |
6,6 |
7 |
8 |
1 |
8 |
1 |
7,7 |
8 |
8 |
2 |
16 |
4 |
8,8 |
∑ |
33 |
0 |
11 |
10 |
33 |
a = 6,6
b = 1,1
wn = 0,968
yT´ =9,768
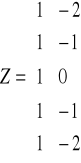
y/ ź= (y(1), y(2), ... , y(n-(k+1))
y/* = (y*(1), y*(2), ..., y*(n-(k+1))
y/* = Z(ZTZ)-1ZTY/
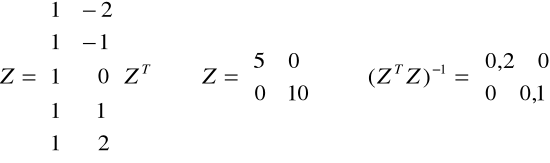
wygładzanie szeregu czasowego za pomocą trendu pełzającego
![]()
Wzory na prognozy na podstawie modeli jednorównaniowych
![]()
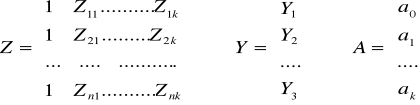
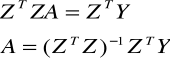
τ>n mτ =(1, mτ1, ... , mτk)
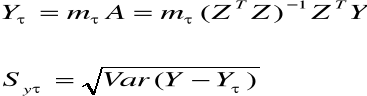
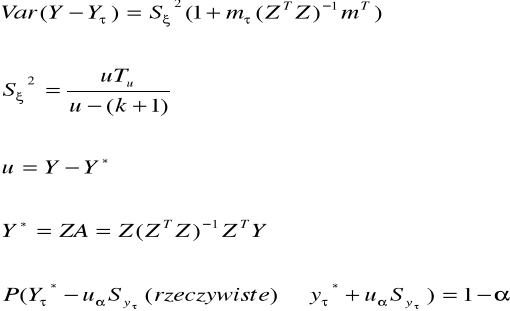
t |
Z0 |
Kt |
Pt |
Zt |
1 |
1 |
60 |
22 |
340 |
2 |
1 |
62 |
24 |
350 |
3 |
1 |
65 |
25 |
370 |
4 |
1 |
66 |
28 |
370 |
5 |
1 |
68 |
29 |
490 |
6 |
1 |
69 |
33 |
410 |
7 |
1 |
72 |
32 |
410 |
8 |
1 |
75 |
35 |
440 |
9 |
1 |
76,18 |
36,8571 |
|
10 |
1 |
78,19 |
38,7148 |
|
ai |
|
58,07 |
20,1429 |
|
bi |
|
2,012 |
1,85714 |
|
m9 |
1 |
76,18 |
36,857 |
|
m10 |
1 |
78,19 |
38,714 |
|
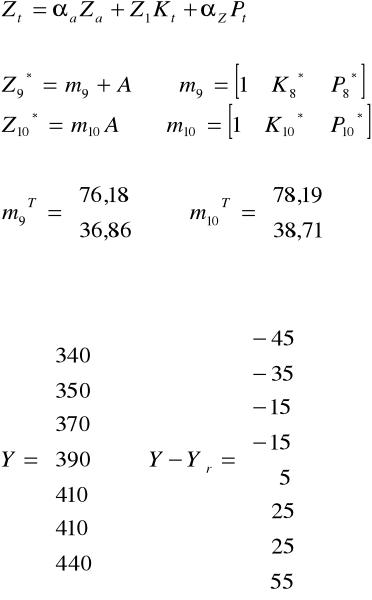
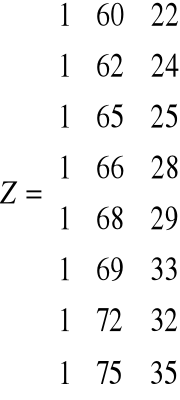
MODELE autoregresyjne
W prognozowaniu zjawisk gospodarczych daje się zauważyć wiele opóźnień w przebiegu niektórych zjawisk w czasie. Obroty handlowe przedsiębiorstw (państw) kształtuje się na podstawie poprzednich kontaktów, wzajemnych powiązań, a przede wszystkim od obrotów z lat poprzednich. Popyt charakteryzuje się cyklami opóźnień związanych z użytkowaniem dóbr.
![]()
FUNKCJA LINIOWA
![]()
FUNKCJA LOGARYTMICZNO - LINIOWA
yt- wartość zmiennej prognozowanej
Przykład
Dany jest szereg czasowy składający się z 9 obserwacji: y1, ... , y9 tzn : 102, 109, 121, 132, 124, 139, 154, 174, 207.
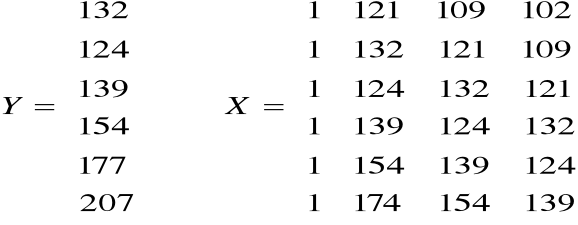
Wyznaczamy modele autoregresji:
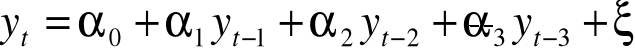
Parametry modelu
doczytać
Metody opisowe prognozowania
prognozowanie analogowe,
metody heurystyczne,
prognozowanie scenariuszowe.
1
Rodzaje przewidywań
Nieracjonalne
Racjonalne
Naukowe
Zdroworozsądkowe
y*t = yt-1 +
![]()
(yt-i - yi)
![]()
prosta: y*t =
![]()
ważona: y*t =
gdzie
![]()
![]()
![]()
, t= n+1,..,T
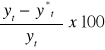
ၷt =
q =
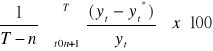
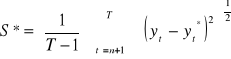
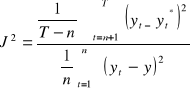
![]()
![]()
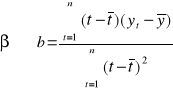
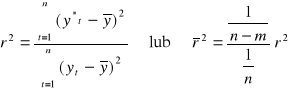
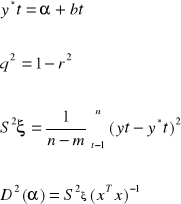
![]()
![]()
![]()
![]()
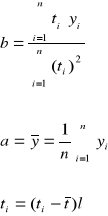
![]()
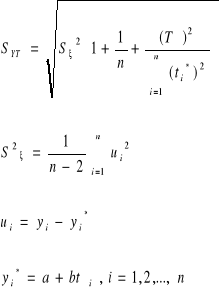
![]()
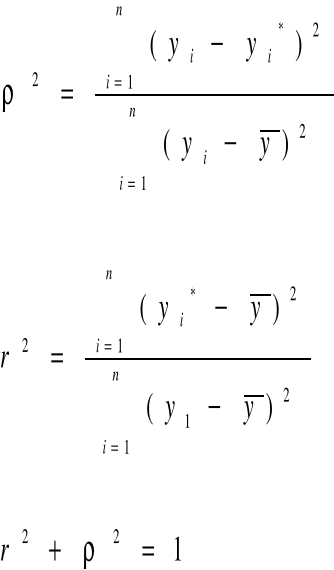
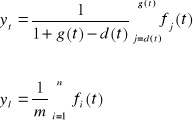
![]()
![]()
![]()
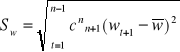
![]()
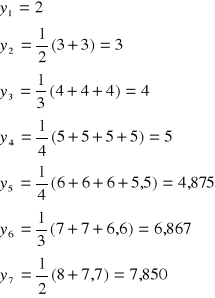
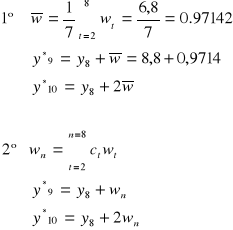
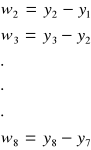
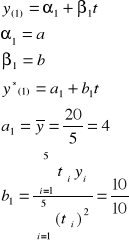
![]()
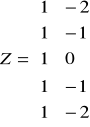
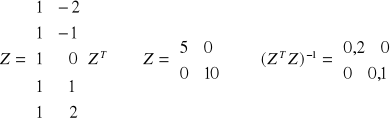
![]()
![]()
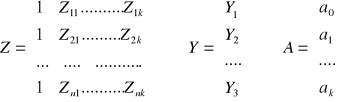
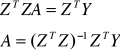
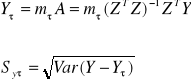
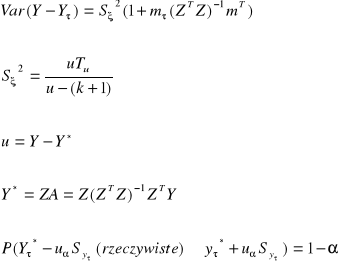
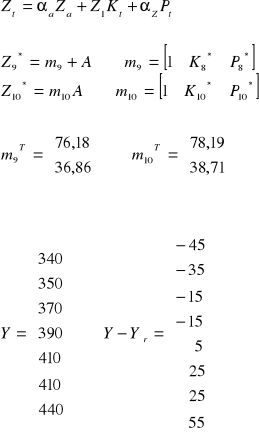
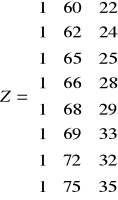
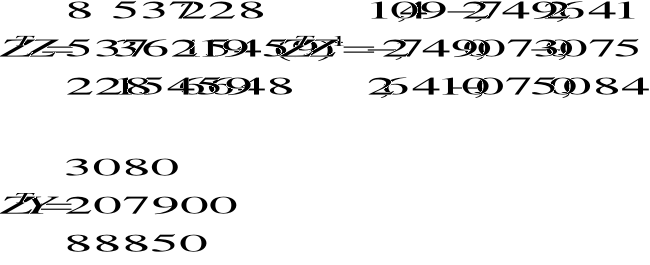
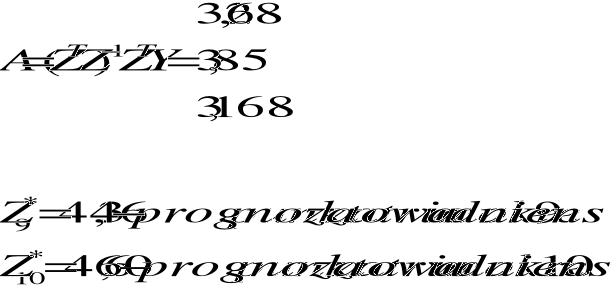
![]()
![]()
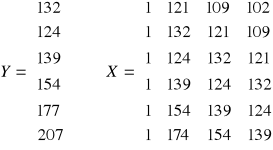
![]()
Wyszukiwarka
Podobne podstrony:
prognozowanie 2, statystyka
prognozy, Płyta farmacja Bydgoszcz, statystyka, pozostałe
Statystyka SUM w4
statystyka 3
Weryfikacja hipotez statystycznych
Zaj III Karta statystyczna NOT st
Metodologia SPSS Zastosowanie komputerów Brzezicka Rotkiewicz Podstawy statystyki
metody statystyczne w chemii 8
Metodologia SPSS Zastosowanie komputerów Golański Statystyki
PROGNOZY GOSPODARCZE DLA POLSKI
prognozowanie 1
Statystyka #9 Regresja i korelacja
06 Testowanie hipotez statystycznychid 6412 ppt
BHP STATYSTYKA
więcej podobnych podstron