Politechnika Śląska w Gliwicach

Wydział Mechaniczno-Technologiczny

Mechanika i Budowa Maszyn

Sprawozdanie

Temat: Wyznaczanie szerokości przerwy energetycznej termistora

Semestr I

Grupa dz: 5

Sekcja 11

1. Mateusz Skuza

2. Robert Respondek

3. Maciej Różański

Termistor - rezystor półprzewodnikowy o ujemnym współczynniku temperaturowym rezystancji i ujemnej rezystancji przyrostowej w części charakterystyki napięciowo-prądowej położonej poza punktem szczytowym; stosowany do stabilizacji napięcia, pomiaru temp., kompensacji zmian temp., detektory promieniowania podczerwonego.

Półprzewodniki - niemetaliczne przewodniki elektronowe (ciała stałe), których rezystywność (opór) jest znacznie większa niż rezystywność przewodników, a znacznie mniejsza niż rezystywność nieprzewodników (izolatorów). W zależności od składu chemicznego rozróżnia się p. proste (jednopierwiastkowe np. krzem, german) oraz złożone

(z dwóch lun więcej pierwiastków np. arsenek galowy , a także mieszany). Stosowane są do budowy przyrządów półprzewodnikowych jak, termistory, diody półprzewodnikowe, lasery półprzewodnikowe, tranzystory itd.

Przewodność właściwa półprzewodników określona jest przez koncentrację nośników „n” i ich ruchliwość „μ”;

σ = e ( n₊μ₊ + n _- μ _- )

W celu zbadania temperaturowej zależności przewodnictwa elektrycznego półprzewodników należy przeanalizować zależność temperaturową koncentracji

i ruchliwości obydwu rodzajów nośników: elektronów i dziur .

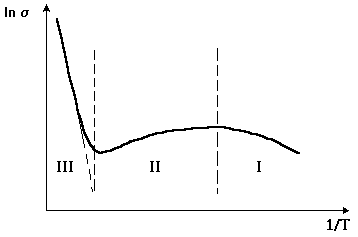
Na poniższym rys. pokazano typowy przebieg temperaturowej zależności przewodności elektrycznej półprzewodnika w skali logarytmiczno - odwrotnościowej

Na wykresie tym można wyróżnić trzy charakterystyczne obszary:

1. w zakresie niskich temperatur praktycznie nie zachodzi termiczna generacja par elektron-dziura, a zjonizowana jest tylko część domieszek; koncentracja zjonizowanych domieszek zależy wykładniczo od temperatury,

2. w zakresie średnich temperatur (-150ºC do +75ºC- dla germanu i -100ºC do +150ºC - dla krzemu) praktycznie wszystkie domieszki są zjonizowane i przewodność praktycznie jest stała, ponieważ w dalszym ciągu nie zachodzi termiczna generacja par elektron-dziura,

3. w zakresie wysokich temperatur dominuje termiczna generacja par elektron-dziura i przewodność elektryczna półprzewodnika zmienia się z temperaturą tak jak dla półprzewodnika samoistnego.

Zewnętrzne pole elektryczne zmienia energie nośników ładunku powodując w konsekwencji zmianę ruchliwości, przy czym ruchliwość może rosnąć lub zmniejszać się zależnie od mechanizmu rozpraszania. Silne pole elektryczne prowadzi do zmiany koncentracji nośników ładunku (jonizacja zderzeniowa, zjawisko Zenera, wewnętrzna emisja polowa, zjawisko Starka).

Termistory są przyrządami półprzewodnikowymi wykorzystującymi zmiany oporności przy zmianie temperatury. Zasadniczo termistory posiadają ujemny współczynnik temperaturowy oporności, a ich opór zmienia się z temperaturą zgodnie ze wzorem:

gdzie R_∞ - oporność w temperaturze dążącej do nieskończoności, B = W_g/2k - stała materiałowa. Tak zwana znormalizowana rezystancja termistora R₂₅ definiowana jest jako jego oporność w temperaturze 25ºC.

Temperaturowy współczynnik oporności określa względną zmianę oporności przy zmianie temperatury o 1 deg.

Temperaturowy współczynnik oporności określa się zwykle w odniesieniu do temperatury 25ºC:

Stan energetyczny elektronów w sieci krystalicznej półprzewodnika opisany jest zgodnie z elektrodynamiką kwantową . Prawdopodobieństwo obsadzania stanu energetycznego o wartości W określa funkcja rozkładu Fermiego-Diraca:

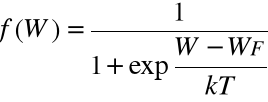
gdzie k - stała Boltzmana, T- temp., W_F - tzw. energia Ferniego, która odpowiada poziomowi, którego prawdopodobieństwo obsadzenia przez elektron wynosi ½ . Położenie poziomu Ferniego jest jednoznacznie związane z koncentracją nośników ładunku w danej temp. Znając rozkład koncentracji stanów w pobliżu dla pasma przewodnictwa W_C :

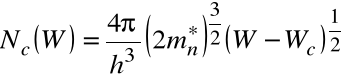
i odpowiednio w pobliżu wierzchołka pasma podstawowego W_V :

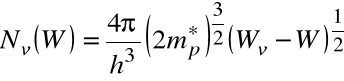
można obliczyć koncentrację nośników w danej temp. W podwyższonych wzorach oznaczono przez m.* - masy efektywne elektronów i dziur, a h - stałą Plancka.

Można wykazać, że iloczyn koncentracji nośników zależy tylko od szerokości przerwy energetycznej W_g i temperatury T:

1. W przypadku rozpraszania na drganiach cieplnych sieci (fononach):

μ_T=μ_OTT^-3/2

gdzie μ_OT jest wielkością stałą. Ze wzrostem temp. liczba fononów rośnie proporcjonalnie do temp., a średnia prędkość nośników jest proporcjonalna do pierwiastka z temp., a więc prawdopodobieństwo zderzenia elektronu (lub dziury) z fononami rośnie proporcjonalnie do T^3/2 .

2. Temperaturowa zależność ruchliwości wynikająca z rozpraszania na jonach domieszek jest bardziej skomplikowana. Dla dostatecznie wysokie temp. wysokiej można otrzymać zależność:

μ₁ = μ₀₁ T^3/2

3. Uwzględniając mechanizm rozpraszania na centrach neutronowych otrzymamy zależność :

μ_D ≈

Uwzględniając zależność koncentracji i ruchliwości nośników ładunku od temperatury, można przewodnictwo elektryczne półprzewodników samoistnych opisać wzorem:

σ= AT ^{3/2 + p}exp

gdzie p. < 1 - stała materiałowa . Jeśli W_g >>kT, to składnik T^{3/2 + p.} zmienia się z temperaturą znacznie wolniej niż wielkość eksponencjalna . Można więc przyjąć, że

AT^3/2+p. = σ₀ = const

i ostatecznie

σ = σ₀e ^{- ( Wg / 2kT)}

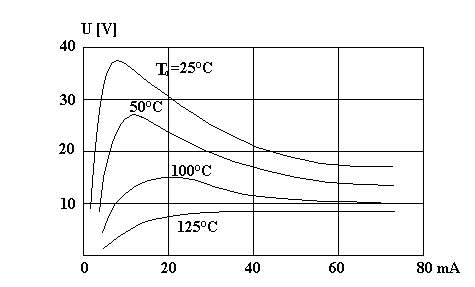
Termistor jest elementem nieliniowym, a wykres spadku napięcia na jego końcach jako funkcji natężenia płynącego prądu jest krzywą z wyraźnym maksimum (zależność tą przedstawiono na poniższym rysunku).

W zakresie niewielkich prądów opór pozostaje stały i obserwuje się prawie liniową zależnością pomiędzy napięciem i natężeniem prądu. Przy wzroście prądu termistor zaczyna się nagrzewać, co powoduje zmniejszanie się rezystancji . Dalszy wzrost prądu powoduje tak silny spadek rezystancji, że napięcie maleje. Zwykle termistory wykonuje się w postaci spieku mieszaniny sproszkowanych materiałów półprzewodnikowych . Termistory z dodatnim współczynnikiem temperaturowym oporności wykonuje się z tytanianu baru i jego roztworów stałych . Można stosować również monokrystaliczny krzem domieszkowany borem. Dobierając odpowiedni skład związków tytaniowych.

Przebieg ćwiczenia:

1. Łączymy obwód wg schematu pokazanego na rysunku :

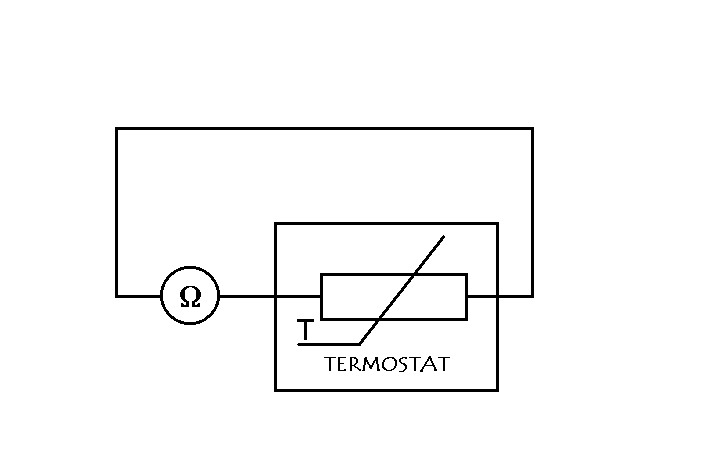
rys. Schemat obwodu do wyznaczania szerokości przerwy energetycznej półprzewodnika

1. Zmieniając temp. kąpieli olejowej w przedziale 20⁰C ÷60 ⁰C co 3 deg mierzymy oporność termistora .

2. Pomiary powtarzamy podczas ochładzania termistora .

3. Rysujemy wykres zależności temperaturowej R = f(T)

4. Rysujemy wykres zależności ln(R)=fi obliczamy współczynniki regresji liniowej tej zależności .

Wyniki przeprowadzonych pomiarów przedstawiono w tabeli nr 1. oraz w tabeli nr 2.

Tab. 1

Lp.	Temperatura T [^0C]	Oporność R [kΩ]
				Grzanie
				1	2	3	4
1	21	27,05	12,4	12,12	53,72
2	26	21,60	10	9,60	41,80
3	31	15,05	6,95	6,53	26,75
4	36	12,60	5,85	5,65	24,17
5	41	11,60	4,97	4,81	20,70
6	46	9,90	4,12	4,07	17,65
7	51	7,89	3,65	3,53	15,75
8	53	7,26	3,34	3,22	14,15
9	56	6,76	3,13	3,02	13,30
10	59	6,16	2,83	2,7	12,96

Tab. 2

L.p	Temperatura	Oporność R [kΩ]
				Chłodzenie
				1	2	3	4
1	56	7,47	3,45	3,40	15,45
2	53	8,38	3,90	3,82	17,66
3	50	9,49	3,42	4,35	19,44
4	47	10,66	4,97	4,88	21,84
5	44	11,69	5,43	5,32	24
6	41	12,94	5,97	5,88	27,33
7	38
8	35
9	32

Obliczamy szerokość przerwy energetycznej półprzewodnika wg. wzoru W_g=2kB i przeprowadzamy rachunek błędów.

Opracowanie wyników.

Obliczamy błędy pomiarowe rezystancji ze wzoru:

0,15%w + 3c

gdzie, w - wskazanie miernika

c - waga ostatniej cyfry

Termistor I

Tab. 3

Lp.	Wskazanie miernika	Błąd	Błąd po zaokrągleniu
1	27,05	0,071	0,07
2	21,60	0,062	0,06
3	15,05	0,052	0,05
4	12,60	0,048	0,05
5	11,60	0,047	0,05
6	9,90	0,044	0,04
7	7,89	0,041	0,04
8	7,26	0,04	0,04
9	6,76	0,04	0,04
10	6,16	0,039	0,04

Termistor II

Tab. 4

Lp.	Wskazanie miernika	Błąd	Błąd po zaokrągleniu
1	12,4	0,048	0,05
2	10	0,045	0,04
3	6,95	0,04	0,04
4	5,85	0,038	0,04
5	4,97	0,037	0,04
6	4,12	0,036	0,04
7	3,65	0,035	0,03
8	3,34	0,035	0,03
9	3,13	0,034	0,03
10	2,83	0,034	0,03

Termistor III

Tab. 5

Lp.	Wskazanie miernika	Błąd	Błąd po zaokrągleniu
1	12,12	0,048	0,05
2	9,60	0,043	0,04
3	6,53	0,037	0,04
4	5,65	0,035	0,04
5	4,81	0,037	0,04
6	4,07	0,036	0,04
7	3,53	0,035	0,03
8	3,22	0,035	0,03
9	3,02	0,035	0,03
10	2,7	0,034	0,03

Termistor IV

Tab. 6

Lp.	Wskazanie miernika	Błąd	Błąd po zaokrągleniu
1	53,72	0,087	0,09
2	41,80	0,067	0,07
3	26,75	0,066	0,06
4	24,17	0,057	0,06
5	20,70	0,052	0,05
6	17,65	0,048	0,05
7	15,75	0,046	0,05
8	14,15	0,044	0,04
9	13,30	0,041	0,04
10	12,96	0,038	0,04

Zmieniamy temperaturę z Celcjuszy na Kelwiny. Obliczamy zmienne x_i =1/T oraz y_i = lnR dla każdego pomiaru.

Tab. 7

Lp.	Temperatura w K	1/K (x)	Ln(R) [y1]	Ln(R) [y2]	Ln(R) [y3]	Ln(R) [y4]
1	294	0,00340	3,297	2,518	2,495	3,984
2	299	0,00334	3,073	2,303	2,261	3,433
3	304	0,00328	2,711	1,939	1,876	3,268
4	309	0,00324	2,534	1,766	1,732	3,185
5	314	0,00318	2,451	1,603	1,571	3,031
6	319	0,00313	2,293	1,416	1,404	2,871
7	324	0,00308	2,066	1,295	1,261	2,757
8	326	0,00307	1,982	1,206	1,169	2,649
9	329	0,00304	1,911	1,141	1,105	2,588
10	332	0,00301	1,818	1,04	0,993	2,482
Wartość średnia:	315	0,003177	2,24998	1,6227	1,5867	3,0248

Z powyższych danych rysujemy wykres zależności R = f(T) oraz ln(R) = 1/k. Obliczamy regresję liniową z zastosowaniem wartości średnich.

Dla termistora I

Tab. 8

Lp.	x	y1	x*y1	x^2	Y1^2
1	0,00340	3,297	0,011209	0,00001156	10,870
2	0.00334	3,073	0,010264	0,00001115	9,443
3	0,00328	2,711	0,008892	0,00001076	7,350
4	0,00323	2,534	0,008185	0,00001043	6,421
5	0,00318	2,451	0,007794	0,00001011	6,007
6	0,00313	2,293	0,007177	0,00000980	5,258
7	0,00308	2,066	0,006363	0,00000949	4,268
8	0,00307	1,982	0,006085	0,00000942	3,928
9	0,00304	1,911	0,005809	0,00000924	3,652
10	0,00301	1,818	0,005472	0,0000906	3,305
Wartość średnia:	0,003176	2,4136	0,0178131	0,000019332	6,0502

Dla termistora II

Tab. 9

Lp.	x	y2	x*y2	x^2	y2^2
1	0,00340	2,518	0,008561	0,00001156	6,34
2	0,00334	2,303	0,007692	0,00001115	5,304
3	0,00328	1,939	0,006360	0,00001076	3,760
4	0,00324	1,766	0,005704	0,00001043	3,119
5	0,00318	1,603	0,005098	0,00001011	2,570
6	0,00313	1,416	0,004432	0,00000980	2,005
7	0,00308	1,295	0,003989	0,00000949	1,677
8	0,00307	1,206	0,003702	0,00000942	1,454
9	0,00304	1,141	0,003469	0,00000924	1,302
10	0,00301	1,04	0,003130	0,0000906	1,082
Wartość średnia:	0,003177	1,6227	0,005214	0,000019299	2,8613

Dla termistora III

Tab. 10

Lp.	x	y3	x*y3	x^2	y3^2
1	0,00340	2,495	0,008483	0,00001156	6,225
2	0,00334	2,261	0,007552	0,00001115	5,112
3	0,00328	1,876	0,006153	0,00001076	3,519
4	0,00324	1,732	0,005612	0,00001043	2,999
5	0,00318	1,571	0,004996	0,00001011	2,468
6	0,00313	1,404	0,004394	0,00000980	1,971
7	0,00308	1,261	0,003921	0,00000949	1,590
8	0,00307	1,169	0,003589	0,00000942	1,366
9	0,00304	1,105	0,003359	0,00000924	1,221
10	0,00301	0,993	0,002989	0,00000906	0,986
Wartość średnia:	0,003177	1,5867	0,005105	0,000010102	2,7457

Dla termistora IV

Tab. 11

Lp.	x	y4	x*y4	x^2	y4^2
1	0,00340	3,984	0,013546	0,00001156	15,872
2	0,00334	3,433	0,012468	0,00001115	13,9352
3	0,00328	3,268	0,010719	0,00001076	10,6798
4	0,00324	3,185	0,010319	0,00001043	10,1442
5	0,00318	3,031	0,009638	0,00001011	9,1869
6	0,00313	2,871	0,008986	0,00000980	8,2426
7	0,00308	2,757	0,008574	0,00000949	7,601
8	0,00307	2,649	0,008129	0,00000942	7,0172
9	0,00304	2,588	0,007867	0,00000924	6,6977
10	0,00301	2,482	0,007470	0,00000906	6,1603
Wartość średnia:	0,003177	3,0248	0,009722	0,000010102	9,55369

Z błędów rezystancji wyznaczamy dane potrzebne do obliczenia błędów pomiarowych:

Termistor I

Tab. 12

Lp.	x	y1	x*y1	x^2	y1^2
1	0,00340	-2,64508	-0,009	0,00001156	6,996448
2	0,00334	-2,78062	-0,0093	0,00001115	7,731848
3	0,00328	-2,95651	-0,0097	0,00001076	8,740951
4	0,00324	-3,03655	-0,0098	0,00001043	9,220636
5	0,00318	-3,05761	-0,0097	0,00001011	9,348979
6	0,00313	-3,12357	-0,0098	0,00000980	9,75669
7	0,00308	-3,19418	-0,0098	0,00000949	10,20279
8	0,00307	-3,21888	-0,0099	0,00000942	10,36119
9	0,00304	-3,21888	-0,0098	0,00000924	10,36119
10	0,00301	-3,24419	-0,0098	0,00000906	10,52477
Wartość średnia:	0,003177	-3,04761	-0,00966	0,000010102	9,324549

Termistor II

Tab. 13

Lp.	x	y2	x*y2	x^2	y2^2
1	0,00340	-3,03655	-0,0103	0,00001156	9,220636
2	0,00334	-3,10109	-0,0104	0,00001115	9,616759
3	0,00328	-3,21888	-0,0106	0,00001076	10,36119
4	0,00324	-3,27017	-0,0106	0,00001043	10,69401
5	0,00318	-3,29684	-0,0105	0,00001011	10,86915
6	0,00313	-3,32424	-0,0104	0,00000980	11,05057
7	0,00308	-3,35241	-0,0103	0,00000949	11,23865
8	0,00307	-3,35241	-0,0103	0,00000942	11,23865
9	0,00304	-3,38139	-0,0103	0,00000924	11,4338
10	0,00301	-3,38139	-0,0102	0,00000906	11,4338
Wartość średnia:	0,003177	-3,27154	-0,01039	0,000010102	10,71572

Termistor III

Tab. 14

Lp.	x	y3	x*y3	x^2	y3^2
1	0,00340	-3,03655	-0,0103	0,00001156	9,220636
2	0,00334	-3,14656	-0,0105	0,00001115	9,90084
3	0,00328	-3,29684	-0,0108	0,00001076	10,86915
4	0,00324	-3,35241	-0,0109	0,00001043	11,23865
5	0,00318	-3,29684	-0,0105	0,00001011	10,86915
6	0,00313	-3,32424	-0,0104	0,00000980	11,05057
7	0,00308	-3,35241	-0,0103	0,00000949	11,23865
8	0,00307	-3,35241	-0,0103	0,00000942	11,23865
9	0,00304	-3,35241	-0,0102	0,00000924	11,23865
10	0,00301	-3,38139	-0,0102	0,00000906	11,4338
Wartość średnia:	0,003177	-3,28921	-0,01044	0,000010102	10,82987

Termistor IV:

Tab. 15

Lp.	x	y4	x*y4	x^2	y4^2
1	0,00340	-2,44185	-0,0083	0,00001156	5,962631
2	0,00334	-2,70306	-0,009	0,00001115	7,306533
3	0,00328	-2,7181	-0,0089	0,00001076	7,388068
4	0,00324	-2,8647	-0,0093	0,00001043	8,206506
5	0,00318	-2,95651	-0,0094	0,00001011	8,740951
6	0,00313	-3,03655	-0,0095	0,00000980	9,220636
7	0,00308	-3,07911	-0,0095	0,00000949	9,480918
8	0,00307	-3,12357	-0,0096	0,00000942	9,75669
9	0,00304	-3,19418	-0,0097	0,00000924	10,20279
10	0,00301	-3,27017	-0,0098	0,00000906	10,69401
Wartość średnia:	0,003177	-2,93878	-0,0093	0,000010102	8,695973

Obliczamy współczynniki regresji oraz odchylenia standardowe tych współczynników stosując wzory:

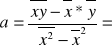
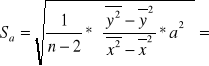
Dla pierwszego termistora:

a = 3821

b = - 9,844

S_a = 5636500

S_b = 17900

Dla drugiego termistora:

a = 3868

b = -10,760

S_a = 5786500

S_b = 18360

Dla trzeciego termistora:

a = 3913

b = -10,887

S_a = 5786400

S_b = 18627

Dla czwartego termistora:

a = 3819

b = -9,158

S_a = 5635300

S_b = 17910

Błędy dla pierwszego termistora:

a = 1370

b = - 7,422

S_a = 749914

S_b = 2391

Dla drugiego termistora:

a = 802,618

b = -5,833

S_a = 262411

S_b = 833,548

Dla trzeciego termistora:

a = 789,044

b = -5,81

S_a = 254411

S_b = 808,128

Dla czwartego termistora:

a = 1966

b = -9,042

S_a = 1545012

S_b = 4911

Obliczamy szerokość przerwy energetycznej poszczególnych termistorów z wzoru W_g=2kB zmieniając jednostki z dżuli na elektronowolty:

1eV = 1.60210*10^-19 J

Termistor I:

W_g = 10,56722*10^-20 J

W_g = 0,65933 eV

Termistor II:

W_g = 10,70797*10^-20 J

W_g = 0,66809 eV

Termistor III:

W_g = 10,77151*10^-20 J

W_g = 0,680 eV

Termistor IV:

W_g = 10,5400*10^-20 J

W_g = 0,65756 eV

Obliczamy błędy pomiarowe:

Termistor I:

W_g = 3,77740*10^-20 J

W_g = 0,244 eV

Termistor II:

W_g = 2,21619*10^-20 J

W_g = 0,142 eV

Termistor III:

W_g = 2,173874*10^-20 J

W_g = 0,137 eV

Termistor IV:

W_g = 5,51136*10^-20 J

W_g = 0,345 eV

Ostateczny wynik:

Termistor I:

W_g =0,65933 ± 0,236 eV

Termistor II:

W_g = 0,66806 ± 0,138 eV

Termistor III:

W_g = 0,673 ± 0,136 eV

Termistor IV:

W_g = 0,65752 ± 0,344 eV

Wnioski z przeprowadzonego ćwiczenia:

Na dokładność otrzymanych wartości wpłynęła dokładność przyrządów pomiarowych, jakie wyznaczają temperaturę i opór.

Pomiary oporu termistora w zależności od temperatury, wykonujemy za pomocą cyfrowego miernika oporu z dokładnością 0,15% +3C wskazania miernika. Minimalny błąd odczytu oporu oraz szybki czas reakcji miernika wpływają na wynik w bardzo małym stopniu.

15

---