Politechnika Częstochowska

Wydział Elektryczny

Laboratorium elektrotechniki

Temat: Siatkowe modelowanie pola

1999-04-15

Wykonujący:

Marek Kijowski

Rafał Klimas

Robert Jagielski

1. Cel ćwiczenia..

Ćwiczenie polega na zamodelowaniu fizycznego pola elektrostatycznego

za pomocą modelu siatkowego dyskretnego , składającego się z siatki w

węzłach której znajdują się rezystory (model elektrycznego pola przepływowego).

2. Idea metody siatkowej.

Metoda siatkowa modelowania pól elektrostatycznych polega na zastąpieniu

fizycznego pola modelem siatkowym , który składa się z siatki rezystorów

(model dyskretny) o danej rezystancji , połączonych między sobą w węzłach

siatki o określonych odstępach.

Model pola fizycznego można opisać równaniami różnicowymi , a znając warunki

brzegowe, czyli wartość potencjału w określonych węzłach można wyznaczyć

wartość potencjału w pozostałych węzłach.

Metoda różnic skończonych rozwiązywania zagadnień brzegowych należy do

grupy metod przybliżonych . Występujące tu błędy wynikają przede wszystkim

z przejścia od równań różnicowych. Ponadto występują błędy związane z

przeliczaniem wartości rzeczywistych na wartości modelowe.

Błędy te można zmniejszyć przez odpowiedni dobór siatki (kwadratowa,

prostokątna, biegunowa), przez zagęszczenie siatki , lub zmianę wartości

wszystkich lub niektórych rezystorów budujących siatkę.

Dokładność obliczeń można także zwiększyć przez wprowadzenie różnic

wyższych rzędów, ale to prowadzi do rozbudowania równań i komplikuje metodę.

W przypadku gdy nie jest wymagana wysoka dokładność, do wyznaczenia

wartości pola stosuje się różne modele analogowe lecz przede wszystkim

modele siatkowe.

Zasady modelowania są tutaj stosunkowo proste, wprowadzenie warunków

brzegowych oraz pomiary potencjału w węzłach charakteryzują się wysoką

dokładnością.

Wadą tych urządzeń jest niestabilność rezystancji przejścia elementów

nastawnych wykorzystywanych w bardziej rozbudowanych układach .

(V₁-V₀ )/R₁ + (V₃-V₀)/R₃ + (V₂-V₀)/R₂ + (V₄-V₀)/R₄ = 0

_i = k_ * V_i

Układając n - równań (n - liczba węzłów pomiarowych) oraz uwzględniając warunki brzegowe (dane wartości potencjału w określonych węzłach) można obliczyć wartości potencjału we wszystkich węzłach .

Do obliczeń numerycznych najlepiej użyć maszyn matematycznych (mikrokomputer).

3. Przebieg pomiarów.

Węzły podziału obszaru badanego pola w metodzie różnic skończonych

odpowiadają węzłom (gniazdom pomiarowym) odpowiedniej tablicy pomiarowej

siatkowego modelu elektrycznego.

Między węzły tablicy pomiarowej są włączone rezystory, a w układach przystosowanych do rozwiązywania bardziej skomplikowanych zagadnień

również kondensatory i cewki.

Szukane rozwiązanie zagadnienia brzegowego polega na zamodelowaniu

równania opisującego pole oraz dokonaniu pomiaru wartości potencjału

w węzłach, a następnie przeliczeniu tych wartości na szukaną wielkość

pola zgodnie z zależnością :

_i = k_ * V_i

Modelowanie równania sprowadza się do przeniesienia geometrii obszaru pola na tablicę pomiarową siatkowego modelu elektrycznego

(w odpowiedniej skali przyjmując odpowiednie x, y ), a następnie wprowadzeniu warunków brzegowych .

Warunki brzegowe pierwszego rodzaju, tzn. dane jako wartości pola,

realizuje się przez przyłożenie do odpowiednich węzłów brzegu napięć

odpowiadających wartościom potencjału _i w tych punktach brzegowych .

4. Modele pomiarowe .

W trakcie trwania ćwiczenia używaliśmy siatkowego modelu pola

o wymiarach 25 na 25 punktów pomiarowych, czyli o 625 punktach.

Model był zbudowany z rezystorów połączonych w następujący sposób:

5. Tabele pomiarowe i wykresy.

a).Układ płaszczyzna-ostrze.

25,57	23,37	22,01	20,24	18,51	16,78	15,13	13,49	11,92	10,41	9	7,65	6,4	5,25	4,22	3,28	2,47	1,79	1,17	0,7	0,35	0,11
25,57	23,76	21,99	20,21	18,47	16,74	15,07	13,44	11,86	10,34	8,9	7,59	6,3	5,15	4,1	3,17	2,35	1,65	1,06	0,59	0,23
25,55	23,74	21,94	20,16	18,39	16,67	14,97	13,33	11,73	10,19	8,74	7,37	6,1	4,94	3,88	2,94	2,12	1,41	0,82	0,35
25,54	23,72	21,88	20,09	18,3	16,54	14,82	13,16	11,54	9,97	8,49	7,08	5,78	4,6	3,83	2,6	1,77	1,06	0,47
25,53	23,66	21,61	20	18,17	16,39	14,63	12,93	11,27	9,66	8,14	6,71	5,4	4,18	3,1	2,14	1,3	0,58
25,48	23,61	21,76	19,88	18,03	16,21	14,4	12,64	10,93	9,26	7,7	6,23	4,87	3,64	2,53	1,56	0,71
25,48	23,58	21,68	19,76	17,87	16,01	14,13	12,31	10,52	8,8	7,17	5,63	4,22	2,96	1,83	0,85
25,46	23,53	21,61	19,65	17,71	15,79	13,85	11,97	10,07	8,25	6,52	4,91	3,44	2,15	1,02
25,42	23,47	21,53	19,53	17,55	15,55	13,55	11,57	9,57	7,6	5,73	4,02	2,5	1,18
25,33	23,42	21,45	19,41	17,99	15,36	13,26	11,14	9	6,87	4,81	4,96	1,36
25,39	23,39	21,38	19,32	17,25	18,17	12,99	10,76	8,44	6,03	3,69	1,66
25,37	23,37	21,34	19,29	17,17	15,03	12,8	10,47	7,94	5,16	2,2
25,37	23,35	21,34	19,28	17,13	14,99	12,72	10,33	7,68	4,49

b). Układ dwa trójkąty.

26,69	25,85	24,96	23,96	22,87	21,67	20,39	19,98	17,54	16,03	14,49	12,95	11,4	9,88	8,45	7,07	5,79	4,59	3,49	2,5	1,61	0,78
26,73	25,93	25,05	24,04	22,97	21,76	20,46	18,07	17,6	16,07	14,5	12,93	11,36	9,84	8,37	6,99	5,69	4,49	3,39	2,41	1,33	0,73
26,2	26,07	25,23	24,25	23,15	21,94	20,62	18,21	17,7	16,12	14,52	12,89	11,29	9,72	8,23	6,81	5,49	4,28	31,8	2,21	1,36	0,63
27,01	26,36	25,54	24,58	23,47	22,24	20,08	18,43	17,87	16,25	14,55	12,85	11,18	9,54	7,99	6,53	5,18	3,95	2,85	1,88	1,07	0,52
	26,79	25,95	25,02	23,89	22,66	21,25	18,74	18,1	16,38	14,8	12,8	11,04	9,3	7,68	6,15	4,75	3,49	2,38	1,42	0,62
		26,62	25,64	24,51	23,23	21,77	20,16	18,43	16,57	14,67	12,74	10,84	8,98	7,25	5,64	4,19	2,89	1,75	0,79
			26,64	25,29	23,96	22,42	20,27	18,87	16,48	14,76	12,65	10,56	8,57	6,69	4,99	3,46	2,12	0,96
				26,24	24,86	23,25	21,45	19,38	17,19	14,86	14,52	10,21	8,02	5,97	4,14	2,53	1,17
					25,98	24,31	22,36	20,13	17,64	15,02	12,36	9,75	7,29	5,06	3,08	1,41
						25,66	23,59	21,09	18,26	15,24	12,16	9,15	6,31	3,81	1,72
							25,19	22,38	19	15,5	11,85	8,37	4,97	2,21
								21,28	19,95	15,75	11,63	7,43	3,11
									20,79	15,94	11,45	6,56

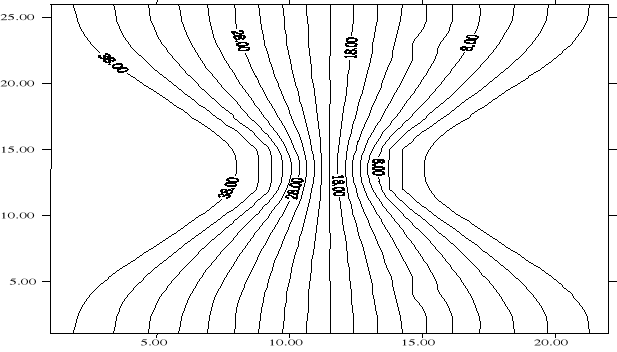
c). Układ żłobek- płaszczyzna.

3,87	3,86	3,88	3,87	3,79	3,72	3,63	3,54	3,41	3,31	3,28	3,27	3,24
7,71	7,76	7,72	7,63	7,57	7,41	7,27	7,06	6,86	6,63	6,45	6,31	6,23
12,22	11,61	11,59	11,54	11,41	11,23	11,08	10,7	10,34	9,93	9,61	9,38	9,25
15,64	15,54	15,52	15,42	15,35	15,15	14,85	18,38	17,31	13,12	12,61	12,24	12,08
19,52	19,51	19,39	19,37	19,33	19,14	18,74	18,12	17,8	16,23	15,49	14,96	14,81
23,51	23,52	23,47	23,44	23,36	23,22	21,94	22,29	20,57	19,85	18,15	17,59	17,29
								23,76	21,75	20,55	19,85	19,46
								25,15	23,45	22,32	21,62	23
								25,92	24,63	23,69	23,08	22,78
								26,4	25,46	24,74	24,25	23,99
								26,74	26,02	25,52	25,11	24,96
								26,99	26,53	26,15	25,89	25,75
								27,19	26,9	26,66	26,49	26,4
								27,36	27,19	27,11	27,03	26,99

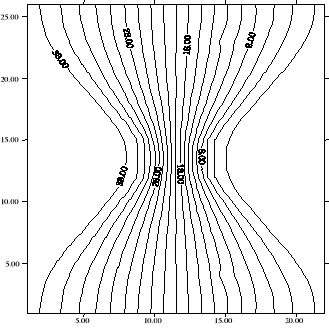
6.Wnioski:

W trakcie trwania ćwiczenia badaliśmy rozkład pola pomiędzy dwoma

różnoimienne naładowanymi płytami. Wykreślone linie ekwipotencjalne

odpowiadają oczekiwaniom. Błędy i niedokładności spowodowane są

niedoskonałością modelu, wpływem zmian napięcia zasilającego

i zmianami parametrów obwodu i miernika cyfrowego używanego

w trakcie trwania ćwiczenia.

Układ był symetryczny, co widać na wykresie. Można było poprzestać

na pomiarach z jednej części modelu (np. dolnej) i odbić je symetrycznie.

Jednak w trakcie trwania ćwiczenia wykonaliśmy wszystkie pomiary

i dlatego wykres nie jest w pełni symetryczny.

---