Numer ćwiczenia	Data	Imię i Nazwisko Dawid Tyszer		Wydział Elektryczny		Semestr III		Grupa 6 Nr lab.
Prowadzący dr A. Krzykowski			Przygotowanie		Wykonanie		Ocena

Temat: Wyznaczanie pętli histerezy ferromagnetyku za pomocą halotronu.

Podstawy teoretyczne. Metodyka pomiarowa.

Szczególny efekt dotyczący kilku pierwiastków (Fe, Co, Ni, Gd, Dy), ich związków oraz stopów, także z innymi pierwiastkami, przyczynia się do uzyskania dużego stopnia ich namagnesowania. Dzieje się to za sprawą oddziaływania, tzw. oddziaływania wymiennego, które występuje w tych metalach oraz związkach, nazywanych ferromagnetykami. Powoduje on sprzęganie z sobą momentów magnetycznych atomów w sposób sztywno-równoległy. To uporządkowanie nie odnosi się do całego materiału, lecz do pewnych obszarów - domen. W ich obrębie dipole magnetyczne zawsze ustawione są równolegle względem siebie, natomiast przy braku namagnesowania poszczególne domeny wykazują różne kierunki uporządkowania wobec pozostałych domen. Magnesowanie prowadzi zatem do porządkowania całych domen, których kierunek dąży do uzyskania kierunku zewnętrznego pola magnetycznego. Łatwo sobie wyobrazić, że po osiągnięciu pożądanego ustawienia przez wszystkie domeny, nie jest możliwy dalszy proces magnesowania materiału, bowiem ten osiąga wówczas stan nasycenia. Oczywiście zakładamy, że opisywanemu przebiegowi zjawiska towarzyszy wciąż zewnętrzne pole magnetyczne. Po jego odjęciu i uwzględnieniu efektu, o którym była mowa wcześniej, ferromagnetyk pozostaje namagnesowany, choć wartość indukcji jest mniejsza od tej w stanie nasycenia. Tę wartość nazywamy pozostałością magnetyczną. Aby zupełnie pozbyć się namagnesowania, należy zadziałać polem magnetycznym o odpowiedniej wartości, zwanej polem koercji oraz o kierunku przeciwnym do tego, który początkowo magnesował. Jeżeli pole będzie wzrastało, przekraczając wartość pola koercji, dojdzie do ponownego porządkowania domen, lecz w przeciwnym kierunku (zgodnie z nowym kierunkiem pola). Znów jest możliwe osiągnięcie stanu nasycenia. Proces jest analogiczny, przeciwne pole magnetyczne niweluje namagnesowanie. Kolejne przekroczenie wartości pola koercji magnesuje materiał zgodnie z pierwotnym kierunkiem pola. Stan nasycenia zamyka pętlę.

Dalszym rozważaniom oraz samemu doświadczeniu towarzyszyć będzie ferromagnetyk w kształcie pierścienia, na który nawinięta jest cewka toroidalna. Prąd w cewce bez rdzenia wytwarza pole magnetyczne o indukcji B₀:

.

W powyższym wzorze n jest liczbą zwojów, która przypada na jednostkę długości cewki, i_m natężeniem prądu płynącego w cewce, µ₀ przenikalnością magnetyczną próżni, która wynosi 4π·10^-7 H/m.

Po umieszczeniu w cewce rdzenia, można zaobserwować znaczny wzrost indukcji pola. Wiemy już, że zewnętrzne pole magnetyczne powoduje powstanie własnego ferromagnetyku. Skoro cewka, przez którą przepływa prąd, wytwarza pole magnetyczne indukujące pole w rdzeniu, wartość indukcji wynikowego pola magnetycznego jest sumą indukcji B₀ (pola wytwarzanego przez cewkę) i B_M (pola rdzenia):

,

co można wyrazić także w następujący sposób:

,

gdzie µ jako przenikalność magnetyczna ośrodka jest bezwymiarową wielkością określającą stosunek indukcji wynikowego pola magnetycznego do pola wytwarzanego przez cewkę.

Dlatego, że µ silnie zależy od natężenia H pola magnetycznego, wytwarzanego przez samą cewkę, to zaś jest proporcjonalne do natężenia prądu magnesującego i_m, bowiem:

,

zależność indukcji B od prądu magnesującego nie jest liniowa.

Pełny przebieg zależności indukcji całkowitego pola magnetycznego od natężenia zewnętrznego pola magnetycznego określany jest pętlą histerezy.

Do przedstawienia pętli histerezy potrzebna jest znajomość indukcji magnetycznej występującej w cewce z rdzeniem oraz natężenia pola magnesującego. Znana ilość zwojów przypadająca na jednostkę w solenoidzie oraz wiedza na temat przepływającego przezeń prądu magnesującego wystarczy do wyznaczenia natężenia pola. Jeśli chodzi o indukcję, do jej wyznaczenia służy halotron, który bazuje na zjawisku Halla. Polega ono na tym, że na cienkiej płytce przewodnika lub półprzewodnika, przez którą przepływa prąd i na którą, prostopadle do kierunku prądu, działa pole magnetyczne, powstaje różnica potencjałów między jej brzegowymi punktami, wywołana siłą Lorentza. Efekt ten ilustruje poniższy rysunek.

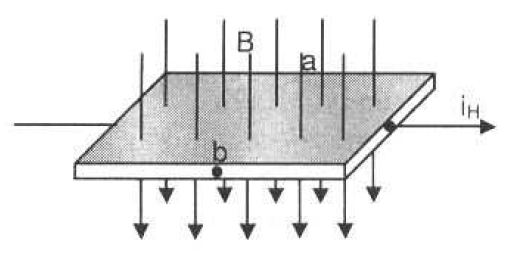
Przez płytkę płynie prąd i_H. Pole magnetyczne o indukcji B, działające prostopadle do płytki, powoduje powstanie siły Lorentza, która spycha ładunki elektryczne od punktu a do b, w wyniku czego tworzy się różnica potencjałów, zwana też napięciem Halla.

Poniżej znajduje się schemat układu dokonującego pomiaru napięcia Halla.

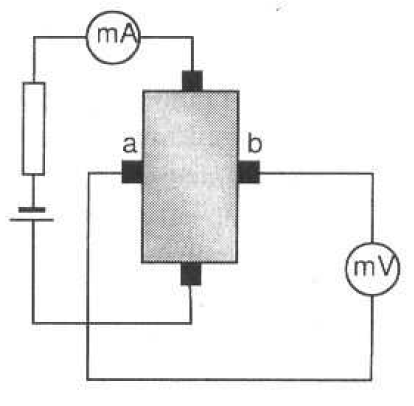
Znany prąd, napięcie Halla oraz tzw. czułość halotronu umożliwia wyznaczenie indukcji pola magnetycznego działającego na płytkę.

Napięcie Halla V_H jest proporcjonalne do płynącego przez halotron prądu i_H, indukcji magnetycznej B oraz czułości halotronu γ, który to współczynnik określony jest przez indywidualne właściwości przyrządu (np. rodzaj materiału, wielkość halotronu):

.

Po przekształceniu otrzymujemy wzór na wartość indukcji:

.

Halotron umieszczany jest w wąskiej szczelinie materiału ferromagnetycznego, wyciętej prostopadle do linii pola magnetycznego wytwarzanego przez rdzeń. Wartość indukcji w takiej szczelinie nie różni się wiele od wartości we wnętrzu ferromagnetyku.

Ostatecznie dwie wielkości podlegają pomiarom: napięcie Halla V_H oraz prąd magnesujący i_m. Układ pomiarowy składa się z dwóch części. Pierwszą stanowi układ zasilania uzwojenia magnesującego, który zawiera źródło prądu stałego, amperomierz i przełącznik kierunku prądu. Część druga to obwód pomiaru napięcia Halla, który zawiera halotron, zasilacz halotronu i miliwoltomierz. Schemat układu przedstawia poniższy obrazek.

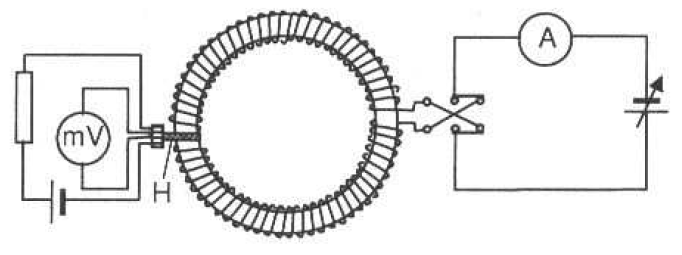
Część pierwsza znajduje się na prawo od toroidu, część druga po lewej stronie.

Pomiary i obliczenia.

Do wyznaczeniu pętli histerezy ferromagnetyku według przedstawionych uprzednio wzorów potrzebna jest znajomość pięciu wielkości, przy czym trzy z nich to wielkości stałe, znane, nie zmieniające się podczas pomiarów. Oto one:

• i_H = (12,0 ± 0,5) mA (natężenie prądu płynącego przez halotron)

• γ = (150 ± 5) V/AT (czułość halotronu)

• n = 6 / cm (liczba zwojów przypadająca na 1 cm)

Dwie pozostałe, V_H (napięcie Halla) oraz i_m (prąd magnesujący) są wielkościami zmiennymi, zależnymi od siebie, wpływającymi na kształt pętli histerezy, zatem podlegają one pomiarom.

Poniższa tabela przedstawia wyniki pomiarów V_H oraz i_m. Prąd magnesujący regulowany był w zakresie od 0 do 3 A, również dla przeciwnego kierunku jego przepływu. Wykonany został także pomiar dla krzywej magnesowania pierwotnego. Miałby on sens, gdyby pierścień był uprzednio rozładowany. W przeciwnym wypadku nie ma możliwości na pozyskanie właściwej krzywej magnesowania pierwotnego. Mimo to, w tabeli pomiarowej ten pomiar został uwzględniony.

Lp.	im [A]	VH [V]		Lp.	im [A]	VH [V]		Lp.	im [A]	VH [V]
1	0,00	0,111		17	1,19	0,178		33	-2,01	-0,202
2	0,42	0,121		18	0,87	0,163		34	-1,64	-0,195
3	0,75	0,131		19	0,44	0,142		35	-1,24	-0,182
4	1,06	0,141		20	0,18	0,125		36	-0,84	-0,170
5	1,34	0,152		21	0,00	0,111		37	-0,38	-0,141
6	1,69	0,169		22	-0,18	0,090		38	0,00	-0,111
7	1,98	0,178		23	-0,41	0,061		39	0,46	-0,033
8	2,29	0,188		24	-0,87	-0,007		40	0,74	-0,012
9	2,68	0,201		25	-1,21	-0,055		41	1,08	0,034
10	2,91	0,208		26	-1,72	-0,121		42	1,51	0,093
11	3,00	0,211		27	-2,17	-0,168		43	1,95	0,143
12	2,71	0,208		28	-2,55	-0,195		44	2,37	0,179
13	2,47	0,205		29	-2,79	-0,207		45	2,77	0,197
14	2,14	0,199		30	-3,00	-0,216		46	3,00	0,206
15	1,81	0,192		31	-2,73	-0,213
16	1,55	0,188		32	-2,41	-0,208

Kolejnym etapem doświadczenia jest obliczenie wartości indukcji magnetycznej oraz natężenia pola dla każdego z pomiarów napięcia Halla i natężenia prądu magnesującego. Wyjątkiem jest pierwsze dziesięć, gdzie zakres natężenia prądu magnesującego zmienia się od 0 do 3 A, bowiem wartości te z pewnością nie odzwierciedlają prawidłowej krzywej magnesowania pierwotnego. Powodem tego jest brak rozmagnesowania pierścienia przed dokonaniem pomiarów. Skądinąd według polecenia nie należało tego czynić. Tak więc do przedstawienia pełnej pętli histerezy ferromagnetyku wystarczą nam pomiary z zakresu natężenia i_m od 3 do -3A (przy 0 zmiana kierunku prądu, stąd „-”) oraz od -3 do 3 A.

Dokonywane obliczenia obejmują jednocześnie błędy pomiarowe wyznaczone dla obu szukanych wielkości, a wszystkie otrzymane wyniki prezentuje jedna tabela.

Do obliczenia błędu wielkości złożonej stosuję różniczkę logarytmiczną.

Znane są błędy danych wielkości i_H, γ, które wynoszą odpowiednio Δi_H = 0,5 mA, Δγ = 5 V/AT. Niepewności pomiarowe wielkości prostych V_H i i_m to kolejno ΔV_H = 0,001 V, Δi_m = 0,01 A.

Przekształcając odpowiednio wzór na indukcję pola magnetycznego działającego na halotron:

,

można w prosty sposób wyznaczyć wzór na niepewność ΔB:

.

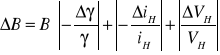
W ten sam sposób postępuję z drugą wielkością - natężeniem pola magnetycznego. Ponieważ

,

wzór na niepewność będzie miał postać:

.

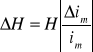
Mając wszystkie potrzebne wzory, dokonuję przykładowego obliczenia dla jednego z pomiarów:

i_m = 2,71 A

V_H = 0,208 V

T

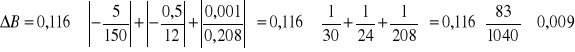
T

A/m

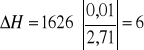
A/m

Poniższa tabela zestawia pomiary wraz z wynikami B i H dokonanych na ich podstawie obliczeń oraz niepewności otrzymanych wielkości.

Lp.	im [A]	VH [V]	B [T]	H [A/m]	ΔB [T]	ΔH [A/m]
1	3,00	0,211	0,1172	1800	0,0093	6,0
2	2,71	0,208	0,1156	1626	0,0092	6,0
3	2,47	0,205	0,1139	1482	0,0091	6,0
4	2,14	0,199	0,1106	1284	0,0088	6,0
5	1,81	0,192	0,1067	1086	0,0086	6,0
6	1,55	0,188	0,1044	930	0,0084	6,0
7	1,19	0,178	0,0989	714	0,008	6,0
8	0,87	0,163	0,0906	522	0,0073	6,0
9	0,44	0,142	0,0789	264	0,0065	6,0
10	0,18	0,125	0,0694	108	0,0058	6,0
11	0,00	0,111	0,0617	0	0,0052	6,0
12	-0,18	0,090	0,05	-108	0,0043	6,0
13	-0,41	0,061	0,0339	-246	0,0031	6,0
14	-0,87	-0,007	-0,0039	-522	0,0008	6,0
15	-1,21	-0,055	-0,0306	-726	0,0028	6,0
16	-1,72	-0,121	-0,0672	-1032	0,0056	6,0
17	-2,17	-0,168	-0,0933	-1302	0,0076	6,0
18	-2,55	-0,195	-0,1083	-1530	0,0087	6,0
19	-2,79	-0,207	-0,115	-1674	0,0092	6,0
20	-3,00	-0,216	-0,12	-1800	0,0096	6,0
21	-2,73	-0,213	-0,1183	-1638	0,0094	6,0
22	-2,41	-0,208	-0,1156	-1446	0,0092	6,0
23	-2,01	-0,202	-0,1122	-1206	0,009	6,0
24	-1,64	-0,195	-0,1083	-984	0,0087	6,0
25	-1,24	-0,182	-0,1011	-744	0,0081	6,0
26	-0,84	-0,170	-0,0944	-504	0,0076	6,0
27	-0,38	-0,141	-0,0783	-228	0,0064	6,0
28	0,00	-0,111	-0,0617	0	0,0052	6,0
29	0,46	-0,033	-0,0183	276	0,0019	6,0
30	0,74	-0,012	-0,0067	444	0,0011	6,0
31	1,08	0,034	0,0189	648	0,002	6,0
32	1,51	0,093	0,0517	906	0,0044	6,0
33	1,95	0,143	0,0794	1170	0,0065	6,0
34	2,37	0,179	0,0994	1422	0,008	6,0
35	2,77	0,197	0,1094	1662	0,0088	6,0
36	3,00	0,206	0,1144	1800	0,0091	6,0

Otrzymane wyniki posłużą do wykreślenia pętli histerezy ferromagnetyku, co jest celem tego ćwiczenia. Poniżej znajduje się pożądany wykres. Dla kilku wybranych punktów wykreślone zostały prostokąty błędów.

Wnioski.

Wykres pętli histerezy ferromagnetyku sporządzony na podstawie dokonanych pomiarów jest bardzo zbliżony do teoretycznego. Ewentualne odchylenia oczywiście mogą być spowodowane niepewnościami oraz błędami pomiarowymi. Przy wykonywaniu doświadczenia istotna była ostrożna regulacja prądu magnesującego, bowiem indukcja B pola magnetycznego zależna jest także, jak widać zresztą z wykresu, od „historii” próbki, czyli od aktualnego jej stanu. Wszelkie „cofnięcia” pokrętła ustawiającego prąd mogą mieć wpływ na otrzymanie nieprawidłowych, a raczej niepożądanych wyników.

- 7 -

---