1. Podstawowe pojęcia mechaniki płynów

Przedmiotem mechaniki płynów są zagadnienia ruchu i równowagi płynów, ze szczegól-nym uwzględnieniem ich oddziaływania na sąsiadujące z nimi ciała stałe.

Podstawową cechą charakteryzującą płyny i odróżniającą je od ciał stałych jest nietrwałość kształtu.

Płynem nazywamy postać materii zmieniającą swój kształt w sposób trwały pod działa-niem dowolnie małych sił zewnętrznych, byle tylko ich działanie trwało dostatecznie długo.

Opór, który towarzyszy zmianom kształtu ciała stałego, zależy od wielkości odkształcenia. Ciało stałe poddane działaniu sił zewnętrznych zmienia swój kształt w sposób bądź nietrwały - sprężysty, bądź trwały - plastyczny.

Opór towarzyszący zmianom kształtu obszaru płynu zależy od prędkości odkształce-nia. Ta cecha płynów wynika z ich lepkości, czyli własności charakteryzującej zdolność płynu do przenoszenia naprężeń stycznych. Zmiana kształtu określonego obszaru płynu może następować na przykład w wyniku zanurzenia w nim ciała stałego, czy też zmianę położenia ciała stałego względem rozpatrywanego obszaru. Powolnym ruchom ciał stałych w płynie towarzyszą niewielkie opory ruchu. Rosną one wydatnie wraz ze wzrostem prędkości ciała stałego względem otaczającego go płynu, czyli ze wzrostem prędkości odkształcania płynu.

Płyny dzielimy na ciecze i gazy.

Cieczami nazywamy płyny, które zachowują niemal stałą objętość pod działaniem nawet znacznych sił zewnętrznych czy zmian temperatury.

Gazami nazywamy płyny, które nie posiadają stałej objętości. Określona masa gazu może zajmować dowolną objętość.

W cieczach poszczególne cząsteczki nie zajmują stałych miejsc w sieci krystalicznej,
jak to ma miejsce w ciałach stałych, ale zmieniają swoje położenie, pozostając jednakże pod działaniem sił spójności - przyciągania. Wynika stąd niezmienność objętości przy nietrwałości kształtu. W gazach natomiast, ze względu na znacznie większe odległości między cząsteczka-mi, siły spójności praktycznie nie występują. Cząsteczki gazu, pozostając w ciągłym ruchu, zderzają się ze sobą.

Dzięki temu, że zmiana kształtu obszaru płynu może się odbywać w wyniku działania dowolnie małych sił zewnętrznych, płyny przyjmują kształty ujmujących ich zbiorników. Ciecze zachowują przy tym swoją objętość, czyli zajmują taką część zbiornika, jaka odpowiada ich własnej objętości, tworząc powierzchnię swobodną. Natomiast dowolna masa gazu zamknięta w określonej przestrzeni wypełnia ją całkowicie.

Analizując zjawiska zachodzące w przyrodzie dokonujemy zawsze pewnych uproszczeń, uwzględniając jedynie istotne dla danego zjawiska cechy fizyczne i oddziaływania. Posługujemy się zatem modelami zjawisk. Stopień skomplikowania modelu zależy od potrzeb analizy, a często również od znajomości empirycznej zjawiska, jak też od dostępnych metod matematycznych. Podstawowym uproszczeniem stosowanym w klasycznej mechanice płynów jest pominięcie struktury cząsteczkowej płynu i traktowanie go jako ośrodka ciągłego - continuum. Rozumiemy przez to, że płyn wypełnia przestrzeń w sposób ciągły - bez „pustych miejsc”.

Rysunek zamieszczony poniżej przedstawia wyodrębniony z przestrzeni obszar płynu V. Jest on ograniczony powierzchnią zamkniętą A i może sąsiadować ze ścianami ciał stałych oraz elementami płynu, które nie wchodzą w skład rozpatrywanego obszaru.

W otoczeniu dowolnego punktu obszaru możemy wyodrębnić bardzo małą objętość ΔV zachowującą wszystkie makroskopowe własności fizykalne płynu, która jest nazywana elementem płynu.

Elementem płynu nazywamy taką jego objętość ΔV, której wymiary liniowe są wiel-kościami małymi wyższego rzędu w porównaniu z wymiarami rozpatrywanego obszaru (np. wymiarami liniowymi otaczających go ciał stałych w postaci zbior-ników, przewodów, czy też ciał stałych zanurzonych w płynie). Jednocześnie objętość ΔV zawiera tak dużą liczbę cząstek płynu, że jego własności makroskopowe okreś-lone w stosunku do tej objętości zachowują swój sens.

Traktując płyn jako ośrodek ciągły można zastosować przejście graniczne . Oznacza to, że element płynu może być dowolnie mały. Pozwala to określać własności płynu i wielkości fizyczne opisujące jego stan jako funkcje położenia elementu płynu. Jeżeli każdemu punktowi przestrzeni wypełnionej płynem przyporządkujemy w każdej chwili t wartości liczbowe (jedną lub więcej) określające pewną wielkość fizyczną, wówczas mamy do czynienia z niestacjonarnym (zmiennym w czasie) polem tej wielkości (np. pole temperatury, pole prędkości płynu itp.). Stanowi ono funkcję położenia punktu w przestrzeni i czasu t.

Opis matematyczny zjawisk zachodzących w płynie w trójwymiarowej czasoprzestrzeni wymaga zastosowania przestrzennego układu współrzędnych położenia. Najczęściej jest używany prostokątny układ współrzędnych kartezjańskich (x, y, z) oraz układy współrzęd-nych krzywoliniowych ortogonalnych - o wzajemnie prostopadłych wersorach współrzędnych.
W dalszej części wykładu będziemy się zwykle posługiwać układem współrzędnych (x, y, z), traktowanym jako domyślny.

Miarą ilości materii jest masa. Rozkład masy w obszarze płynu może nie być równomierny. Posługujemy się w związku z tym pojęciem gęstości, która może być różna w poszczególnych punktach rozpatrywanego obszaru.

Gęstością ρ w danym punkcie obszaru płynu nazywamy granicę, do której dąży stosunek masy Δm zawartej w elemencie płynu stanowiącym otoczenie rozpatrywanego punktu do objętości ΔV tego elementu, gdy jego rozmiary dążą do zera:

.

Masę płynu dm zawartą w elementarnej objętości dV można wyznaczyć, wykorzystując przejście graniczne, następująco:

.

Rozkład masy w obszarze płynu określa pole gęstości
, w ogólnym przypadku zmienne w czasie. Masę płynu zawartą w obszarze V wyznacza zatem wyrażenie:

.

1. Siły działające na płyn

Opis zjawisk zachodzących w płynie wymaga określenia działających na niego sił zewnętrznych. Dzielimy je na masowe (lub objętościowe) i powierzchniowe. Siły masowe działają na płyn zawarty wewnątrz rozpatrywanego obszaru. Siły powierzchniowe działają na powierzchni obszaru płynu i przedstawiają oddziaływanie elementów płynu lub ciał stałych sąsiadujących z tym obszarem. W mechanice płynów operuje się pojęciem tzw. sił jednostkowych, odniesionych do jednostki powierzchni bądź jednostki masy płynu (względnie do jednostki objętości - są one wówczas nazywane jednostkowymi siłami objętościowymi, lub objętościową gęstością siły). Pozwala to traktować siły działające na płyn jako pola wielkości fizycznych.

Siły masowe działają na masę płynu zawartą wewnątrz rozpatrywanego obszaru. Są to na przykład siły grawitacji, siły magnetoelektryczne. Oddzielnie powinny być w zasadzie rozpat-rywane tzw. siły bezwładności, które są siłami fikcyjnymi, skierowanymi przeciwnie do sił czynnych i są związane z przyspieszeniami elementów płynu.

Jednostkowa siła masowa
w danym punkcie obszaru płynu jest to granica,
do której dąży stosunek siły masowej
działającej na masę płynu zawartą
w elemencie płynu o objętości ΔV - stanowiącym otoczenie rozpatrywanego punktu - do masy Δm tego elementu, gdy jego rozmiary dążą do zera:

.

Siłę masową, która działa na masę płynu dm zawartą w elementarnej objętości dV przedstawimy, wykorzystując przejście graniczne, następująco:

.

Jednostkowe siły masowe, które działają na płyn zawarty w rozpatrywanym obszarze, tworzą pole wektorowe
. Wypadkową (sumę) sił masowych działających na płyn zawarty w obszarze V opisuje w związku z tym wyrażenie:

,

Związek między jednostkową siłą masową i jednostkową siłą objętościową (objętościową gęstością siły) jest następujący:

.

Siły powierzchniowe działają na powierzchni wydzielonego obszaru płynu ze strony sąsiadujących z tym obszarem elementów płynu bądź ścianek ciał stałych. Na powierzchni swobodnej cieczy działają ponadto siły spowodowane napięciem powierzchniowym, związane z oddziaływaniem międzycząsteczkowym, które na ogół pomijamy.

Jednostkową siłą powierzchniową
(nazywaną również wektorem naprężeń)
w danym punkcie rozpatrywanej powierzchni płynu nazywamy granicę, do której dąży stosunek siły powierzchniowej
wywieranej na element powierzchni ΔA stanowiący otoczenie danego punktu, do pola powierzchni ΔA tego elementu,
gdy jego rozmiary dążą do zera:

.

1 Pa = 1 N/m² .

Wektor kierunkowy powierzchni
jest wektorem jednostkowym o module
.

Uwaga: wektorem kierunkowym drugiej (przeciwnej) strony powierzchni jest
.

W przypadku powierzchni płynu zamkniętej, ograniczającej obszar płynu V, wektor kierunkowy powierzchni
jest kierowany na zewnątrz obszaru. Zgodnie z przedstawionymi wyżej zasadami orientacji powierzchni „patrzymy” od wnętrza obszaru na zewnątrz.

Siłę powierzchniową
działającą na element powierzchni dA przedstawimy, wykorzystując przejście graniczne, następująco:

.

Wypadkową (sumę) sił powierzchniowych działających na rozpatrywaną powierzchnię płynu A opisuje wyrażenie:

,

Moduł, linia działania i zwrot wektora jednostkowej siły powierzchniowej zależą
od ukierunkowania powierzchni w tym punkcie oraz stanu naprężeń w płynie. Jeżeli przez ten sam punkt przestrzeni wypełnionej płynem poprowadzimy inną powierzchnię o innym ukierunkowaniu, wówczas zmieni się również wektor jednostkowej siły powierzchniowej.
W ogólnym przypadku, kiedy płyn jest w ruchu, wektor jednostkowej siły powierzchniowej
w danym punkcie powierzchni płynu nie jest do niej prostopadły. Jego linia działania jest wtedy wynikiem zarówno oddziaływań normalnych jak i oddziaływań stycznych, które występują w płynie lepkim i są związane z prędkością jego odkształcenia postaciowego.

2. Stan naprężeń w płynie

Wektor siły powierzchniowej
, która działa na powierzchnię ΔA płynu, jest zaczepiony
w punkcie O. Ukierunkowanie powierzchni ΔA
w tym punkcie wyznacza wektor kierunkowy
. Obierzmy kierunek normalny n do powierzchni ΔA w punkcie O (oś n) oraz kierunek styczny s
do powierzchni w tym punkcie (oś s) tak wybrany, aby wektor
leżał w płaszczyźnie ns.

Rzuty wektora
na kierunki n i s (miary wektora na osi n i s) przedstawiają dwie skła-dowe tego wektora:
- normalną do powierzchni ΔA i
- styczną do tej powierzchni.

Naprężenia normalne p_nn i styczne p_ns na powierzchni ΔA (w punkcie O) są zdefiniowane następująco:

;
.

Przedstawiają one składowe wektora jednostkowej siły powierzchniowej
. Pierwszy indeks tych składowych wskazuje ukierunkowanie powierzchni w rozpatrywanym punkcie przestrzeni - określone za pomocą wektora jednostkowego
, drugi indeks wskazuje kierunek, do którego naprężenie jest równoległe.

Określenie naprężenia normalnego p_nn i stycznego p_ns w sposób przedstawiony powyżej wymagało odpowiedniego doboru płaskiego układu współrzędnych (n, s), który uwzględniał położenie w przestrzeni linii działania wektora kierunkowego
powierzchni ΔA i linii działania wektora siły powierzchniowej
. Należy zaznaczyć, że zwrot wektora

na powyższym rysunku nie jest dobrany przypadkowo. Wektor ten jest skierowany
do powierzchni płynu ΔA i w przyjętym układzie współrzędnych jego miara na osi n jest ujemna. Wartość naprężenia normalnego p_nn jest w związku z tym również ujemna,
co oznacza, że jest to naprężenie ściskające. Płyny nie przenoszą naprężeń rozciągających, którym jest przypisywana wartość dodatnia - z wyjątkiem szczególnych warunków bardzo szybkich odkształceń, np. występujących przy wybuchach. Naprężenia normalne występujące
w płynach są naprężeniami ściskającymi - przybierają w związku z tym wartości ujemne.

Opis matematyczny sił powierzchniowych w przestrzeni trójwymiarowej musi być jednolity dla wszystkich punktów obszaru płynu, niezależnie od kształtu i położenia rozpatrywanej powierzchni. Konieczne jest zastosowanie w tym celu przestrzennego układu współrzędnych. Można wykazać, że wyznaczenie w takim układzie wektora jednostkowej siły powierzchniowej w danym punkcie powierzchni płynu, o ukierunkowaniu określonym w tym punkcie wektorem kierunkowym
, wymaga wykorzystania 9-ciu wielkości skalarnych
o odpowiednich wartościach, przypisanych temu punktowi obszaru. Wielkości te, zapisane
w formie macierzy kwadratowej, przedstawiają tensor naprężeń S, który w układzie współrzędnych x, y, z ma następującą postać:

.

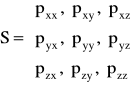
Składowe tensora przedstawiają naprężenia, które występują na trzech wzajemnie prostopadłych elementach powierzchniowych przechodzących przez dany punkt przestrzeni i są odpowiednio prostopadłe do kierunków x, y, z. Pierwszy indeks składowej określa ukierunkowanie elementu powierzchni (kierunek osi współrzędnych prostopadłej do tego elementu). Drugi z indeksów wskazuje kierunek naprężenia - równoległy do odpowiedniej osi współrzędnych. Przykładowo: p_xx - naprężenie (normalne) występujące na elemencie powierzchniowym o ukierunkowaniu zgodnym z osią x (pierwszy indeks) równoległe do osi x (drugi indeks,); p_xy - naprężenie (styczne) na powierzchni o ukierunkowaniu zgodnym z osią x (pierwszy indeks) równoległe do kierunku y (drugi indeks) itd. - patrz rysunek poniżej. Składowe tensora naprężeń p_xx, p_yy, p_zz leżące na jego przekątnej głównej przedstawiają naprężenia normalne, pozostałe 6 składowych to naprężenia styczne.

Uwaga! Ze względu na czytelność rysunku naprężenia na trzech wzajemnie prostopadłych elementach powierzchniowych przechodzących przez dany punkt przestrzeni zostały przedstawione jako występujące na trzech ścianach prostopadłościanu o wymiarach elementarnych, ukierunkowanych zgodnie z kierunkami osi współrzędnych x, y, z. Wszystkim naprężeniom zostały nadane zwroty zgodne ze zwrotem tej osi współrzędnych, do której dane naprężenie jest równoległe. Ich wartości w przyjętym układzie współrzędnych są w związku
z tym dodatnie, co rozszerza poziom uogólnienia również na ciała stałe. Płyny natomiast,
jak wspomniano wyżej, nie przenoszą naprężeń normalnych rozciągających (p_xx, p_yy, p_zz),
czyli o takim zwrocie, jak przedstawiono na rysunku.

Składowe tensora naprężeń mogą mieć różne wartości w poszczególnych punktach obszaru płynu i mogą się zmieniać w tych punktach wraz z upływem czasu: p_xx(x,y,z,t), p_xy(x,y,z,t), p_xz(x,y,z,t), p_yy(x,y,z,t), p_yx(x,y,z,t),…itd. Tensor naprężeń w odniesieniu
do przestrzeni wypełnionej płynem przedstawia zatem w ogólnym przypadku niestacjonarne pole tensorowe, które opisuje stan naprężeń w płynie.

Jednostkową siłą powierzchniową
wyznacza iloczyn wektora kierunkowego powierzchni
i tensora naprężeń S przedstawionych w formie macierzowej:

,

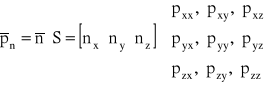
lub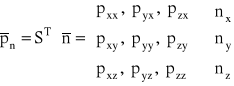
,

gdzie: T - znak transponowania macierzy.

Wykonując operację mnożenia zgodnie z zasadami rachunku macierzowego otrzymamy następujące wyrażenie opisujące wektor jednostkowej siły powierzchniowej:

,

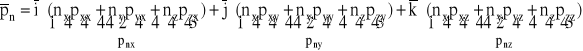
gdzie:
- wersory (wektory jednostkowe) układu współrzędnych x, y, z,

p_nx, p_ny, p_nz - miary (składowe) wektora
na osiach układu współrzędnych x, y, z.

Tensor naprężeń w płynie jest symetryczny. Oznacza to, że składowe leżące po przeciwnych stronach przekątnej głównej są sobie równe: p_xy= p_yx; p_xz=p_zx; p_yz= p_zy. Zachodzi w związku z tym następująca zależność dotycząca wartości naprężeń:

.

3. Ciśnienie

Wartość sumy naprężeń normalnych p_xx, p_yy, p_zz w danym punkcie obszaru płynu nie zależy od orientacji układu współrzędnych w przestrzeni. Przedstawia ona tzw. niezmiennik tensora naprężeń. Wiąże się z nią pojęcie ciśnienia.

Ciśnieniem p w danym punkcie przestrzeni wypełnionej płynem jest nazywana średnia arytmetyczna naprężeń normalnych ściskających dla trzech wzajemnie prostopadłych dowolnie wybranych elementów powierzchniowych przechodzących przez ten punkt:

.

Znak minus w powyższym wzorze wynika z faktu, że płyny przenoszą wyłącznie naprężenia normalne ściskające, które mają wartości ujemne (patrz pkt 1.2). Ciśnienie jest
w związku z tym wielkością skalarną o wartości zawsze dodatniej (równej zeru w absolut-nej próżni, bądź w temperaturze zera bezwzględnego). Rozkład ciśnienia w przestrzeni wypełnionej płynem opisuje pole skalarne
.

W zagadnieniach technicznych często jest stosowane pojęcie ciśnienia względnego (nadciśnienia, podciśnienia), które jest określane w odniesieniu do ciśnienia atmosferycznego p_a:

.

Nadciśnieniem jest nazywane ciśnienie względne p_w>0. Podciśnienie jest to ciśnienie względne p_w<0, którego wartość nie może być jednak mniejsza od (-p_a). Należy zwracać
na to uwagę podczas studiowania tekstów i książek technicznych, ponieważ ich autorzy zapominają czasami zaznaczyć, że posługują się pojęciem ciśnienia względnego, używając skrótowo określenia ciśnienie i stosując symbol p. Również szereg przyrządów stosowanych do pomiaru ciśnienia, zwanych manometrami, w rzeczywistości mierzy ciśnienie względne.

Jednostki ciśnienia:

Jednostką ciśnienia w układzie SI jest pascal: 1 Pa = 1 N/m². Jest to jednostka zbyt mała
dla większości zastosowań technicznych, wykorzystuje się więc jej wielokrotności,
np. megapascal: 1 MPa = 10⁶ Pa.

W zagadnieniach technicznych często jest używana dopuszczona do stosowania jednostka wywodząca się z układu cgs: 1 bar = 10⁶ dyna/cm² = 10⁵ Pa, gdzie 1 dyna = 1 gcm/sek².
Jest ona chętnie stosowana, ponieważ wartość ciśnienia podana w barach jest bardzo zbliżona do wartości podanej w jednostkach układu technicznego, do którego jest przyzwyczajonych wielu inżynierów. Jednostką ciśnienia w tym układzie jest atmosfera techniczna:
, gdzie 1 kG = 9,81 N.

Wartość ciśnienia w płynie może być wyrażona za pomocą wysokości słupa cieczy
o znanej gęstości, przy założeniu stałej, przeciętnej wartości przyspieszenia ziemskiego równej 9,81 m/s². Taką jednostką jest np. 1 Tor, który przedstawia ciśnienie wywierane
przez 1 mm_Hg (rtęci) oraz atmosfera fizyczna: 1 atm, która odpowiada ciśnieniu 760 mm_Hg. Spotykane było również wyrażanie ciśnienia za pomocą wysokości słupa wody w tem-peraturze 4º C, np.:
;
.

Literatura:

1. Prosnak W.: Mechanika płynów, tom I, rozdział 1 i 3, PWN, Warszawa 1970,

2. J. Bukowski, P. Kijkowski: Kurs mechaniki płynów, rozdział 1 pkt 1.1, 1.2, PWN, Warszawa 1980.

3. E. Tuliszka: Mechanika płynów, rozdział 6, PWN, Warszawa 1980,

4. Л. Г. Лoйцянский: Механика жидкости и газа, глава II, § 10, Москва „Наука” 1978.

W. Prosnak: Mechanika płynów tom I, rozdział 3, PWN, Warszawa 1970;

E. Tuliszka: Mechanika płynów, rozdział 6, PWN, Warszawa 1980;

Л. Г. Лoйцянский: Механика жидкости и газа, глава II, § 10, Москва „Наука” 1978.

Dr inż. Janusz Bidziński Mechanika płynów

8

Δm

ΔV

+

-

orientacja powierzchni

druga strona powierzchni

Wektor kierunkowy powierzchni

ΔA

ΔA

O

s

n

Δm

ΔV

p_yz

p_zy

p_zx

p_xz

p_xx

p_zz

p_xy

p_yx

p_yy

z

y

x

∆V

A

V

∆A

y

x

z

---