Projekt z Teorii mechanizmów i maszyn
Akademia Górniczo Hutnicza w Krakowie	Temat: Analiza kinematyczna i kineostatyczna mechanizmu dźwigniowego.	Rok akademicki: 2001/2002	Semestr: 2	Data:
Grupa: 8	Skolimowski Krzysztof	Ocena:	Podpis:

δ    ρ

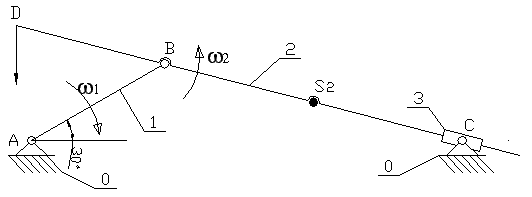
Dane :

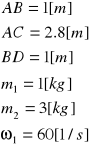
1. Analiza strukturalna mechanizmu.

1. Obliczam ruchliwość i klasę mechanizmu.

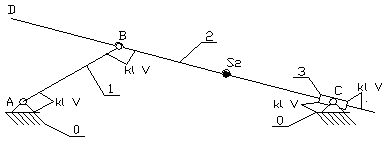
Ruchliwość mechanizmu wynosi :

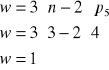
2. Struktura mechanizmu :

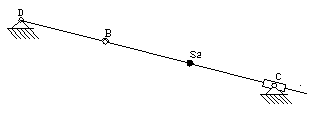
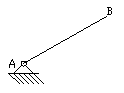
Rys. Człon napędzający Rys. Grupa strukturalna

Człony 2 i 3 tworzą grupę strukturalną klasy II postaci 2

2. Analiza kinematyczna mechanizmu.

2.1 Model mechanizmu w programie AKM.

Zamodelowany mechanizm jest zapisany w postaci pliku AKM „model” na dołączonej dyskietce.

2.2.1 Wyznaczam prędkości liniowe i kątowe oznaczonych na rysunku punktów mechanizmu metodą grafo-analityczną (metoda planów)

Szukam prędkości punktów A, B, C0, C2, C3, D (

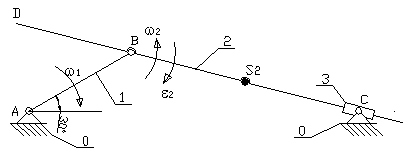
W celu znalezienia prędkości liniowych należy rozwiązać układ równań porównując ich prawe strony.

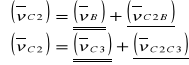
(2.2.0)

Rozwiązaniem układu (2.2.0) jest plan prędkości przedstawiony na rysunku poniżej.

Podziałka prędkości :

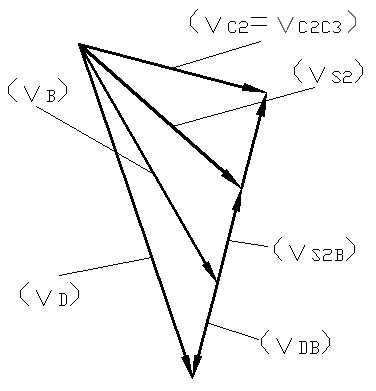
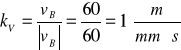
Odpowiednie prędkości wynoszą :

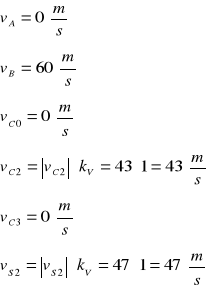
Rys. Plan prędkości mechanizmu jarzmowego.

Prędkość punktu D znajdziemy z zależności :

(2.2.1)

tak więc :

Prędkość kątowa
,
i
wynoszą :

2.2.2 Szukam przyspieszeń punktów B, C2, S2, D (

Przyspieszenie punktu B:

(2.2.2)

gdzie :

ponieważ

Przyjmuje podziałkę przyspieszeń -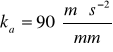

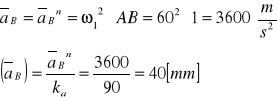
Ponieważ suwak obraca się razem z jarzmem to jego przyspieszenie kątowe jest równe przyspieszeniu kątowemu jarzma, czyli
. W celu znalezienia przyspieszeń liniowych należy rozwiązać układ równań porównując ich prawe strony.

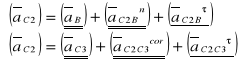
(2.2.3)

gdzie :

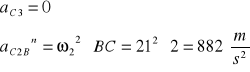
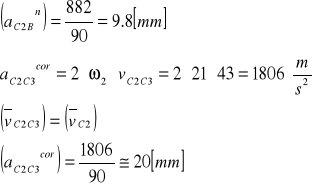
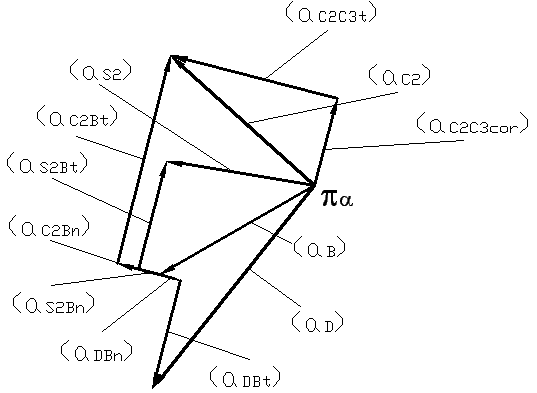
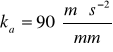
Rys: Plan przyspieszeń mechanizmu jarzmowego

Korzystając z planu przyspieszeń znajdujemy przyspieszenie kątowe „

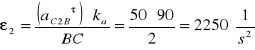
Wyznaczam przyspieszenie punktu D.

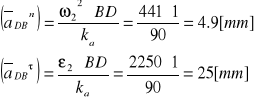
Z planu przyspieszeń wynika, że przyspieszenie punktu D wynosi :

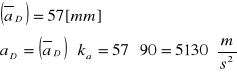
Wyznaczam przyspieszenie punktu S2.

gdzie :

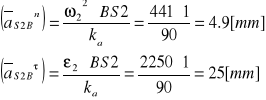
Z planu przyspieszeń wynika, że przyspieszenie punktu S2 wynosi :

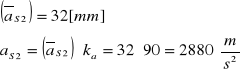
Szukane przyspieszenia wynoszą odpowiednio :

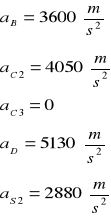
2.2.3 Wyznaczam prędkości i przyspieszenia liniowe oznaczonych na rysunku punktów mechanizmu, oraz prędkości i przyspieszenia kątowe członów metodą analityczną.

Rys. Wielobok wektorowy mechanizmu jarzmowego.

Mechanizm jarzmowy zapisujemy za pomocą wieloboku trzech wektorów. Należy zatem założyć, że
parametry mechanizmu. Jedynym członem o zmiennej długości jest jarzmo 3.

Dane :


=2.8[m]

Szukane :
,
,
,
,
,

Wpisany w mechanizm wielobok wektorów zapisujemy równaniem :

(2.2.4)

Po zrzutowaniu na osie układu otrzymujemy :

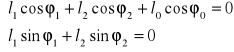
(2.2.5)

Z układu równań wyznaczam długość jarzma

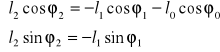
(2.2.6)

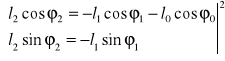
(2.2.7)

Po podniesieniu do kwadratu układu (2.2.6)i dodaniu stronami znajdziemy długość jarzma
:

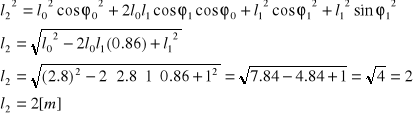
(2.2.8)

Dzieląc układ równań (2.2.6) stronami otrzymujemy :

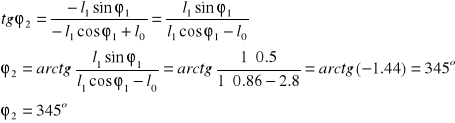
(2.2.9)

Długość jarzma w chwili t wynosi :

Kąt Nachylenia jarzma w chwili t wynosi :

W celu znalezienia prędkości liniowych i kątowych jarzma 2 różniczkujemy pierwsze równanie układu (2.2.5) podstawiając
oraz

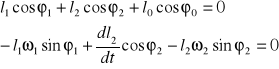
(2.2.10)

Prędkość względna suwaka 3 względem prowadnicy 2 tj.
znajdziemy obracając układ współrzędnych Oxy o kąt
.

(2.2.11)

Ostatecznie prędkość suwaka 3 względem prowadnicy 2:

Prędkość kątową jarzma znajdziemy obracając układ współrzędnych o kąt
.

(2.2.12)

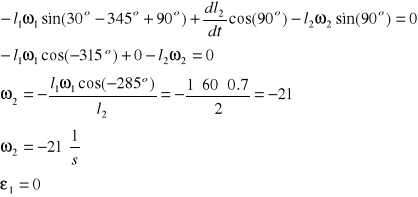
W celu znalezienia przyspieszeń kątowych i liniowych różniczkujemy równanie (2.2.5) podstawiając
oraz
gdzie

Przyspieszenie styczne
suwaka znajdziemy obracając układ współrzędnych o kąt
:

więc :

Obracając układ o kąt
otrzymamy przyspieszenie kątowe jarzma :

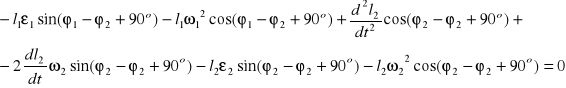
Ostatecznie otrzymujemy :

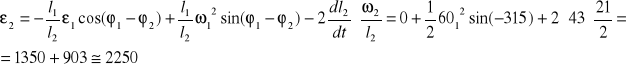
Dla punktu S2 :

Rys. Wielobok wektorowy mechanizmu jarzmowego.

Wpisany w mechanizm wielobok wektorów zapisujemy równaniem :

Po zrzutowaniu na osie układu otrzymujemy :

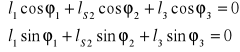
Z układu równań wyznaczam długość jarzma

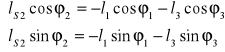
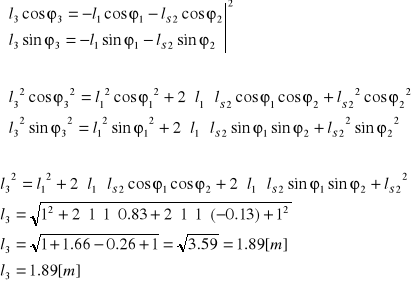
Dzieląc układ równań stronami otrzymujemy :

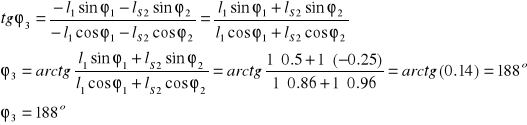
W celu znalezienia prędkości liniowych i kątowych punktu S2 różniczkujemy pierwsze równanie układu podstawiając
oraz
,oraz

Prędkość względna suwaka punktu S2
znajdziemy obracając układ współrzędnych Oxy o kąt
.

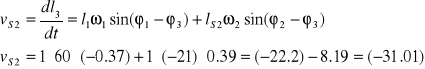
Obliczenia dla punktu D

Rys. Wielobok wektorowy mechanizmu jarzmowego.

Wpisany w mechanizm wielobok wektorów zapisujemy równaniem :

Po zrzutowaniu na osie układu otrzymujemy :

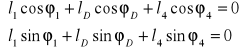
Z układu równań wyznaczam długość jarzma

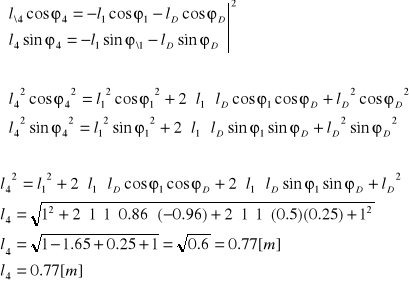
Dzieląc układ równań stronami otrzymujemy :

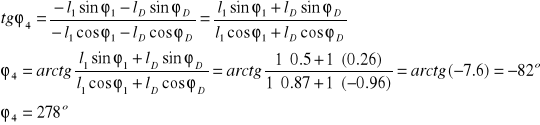
W celu znalezienia prędkości liniowych i kątowych punktu S2 różniczkujemy pierwsze równanie układu podstawiając
oraz
,oraz

Prędkość względna punktu D
znajdziemy obracając układ współrzędnych Oxy o kąt
.

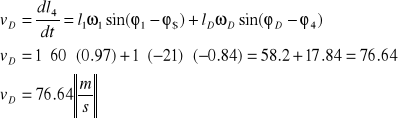
W celu znalezienia przyspieszeń kątowych i liniowych różniczkujemy równanie (2.2.5) podstawiając
oraz
gdzie

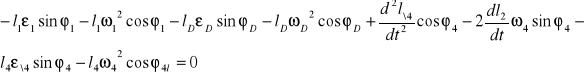
Przyspieszenie
suwaka znajdziemy obracając układ współrzędnych o kąt
:

więc:

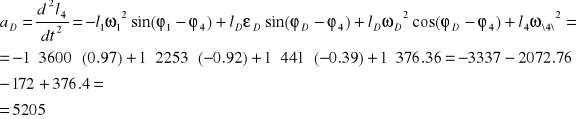
Tabela zestawieniowo-porównawcza wyników obliczeń kilku metod:

	Grafoanalityczna	Analityczna
VC2	42	42
VS2	47	-
VD	77	76.64
ω2	22	21
aC2	3445	3402
aS2	3032
aD	5222	5205
ε2	2253	2253

3. Analiza kinetostatyczna.

3.1 Przyjmuje masy i momenty bezwładności względem środka masy dla wskazanych członów oraz siłę oporu P.

Dane :

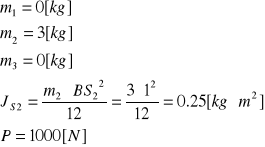
3.2 Obliczam siły bezwładności i momenty od sił bezwładności.

Ponieważ człon 1 traktujemy jako bez masowy i prędkość kątowa
możemy uznać, iż siła bezwładności działająca na ten człon jest równa 0. Podobnie człon 3 traktujemy jako bez masowy

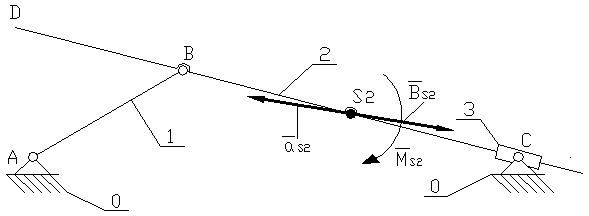
Rys. Przyspieszenie, siłą bezwładności oraz moment od siły bezwładności mechanizmu jarzmowego

Obliczam siłę bezwładności działającą na człon 2.

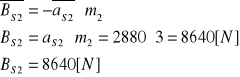
(3.0)

Obliczam moment od siły bezwładności działający na człon 2.

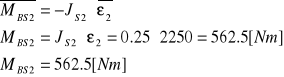
(3.1)

Kierunek działania siły bezwładności jest zgodny z kierunkiem przyspieszenie, zwrot zaś przeciwnie do niego skierowany. Zwrot działania momentu od siły bezwładności jest skierowany przeciwnie do zwrotu przyspieszenia kątowego.

3.3 Wyznaczam reakcje w parach kinematycznych i moment równoważący przyłożony do członu napędzającego mechanizmu metodą grafoanalityczną.

Moment równoważący :

Dane : Szukane : reakcje w parach oraz moment równoważący

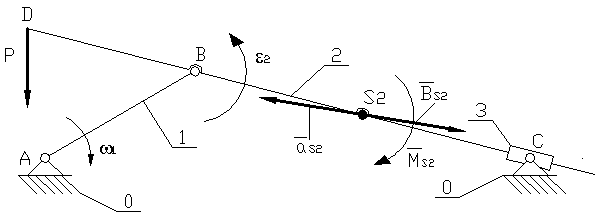
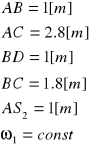
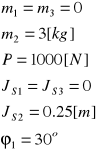
Rys. Mechanizm jarzmowy obciążony siłami zewnętrznymi.

Na rysunku poniżej przedstawiono grupę strukturalną uwolnioną od więzów z przyłożonymi siłami reakcji

Rys. Układ sił zewnętrznych z przyłożonymi siłami zewnętrznymi i reakcjami.

Warunek równowagi sił działających na grupę ma postać:

(3.2)

Korzystając z warunku na równowagę momentów wszystkich sił względem punktu S2 obliczymy wartość reakcji
:

(3.3)

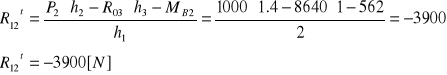
Znak minus mówi o tym, iż zwrot reakcji został przyjęty nieprawidłowo.

Następnie przystępujemy do rozwiązania równania wektorowego metodą grafoanalityczną.

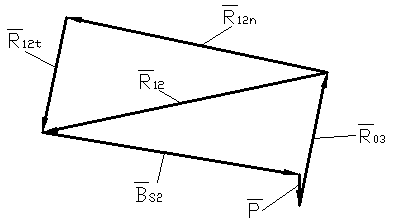
Rys. Plan sił dla grupy strukturalnej (2.3)

Uwzględniając podziałkę z planu sił odczytujemy wartości szukanych reakcji.

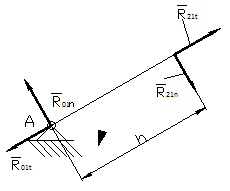
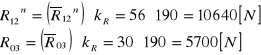
Na rysunku obok przedstawiono człon napędzający

z siłami reakcji. Ponieważ człon traktujemy jako bez masowy siła bezwładności jest równa 0.

W wyniku stałej prędkości kątowej również mo-

ment od siły bezwładności jest równy 0.

Równanie równowagi sił działających na człon napędzający ma postać :

(3.4)

Z równania tego, oraz rysunku wynika iż reakcje w punkcie A są równe co do wartości lecz przeciwnie skierowane aniżeli reakcje w punkcie B.

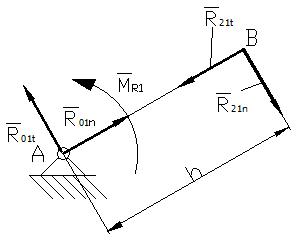
Moment równoważący znajdziemy zapisując równanie sumy momentów działających na

człon napędzający względem punktu A.

Rys. Moment równoważący członu napędzającego

3.4 Sprawdzenie obliczeń momentu równoważącego metodą porównania mocy chwilowych.

Rys. Mechanizm jarzmowy obciążony siłami zewnętrznymi i momentem równoważącym.

Równanie mocy chwilowych dla powyższego przypadku ma postać :

(3.5)

Po rozpisaniu równania (3.5) na iloczyny skalarne :

Ostatecznie poszukiwany moment równoważący wynosi :

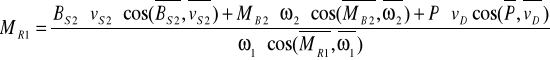
Odpowiednie kąty wynoszą :

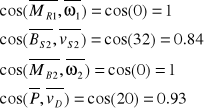
Więc :

Znak minus mówi że zwrot uogólnionego momentu równoważącego jest przeciwny do przemieszczenia i mamy do czynienia z momentem hamującym.

W związku z powyższym możemy uznać, iż obliczenia są poprawne.

---