SZEREGI POTĘGOWE
DEF. 1. Szeregiem potęgowym nazywamy szereg funkcyjny postaci ![]()
, gdzie a0,a1,a2,..., an ,...to współczynniki szeregu zaś x0 to środek szeregu potęgowego.
UWAGA 1. Szereg potęgowy, którego środkiem jest 0 jest postaci ![]()
.
Poniżej podane zostaną własności szeregu potęgowego o środku w 0.
Zbieżność szeregu potęgowego.
UWAGA 2. Każdy szereg potęgowy jest zbieżny w swoim środku.
UWAGA 3. Wyrazy szeregu potęgowego są określone dla wszystkich x rzeczywistych więc każda liczba rzeczywista x jest dla szeregu potęgowego albo punktem zbieżności albo punktem rozbieżności.
TWIERDZENIE 1. Jeśli szereg potęgowy ![]()
jest zbieżny w pewnym punkcie x = c ≠ 0, to jest zbieżny bezwzględnie w otwartym przedziale (-|c|, |c| ) oraz zbieżny jednostajnie w każdym domkniętym podprzedziale tego przedziału.
TWIERDZENIE 2. Jeśli szereg potęgowy ![]()
jest rozbieżny w pewnym punkcie x = w ≠ 0, to jest rozbieżny na zewnątrz przedziału (-|w|, |w| ).
DEF 2.. Obszarem zbieżności szeregu potęgowego ![]()
jest zbiór K=(-r, r), gdzie liczba r jest promieniem zbieżności szeregu.
UWAGA 4.W konkretnych przypadkach obszarem zbieżności szeregu potęgowego 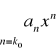
może być
zbiór K=[- r , r) lub K=(- r , r] lub K=[- r , r]. Obszar K będziemy nazywać przedziałem zbieżności.
Podamy teraz dwa twierdzenia dzięki, którym będzie można wyznaczyć promień zbieżności a tym samym obszar zbieżności konkretnego szeregu potęgowego.
TWIERDZENIE 3 Jeżeli mamy dany szereg potęgowy ![]()
i jeżeli 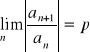
, to:
jeżeli p ≠ 0 wtedy
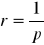
,jeżeli p = 0 wtedy r = ∞,
jeżeli p = ∞ wtedy r = 0.
TWIERDZENIE 4.Jeżeli mamy dany szereg potęgowy 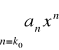
i jeżeli ![]()
, to:
jeżeli p ≠ 0 wtedy
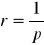
,jeżeli p = 0 wtedy r = ∞,
jeżeli p = ∞ wtedy r = 0.
Przykład 1. Rozważmy szereg potęgowy ![]()
. Zastosujemy twierdzenie 5.
Mamy ![]()
, więc r = 1. Aby ostatecznie ustalić przedział zbieżności tego szeregu należy za x podstawić 1 a następnie -1 . Dla x=1 dostajemy następujący szereg liczbowy ![]()
, który jest szeregiem rozbieżnym, oraz dla x=-1 mamy ![]()
również szereg jest rozbieżny, więc obszar zbieżności K=(-1, 1).
Przykład 2. Rozważmy szereg potęgowy ![]()
. Zastosujemy twierdzenie 5.
Mamy 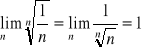
, więc ![]()
. Aby ostatecznie ustalić przedział zbieżności tego szeregu należy za x podstawić 1 a następnie -1 . Dla x=1 dostajemy następujący szereg liczbowy ![]()
, który jest szeregiem rozbieżnym, natomiast dla x=-1 mamy ![]()
szereg anharmonicznym zbieżny, więc obszar zbieżności K=[-1, 1).
Przykład 3. Rozważmy szereg potęgowy ![]()
. Zastosujemy twierdzenie 5.
Mamy 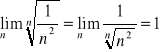
, więc ![]()
. Aby ostatecznie ustalić przedział zbieżności tego szeregu należy za x podstawić 1 a następnie -1 . Dla x=1 dostajemy następujący szereg liczbowy ![]()
, który jest szeregiem zbieżnym, oraz dla x=-1 mamy ![]()
szereg zbieżny, więc obszar zbieżności K=[-1, 1].
Przykład 4. Weźmy szereg potęgowy 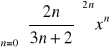
. Ponownie zastosujemy to samo kryterium, 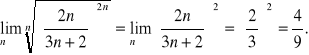
Wobec tego promień zbieżności ![]()
. Przedziałem zbieżności jest zbiór ![]()
. Oczywiście należy jeszcze sprawdzić co dzieje się na końcach tego przedziału, podstawiając w szeregu za x liczby ![]()
i ![]()
.
Przykład 5. Aby ustalić promień zbieżności szeregu ![]()
zastosujemy twierdzenie 4. Mamy 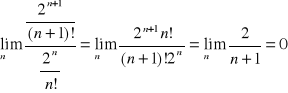
, więc r= ∞ i przedziałem zbieżności tego szeregu jest zbiór (-∞,∞)=R. Oznacza to, że szereg potęgowy jest zbieżny dla każdej liczby rzeczywistej x.
Przykład 6. Promień zbieżności szeregu ![]()
obliczamy ponownie stosując 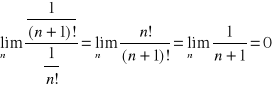
, więc r= ∞ i przedziałem zbieżności tego szeregu jest zbiór (-∞,∞)=R.
Przykład 7. Promień zbieżności szeregu ![]()
obliczamy ponownie stosując ![]()
, więc r=0 i szereg jest zbieżny tylko dla x=0
TWIERDZENIE 5. Jeżeli promieniem zbieżności szeregu potęgowego 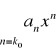
jest liczba r, to obszarem zbieżności szeregu funkcyjnego ![]()
, gdzie y = g(x) - dowolna funkcja jest zbiór K={x∈R: |g(x)| < r}.
Przykład 8
Rozpatrzmy szereg funkcyjny ![]()
. Po podstawieniu t=x2 - 2x +5 dostajemy szereg potęgowy ![]()
ze względu na t. Jak łatwo sprawdzić promieniem zbieżności tego szeregu jest liczba r=5. Jeżeli teraz za t wstawimy liczbę 5, to dostaniemy szereg rozbieżny, jeżeli za t wstawimy liczbę -5, to otrzymamy szereg zbieżny, więc przedziałem zbieżności jest zbiór [-5,5). Aby ustalić obszar zbieżności szeregu ![]()
rozwiązać układ nierówności -5≤ x2 - 2x +5≤5. Rozwiązaniem tego układu jest przedział ![]()
.
W związku z tym obszarem zbieżności szeregu funkcyjnego ![]()
jest zbiór K=(0,2).
TWIERDZENIE 6. Dwa szeregi potęgowe ![]()
i ![]()
można do siebie dodać w następujący sposób: ![]()
.
TWIERDZENIE 7. Szereg potęgowy ![]()
można pomnożyć przez liczbę:![]()
, gdzie λ≠0 i λ∈R.
TWIERDZENIE 8 Jeżeli przedziałem zbieżności szeregu potęgowego ![]()
jest zbiór K=( - r , r ) oraz jego suma jest równa f(x) , to szereg ten w zbiorze K można różniczkować wyraz po wyrazie tzn.:
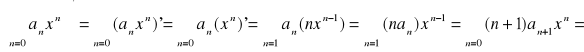
![]()
. Po zróżniczkowaniu otrzymujemy szereg potęgowy, którego promień zbieżności nie ulega zmianie oraz suma jego g(x) jest pochodną sumy szeregu pierwotnego.
Przykład 9. Rozważmy szereg potęgowy ![]()
. Z przykładu 3 wiemy, że obszarem zbieżności jest K=[-1,1]. Rozpatrzmy szereg utworzony z pochodnych wyrazów szeregu pierwotnego
![]()
Zastosujemy twierdzenie 5. Mamy ![]()
, więc r=1. Aby ostatecznie ustalić przedział zbieżności tego szeregu należy za x podstawić 1 a następnie -1 . Dla x=1 dostajemy następujący szereg liczbowy ![]()
, który jest szeregiem rozbieżnym, oraz dla x=-1 mamy ![]()
szereg zbieżny, więc obszar zbieżności K=[-1, 1). Zauważmy, że oba obszary zbieżności różnią się na krańcach przedziałów .
TWIERDZENIE 9 Jeżeli przedziałem zbieżności szeregu potęgowego ![]()
jest zbiór K=( - r , r ), to szereg ten w zbiorze K można całkować wyraz po wyrazie tzn.:
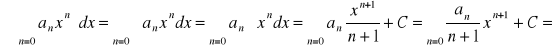
![]()
.
Rozwijanie funkcji w szereg potęgowy
DEF.3. Funkcję y = f (x) nazywamy klasy Cn jeżeli jest n-krotnie różniczkowalna i n-ta pochodna jest funkcją ciągłą.
DEF.4. Funkcję y = f (x) nazywamy gładką jeżeli klasy Cn dla każdego n∈N. Inaczej mówiąc jest funkcją klasy C∞.
TWIERDZENIE 10 (Taylor)
Jeżeli funkcja y = f (x) jest klasy Cn w otoczeniu (a- h , a+ h) punktu a∈R, h > 0, to dla każdego x∈R zachodzi następujący wzór Taylora:
![]()
.Ostatni składnik ![]()
będziemy nazywać resztą, gdzie cx ∈(x, a ) lub cx ∈(a, x )
TWIERDZENIE 11
Jeżeli funkcja y = f(x) jest gładka w otoczeniu (a- h , a+ h) punktu a∈R, h > 0 i ![]()
, to funkcja przedstawia się w postaci szeregu potęgowego Taylora postaci:
![]()
![]()
. Przyjmujemy, że ![]()
Dla a=0 szereg potęgowy Taylora jest szeregiem potęgowym Maclaurina i ![]()
, gdzie ![]()
.
Przykład 10 Rozwiniemy w szereg Maclaurina funkcję ![]()
. Pochodna dowolnego rzędu tej funkcji jest tą samą funkcją, tzn. ![]()
czyli funkcja jest gładka oraz ![]()
, więc wzór jest następujący:
![]()
.
Wyznaczymy promień zbieżności powstałego szeregu potęgowego.
Mamy 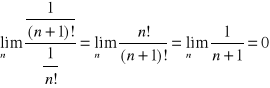
, czyli r= ∞ i przedziałem zbieżności jest cała oś liczbowa, więc funkcja ![]()
rozwija się w szereg potęgowy postaci ![]()
na całej osi liczbowej.
W szczególności jeśli za x podstawimy 1 to otrzymamy wartość liczby e.
![]()
.
a jeśli chcemy obliczyć wartość e z dokładnością do 0.001 sumujemy wyrazy których wartość bezwzględna jest większa od 0.001. Stąd ![]()
ponieważ ![]()
<0.001 .
Aby policzyć wartość ![]()
z dokładnością do 0,01 należy w rozwinięciu ![]()
za x=-2 , stąd
![]()
wystarczy dodać osiem kolejnych razów gdyż ![]()
<0.01.
Przykład 11
Rozwiniemy w szereg potęgowy Maclaurina funkcję y=sinx.
Policzmy pochodne i ich wartości w zerze.
![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
...
Widać, że powtarzają się sekwencje liczb 0,1,0,-1, 0,1,0,-1, ....
W związku z tym mamy
![]()
.
Łatwo sprawdzić, że przedziałem zbieżności tego szeregu jest również cała oś liczbowa, więc dla każdego x rzeczywistego prawdziwy jest wzór ![]()
.
Przykład 12
Podobnie rozwijając w szereg potęgowy Maclaurina funkcję y=cosx otrzymamy prawdziwy na całej osi liczbowej wzór![]()
.
Przykład 13
Rozwiniemy w szereg potęgowy Maclaurina funkcję ![]()
Policzymy kolejne pochodne i ich wartości w zerze.
![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
![]()
, ![]()
...
Mamy
![]()
![]()
Sprawdzimy w jakim zbiorze jest prawdziwy powyższy wzór. W tym celu wyznaczymy promień zbieżności. Policzmy ![]()
, więc przedziałem zbieżności tego szeregu jest zbiór (-1,1). Łatwo można sprawdzić, że dla x=-1 i dla x=1 szereg potęgowy jest rozbieżny. Wobec tego wzór ![]()
jest prawdziwy tylko dla ![]()
.
Przykład 14
Aby rozwinąć w szereg Maclaurina funkcję ![]()
wykorzystamy przykład 13.
W szeregu ![]()
zamiast x wstawimy ![]()
i dostaniemy ![]()
i ostatecznie ![]()
.Obliczamy promień zbieżności powstałego szeregu : ![]()
, więc ![]()
. Korzystając twierdzenia 5 dostajemy, że ![]()
, więc 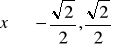
, czyli wzór ![]()
jest prawdziwy dla 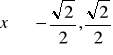
.
Czyli ![]()
dla ![]()
Przykład 15
Aby rozwinąć w szereg Maclaurina funkcję f(x)= ![]()
wykorzystamy rozwinięcie
![]()
dla |x|<1
Zajmijmy się najpierw rozwinięciem 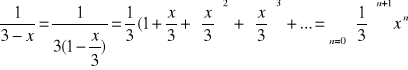
. A teraz f(x)=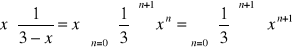
.Obliczamy promień zbieżności powstałego szeregu : 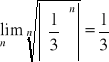
, więc r=3. Czyli szereg 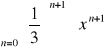
jest zbieżny dla |x|<3
Przykład 16
Posługując się twierdzenia 9 rozwiniemy w szereg Maclaurina funkcję y=arctgx. Proszę zwrócić uwagę, że pochodna tej funkcji ![]()
.
Z poprzedniego przykładu wiemy, że ![]()
.
Całkując obustronnie w obrębie przedziału zbieżności ![]()
dostajemy :
![]()
Podstawiając do obu stron równania ![]()
x=0 dostajemy, że C=0.
Ostatecznie, więc ![]()
w przedziale (-1,1), ponieważ przy całkowaniu promień zbieżności a tym samym przedział zbieżności nie zmienia się.
ZADANIA
1.Obliczyć promień zbieżności szeregu i zbadać zbieżność na krańcach przedziałów zbieżności
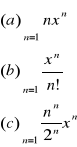
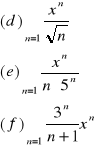
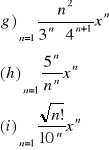
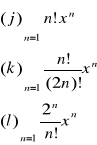
2.Zbadać zbieżność szeregów ![]()
![]()
oraz zbieżność szeregów utworzonych z pochodnych wyrazów tego szeregu.
3.Rozwinąć w szereg potęgowy Maclaurina funkcję
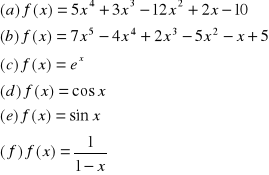
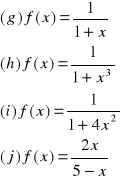
4.Rozwinąć w szereg potęgowy Taylora funkcję
(a) f(x)=1/x w punkcie a=3 (b)f(x)=cos2x w punkcie a=ၰ/3
5.Obliczyć:
sin
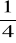
z dokładnością do 0,0001,cos
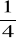
z dokładnością do 0,00001
z dokładnością do 0,001
posługując się rozwinięciem odpowiedniej funkcji w szereg potęgowy .
Wyszukiwarka
Podobne podstrony:
Szeregi funkcyjne i potęgowe, Matematyka, analiza
25 Szeregi potęgowe i ich zbieżność Własności sumy szeregu potęgowego
16 Rozdział 15 Szeregi potęgowe
AMI 24 Szeregi potęgowe
AM23 w04 Szeregi potęgowe
AM2 2 Szeregi potęgowe
8 szeregi potęgowe
szeregi potęgowe
23 ciagi i szeregi funkcyjne 6 2 szeregi potegowe
szeregi, Analiza Matematyczna 2, Analiza Matematyczna 2
szeregi (1), Analiza Matematyczna 2, Analiza Matematyczna 2
25 Szeregi potęgowe i ich zbieżność Własności sumy szeregu potęgowego, Studia, Semestr VI, licencj
Szereg potegowy przyklady
Szereg potegowy przyklady ogarnijtemat.com, SiMR inżynierskie, Semestr 2, Równania różniczkowe, Wykł
Szeregi potęgowe pwt wiadomosci
więcej podobnych podstron