Wykład Matematyka doc. Andrzej Drozdowicz

Ekstrema funkcji

Twierdzenia Rolle'a o wartości średniej:

Jeżeli funkcja y=f(x):

1. Jest ciągła w przedziale <a,b>

2. Jest różniczkowalna w przedziale (a,b)

3. Na końcach przedziału ma takie same wartości f(a)=f(b)

To wewnątrz przedziału (a,b) istnieje co najmniej jeden punkt c taki, że f'(c)=0

Geometryczna teza tego twierdzenia mówi, że wewnątrz przedziału (a,b) istnieje taki punkt c, w którym styczna jest równoległa do osi OX (na rys. są 3 takie punkty)

Twierdzenie Rolle'a zapewnia, że w przedziale (a,b) istnieje punkt c, dla którego f'(c)=0 takich punktów może być kilka a nawet nieskończenie wiele

Funkcja jest ciągła

Funkcja jest różniczkowalna

Oraz f(0)=f(π)=0

Z twierdzenia wynika, że w przedziale (0,π) istnieje punkt c taki, że f'(c)=0. Takim punktem jest c= π/2, bo f'(x)=cos(x) a cos(π/2)=0

Twierdzenie Lagrange'a

Jeżeli funkcja y=f(x):

1. Jest ciągłą w przedziale <a,b>

2. Jest różniczkowalna w przedziale (a,b)

To wewnątrz przedziału a,b jest taki punkt c, który:

Geometrycznie teza tego twierdzenia mówi, że w przedziale a,b istnieje co najmniej jeden taki punkt c, w którym styczna jest równoległa do siecznej łączącej punkty A i B (na rysunku są 2 takie punkty)

Z tezy tego twierdzenia wynika, że:

Niech:

Wynika z tego, iż:

1. Jeżeli
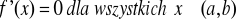
   to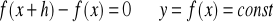
   

2. Jeżeli
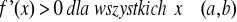
   to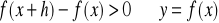
   rośnie

3. Jeżeli
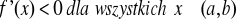
   to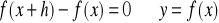
   maleje

Natomiast w skrócie:

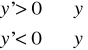
4. Jeżeli w otoczeniu punktu punktu x₀ pierwsza pochodna funkcji zmienia znak z ,,+” na ,,-„ to funkcja w tym punkcie osiąga maksimum

5. Jeżeli w otoczeniu punktu punktu x₀ pierwsza pochodna funkcji zmienia znak z ,,-” na ,,+„ to funkcja w tym punkcie osiąga minimum

Są to tzw warunki dostateczne istnienia ekstremum funkcji

Niech y=f(x) będzie funkcją określoną w pewnym otoczeniu punktu x₀

Maksimum lokalne	Minimum lokalne
Jeżeli istnieje taka dodatnia liczba , taka, że dla każdego: spełnione są warunki:
jeżeli
to
Maksimum właściwe	Minimum właściwe

Twierdzenie Fermata

Jeżeli y=f(x) ma w x₀ ekstremum to ma w tym punkcie pierwszą pochodną = 0

Jest to warunek konieczny istnienia ekstremum funkcji f'(x₀)=0 rozwiązując to równanie znajdujemy punkty ,,podejrzane” o ekstremum tzn. takie, w których funkcja ekstremum może mieć lecz nie musi. O tym czy w punkcie x₀ ,,podejrzanym” o ekstremum funkcji ekstremum posiada rozstrzyga warunek dostateczny istnienia ekstremum

Twierdzenie (reguła) de l'Hospitala [delopitala]

1. Jeżeli funkcje
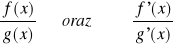
   są określone w pewnym otoczeniu punktu x₀

2. Jeżeli
   

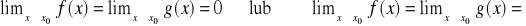
3. Jeżeli istnieje granica
   

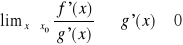
To istnieje

UWAGA:

reguła ta służy do obliczania granic funkcji w przypadku nieoznaczoności typu

Przykłady:

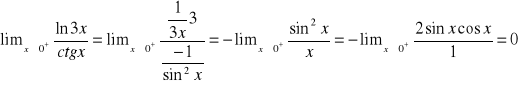
W przypadku nieoznaczoności typu:
można sprowadzić do nieoznaczoności
w następujący sposób:

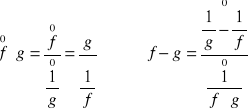
W przypadku
mamy:

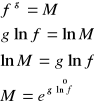
Obliczyć granicę

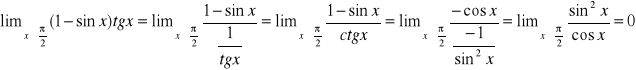
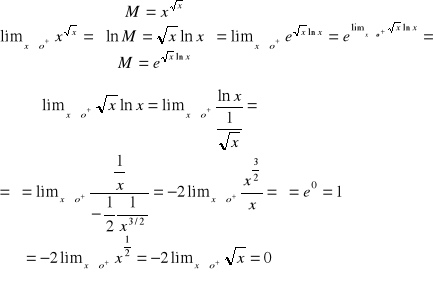
Matematyka wykład doc. Andrzej Drozdowicz 01.12.2009r.

---