Wiadomości wstępne, pojęcia i zadania rachunku wyrównawczego

Niech
będą wynikami pomiarów tej samej wielkości X. W zasadzie tylko jedno z tych spostrzeżeń wystarczy do wyznaczenia jej wartości przykładowo
. Nie jest jednak niczym uzasadnione przyjęcie właśnie
jako wartości X, zwłaszcza, jeżeli wszystkie pomiary zostały wykonane z tą samą dokładnością. Oznacza to, że przy większej ilości spostrzeżeń, niż to jest konieczne, trudno jest zadecydować, którą wartość należy przyjąć jako wynik końcowy dla wyznaczenia szukanej wielkości; jednakże wyniki pomiarów nadliczbowych dają kontrolę otrzymanych spostrzeżeń, która jest nie tylko cenna, ale i wymagana. W przypadku n - krotnych, jednakowo dokładnych pomiarów tej samej wielkości X obiera się za jej wartość średnią arytmetyczną, obliczoną według wzoru:

tzn. nie wynik któregokolwiek z pomiarów, lecz sumę wszystkich ich, podzieloną przez ilość. Obliczona wartość x nie będzie oczywiście równa prawdziwej wartości X, o czym można się przekonać, obliczając średnie z niejednakowo licznych spostrzeżeń. Będzie ona natomiast obliczona w sposób jednoznaczny z danej grupy wyników pomiarów, co jest już jej ważną zaletą. Innym prostym przykładem zagadnienia wyrównawczego jest uzgadnianie wyników pomiarów kątów trójkąta płaskiego. Do wyznaczenia wielkości tych kątów wystarczy zmierzyć dwa, ponieważ trzeci oblicza się z sumy wszystkich trzech kątów. Ewentualna omyłka przy pomiarze nie będzie w takim przypadku zauważona. Natomiast, jeżeli zmierzymy wszystkie trzy kąty, to wówczas skontrolujemy otrzymane spostrzeżenia, ale jednocześnie przekonamy się, że suma wartości zmierzonych kątów będzie się różnić od teoretycznej. Powstaje znowu pewna trudność w określeniu, jakie wartości należy przypisać poszczególnym kątom. W tym prostym przykładzie przyjmuje się je równe spostrzeżeniom poprawionym o jedną trzecią otrzymanej odchyłki.

Obliczenie średniej arytmetycznej jest najprostszym przykładem obliczeń przeprowadzanych w rachunku wyrównawczym. Różnica v między średnią arytmetyczną x a spostrzeżeniem L:

jest błędem pozornym spostrzeżenia L. Wielkość v może być też nazwana poprawką spostrzeżenia, zwłaszcza, jeżeli poprzedni związek napiszemy w formie:

Spostrzeżenia uzupełnione poprawkami otrzymanymi w toku wyrównania nazywamy spostrzeżeniami wyrównanymi. Głównym celem rachunku wyrównawczego jest takie wyznaczenie wartości spostrzeżeń wyrównanych, aby można je było uważać za wartości najbardziej prawdopodobne. Wartość najbardziej prawdopodobną według rachunku prawdopodobieństwa można tylko wtedy uzyskać, gdy wartości, z których ma być wyznaczona, występują ze ściśle określonymi prawdopodobieństwami i według ściśle określonego prawa, zwanego rozkładem prawdopodobieństw. Błędy pozorne spostrzeżeń podlegają tylko w przybliżeniu prawu błędów przypadkowych, które jest rozkładem normalnym prawdopodobieństw. Wobec tego spostrzeżenia wyrównane będą tylko zbliżone do wartości najbardziej prawdopodobnych mierzonych wielkości. Wiąże się z tym drugie zadanie rachunku wyrównawczego, a mianowicie ocena dokładności zarówno wykonanych spostrzeżeń, jak i wielkości z nich obliczonych, bardzo istotna we wszelkich pracach technicznych wymagających odpowiednio dokładnego i ekonomicznego wykonania. Reasumując, zadaniem rachunku wyrównawczego jest:

1) wyznaczanie poprawek spostrzeżeń wykonanych w większej ilości niż to było potrzebne. Poprawki te powinny mieć wartości najbardziej prawdopodobne;

2) określenie dokładności każdego spostrzeżenia oraz dokładności wartości uzyskanych z wyrównania i ich funkcji,

3) upewnienie się, że otrzymane wyniki mają wartości dokładniejsze niż można by je uzyskać inną metodą,

4) podanie sposobów kontroli wykonywanych obliczeń:

5) uzyskanie wzorów empirycznych na podstawie wykonanych w tym celu spostrzeżeń; zadanie to ma szczególne znaczenie w pracach badawczych.

Metoda najmniejszych kwadratów

Przejdziemy z kolei do omówienia metody, na podstawie, której wyznacza się poprawki spostrzeżeń. Spośród kilku teorii ugruntowała się metoda najmniejszych kwadratów. Metoda ta, ustanowiona przez C. F. Gaussa w 1796 r. oraz przez A. M. Legendre'a w 1805 r. jest umową na podstawie, której wykonane spostrzeżenia tak poprawiamy, żeby suma v poprawek tych spostrzeżeń była jak najmniejsza. C. F. Gauss wyprowadził metodę najmniejszych kwadratów na podstawie trzech następujących założeń:

1) wyrównane spostrzeżenia powinny być najbardziej prawdopodobnymi wartościami mierzonych wielkości,

2) błędy średnie wyznaczonych wielkości powinny być mniejsze od otrzymanych jakąkolwiek inną metodą, co jest równoznaczne z tym, że ich wagi powinny być jak największe

3) najbardziej prawdopodobną wartością powinna być średnia arytmetyczna.

Założenia te będą spełnione wówczas, jeżeli poprawki przydzielane spostrzeżeniom będą mieć wartości najbardziej prawdopodobne, ponieważ tylko wtedy wyrównane wielkości są najbardziej prawdopodobne, wyznaczane poprawki mają w przybliżeniu te same własności jak błędy prawdziwe tzn. prawdopodobieństwo ich występowania można obliczyć na podstawie prawa błędów.

Zakładając, że spostrzeżenia
są niejednakowo dokładne, tzn., że należą do różnych szeregów spostrzeżeń, o parametrach
(patrz S_5_Błędy_geodezja ), obliczamy prawdopodobieństwo tego, że spostrzeżeniu
należy przydzielić poprawkę o wartości
:

Prawdopodobieństwo tego, że spostrzeżenie
, powinno otrzymać poprawkę
, jest równe:

. Analogicznie

Prawdopodobieństwo
, że dany szereg niejednakowo dokładnych spostrzeżeń
należy poprawić o wartości
jest równe iloczynowi prawdopodobieństw poszczególnych poprawek, tj.

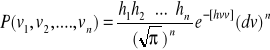
Łatwo zauważyć, że
osiągnie maksimum dla:

Ponieważ kwadraty parametrów h są wprost proporcjonalne do wag p:

,

to podstawowy warunek, który powinny spełniać poprawki spostrzeżeń niejednakowo dokładnych można przedstawić w postaci:

W przypadku równości wszystkich h, a więc i równości wszystkich wag p, za wartości wag można przyjąć jedności. Stąd mamy warunek dla poprawek spostrzeżeń jednakowo dokładnych:

Na podstawie założenia dotyczącego otrzymania najbardziej prawdopodobnych wartości mierzonych wielkości Legendre podał sposób przydzielania poprawek poszczególnym spostrzeżeniom, nazwany metodą najmniejszych kwadratów tj.:

Założenie (drugie) o najmniejszych błędach średnich lub o największych wagach wielkości wyznaczanych za pomocą spostrzeżeń również prowadzi do metody najmniejszych kwadratów. Trzeci warunek, aby średnia arytmetyczna była wielkością najbardziej prawdopodobną prowadzi również do metody najmniejszych kwadratów. W tym celu założymy dwa rodzaje poprawek spostrzeżeń, jedne obliczone z użyciem średniej arytmetycznej
, drugie zaś za pomocą innej wartości, oznaczonej przez
. Poprawki te zestawimy poniżej:

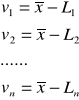
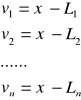
Stąd otrzymujemy:

.

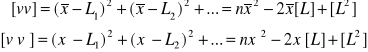
Po odjęciu pierwszej sumy od drugiej otrzymamy:

.

Po podstawieniu za
wartości wynikającej z założenia
:

.

Ostatnie wyrażenie jest zawsze dodatnie, czyli nierówność

.

jest spełniona dla każdej wartości
. Stąd stwierdzamy, że suma kwadratów odchyleń od średniej arytmetycznej jest zawsze mniejsza od sumy kwadratów odchyleń od jakiejkolwiek innej wartości. Można, więc powiedzieć, że założenie o średniej arytmetycznej jako najbardziej prawdopodobnej wartości oraz metoda najmniejszych kwadratów zastosowana do spostrzeżeń dotyczących jednej wielkości są ze sobą równoważne. Metoda najmniejszych kwadratów jest bardziej ogólna niż to wynika z założenia o średniej arytmetycznej i odnosi się ona do wyrównania wszystkich spostrzeżeń. Dla zaznaczenia, że w rachunku wyrównawczym obliczenia przeprowadza się w oparciu o tą metodę używa się też nazwy „rachunek wyrównawczy według metody najmniejszych kwadratów". Metoda najmniejszych kwadratów jest ogólniejsza niż warunek najmniejszych błędów średnich, czyli największych wag wielkości wyznaczonych z wyrównanych spostrzeżeń. Warunek największych wag ma zastosowanie tylko do spostrzeżeń obarczonych błędami przypadkowymi, natomiast metoda najmniejszych kwadratów jest warunkiem matematycznym, którym można się posługiwać przy wyrównaniu spostrzeżeń obarczonych i innymi błędami. Jest to warunek pozwalający na otrzymanie jednoznacznych wyników z danego układu spostrzeżeń wykonanych w ilości większej, niż jest to potrzebne. Cecha jednoznaczności wyników otrzymanych z wyrównania jest jednak niewystarczająca. Wyniki pomiarów powinny przede wszystkim odznaczać się jak największą dokładnością i powinny być jak najbardziej zbliżone do prawdziwych wartości mierzonych wielkości. Metodę najmniejszych kwadratów będziemy stosować do spostrzeżeń obarczonych błędami przypadkowymi, spełniających możliwie najdokładniej prawo błędów Gaussa. W oparciu o powyższe uwagi przedstawimy korzyści wynikające ze stosowania metody najmniejszych kwadratów:

1) jeżeli spostrzeżenia będą spełniały prawo błędów Gaussa, to wówczas wartości otrzymane z ich wyrównania na zasadzie najmniejszych kwadratów będą najbardziej prawdopodobne,

2) w przypadku błędów spostrzeżeń o charakterze przypadkowym metoda najmniejszych kwadratów dostarczy najdokładniejszych wyników;

3) gdyby wyrównywane spostrzeżenia były nawet obarczone błędami nieprzypadkowymi to przy zastosowaniu metody najmniejszych kwadratów otrzymamy jednoznaczne wyniki;

4) obliczenia przeprowadzane według metody najmniejszych kwadratów są proste, otrzymane wzory są symetryczne, w różnych przypadkach wyrównania mają podobny kształt i dają się z łatwością kontrolować;

5) metoda najmniejszych kwadratów łączy się ściśle z rachunkiem prawdopodobieństwa i statystyką matematyczną.

Rodzaje zagadnień rachunku wyrównawczego

W rachunku wyrównawczym spostrzeżenia dzielimy na następujące:

Niezależnie od podanego podziału wyróżnia się spostrzeżenia:

Spostrzeżenia bezpośrednie są wynikami pomiarów szukanej wielkości X. Stosownie do swej nazwy, dotyczą one bezpośrednio wyznaczanych wielkości. Przykładem spostrzeżeń bezpośrednich, jednakowo dokładnych, może być kilkakrotny pomiar długości odcinka AB taśmą stalową. Spostrzeżenia bezpośrednie, niejednakowo dokładne, otrzymuje się z pomiarów różnymi przyrządami lub różnymi metodami.

Spostrzeżenia pośrednie występują wówczas, jeżeli nie możemy bezpośrednio zmierzyć wielkości o szukanych wartościach i z konieczności mierzymy inne, będące ich funkcjami. Wyniki tych pomiarów nazywamy spostrzeżeniami pośrednimi. W ogólnym przypadku spostrzeżenia pośrednie mogą być funkcjami k niezależnych od siebie wielkości X, Y, Z,.... Spostrzeżenia pośrednie zwane są również pośredniczącymi. Nazwa „spostrzeżenia pośredniczące" dobrze oddaje ich funkcję, polegającą na pomiarze wielkości pośredniczących w wyznaczeniu szukanych. Spostrzeżeniami pośrednimi jednakowo dokładnymi są np. wyniki pomiaru kątów mierzonych dla określenia współrzędnych punktów. Przykładem spostrzeżeń pośrednich, niejednakowo dokładnych, są wyniki pomiarów odległości od punktu o wyznaczanych współrzędnych do innych punktów o znanych współrzędnych. Odległości te pozwalają na obliczenie szukanych współrzędnych, a dokładność ich jest zależna od długości zmierzonych odcinków.

Spostrzeżenia zawarunkowane są to wyniki pomiarów wielkości, których prawdziwe wartości są ściśle z sobą związane określonymi równaniami, zwanymi równaniami warunkowymi. Przykładem spostrzeżeń zawarunkowanych, jednakowo dokładnych, są wyniki pomiaru trzech kątów w trójkącie płaskim. Wiemy, że suma prawdziwych wartości tych kątów jest równa
. Spostrzeżeniami zawarunkowanymi niejednakowo dokładnymi są wyniki niwelacji ciągów między kilkoma punktami, tworzącymi w sumie jeden ciąg niwelacyjny zamknięty. Dokładność określenia różnicy wysokości między poszczególnymi punktami uzależniona jest od długości łączących je ciągów.

Spostrzeżenia pośrednie z warunkami są podobnie jak spostrzeżenia pośrednie, wyni­kami pomiarów wielkości służących do wyznaczenia niewiadomych, z tym jednak, że te nie­wiadome mają spełniać znane, ściśle określone warunki.

Spostrzeżenia zawarunkowane z niewiadomymi, podobnie jak spostrzeżenia zawarunkowane są wynikami pomiarów wielkości związanych z sobą równaniami warunkowymi, ale, w których skład wchodzą również pewne nieznane wielkości.

Podział spostrzeżeń na jednakowo i niejednakowo dokładne jest podziałem charakteryzującym spostrzeżenia pod względem ich dokładności. Natomiast podział na spostrzeżenia bezpośrednie, pośrednie itp. jest podziałem uwzględniającym różne sposoby przeprowadzania wyrównań. Na przykład wynik pomiaru długości odcinka będącego przedmiotem pomiaru można uważać za spostrzeżenie bezpośrednie albo też za pośrednie, tj. będące funkcją niewiadomej wielkości. Funkcja ta w danym przypadku jest bardzo prosta, a mianowicie mierzona wielkość l równa się wyznaczonej wielkości. W sieciach triangulacyjnych zmierzone kąty można uznać za pośredniczące w znalezieniu współrzędnych punktów siatki albo można je uważać za spostrzeżenia zawarunkowane, powiązane z sobą różnymi równaniami.

Wyrównania wszystkich rodzajów spostrzeżeń przeprowadza się metodą najmniejszych kwadratów. Natomiast kolejność działań, otrzymywane wzory przy wyrównaniu poszczególnych spostrzeżeń są różne. Uznając, zatem jakieś spostrzeżenia np. za pośrednie wybieramy tym samym tok wyrównania. Wybrany rodzaj wyrównania nie ma wpływu na końcowe wyniki tylko na nakład prac obliczeniowych. Dlatego należy dokładnie poznać wszystkie sposoby wyrównania, by potem móc swobodnie nimi operować.

Techniki rachunkowe

Tok wyrównania wszystkich rodzajów spostrzeżeń wymaga często długich i żmudnych obliczeń. W związku z tym istnieją różne techniki ich przeprowadzania, jak np. rachunek macierzowy, krakowianowy i tensorowy. Sposoby te ułatwiają i znacznie skracają obliczenia. Przy każdym sposobie techniki rachunkowej należy wziąć pod uwagę: ekonomię obliczeń; metody kontroli; metody oceny dokładności otrzymywanych wyników.

Wyrównanie spostrzeżeń bezpośrednich jednakowo dokładnych

Zakładamy, że wielkość, której wartością prawdziwą jest X zmierzono n razy. Jeżeli pomiary wykonano w tych samych warunkach, tą samą metodą oraz za pomocą tych samych przyrządów, to przyjmujemy, że zostały wykonane z tą samą dokładnością.

Ze względu na błędy przypadkowe, którym, jak wiemy, nie jesteśmy w stanie zapobiec, nie możemy wyznaczyć prawdziwej wartości X mierzonej wielkości. W danym przypadku rachunek wyrównawczy ma za zadanie:

a) obliczenie wartości wyrównanej x;

b) określenie dokładności wykonanych spostrzeżeń;

c) określenie dokładności wartości wyrównanej;

d) sprawdzenie wykonanych obliczeń.

a) Obliczenie wartości wyrównanej x.

Oznaczamy: spostrzeżenia symbolami
, poprawki, które zostaną przydzielone tym spostrzeżeniom w toku wyrównania:
; wartość wyrównaną x.

Między spostrzeżeniami, poprawkami spostrzeżeń a wartością wyrównaną zachodzą następujące związki:

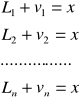
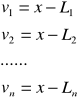
(r1)

Według metody najmniejszych kwadratów suma kwadratów poprawek powinna być równa minimum, czyli

Stąd otrzymujemy:

.

Funkcja
przyjmie wartość minimum, jeżeli pierwsza pochodna
będzie równa zeru, a druga pochodna
będzie dodatnia. Wartości tych pochodnych są następujące:

Przyrównując pochodną
do zera otrzymujemy:

.

Stąd
,

Jeżeli spostrzeżenia L mają duże wartości, to wówczas przyjmiemy przybliżoną wartość niewiadomej
, co pozwoli na operowanie małymi liczbami. Jako wartość
można przyjąć najmniejszy wynik pomiaru.

Równania (r1) przekształcamy wówczas następująco:

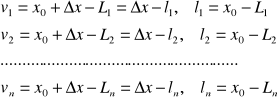
(r2)

Stąd

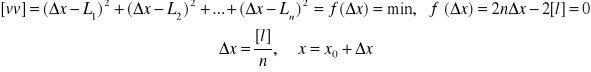
gdzie: x wartość wyrównana, przyjęta przybliżona wartość
,
, l różnica między spostrzeżeniem L a przybliżoną wartością
, n ilość spostrzeżeń.

b) Obliczenie błędu średniego spostrzeżeń. Rozpoczynamy od wyznaczenia poprawek spostrzeżeń v za pomocą równań (r1) albo równań (r2). Następnie podnosimy każdą poprawkę do kwadratu i obliczamy sumę [vv], potrzebną do obliczenia błędu średniego spostrzeżeń

c) Obliczenie błędu średniego . Błąd średni średniej arytmetycznej obliczymy następująco

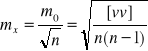
d) Wzory kontrolne. Integralną częścią rachunku wyrównawczego jest oprócz obliczenia wyrównanych wartości błędów średnich również kontrola otrzymanych wyników. W związku z tym wyprowadzamy wzory kontrolne wyrównania spostrzeżeń bezpośrednich, jednakowo dokładnych. Ponieważ

Wzór stanowi pierwszą kontrolę prawidłowego rachunku. Drugą kontrolą jest podwójny sposób obliczania sumy
. Pierwszy z nich polega na podniesieniu poprawek
lub
do kwadratu i na zsumowaniu wyników. Drugim sposobem jest obliczanie sumy
według następującego wzoru:
lub
.

Wyprowadzone wzory zestawimy w kolejności ich stosowania:

;
wartość wyrównana

lub
poprawki spostrzeżeń,

błąd średni spostrzeżenia ;

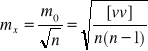
błąd średni wartości wyrównanej;

pierwszy wzór kontrolny,

lub
drugi wzór kontrolny

Przykład. Wyrównanie spostrzeżeń bezpośrednich jednakowo dokładnych - obliczenie wyrównanej długości odcinka AB na podstawie sześciokrotnych wyników jego pomiaru.

Lp.	L (m)	(cm)	v		vv	ll
								+	-
l	120,15	5		2,8	7,84	25
2	120,10	0	2,2		4,84	0
3	120,12	2	0,2		0,04	4
4	120,14	4		1,8	3,24	16
5	120,12	2	0,2		0,04	4
6	120,10	0	2,2		4,84	0
[l] = 13 4,8 4,6 20,84 49

(wartości w polach nie zacienionych są obliczane na podstawie wartości w polach zacienionych,
m wybrano jako minimalną wartość pomiarów L ).

Obliczenie wartości wyrównanej:
,
,
.

Obliczenie poprawek

Błąd średni spostrzeżeń:
.

Błąd średni wartości wyrównanej:
.

Kontrola obliczeń: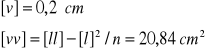
.

Wyniki obliczeń:
.

Wyrównanie spostrzeżeń bezpośrednich niejednakowo dokładnych

Wyrównanie spostrzeżeń bezpośrednich, niejednakowo dokładnych, można przeprowa­dzić tylko wtedy, gdy znany jest wzajemny stosunek ich dokładności, czyli znane są ich wagi. Mając spostrzeżenia niejednakowo dokładne:
o wagach
dotyczące wielkości X, należy obliczyć za pomocą rachunku wyrównawczego:

a) wartość wyrównaną x;

b) błąd średni jednostkowy,

c) błąd średni wartości wyrównanej
;

d) przeprowadzić kontrolę wykonanych obliczeń.

W tym celu zestawiamy związki między spostrzeżeniami, poprawkami spostrzeżeń i war­tością wyrównaną x:

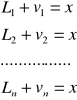
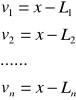
a) Obliczenie wartości wyrównanej x. Obliczenie przeprowadzamy na podstawie warunku
:

.

Warunek
jest spełniony, jeżeli pierwsza pochodna
jest równa zeru, a druga pochodna
jest większa od zera. Wartości tych pochodnych są w tym przypadku nastę­pujące:

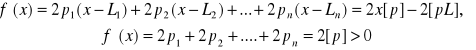
Stąd otrzymujemy:

Powyższe wyrażenie przedstawia wartość wyrównaną, otrzymaną ze spostrzeżeń bezpośrednich, niejednakowo dokładnych. Nazywa się je średnią arytmetyczną ogólną. Można powiedzieć, że:

Jeżeli do obliczeń wprowadzimy przybliżoną wartość
, to wzory przybiorą następującą postać:

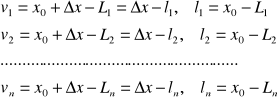
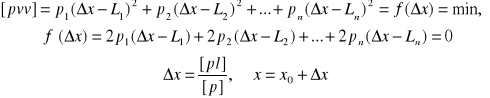
b) Obliczenie błędu średniego jednostkowego. Założone spostrzeżenia są niejednakowo dokładne, więc tym samym odpowiadają im błędy średnie. Spostrzeżeniu o wadze
odpowiada błąd średni jednostkowy
, obliczony na podstawie wzoru:

.

Stanowi on miarę porównawczą dla dokładności spostrzeżeń niejednakowo dokładnych, dlatego obliczamy go zawsze, nawet i wtedy, jeżeli w danym szeregu spostrzeżeń nie znajduje się spostrzeżenie o wadze równej jedności.

c) Obliczenie błędu średniego średniej arytmetycznej ogólnej. Błąd średni wartości wyrównanej, czyli średniej arytmetycznej ogólnej, obliczamy ze wzoru:

.

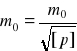
d) Wzory kontrolne. Obliczenia kontrolujemy dwoma wzorami:

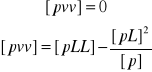
Korzystając z przybliżonej wartości niewiadomej, drugi z podanych wzorów będzie miał ć;

Wyprowadzone wzory zestawimy w kolejności ich stosowania:

;
wartość wyrównana,

lub
poprawki spostrzeżeń;

błąd średni spostrzeżenia;

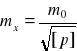
błąd średni wartości wyrównanej;

pierwszy wzór kontrolny;

albo
drugi wzór kontrolny.

Przykład. Wyrównanie spostrzeżeń bezpośrednich niejednakowo dokładnych.

Lp.	Wysokość reperu	Długość ciągu dc	(m)	Hw (m)	p	l (mm)	pl	v	pv	pvv
l 2 3	212,370 214,812 214,621	1,5 2,5 2,0	+0,956 -1,475 -1,298	213,326 213,337 213,323	0,67 0,40 0,50	3 14 0	2,01 5,60 0,00	+1,8 -9,2 4,8	+1,21 -3,68 +2,40	2,16 34,04 11,52
1,57 7,61 -0,1 47,72

(wartości w polach niezacieniowanych są obliczane na podstawie wartości w polach zacieniowanych
to minimalna wartość wysokości węzła W).

Obliczenie wartości l:
, (
,
itp.).

Obliczenie wartości wag p:
, (


).

Obliczenie wartości wyrównanej x:
,
,
.

Obliczenie poprawek:
, (
;
;
)

Błąd średni jednostkowy:

Błąd średni wartości wyrównanej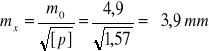
.

Kontrola obliczeń:
;
.

Wynik obliczeń:
.

Wyrównanie par spostrzeżeń

Zakładając dwa niejednakowo dokładne spostrzeżenia
otrzymamy jako wartość wyrównaną średnią arytmetyczną ogólną:

Poprawki obu spostrzeżeń obliczamy według wzorów:

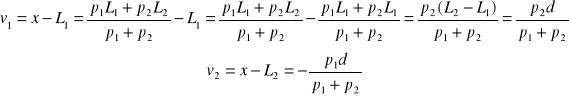
gdzie przez d oznaczono różnicę między dwoma spostrzeżeniami danej pary.

Błąd średni jednostkowy obliczamy, uwzględniając wyrażenia otrzymane na poprawki spostrzeżeń:
;


.

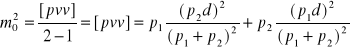
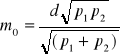
Błąd średni średniej arytmetycznej, obliczonej z pary spostrzeżeń, wynosi:

.

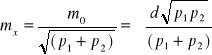
Zestawiając wzory dotyczące jednej pary spostrzeżeń uwzględnimy przypadek jednako i niejednakowej dokładności obu spostrzeżeń.

Para niejednakowo dokładna Para jednakowo dokładna

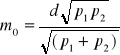
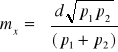
W praktyce wykonuje się dwukrotny pomiar tej samej wielkości, z reguły z tą samą dokładnością, dlatego w dalszych rozważaniach będziemy brać pod uwagę tylko pary składające jednakowo dokładnych spostrzeżeń. Zakładamy, że wykonaliśmy r par spostrzeżeń odnoszących się do wielkości tego samego rodzaju np. długości lub kątów. Na wyrównanie takich obserwacji składają się:

1) obliczenie średnich arytmetycznych z każdej pary, w którego wyniku otrzymujemy
;

2) obliczenie błędów średnich spostrzeżeń każdej pary tj.:

3) obliczenie błędów średnich arytmetycznych każdej pary tj.:
.

Błędy średnie spostrzeżeń, obliczone z każdej pary, nazywamy błędami średnimi spostrzeżeń przed wyrównaniem. Błędy średnie średnich arytmetycznych, otrzymane z każdej pary, nazywamy błędami spostrzeżeń po wyrównaniu.

Na podstawie wiadomości o błędzie średnim wiemy, że obliczenie jego wartości z dwóch spostrzeżeń nie jest wystarczającą oceną dokładności wyników pomiarów. Poprawną ocenę dokładności uzyskuje się dopiero wówczas, jeżeli weźmie się pod uwagę wszystkie pary spostrzeżeń. W tych obliczeniach należy uwzględnić dokładność spostrzeżeń w poszczególnych parach. Dla uproszczenia założymy, że wszystkie pary są jednakowo dokładne. Błąd średni spostrzeżeń wszystkich par można obliczyć np. następująco. Zakładamy, że wykonano r par spostrzeżeń, czyli 2r spostrzeżeń jednakowo dokładnych, których suma [vv] wynosi:

Różnice d są nie tylko różnicami spostrzeżeń, ale zarazem i prawdziwymi wartościami tych różnic; wobec tego do obliczenia błędu średniego zastosujemy wzór, w którym uwzględnia się błędy prawdziwe spostrzeżeń. Ilość tych błędów jest równa ilości par spostrzeżeń. Stąd mamy:

W przypadku par niejednakowo dokładnych obliczamy błąd średni jednostkowy według wzoru

.

Przykład. Wyrównanie jednakowo dokładnych par spostrzeżeń.

Lp.	Spostrzeżenia		Średnia	d	dd
		I				II
l	180° 47' 20"	180° 47' 40"	180° 47' 30"	-20"	400
2	237° 10' 00"	237° 10' 40"	237° 10' 20"	-40"	1600
3	154° 26' 40"	154° 26' 20"	154° 26' 30"	+20"	400
4	171° 28' 00"	171° 28' 40"	171° 28' 20"	-40"	1600
5	130° 55' 20"	130° 55' 00"	130° 55' 10"	+20"	400
6	103° 43' 20"	103° 43' 00"	103° 43' 10"	+20"	400
					4800

Błąd średni spostrzeżeń
.

Przykład. Wyrównanie niejednakowo dokładnych par spostrzeżeń.

Lp.	Spostrzeżenia		Średnia	p	d	pd	pdd
		I						II
1	2,385 m	2,371 m	2,378 m	0,50	+14	+7,00	98,00
2	3,254	3,278	3,266	0,28	-24	-6,72	161,28
3	1,101	1,107	1,104	1,00	- 6	-6,00	36,00
4	0,582	0,578	0,580	2,00	+ 4	+8,00	32,00
5	4,563	4,574	4,568	0,66	-11	-7,26	79,86
6	1,581	1,578	1,580	2,00	+ 3	+6,00	18,00
							425,14

Błąd średni jednostkowy
.

13

Obliczenia związane z uzgadnianiem ze sobą wyników pomiarów wykonanych w większej ilości niż zachodziła potrzeba, są przedmiotem rachunku wyrównawczego.

bezpośrednie, pośrednie, zawarunkowane (warunkowe), pośrednie z warunkami, zawarunkowane, z niewiadomymi.

jednakowo dokładne, niejednakowo dokładne.

Suma iloczynów kwadratów poprawek spostrzeżeń i odpowiadających im wag powinna być jak najmniejsza.

Metoda najmniejszych kwadratów jest podstawą obliczeń w rachunku wyrównawczym.

Spostrzeżenia bezpośrednie są to wyniki pomiarów wielkości wyznaczanych

tj. wartość x otrzymana z wyrównania spostrzeżeń bezpośrednich jednakowo dokładnych jest średnią arytmetyczną obliczoną ze wszystkich spostrzeżeń.

wartość wyrównana x otrzymana za pomocą spostrzeżeń bezpośrednich niejednakowo dokładnych jest równa sumie iloczynów wag i spostrzeżeń, podzielonej przez sumę wag.

R₁

R₂

R₃

W

Δh₃

Δh₂

Δh₁

R₁

Obliczenie wysokości punktu węzłowego

z trzech ciągów niwelacyjnych

Kierunek strzałek jest zgodny z kierunkiem spływu wody

Dwa bezpośrednie spostrzeżenia tej samej wielkości nazywamy parą spostrzeżeń.

---