21.04.2009r.
1. CEL ĆWICZENIA:
Celem ćwiczenia jest wyznaczenie małych oporów kilkoma sposobami. Spotykamy tu również mostek Wheatstone'a, którego zasadę działania poznaliśmy we wcześniejszym ćwiczeniu. Ćwiczenie to zapoznaje nas także z prawami Kirchhoffa i Ohma.
2. OPIS TEORETYCZNY ĆWICZENIA:
Ćwiczenie nr 33
WYZNACZANIE MAŁYCH OPORÓW METODĄ PORÓWNYWANIA
I. Prąd elektryczny.
Prądem elektrycznym nazywamy uporządkowany ruch nośników prądu. Nośnikami prądu mogą być elektrony, dziury (czyli puste miejsca po elektronach) oraz jony. Do tego, aby popłynął prąd potrzebne jest pole elektryczne wytworzone przez źródło prądu (np. baterię).
Kierunek prądu jest umownie oznaczany jako ten przeciwny do kierunku poruszania się elektronów.
Wielkości, które opisują prąd elektryczny to:
Natężenie prądu - ilość ładunku elektrycznego q przepływającego przez poprzeczny przekrój przewodnika w określonym czasie t. Zapisuje się to wzorem:
![]()
.
Jednostką natężenia prądu jest Amper. Jest to podstawowa jednostka układu SI.
Gęstość prądu - jest to stosunek natężenia prądu I do pola poprzecznego przekroju S przewodnika. Zapisuje się to wzorem:
![]()
.
II. Prawo Ohma.
Prawo Ohma dotyczy przepływu prądu stałego przez przewodnik i jest sformułowane na wiele sposobów.
Mówi ono na przykład o tym, że stosunek napięcia U do natężenia I prądu jest stały i zależy tylko od właściwości przewodnika, co zapisujemy w następujący sposób:
![]()
,
gdzie stałą R nazywamy oporem przewodnika.
Inne równoważne sformułowanie tego prawa mówi, że opór rozważanego przewodnika jest zawsze taki sam, niezależnie od wartości przyłożonego napięcia.
Jak widać, z powyższych sformułowań wynika zatem, że wykres zależności natężenia prądu od napięcia jest liniowy.
Warto ustalić jednostkę oporu R. Jednostką tą w układzie SI jest 1 Ω (1 om). Mówimy, że przewodnik ma opór 1 Ω, gdy płynący przez niego prąd o natężeniu 1 A wywoła na jego końcach napięcie 1 V.
Charakterystyczne dla prawa Ohma jest to, że wiele przewodników spełnia je bardzo dokładnie, natomiast inne nie spełniają go w ogóle.
III. Opór właściwy i przewodność właściwa.
Opór przewodnika, zdefiniowany powyżej, zależy od rodzaju materiału, z jakiego jest zbudowany i od jego rozmiarów. Dokładniej, opór jest wprost proporcjonalny do długości przewodu l i odwrotnie proporcjonalny do poprzecznego przekroju przewodu S. Zatem można to zapisać następująco:
![]()
, gdzie
współczynnik proporcjonalności![]()
jest tak zwanym oporem właściwym substancji. Jego jednostką jest ![]()
.
Częściej posługujemy się jednak wielkością nazywaną przewodnością właściwą przewodnika i oznaczaną literką ![]()
. Jest ona powiązana z oporem właściwym wzorem:
![]()
.
Jednostką ![]()
w układzie SI jest (![]()
)-1.
Opór właściwy i przewodność właściwą dla danych przewodników, można odczytać z odpowiednich tablic.
IV. Prawa Kirchoffa.
Kolejnymi ważnymi prawami dotyczącymi przepływu prądu są prawa Kirchoffa.
Aby opowiedzieć o pierwszym prawie Kirchoffa, najpierw powinnam wyjaśnić, co to jest rozgałęzienie. Rozgałęzieniem będę nazywała punkt, w którym zbiega się kilka gałęzi, a dokładniej do którego wchodzą jakieś gałęzie i z którego jednocześnie wychodzą gałęzie. Należy się jeszcze umówić, że natężenie prądu płynącego do rozgałęzienia jest dodatnie, a wypływające z rozgałęzienia jest ujemne. I Prawo Kirchoffa w takim przypadku brzmi następująco: Dla każdego punktu rozgałęzienia suma natężeń prądów we wszystkich gałęziach jest równa 0. Można to zapisać następująco:
![]()
Żeby poznać II Prawo Kirchoffa należy najpierw znać zasady obchodzenia przewodnika z prądem. II Prawo Kirchoffa dotyczy warunków jakie panują w obwodach zamkniętych. Obierzmy dodatni kierunek obchodzenia oczka (obwodu zamkniętego) zgodny z ruchem wskazówek zegara. Natężenie prądów płynących zgodnie z obranym przez nas dodatnim kierunkiem bierzemy ze znakiem +, prądy płynące w kierunku przeciwnym ze znakiem -. Dobieramy również znaki dla sił elektromotorycznych następująco: jeżeli prąd wytwarzany przez źródło siły elektromotorycznej jest zgodny z kierunkiem obchodzenia oczka, wtedy dajemy jej znak -, a tym, które wytwarzają prąd w kierunku przeciwnym niż kierunek obchodzenia oczka, dajemy znak +. Wówczas II Prawo Kirchoffa brzmi: suma iloczynów natężeń prądów w odpowiednich gałęziach obwodu przez ich opory i suma sił elektromotorycznych występujących w poszczególnych gałęziach równa się zero. Można je zapisać następującym wzorem:
![]()
.
V. Łączenie oporników.
Dzięki powyższym prawom, łatwo obliczyć opór zastępczy, gdy mamy połączone oporniki szeregowo lub równolegle. Sposoby te przedstawiają poniższe rysunki schematyczne:
![]()
Połączenie szeregowe
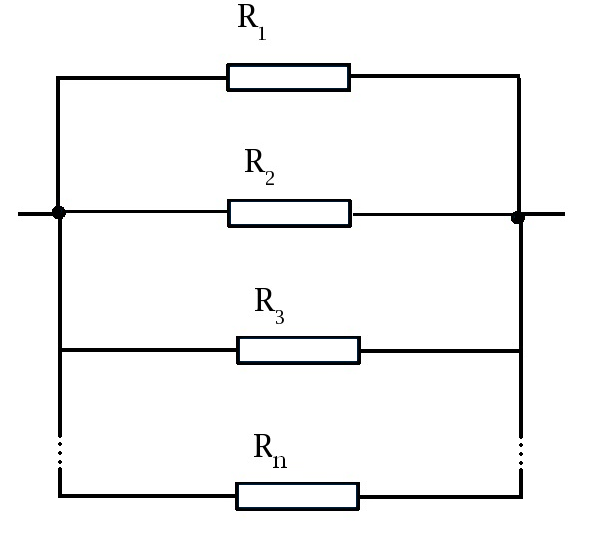
Połączenie równoległe
Przy szeregowym łączeniu oporników przez każdy opornik płynie prąd o takim samym natężeniu. Napięcie na końcach całego układu jest natomiast równe sumie napięć na poszczególnych opornikach, czyli:
![]()
Powracając znów do prawa Ohma i stosując je tak samo do oporu zastępczego (R), jak do poszczególnych oporów (R1, R2, …,Rn) mamy:
![]()
oraz ![]()
.
Wykorzystując te wzory otrzymujemy:
![]()
a stąd ![]()
.
Przy równoległym łączeniu oporników do każdego opornika dołożone jest takie samo napięcie. Wiadomo również, że żadne ładunki nie gromadzą się po drodze z jednego rozgałęzienia do drugiego. Zatem natężenie prądu w rozgałęzieniu jest równe sumie natężeń prądu przepływających przez poszczególne oporniki, czyli:
![]()
.
Pamiętając jednak o prawie Ohma, możemy je zastosować do oporu zastępczego (R) oraz do wszystkich oporów w obwodzie (R1, R2, …,Rn) następująco:
![]()
oraz ![]()
.
Wykorzystując zatem wszystkie te wzory otrzymujemy:
![]()
a stąd ![]()
.
3. LITERATURA:
Edward Purcell; „Elektryczność i magnetyzm”; Państwowe Wydawnictwo Naukowe; Warszawa 1971; rozdziały: 4.3;
David Halliday, Robert Resnick; „Fizyka 2”; Państwowe Wydawnictwo Naukowe; Warszawa 1993; rozdziały: 31-3, 31-4, 31-5;
Szczepan Szczeniowski; „Fizyka Doświadczalna. Część III: Elektryczność i magnetyzm”; Państwowe Wydawnictwo Naukowe; Warszawa 1966; rozdziały: III-36, 37;
4. OPIS WYKONANIA POMIARÓW:
Ćwiczenie rozpoczęłyśmy od zestawienia układu według następującego schematu:
Następnie opiekun ćwiczenia sprawdził połączenie i ustawił wartość oporu R na opornicy suwakowej. Na oporniku dekadowym ustawiłyśmy wartość 6 Ω. Później włączyłyśmy zasilanie i ustawiłyśmy napięcie 3 V. Następnie zamknęłyśmy obwód przełącznikiem K i przełącznikiem W zmieniłyśmy ustawienie układu tak, by miliwoltomierz mierzył spadek napięcia na oporze Ry. Zapisałyśmy tę wartość jako Uy. Później zmieniłyśmy klucz w taki sposób, by miliwoltomierz mierzył spadek napięcia na oporze Rz. Zapisałyśmy tę wartość jako Uz. W ten sam sposób powtórzyłyśmy pomiary dla pozostałych 9 danych nam oporników Ry. Następnie policzyłyśmy wartości nieznanego oporu Ry ze wzoru:
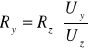
.
Następnie na opornicy dekadowej dla danych oporów ustawiałyśmy wartości jak najbliższe z dokładnością do 1 Ω. Dla każdego oporu Ry ustawiałyśmy jedną większą i jedną mniejszą wartość, dokładnie tak samo jak w poprzedniej części tego ćwiczenia mierząc spadki napięć na odpowiednich oporach.
Ostatnia część ćwiczenia polegała na zmierzeniu naszych nieznanych oporów mostkiem Wheatstone'a.
Wszystkie wyniki przedstawione są w tabelach w dalszej części tego raportu.
5. OPRACOWANIE WYNIKÓW:
Poniżej przedstawiam tabele zawierające wyniki naszych pomiarów:
Tabela 1.
Wyniki pomiarów części pierwszej ćwiczenia.
Ry |
Uy [mV] |
Uz [mV] |
R1 |
153,3 |
139,4 |
R2 |
234 |
136,7 |
R3 |
604 |
119,9 |
R4 |
1424 |
83,1 |
R5 |
462 |
125,9 |
R6 |
201 |
56,9 |
R7 |
1040 |
100,1 |
R8 |
423 |
127,8 |
R9 |
659 |
117,2 |
R10 |
784 |
111,6 |
Tabela 2.
Wyniki pomiarów drugiej części ćwiczenia.
|
OPÓR WIĘKSZY |
OPÓR MNIEJSZY |
||||
Ry |
Rz [Ω] |
Uy [mV] |
Uz [mV] |
Rz [Ω] |
Uy [mV] |
Uz [mV] |
R1 |
7 |
161,2 |
152,1 |
6 |
139,5 |
153,2 |
R2 |
11 |
239 |
226 |
10 |
219 |
227 |
R3 |
31 |
532 |
525 |
30 |
517 |
528 |
R4 |
103 |
1005 |
1015 |
102 |
999 |
1018 |
R5 |
23 |
432 |
426 |
22 |
415 |
422 |
R6 |
212 |
1253 |
1269 |
211 |
1250 |
1271 |
R7 |
63 |
809 |
808 |
62 |
799 |
811 |
R8 |
20 |
387 |
388 |
19 |
370 |
390 |
R9 |
34 |
564 |
563 |
33 |
550 |
568 |
R10 |
43 |
656 |
648 |
42 |
643 |
651 |
Tabela 3.
Wyniki pomiarów trzeciej części ćwiczenia:
Ry |
Wartość odczytana na mostku Wheatstone'a [Ω] |
R1 |
6,6622 |
R2 |
11,474 |
R3 |
33,623 |
R4 |
103,94 |
R5 |
22,197 |
R6 |
214,66 |
R7 |
62,976 |
R8 |
20,112 |
R9 |
34,123 |
R10 |
42,5 |
a) PEŁNY TOK OBLICZEŃ:
I część:
Obliczam wartości oporów Ry ze wzoru:
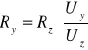
na podstawie wyników z tabeli 1. Oto otrzymane przeze mnie wyniki:
Tabela 4.
Wartości oporów Ry zmierzone w I części tego ćwiczenia.
Ry |
Wartość Ry obliczona w powyższego wzoru [Ω] |
R1 |
6,598278336 |
R2 |
10,27066569 |
R3 |
30,22518766 |
R4 |
102,8158845 |
R5 |
22,01747419 |
R6 |
211,9507909 |
R7 |
62,33766234 |
R8 |
19,85915493 |
R9 |
33,73720137 |
R10 |
42,15053763 |
Następnie obliczam błędy mierzonych wartości napięć. Mierzyłam je multimetrem ustawionym na miliwoltomierz. Używałam zakresów 200 mV, 2V i 20 V. Informacje, gdzie które zakresy zostały ustawione zostały zamieszczone na pierwszej stronie raportu. Jednak ja wszystkie błędy końcowo przedstawię w miliwoltach.
Błędy liczone są z następującego wzoru:
Dla wszystkich zakresów:
![]()
, gdzie:
rdg to wartość otrzymanego pomiaru Uy lub Uz
dgt to wartość ostatniej cyfry odczytu tej wartości
Wyniki liczenia tych błędów przedstawione są w poniższej tabeli:
Tabela 5.
Błędy wartości zmierzonych napięć.
Ry |
ΔUy [mV] |
ΔUz [mV] |
R1 |
0,8665 |
0,797 |
R2 |
2,17 |
0,7835 |
R3 |
4,02 |
0,6995 |
R4 |
8,12 |
0,5155 |
R5 |
3,31 |
0,7295 |
R6 |
20,05 |
0,3845 |
R7 |
6,2 |
0,6005 |
R8 |
3,115 |
0,739 |
R9 |
4,295 |
0,686 |
R10 |
4,92 |
0,658 |
Następnie obliczam błędy wartości obliczonych Ry metodą pochodnej logarytmicznej.
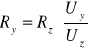
, więc
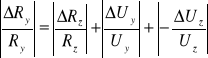
, a stąd: 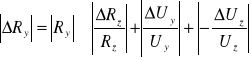
. Wszystkie potrzebne dane mam zebrane w poprzednich tabelach, a ΔRz=1Ω.
Błędy tych wartości wynoszą zatem:
Tabela 6.
Błędy oporów Ry:
Ry |
ΔRy [Ω] |
R1 |
0,9726915447 |
R2 |
1,147786683 |
R3 |
5,415033518 |
R4 |
18,36006725 |
R5 |
3,954898709 |
R6 |
57,89973778 |
R7 |
11,13520246 |
R8 |
3,570938306 |
R9 |
6,040219456 |
R10 |
7,538127721 |
II część:
Obliczam wartości oporów Ry ze wzoru:
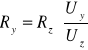
na podstawie wyników z tabeli 2. Oto otrzymane przeze mnie wyniki:
Tabela 7.
Wartości oporów Ry zmierzone w II części tego ćwiczenia:
Ry |
OPÓR MNIEJSZY Ry [Ω] |
OPÓR WIĘKSZY Ry [Ω] |
R1 |
5,463446475 |
7,418803419 |
R2 |
9,647977903 |
11,63274336 |
R3 |
29,375 |
31,41333333 |
R4 |
100,096267 |
101,9852217 |
R5 |
21,63507109 |
23,65714286 |
R6 |
207,5137687 |
209,3270292 |
R7 |
61,08261406 |
63,0779703 |
R8 |
18,02560143 |
19,94845361 |
R9 |
31,95422535 |
34,0603976 |
R10 |
41,48387097 |
43,5308642 |
Następnie obliczam błędy mierzonych wartości napięć. Mierzyłam je tym samym multimetrem i tak samo wszystkie zakresy zapisane są na pierwszej stronie mojego raportu. Wyniki przedstawiam w tabeli:
Tabela 8.
Błędy wartości zmierzonych napięć.
|
OPÓR WIĘKSZY |
OPÓR MNIEJSZY |
||
Ry |
ΔUy [mV] |
ΔUz [mV] |
ΔUy [mV] |
ΔUz [mV] |
R1 |
0,906 |
0,8605 |
0,7975 |
0,866 |
R2 |
2,195 |
2,13 |
2,095 |
2,135 |
R3 |
3,66 |
3,65 |
3,585 |
3,64 |
R4 |
6,025 |
6,075 |
5,995 |
6,09 |
R5 |
3,16 |
3,1 |
3,075 |
3,11 |
R6 |
7,265 |
7,345 |
7,25 |
7,355 |
R7 |
5,045 |
5,04 |
3,995 |
5,055 |
R8 |
2,935 |
2,94 |
2,85 |
2,95 |
R9 |
3,82 |
3,815 |
3,75 |
3,84 |
R10 |
4,28 |
4,24 |
4,215 |
4,255 |
Następnie obliczam błędy wartości obliczonych Ry metodą pochodnej logarytmicznej.
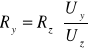
, więc
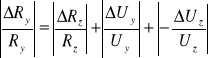
, a stąd: 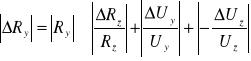
. Wszystkie potrzebne dane mam zebrane w poprzednich tabelach, a ΔRz=1Ω.
Błędy tych wartości wynoszą zatem:
Tabela 9.
Błędy oporów Ry:
Ry |
OPÓR MNIEJSZY ΔRy [Ω] |
OPÓR WIĘKSZY ΔRy [Ω] |
R1 |
0,9726915447 |
1,143496912 |
R2 |
1,147834368 |
1,273994439 |
R3 |
1,385369318 |
1,447845079 |
R4 |
2,180821476 |
2,211955884 |
R5 |
1,303163676 |
1,376231293 |
R6 |
3,387894389 |
3,412676935 |
R7 |
1,671347243 |
1,788054419 |
R8 |
1,223909212 |
1,299867149 |
R9 |
1,402208143 |
1,463269194 |
R10 |
1,530789356 |
1,581189605 |
b) DYSKUSJA BŁĘDÓW I NIEPEWNOŚCI:
Wielkościami mierzonymi w ćwiczeniu są spadki napięć na poszczególnych oporach. Wszystkie te wartości mierzyłyśmy miernikiem uniwersalnym, zatem wartość ich błędów oblicza się z odpowiedniego wzoru, który podałam w punkcie 5a.
Również obarczony błędem jest opór ustawiany na opornicy dekadowej. Dokładność ustawienia oporu wynosi 1 Ω i tyle też jest równy jego błąd.
Błędy mierzonych oporów w ćwiczeniu policzyłam metodą pochodnej logarytmicznej. Wyprowadzenie odpowiedniego wzoru znajduje się także w punkcie 5a.
Na końcu ćwiczenia należało zmierzyć wszystkie badane wcześniej opory mostkiem Wheatstone'a. Błąd takiego pomiaru jest równy dokładności odczytu wartości oporu, czyli równy jest wartości ostatniej cyfry odczytu.
c) PREZENTACJA OTRZYMANYCH WYNIKÓW:
Chciałabym jeszcze przedstawić wszystkie policzone opory wraz z ich błędami w tabelce:
Tabela 10.
Wartości policzonych oporów:
|
I część |
II część |
III część |
|
|
Ry ± błąd [Ω] |
Mniejsze |
Większe |
Ry ± błąd [Ω] |
Ry |
|
Ry ± błąd [Ω] |
Ry ± błąd [Ω] |
|
R1 |
7 ± 1 |
5 ± 1 |
7,4 ± 1,2 |
6,6622 ± 0,0001 |
R2 |
10,3 ± 1,2 |
9,6 ± 1,2 |
11,6 ± 1,3 |
11,474 ± 0,001 |
R3 |
30,2 ± 5,5 |
29,4 ± 1,4 |
31,4 ± 1,5 |
33,623 ± 0,001 |
R4 |
102,8 ± 18,4 |
100,1 ± 2,2 |
102,0 ± 2,3 |
103,94 ± 0,01 |
R5 |
22 ± 4 |
21,6 ± 1,3 |
23,7 ± 1,4 |
22,197 ± 0,001 |
R6 |
212 ± 58 |
207,5 ±3,4 |
209,3 ± 3,5 |
214,66 ± 0,01 |
R7 |
62,3 ± 11,2 |
61,1 ± 1,7 |
63,1 ± 1,8 |
62,976 ± 0,001 |
R8 |
19,9 ± 3,6 |
18,0 ± 1,3 |
19,9 ± 1,3 |
20,112 ± 0,001 |
R9 |
33,7 ± 6,1 |
32,0 ± 1,4 |
34,1 ± 1,5 |
34,123 ± 0,001 |
R10 |
42,2 ± 7,6 |
41,5 ± 1,6 |
43,5 ± 1,6 |
42,500 ± 0,001 |
d) WNIOSKI:
W ćwiczeniu zmierzyliśmy małe opory kilkoma metodami.
Biorąc pod uwagę wielkość błędów możemy wnioskować, że najdokładniejszą metodą jest odczyt z aparatury mostka Wheatstone'a.
Najmniej dokładna jest natomiast metoda wykorzystywana w części I tego ćwiczenia, gdyż do porównywania bierzemy tam przypadkowo dobrany opór, który wartością mocno odbiega od wartości niektórych mierzonych przez nas oporów.
Wiemy jednak, że dokładność pomiaru metodą porównawczą jest największa, jeśli opór badany i ustawiany są najbardziej zbliżone do siebie. Taką własność wykorzystujemy w II części tego ćwiczenia, biorąc możliwie najbardziej zbliżone do wartości mierzonych oporów wartości oporów na oporniku dekadowym.
Nawet licząc i porównując błędy wartości liczonych oporów, zarówno z części I jak i części II łatwo zauważyć, że te z części II są o kilka razy mniejsze, co umacnia nas w twierdzeniu, że metoda zastosowana w części II jest o wiele dokładniejsza od tej w części I.
Sumując, ćwiczenie to pokazało, jak można zwiększyć dokładność metody porównawczej oraz zilustrowało wyższość mostkowej metody pomiaru oporu nad innymi metodami.
602
- 1 -
Wyszukiwarka
Podobne podstrony:
32. WYZNACZANIE OPORU ELEKTRYCZNEGO METODĄ MOSTKA WHEATSTONE'A, Pracownia fizyczna, Moje raporty
39.DRGANIA RELAKSACYJNE, Pracownia fizyczna, Moje raporty
11. WYZNACZANIE MODUŁU YOUNGA METODĄ ZGINANIA PRĘTA, Pracownia fizyczna, Moje przygotowania teoretyc
65. WYZNACZANIE OGNISKOWYCH SOCZEWEK, Pracownia fizyczna, Moje przygotowania teoretyczne
21. WYZNACZANIE WILGOTNOŚCI WZGLĘDNEJ POWIETRZA, Pracownia fizyczna, Moje przygotowania teoretyczne
Wyznaczanie elementów LC metodą rezonansu, Pracownia Zak˙adu Fizyki Technicznej Politechniki Lubelsk
fizyka, Lepkość cieczy-metoda Stokesatom, Pracownia fizyczna
29. WYZNACZANIE WSPÓŁCZYNNIKA ROZSZERZALNOŚCI LINIOWEJ, Pracownia fizyczna, Moje przygotowania teore
2. WYZNACZANIE PRZYSPIESZENIA ZIEMSKIEGO ZA POMOCĄ WAHADŁA RÓŻNICOWEGO, Pracownia fizyczna, Moje prz
47. POMIAR ŁADUNKU KONDENSATORA METODĄ CAŁKOWANIA GRAFICZNEGO, Pracownia fizyczna, Moje przygotowani
45. WYZNACZANIE CHARAKTERYSTYKI PRĄDOWO–NAPIĘCIOWEJ I CZUŁOŚCI INTEGRALNEJ FOTOKOMÓRKI, Pracownia fi
18. WYZNACZANIE PRĘDKOŚCI PRZEPŁYWU CIECZY, Pracownia fizyczna, Moje przygotowania teoretyczne
fizyka, Lepkość cieczy-metoda Stokesa, Pracownia fizyczna
65. WYZNACZANIE OGNISKOWYCH SOCZEWEK, Pracownia fizyczna, Moje przygotowania teoretyczne
54. BADANIE UKŁADÓW PROSTUJĄCYCH (2), Pracownia fizyczna, Moje przygotowania teoretyczne
49. BADANIE REZONANSU NAPIECIA W OBWODZIE LC, Pracownia fizyczna, Moje przygotowania teoretyczne
54. BADANIE UKŁADÓW PROSTUJĄCYCH (1), Pracownia fizyczna, Moje przygotowania teoretyczne
39. DRGANIA RELAKSACYJNE, Pracownia fizyczna, Moje przygotowania teoretyczne
55. BADANIE FOTOOPORU I FOTOOGNIWA, Pracownia fizyczna, Moje przygotowania teoretyczne
więcej podobnych podstron