Temat:

BADANIE DOKŁADNOŚCI

PRZYRZĄDU POMIAROWEGO

Materiały pomocnicze do zajęć laboratoryjnych z metrologii

Zeszyt

BADANIE DOKŁADNOŚCI PRZYRZĄDU POMIAROWEGO

1. CEL ĆWICZENIA.

Ćwiczenie polega na sprawdzeniu dokładności wysokościomierza Trimos. W tym celu zostanie sprawdzona jego wskazania dla wysokości wzorcowych. Tę rolę pełnić będą płytki wzorcowe o wymiarach wskazanych przez prowadzącego. Dla zadanej serii pomiarów należy przeprowadzić test Bartletta, obszar krytyczny oraz wyznaczyć wariancję, przedział ufności na poziomie ufności (1-α) = 95%.

2. WYSOKOŚCIOMIERZ TRIMOS.

Zanim zostanie użyty wysokościomierz należy dokładnie zapoznać się z instrukcją specjalnie do niego przygotowaną. Uruchomić należy po wyraźnej zgodzie prowadzącego laboratorium. Szczególną uwagę należy zwrócić na pokrętło do posuwu suwaka pomiarowego. Jest to bardzo delikatne i czułe urządzenie, które poprzez nieuwagę może ulec zniszczeniu. Uwaga: po dojechaniu końcówki pomiarowej na wymiar mierzony, należy zwolnić sprzęgło, które znajduje się w pokrętle do posuwu suwaka pomiarowego. Kierunek zwalniania sprzęgła jest zgodny z kierunkiem dojazdu końcówki. Np. Jeżeli kręcimy pokrętło w kierunku przeciwnym do wskazówek zegara, czyli końcówka dojeżdża z góry do przedmiotu mierzonego, to w tym samym kierunku zwalniamy sprzęgło.

3. PRZYKŁADOWA TABELA POMIARÓW.

W tabeli przedstawiono wartości wskazane przez badany wysokościomierz Trimos dla płytki wzorcowej o wymiarach „0”, „20”, „40”, „60”, „80”, „100” [mm].

L.p.	Płytka wzorcowa „0”	Płytka wzorcowa „20”	Płytka wzorcowa „40”	Płytka wzorcowa „60”	Płytka wzorcowa „80”	Płytka wzorcowa „100”
-	[mm]	[mm]	[mm]	[mm]	[mm]	[mm]
1	0,001	20,001	39,995	59,920	80,007	100,001
2	0,009	19,996	39,992	59,922	80,001	99,997
3	0,008	19,999	39,994	59,920	80,003	99,997
4	0,010	19,997	39,993	59,919	80,002	99,999
5	0,012	19,995	39,991	59,922	80,002	99,999
6	0,008	19,996	39,996	59,924	80,001	99,998
7	0,012	19,996	39,992	59,922	80,001	100,000
8	0,010	19,992	39,994	59,922	80,003	100,000
9	0,014	19,993	39,994	59,925	80,002	100,000
10	0,012	19,994	39,996	59,923	80,000	100,002
11	0,012	19,993	39,995	59,921	80,001	100,000
12	0,012	19,994	39,995	59,923	80,003	99,997
13	0,008	19,994	39,995	59,921	80,003	99,999
14	0,010	19,996	39,994	59,917	80,001	99,999
15	0,014	19,993	39,994	59,920	80,002	99,997
16	0,010	19,994	39,995	59,920	80,004	99,998
17	0,016	19,992	39,992	59,918	80,003	100,004
18	0,011	19,998	39,994	59,918	80,002	99,998
19	0,011	19,995	39,992	59,918	80,002	99,999
20	0,012	19,996	39,990	59,921	80,002	100,000
21	0,016	19,996	39,994	59,918	80,002	99,999
22	0,012	19,996	39,994	59,921	80,001	99,997
23	0,012	19,998	39,992	59,920	80,001	99,997
24	0,015	19,999	39,994	59,920	80,001	99,996
25	0,014	19,996	39,994	59,920	80,002	99,999
26	0,012	19,994	39,994	59,919	80,000	99,992
27	0,012	19,997	39,994	59,923	80,001	99,996
28	0,010	19,995	39,994	59,920	80,002	99,997
29	0,014	19,996	39,994	59,924	80,001	99,998
30	0,012	19,996	39,994	59,921	80,005	99,998

4. OBLICZENIE WARTOŚCI ŚREDNIEJ.

Wartość średnia dla każdej próby obliczono wg wzoru:

Poniżej przedstawiono wartości średnie dla każdej serii:

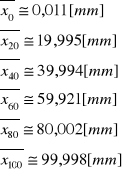
Dolne indeksy oznaczają wartości płytki wzorcowej użytej do pomiaru.

5. WYZNACZENIE WARIACJI I PRZEDZIAŁU UFNOŚCI.

Wariację empiryczną dla każdej próby obliczono korzystając ze wzoru:

1. Płytka wzorcowa „0”

Wartość średniej arytmetycznej:

Lp.
1	0,001	-0,01	1E-4
2	0,009	-0,002	4E-6
3	0,008	-0,003	9E-6
4	0,01	-0,001	1E-6
5	0,012	0,001	1E-6
6	0,008	-0,003	9E-6
7	0,012	0,001	1E-6
8	0,01	-0,001	1E-6
9	0,014	0,003	9E-6
10	0,012	0,001	1E-6
11	0,012	0,001	1E-6
12	0,012	0,001	1E-6
13	0,008	-0,003	9E-6
14	0,01	-0,001	1E-6
15	0,014	0,003	9E-6
16	0,01	-0,001	1E-6
17	0,016	0,005	2,5E-5
18	0,011	0	0
19	0,011	0	0
20	0,012	0,001	1E-6
21	0,016	0,005	2,5E-5
22	0,012	0,001	1E-6
23	0,012	0,001	1E-6
24	0,015	0,004	1,6E-5
25	0,014	0,003	9E-6
26	0,012	0,001	1E-6
27	0,012	0,001	1E-6
28	0,01	-0,001	1E-6
29	0,014	0,003	9E-6
30	0,012	0,001	1E-6

Wartości wariacji empirycznej wynosi: S² = 0,0000083

Wartości kwantyli dla rozdziału
;
.

Model przedziału ufności:

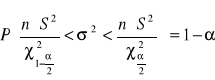
Obliczając lewą i prawą granicę przedziału, otrzymano wartości:

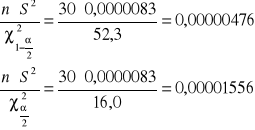
Otrzymano zatem następujący przedział ufności:

P{0,00000476<σ²<0,00001556}=1-α

Poniższy przedział ufności z prawdopodobieństwem 0,95 pokrywa wariację populacji generalnej.

2. Płytka wzorcowa „20”

Wartość średniej arytmetycznej:
.

Lp.
1	20,001	0,006	3,6E-5
2	19,996	0,001	1E-6
3	19,999	0,004	1,6E-5
4	19,997	0,002	4E-6
5	19,995	0	0
6	19,996	0,001	1E-6
7	19,996	0,001	1E-6
8	19,992	-0,003	9E-6
9	19,993	-0,002	4E-6
10	19,994	-0,001	1E-6
11	19,993	-0,002	4E-6
12	19,994	-0,001	1E-6
13	19,994	-0,001	1E-6
14	19,996	0,001	1E-6
15	19,993	-0,002	4E-6
16	19,994	-0,001	1E-6
17	19,992	-0,003	9E-6
18	19,998	0,003	9E-6
19	19,995	0	0
20	19,996	0,001	1E-6
21	19,996	0,001	1E-6
22	19,996	0,001	1E-6
23	19,998	0,003	9E-6
24	19,999	0,004	1,6E-5
25	19,996	0,001	1E-6
26	19,994	-0,001	1E-6
27	19,997	0,002	4E-6
28	19,995	0	0
29	19,996	0,001	1E-6
30	19,996	0,001	1E-6

Wartość wariacji empirycznej wynosi: S² = 0,00000403.

Wartość kwantyli dla rozkładu i model przedziału ufności jak w punkcie 5.1.

Po wykonaniu odpowiednich obliczeń (analogicznie jak w punkcie 5.1) otrzymano następujący przedział ufności:

P{0,00000231<σ²<0,00000756}=1-α

Powyższy przedział ufności z prawdopodobieństwem 0,95 pokrywa wariację populacji generalnej.

3. Płytka wzorowa „40”

Wartość średniej arytmetycznej:
.

Lp.
1	39,995	0,001	1E-6
2	39,992	-0,002	4E-6
3	39,994	0	0
4	39,993	-0,001	1E-6
5	39,991	-0,003	9E-6
6	39,996	0,002	4E-6
7	39,992	-0,002	4E-6
8	39,994	0	0
9	39,994	0	0
10	39,996	0,002	4E-6
11	39,995	0,001	1E-6
12	39,995	0,001	1E-6
13	39,995	0,001	1E-6
14	39,994	0	0
15	39,994	0	0
16	39,995	0,001	1E-6
17	39,992	-0,002	4E-6
18	39,994	0	0
19	39,992	-0,002	4E-6
20	39,99	-0,004	1,6E-5
21	39,994	0	0
22	39,994	0	0
23	39,992	-0,002	4E-6
24	39,994	0	0
25	39,994	0	0
26	39,994	0	0
27	39,994	0	0
28	39,994	0	0
29	39,994	0	0
30	39,994	0	0

Wartość wariacji empirycznej wynosi: S² = 0,00000197.

Wartość kwantyli dla rozkładu i model przedziału ufności jak w punkcie 5.1.

Po wykonaniu odpowiednich obliczeń (analogicznie jak w punkcie 5.1) otrzymano następujący przedział ufności:

P{0,00000113<σ²<0,00000369}=1-α

Powyższy przedział ufności z prawdopodobieństwem 0,95 pokrywa wariację populacji generalnej.

4. Płytka wzorcowa „60”

Wartość średniej arytmetycznej:
.

Lp.
1	59,92	-0,001	1E-6
2	59,922	0,001	1E-6
3	59,92	-0,001	1E-6
4	59,919	-0,002	4E-6
5	59,922	0,001	1E-6
6	59,924	0,003	9E-6
7	59,922	0,001	1E-6
8	59,922	0,001	1E-6
9	59,925	0,004	1,6E-5
10	59,923	0,002	4E-6
11	59,921	0	0
12	59,923	0,002	4E-6
13	59,921	0	0
14	59,917	-0,004	1,6E-5
15	59,92	-0,001	1E-6
16	59,92	-0,001	1E-6
17	59,918	-0,003	9E-6
18	59,918	-0,003	9E-6
19	59,918	-0,003	9E-6
20	59,921	0	0
21	59,918	-0,003	9E-6
22	59,921	0	0
23	59,92	-0,001	1E-6
24	59,92	-0,001	1E-6
25	59,92	-0,001	1E-6
26	59,919	-0,002	4E-6
27	59,923	0,002	4E-6
28	59,92	-0,001	1E-6
29	59,924	0,003	9E-6
30	59,921	0	0

Wartość wariacji empirycznej wynosi: S² = 0,00000393.

Wartość kwantyli dla rozkładu i model przedziału ufności jak w punkcie 5.1.

Po wykonaniu odpowiednich obliczeń (analogicznie jak w punkcie 5.1) otrzymano następujący przedział ufności:

P{0,00000226<σ²<0,00000739}=1-α

Powyższy przedział ufności z prawdopodobieństwem 0,95 pokrywa wariację populacji generalnej.

5. Płytka wzorcowa „80”.

Wartość średniej arytmetycznej:
.

Lp.
1	80,007	0,005	2,5E-5
2	80,001	-0,001	1E-6
3	80,003	0,001	1E-6
4	80,002	0	0
5	80,002	0	0
6	80,001	-0,001	1E-6
7	80,001	-0,001	1E-6
8	80,003	0,001	1E-6
9	80,002	0	0
10	80	-0,002	4E-6
11	80,001	-0,001	1E-6
12	80,003	0,001	1E-6
13	80,003	0,001	1E-6
14	80,001	-0,001	1E-6
15	80,002	0	0
16	80,004	0,002	4E-6
17	80,003	0,001	1E-6
18	80,002	0	0
19	80,002	0	0
20	80,002	0	0
21	80,002	0	0
22	80,001	-0,001	1E-6
23	80,001	-0,001	1E-6
24	80,001	-0,001	1E-6
25	80,002	0	0
26	80	-0,002	4E-6
27	80,001	-0,001	1E-6
28	80,002	0	0
29	80,001	-0,001	1E-6
30	80,005	0,003	9E-6

Wartość wariacji empirycznej wynosi: S² = 0,00000207.

Wartość kwantyli dla rozkładu i model przedziału ufności jak w punkcie 5.1.

Po wykonaniu odpowiednich obliczeń (analogicznie jak w punkcie 5.1) otrzymano następujący przedział ufności:

P{0,00000119<σ²<0,00000388}=1-α

Powyższy przedział ufności z prawdopodobieństwem 0,95 pokrywa wariację populacji generalnej.

6. Płytka wzorcowa „100”

Wartość średniej arytmetycznej:
.

Lp.
1	100,001	0,003	9E-6
2	99,997	-0,001	1E-6
3	99,997	-0,001	1E-6
4	99,999	0,001	1E-6
5	99,999	0,001	1E-6
6	99,998	0	0
7	100	0,002	4E-6
8	100	0,002	4E-6
9	100	0,002	4E-6
10	100,002	0,004	1,6E-5
11	100	0,002	4E-6
12	99,997	-0,001	1E-6
13	99,999	0,001	1E-6
14	99,999	0,001	1E-6
15	99,997	-0,001	1E-6
16	99,998	0	0
17	100,004	0,006	3,6E-5
18	99,998	0	0
19	99,999	0,001	1E-6
20	100	0,002	4E-6
21	99,999	0,001	1E-6
22	99,997	-0,001	1E-6
23	99,997	-0,001	1E-6
24	99,996	-0,002	4E-6
25	99,999	0,001	1E-6
26	99,992	-0,006	3,6E-5
27	99,996	-0,002	4E-6
28	99,997	-0,001	1E-6
29	99,998	0	0
30	99,998	0	0

Wartość wariacji empirycznej wynosi: S² = 0,00000463.

Wartość kwantyli dla rozkładu i model przedziału ufności jak w punkcie 5.1.

Po wykonaniu odpowiednich obliczeń (analogicznie jak w punkcie 5.1) otrzymano następujący przedział ufności:

P{0,00000266<σ²<0,00000869}=1-α

Powyższy przedział ufności z prawdopodobieństwem 0,95 pokrywa wariację populacji generalnej.

6. WYZNACZENIE TESTU BARTLETTA

Test Bartletta polega na porównaniu kilku (większa ilość od 2) wariancji. Zgodnie z założeniami testu Bartletta przyjmuje się co następuje:

1. populacje generalne mają rozkłady normalne
   

2. 
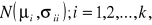
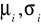
   - nieznane,

3. k prób prostych o liczebności n_i,

4. 
   

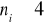
Hipotezy: H₀ :
,

H₁ : nie wszystkie wariancje są równe

Statystyka:

gdzie:

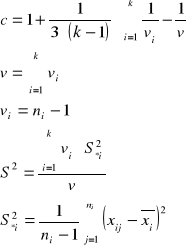
Dla przykładu: k=6, n_i = 30.

Po podstawieniu do powyższych wzorów odpowiednich wartości otrzymano następujące wartości poszczególnych współczynników statystyki M:

- współczynnik c: c = 1,013

- współczynnik v_i: v_i = 29

- współczynnik v: v = 174

- współczynnik S²: S² = 0,000003959 = 3,959E-6

Obliczenie wyrażeń użytych w statystyce:

Lp.	Płytka wzorcowa o wartości
1	0	8,586E-6	2,169	0,774	22,446
2	20	4,172E-6	1,054	0,053	1,537
3	40	2,034E-6	0,514	-0,666	-19,314
4	60	4,068E-6	1,028	0,028	0,812
5	80	2,137E-6	0,540	-0,616	-17,864
6	100	4,793E-6	1,211	0,191	5,539

- wyrażenie

Ostatecznie (po podstawieniu wszystkich wyżej obliczonych współczynników i wyrażeń) otrzymujemy wartość statystyki M:

M₀ = 6,755

1. Wyznaczenie obszaru krytycznego.

Jeżeli hipoteza zerowa H₀ jest prawdziwa, to statystyka M ma asymptotycznie rozkład
o (k-1) stopni swobody.

Obszar krytyczny:

Dla przyjętego poziomu ufności (1-α =0,95) kwantyl rozkładu
ma wartość równą 11,1 - wobec czego obszar krytyczny ma postać:

co oznacza, że nie ma podstaw do odrzucenia hipotezy H₀, czyli nie wykazano również stopnia rozproszenia błędów pomiarowych dla badanych wysokości pomiarowych. Inaczej mówiąc, błąd pomiaru nie zależy od wysokości pomiarowej.

7. ZADANIE POMIAROWE

7.1 Dokonać pomiaru płytek wskazanych przez prowadzącego - tab. 7.1.

1. Zrobić obliczenia wartości średniej.

2. Wyznaczyć wariację i przedział ufności - tab. 7.2.

3. Wyznaczyć test Bartletta i obszar krytyczny - tab. 7.3. Wyciągnąć wnioski

Tabela 7.1.

L.p.	Płytka wzorcowa	Płytka wzorcowa	Płytka wzorcowa	Płytka wzorcowa	Płytka wzorcowa	Płytka wzorcowa
-	[mm]	[mm]	[mm]	[mm]	[mm]	[mm]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Tabela 7.2.

Lp.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Tabela 7.3.

Lp.	Płytka wzorcowa o wartości
1
2
3
4
5
6

1

Zakład Metrologii i Systemów Pomiarowych

Politechnika Poznańska

Pl. Skłodowskiej-Curie 5

61-542 POZNAŃ

tel./fax [phone]

---