Politechnika Śląska
Wydział Elektryczny
Kierunek EiT
Semestr 2, grupa T2
Ćwiczenie laboratoryjne z fizyki :
Badanie szeregowego rezonansu napięciowego.
Sekcja 9
Wojcik Grzegorz
Kożuszek Aleksandra
Wprowadzenie.
Celem ćwiczenia jest wyznaczenie dobroci oraz rezystancji układu rezonansowego. Układ rezonansowy składa się z połączonych szeregowo : cewki indukcyjnej, opornika, kondensatora oraz generatora prądu przemiennego (siła wymuszająca). Prądem przemiennym nazywamy prąd, którego natężenie chwilowe zmienia się w czasie zgodnie z zależnością : gdzie : I0 - natężenie szczytowe [A]; ω - częstość [Hz]; t - czas [s]; φ - faza początkowa.
Przepływem prądu przemiennego, podobnie jak stałego, rządzą prawa Kirchoffa, lecz inaczej niż w obwodzie prądu stałego zachowują się kondensator i cewka. Prąd przemienny przepływa przez kondensator, przy czym przewodzenie prądu polega na ładowaniu kondensatora raz w jednym a za pół okresu przeciwnym kierunku. Napięcie UC na okładkach kondensatora wyraża się wzorem : gdzie : q - ładunek zgromadzony na okładkach kondensatora [C]; C - pojemność kondensatora [F]; ZC - impedancja kondensatora (opór jaki stawia on przepływowi prądu przemiennego) [Ω]; - kąt przesunięcia fazowego, o jaki jest przesunięte napięcie przemienne na kondensatorze w stosunku do natężenia prądu płynącego przez kondensator; . Moduł impedancji wyraża się wzorem : [Ω] .
W zachowaniu się cewki w obwodzie prądu przemiennego istotną rolę spełnia siła elektromotoryczna samoindukcji wyrażona wzorem : gdzie L - współczynnik samoindukcji cewki (cecha charakterystyczna) [H]; ZL - impedancja cewki (opór jaki stawia ona przepływowi prądu przemiennego) [Ω]; - kąt przesunięcia fazowego, o jaki jest przesunięte napięcie przemienne na cewce w stosunku do natężenia prądu płynącego przez cewkę. Moduł impedancji wyraża się wzorem : [Ω] .
Wielkością zwaną impedancją można posługiwać się analogicznie do rezystancji w obwodach prądu stałego. W przypadku obwodu złożonego z szeregowo połączonych opornika, kondensatora oraz cewki moduł impedancji wyraża się wzorem : . Na podkreślenie zasługuje fakt, iż posługiwanie się pojęciem impedancji w obwodach prądu przemiennego umożliwia rozwiązywanie wielu zagadnień poprzez konstrukcję wektorowych wykresów napięć na elementach obwodu RLC.
Związek pomiędzy amplitudą natężenia prądu płynącego przez obwód szeregowy a amplitudą i częstotliwością przyłożonego napięcia wyraża się wzorem : gdzie U0 - napięcie wymuszające. Krzywa będąca wykresem zależności amplitudy natężeń prądu płynącego przez obwód RLC jako funkcję częstotliwości przyłożonego napięcia nosi nazwę krzywej rezonansowej. Amplituda natężenia osiąga wartość maksymalną w warunkach rezonansu, to jest gdy częstotliwość zmian przyłożonego napięcia odpowiada tzw. częstości rezonansowej układu wyrażającej się wzorem : . W warunkach rezonansu spadki napięć na kondensatorze mają jednakowe wartości oraz przeciwne fazy, czyli się znoszą. Moduł impedancji wyraża się wtedy wzorem : gdzie R - opór w układzie RLC. Można więc w warunkach rezonansu wyznaczyć opór układu : .
Jakość układu rezonansowego opisuje tzw. współczynnik dobroci układu Q. Jest to pomnożony przez 2Π stosunek maksymalnej energii zgromadzonej w obwodzie do energii traconej w ciągu jednego okresu. Dobroć układu RLC wyraża się wzorem : . Wartość Q można także określić z przebiegu krzywej rezonansowej : jest ona równa stosunkowi częstotliwości rezonansowej ωR do szerokości połówkowej krzywej mierzonej w dla natężenia .
Opis przebiegu ćwiczenia.
Łączymy obwód według schematu.
Ustalamy parametry początkowe :
pojemność kondensatora C=60 [nF]
indukcyjność cewki L=400 [mH]
napięcie zasilające układ U0 = 3 [V]
Zmieniając częstotliwość generatora co 50 [Hz] w przedziale 200÷2000 [Hz] notujemy wskazania mierników. W otoczeniu rezonansu wykonujemy pomiary co 10 [Hz].
Schemat układu pomiarowego.
Tabela pomiarowa.
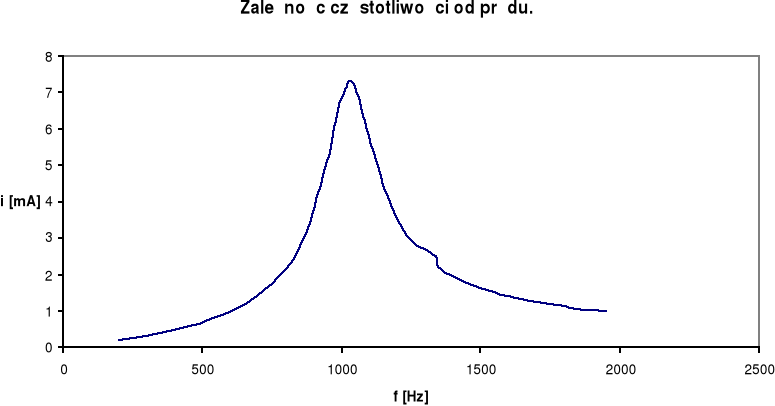
Wykresy.
Opracowanie wyników pomiarów.
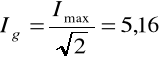
w celu obliczenia dobroci układu metodą szerokości połówkowej, obliczamy :odczytujemy częstotliwości, dla których I=IQ :
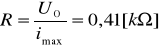
obliczamy rezystancję układu :Korzystając z wyliczonej rezystancji R, obliczamy dobroć układu :
Obliczenia błędu pomiarowego.
Obliczenia dla rezystancji:
Obliczenia dla dobroci metodą szerokości połówkowej:
Obliczenia dla dobroci metodą teoretyczną:
Podsumowanie.
f [Hz] |
i [mA] |
UC [V] |
UL[V] |
200 |
0,2 |
3,22 |
0,12 |
250 |
0,26 |
3,29 |
0,19 |
300 |
0,33 |
3,39 |
0,28 |
350 |
0,40 |
3,50 |
0,39 |
400 |
0,49 |
3,65 |
0,52 |
450 |
0,58 |
3,83 |
0,72 |
500 |
0,67 |
4,05 |
0,95 |
550 |
0,82 |
4,32 |
1,23 |
600 |
0,97 |
4,67 |
1,58 |
650 |
1,16 |
5,10 |
2,02 |
700 |
1,41 |
5,68 |
2,62 |
750 |
1,72 |
6,44 |
3,40 |
800 |
2,16 |
7,49 |
4,50 |
850 |
2,77 |
8,98 |
6,09 |
900 |
3,71 |
11,25 |
8,56 |
950 |
5,13 |
14,60 |
12,38 |
960 |
5,51 |
15,45 |
13,41 |
970 |
5,87 |
16,29 |
14,45 |
980 |
6,20 |
17,01 |
15,39 |
990 |
6,50 |
17,59 |
16,33 |
1000 |
6,84 |
18,31 |
17,28 |
1012 |
7,03 |
18,55 |
17,85 |
1018 |
7,09 |
18,59 |
18,04 |
1029 |
7,30 |
18,90 |
18,78 |
1043 |
7,22 |
18,40 |
18,74 |
1053 |
7,05 |
17,79 |
18,46 |
1062 |
6,84 |
17,08 |
18,03 |
1072 |
6,55 |
16,19 |
17,43 |
1079 |
6,35 |
15,56 |
16,96 |
1089 |
6,06 |
14,72 |
16,32 |
1101 |
5,68 |
13,62 |
15,44 |
1152 |
4,37 |
9,94 |
12,32 |
1199 |
3,53 |
7,67 |
10,29 |
1251 |
2,91 |
6,01 |
8,80 |
1340 |
2,49 |
4,92 |
7,80 |
1346 |
2,21 |
4,18 |
7,09 |
1407 |
1,93 |
3,46 |
6,41 |
1452 |
1,77 |
3,05 |
6,02 |
1500 |
1,62 |
2,69 |
5,66 |
1548 |
1,51 |
2,40 |
5,30 |
1600 |
1,40 |
2,15 |
5,13 |
1650 |
1,32 |
1,94 |
4,93 |
1702 |
1,24 |
1,76 |
4,75 |
1750 |
1,18 |
1,61 |
4,61 |
1802 |
1,12 |
1,47 |
4,47 |
1845 |
1,06 |
1,37 |
4,37 |
1900 |
1,03 |
1,27 |
4,17 |
1950 |
0,99 |
1,16 |
3,97 |
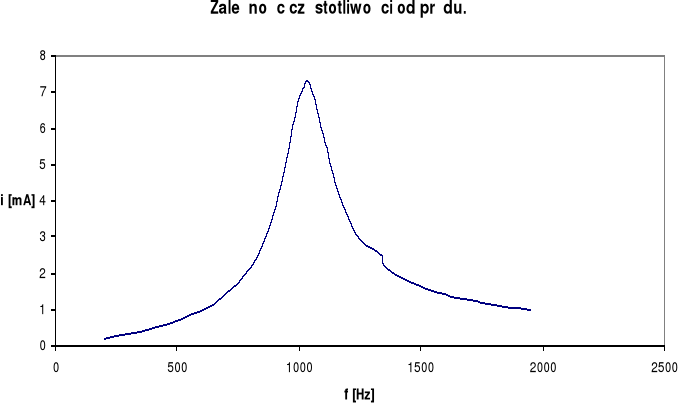
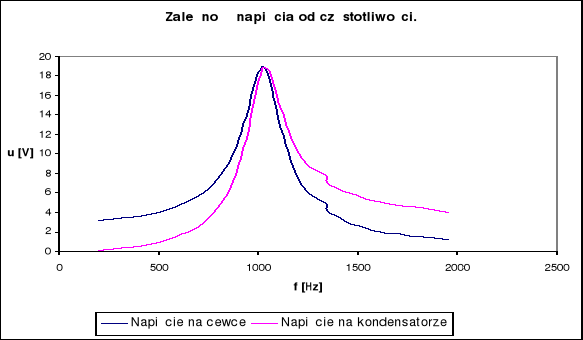
Na podstawie tabeli rysujemy wykres zależności natężenia prądu od częstotliwości oraz zależności napięcia UL i UC od częstotliwości. Z wykresu natężenia prądu w funkcji częstotliwości odczytujemy maksymalne natężenie prądu płynącego w obwodzie IMAX oraz odpowiadającą mu częstotliwość rezonansową fR:
IMAX = 7,30 [mA]
fR = 1029 [Hz]

f1 = 950 [Hz] f2 = 1115 [Hz]
![]()
Δf = 1115-950 = 165 [Hz]
więc :
![]()
Błąd liczę metodą różniczki zupełnej :
Mamy :
U0 = 3 [V]
ΔU0 = 0,5% wskazania = 0,015 [V]
IMAX = 0,0073 [A]
Δ IMAX = 0,0073 = 0,000037 [A]
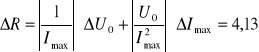
Więc :
czyli
R = 410 ± 4,13 [Ω]
Mamy :
fR = 1029 [Hz]
ΔfR = 0,1% wskazania = 0,1% ⋅ 1029 = 1,029 [Hz]
Δf = 165 [Hz]
Δ (Δf) = 0,2![]()
165 = 0,33 [Hz]
Więc :
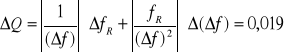
czyli
Q = 6,30 ± 0,02
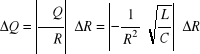
Mamy :
R = 410 [Ω]
ΔR = 4,13 [Ω]
L = 0,400 [H]
C = [F]
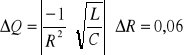
Więc :
czyli
Q = 6,36 ± 0,06
Na podstawie wykonanych przez nas pomiarów otrzymaliśmy następujące wyniki:
Częstotliwość rezonansowa układu wynosi:
fR = 1029 ± 1 [Hz]
Wyliczona rezystancja obwodu rezonansowego wynosi :
R = 410 ± 4,05 [Ω]
Dobroć obwodu wyliczona metodą szerokości połówkowej wynosi :
Q = 6,30 ± 0,02
Dobroć obwodu wyliczona ze wzoru analitycznego wynosi :
Q = 6,36 ± 0,06
Jak widać , dobroć obwodu wyliczona metodą analityczną różni się od dobroci wyznaczonej na podstawie pomiarów, a różnica ta przekracza zakres obliczonych błędów pomiarowych. Na mniejszą, w stosunku do wyliczeń analitycznych, dobroć układu mogły wpłynąć nie uwzględnione w rachunkach pojemności i indukcyjności powstałe na skutek podłączenia mostka LC do obwodu pomiarowego za pomocą przewodów , oraz różnice pomiędzy wartościami wskazywanymi przez mostek, a faktycznymi wartościami pojemności i indukcyjności .
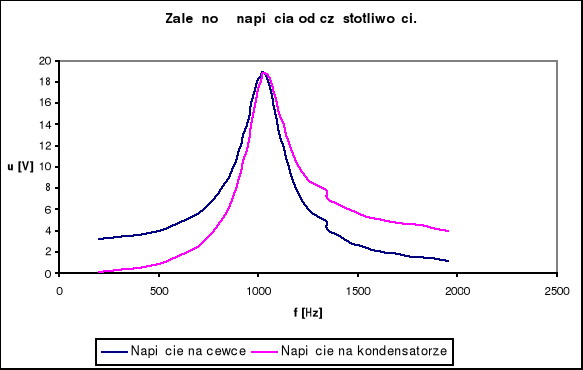
Zależności prądu oraz napięć na kondensatorze i cewce indukcyjnej zostały przedstawione na wykresach . Można zauważyć , że krzywa przedstawiająca Uc = f(f) wyraźnie przypomina krzywą UL = f(f) odbitą symetrycznie względem prostej f = fr , gdzie fr - częstotliwość rezonansowa układu.
- 8 -
![]()
![]()
![]()
![]()
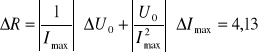
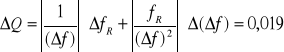
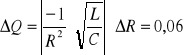
Wyszukiwarka
Podobne podstrony:
WICZENIE8 12 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
WICZENIE8 12 F 2, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki
opracowanie cw 10, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labork
Sprawozdanie lab 10, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, labo
POLARYMETR, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 10 Badanie zj
[10]opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
Nr ćwiczenia, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, 10 Badanie
10 opracowanie, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
10 W EM, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, Laborki
WICZENIE12 4 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
WICZENIE3 7 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, L
WICZENIE10 2 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
10 BARCHNICKI, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, L
10. Dyfrakcja i Polaryzacja - Teoria, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - L
WICZENIE5 9 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, L
WICZENIE9 1 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki,
WICZENIE1 5 F, Elektrotechnika AGH, Semestr II letni 2012-2013, Fizyka II - Laboratorium, laborki, L
więcej podobnych podstron