Politechnika Śląska

Wydział Elektryczny

Kierunek: Elektronika i Telekomunikacja

Semestr II , Grupa T2

SPRAWOZDANIE Z ĆWICZENIA:

Sekcja IX

Kożuszek Aleksandra

Wojcik Grzegorz

1. Wprowadzenie teoretyczne

Każde ciało poruszające się w cieczy doznaje pewnej hamującej siły wskutek tego, że warstewki cieczy przylegające do ciała będącego w ruchu pociągają za sobą coraz dalsze warstewki sąsiednie. Mamy tu do czynienia z przesuwaniem się jednych warstewek cieczy względem drugich. Występuje tu spadek prędkości przylegających cząsteczek cieczy.

Siła która wywołuje ten spadek prędkości, ma swe źródło w przyciąganiu między cząsteczkowym. Jest ona czynnikiem hamującym ruch, przypisujemy jej zatem zwrot przeciwny kierunkowi ruchu i nazywamy ją tarciem wewnętrznym cieczy albo lepkością - w odróżnieniu od tarcia zewnętrznego, z którym mamy do czynienia wówczas, gdy dwie powierzchnie różnych ciał poruszają się względem siebie.

Prawo Stokesa, według którego gładka kulka o promieniu R, poruszająca się w cieczy ze stałą prędkością v doznaje oporu tarcia T skierowanego przeciwnie względem v, wyraża się wzorem:

F_T = - 6πηRv, gdzie η to współczynnik lepkości dynamicznej. Wielkość η jest niezależna od materiału, z którego wykonano kulkę, zależy natomiast od rodzaju cieczy i bardzo silnie od jej temperatury. Ruchy termiczne cząstek mają wpływ na siły oddziaływania między cząsteczkowego. W cieczach wzrost prędkości ruchów termicznych siły te osłabia (η maleje).

Wielkość η jest stała dla danej cieczy i temperatury i nosi nazwę współczynnika lepkości lub tarcia wewnętrznego cieczy. Jeżeli kulka wykonana jest z materiału o gęstości ρ_k większej od gęstości ρ_p płynu, to ruch może następować na skutek działania siły ciężkości: F_g = mg = ρ_kVg = ρ_k 4/3 πR³g.

Ponieważ jednak kulka spada, w ośrodku płynnym działa na nią dodatkowo siła wyporu Fw, która zgodnie z prawem Archimedesa wyraża się wzorem: F_w = - 4/3πR³ρ_pg. Sumując wszystkie siły działające na kulkę otrzymamy: F=Fg+Fw+FT, czyli F = ρ_k 4/3 πR³g - 4/3πR³ρ_pg - 6πηRv.

Spadek kulki w płynie ulega znacznemu zwolnieniu w rurce o średnicy nieznacznie przekraczającej średnicę kulki. Wtedy rurkę musimy ustawić nieco ukośnie, gdyż przy ustawieniu pionowym ruch kulki nie jest jednostajny. Przy ustawieniu skośnym kulka toczy się po ściance rurki. Do omawianego przypadku stosuje się wzór zapisany w postaci: η=K(ρk-ρo)t, gdzie K jest stałą przyrządu, którą wyznaczamy z pomiaru wykonanego dla płynu o znanym współczynniku lepkości. Współczynnik lepkości zależy w dużym stopniu od temperatury. Dla cieczy zależnością tą rządzi prawo: , gdzie T jset temperaturą w skali Kelvina, A i B - stałe charakteryzujące ciecz.

Wiskozymetr Höplera składa się z rurki, w której mierzymy czas spadku kulki, otoczonej płaszczem wodnym. Temperaturę wody regulujemy ultra termostatem. Jeden z korków zamykających rurkę jest wydrążony i zaopatrzony w wentyl. W temperaturze pokojowej wydrążenie to pozostaje puste. W miarę podgrzewania objętość cieczy wzrośnie i wydrążenie wypełnia się, a ciśnienie wzrasta tylko nieznacznie. Pomiar czasu opadania kulki można powtarzać wielokrotnie. Wystarczy każdorazowo obrócić przyrząd o kąt p wokół osi. Śruba znajdująca się z tyłu przyrządu służy do unieruchomienia rurki. Poziomica służy do kontroli ustawienia przyrządu. Jako błąd pomiaru przyjmujemy błąd termometru DT.

Cechą charakterystyczną wiskozymetru H*pplera jest nachylenie rury pomiarowej pod kątem około 10^O. Kulka szklana lub metalowa (zależnie od lepkości cieczy) posiada średnicę bliską średnicy wewnętrznej rury, dzięki czemu wydłuża się czas opadania, a właściwie czas staczania kulki.

Siła oporu ze strony cieczy jest proporcjonalna do prędkości toczenia się kulki:

gdzie k - współczynnik proporcjonalności stały dla danego przyrządu. Rozkładając siły ciężkości i wyporu na składowe otrzymamy warunek równowagi sił:

.

Po przekształceniach otrzymujemy wyrażenie na współczynnik lepkości cieczy:

gdzie
- stała aparaturowa, l - odległość pomiędzy rysami pomiarowymi.

2. Przebieg ćwiczenia

1. Sprawdzamy ustawienie wiskozymetru przy pomocy poziomicy.

2. Zmieniając temperaturę cieczy przy pomocy ultra termostatu z termometrem kontaktowym w granicach od temperatury pokojowej do ok 50[°C] co około 5[°C] mierzymy czas opadania kulki między skrajnymi położeniami obserwacyjnymi.

3. Dla każdej temperatury pomiary powtarzamy trzykrotnie.

3. Obliczenia

1. Dla każdej temperatury obliczamy współczynnik lepkości badanego oleju parafinowego stosując wzór empiryczny:

η=K(ρk-ρo)t,

gdzie K=1.2018*10-6 - stała aparaturowa,

ρk=8150 - gęstość kulki,

o - gęstość oleju (wg danych z tabeli),

t - średnia wartość czasu opadania kulki.

Wyniki obliczeń są zawarte w tabeli poniżej.

2. Obliczamy błąd wyznaczania współczynnika lepkości (oddzielnie dla każdej temperatury, metodą różniczki zupełnej: Dη=K(ρk-ρo)Dt), gdzie Dt to dokładność pomiaru czasu (0.1s). Wyniki obliczeń są zawarte w tabeli.

3. Rysujemy wykres zależności temperaturowej współczynnika lepkości oleju η=η(T).

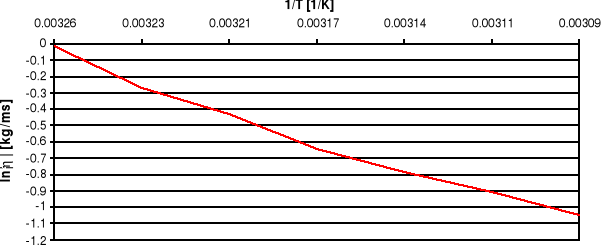
4. Rysujemy wykres zależności . Aby temperaturę wyrazić w Kelwinach należy zastosować wzór T[K] = T[[°C] + 273.

5. Metodą regresji liniowej obliczamy współczynniki A i B wzoru określającego temperaturową zależność współczynnika lepkości:
   ,

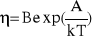
gdzie k=1.38*10-23 - stała Boltzmana.

Wyznaczone współczynniki a i b (y = ax + b, y=η, x=T) wynoszą:

a=-0.0336+-0.0041 , b=2.00+-0.04. Zostały one wyznaczone przy użyciu programu komputerowego.

4. Tabela pomiarowa

lp.	T [°C]	ρo		Tśr [s]	η [kg/ms]	Δη [kg/ms]	ln|η| [kg/ms]	ln|Dη| [kg/ms]
1	33.0	869.0	0,0033	113	0,9888	0,0009	-0,0113	-7,0131
2	36.0	867.5	0,0032	87	0,7614	0,0009	-0,2726	-7,0131
3	39.0	865.5	0,0032	74	0,6478	0,0009	-0,4342	-7,0131
4	42.0	863.0	0,0032	60	0,5255	0,0009	-0,6434	-7,0131
5	45.0	861.2	0,0031	52	0,4555	0,0009	-0,7864	-7,0131
6	48.0	859.5	0,0031	46	0,4030	0,0009	-0,9088	-7,0131
7	51.0	856.7	0,0031	40	0,3506	0,0009	-1,0481	-7,0131

5. Wykresy

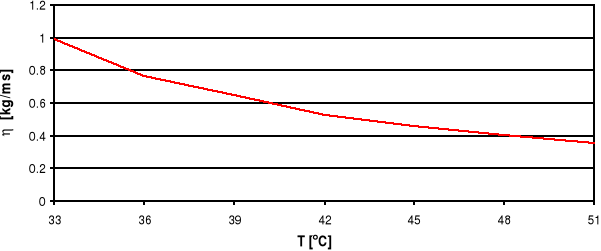
Wykres zależności temperaturowej współczynnika lepkości oleju η=η(T).

Wykres zależności

6. Wnioski

Wraz ze wzrostem temperatury badanego oleju czas opadania kulki maleje. Jest to skutkiem osłabienia siły tarcia wewnętrznego badanej cieczy, która maleje ze wzrostem temperatury. Można się przekonać o słuszności tego stwierdzenia, analizując wartości współczynnika lepkości badanej cieczy dla różnych temperatur. Wartość współczynnika lepkości badanego oleju parafinowego maleje wraz ze wzrostem temperatury (czyli tarcie wewnętrzne maleje). Pomiar czasu opadania kulki wykonywaliśmy trzykrotnie dla każdej temperatury, począwszy od temperatury 33°C. Za pomocą ultratermostatu zwiększaliśmy temperaturę co 3°C, aż do 51°C. Jednak w rzeczywistości każdy pomiar odbywał się dla innej temperatury np. 36.5°C, 36°C, 35.5°C - wskazania termometru dla 33°C w tabeli pomiarowej. Było to związane z ochładzaniem się cieczy, w której znajdował się termometr. Ciecz ta oddawała swoje ciepło do otoczenia o niższej temperaturze.

Uzyskane wyniki są zbliżone do wyników tablicowych, gdzie dla wody o temp. 20[°C] lepkość ma wartość 

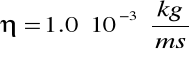
,natomiast dla oleju rycynowego o temp. 20[°C] lepkość wynosi:

Niepewność pomiarowa wynika głównie z niedokładności pomiaru czasu opadania kulki, pomiaru temperatury oraz zanieczyszczenia rurki z olejem.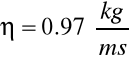

1

---