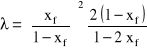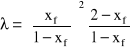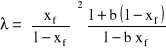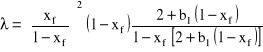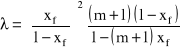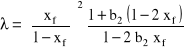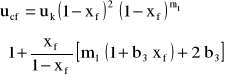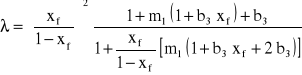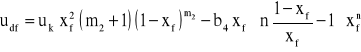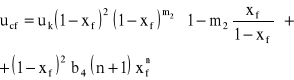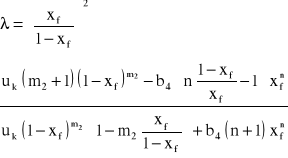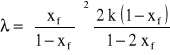Projektowanie kolumn ekstrakcyjnych

Kolumny ekstrakcyjne można podzielić na kolumny pracujące bez użycia energii mechanicznej i kolumny wykorzystujące energię mechaniczną do uzyskania układu kroplowego.

Wśród kolumn z pierwszej grupy wyróżnić można kolumny rozpyłowe (bez zabudowy wewnętrznej), kolumny z wypełnieniem, kolumny półkowe.

W drugiej grupie najbardziej popularne są kolumny z wirującymi dyskami, kolumny pulsacyjne i kolumny z wibrującymi półkami.

Przy projektowaniu kolumn ekstrakcyjnych wykorzystywanych dla określonego układu dwufazowego należy znać równowagę ekstrakcyjną i właściwości obu faz. W trakcie procedury projektowej należy wyznaczyć lub zmierzyć:

1. stopień zatrzymania fazy rozdrobnionej x,

2. maksymalne prędkości faz przy których występuje zjawisko zalewania aparatu, tj. u_cf, u_df,

3. średnią przeciętną wielkość kropel d_vs,

4. pole powierzchni właściwej wymiany masy a.

5. współczynniki wnikania masy po stronie fazy rozdrobnionej β_d i po stronie fazy ciągłej β_c,

Na podstawie tych danych można zaprojektować dwa zasadnicze rozmiary kolumny ekstrakcyjnej, tj. średnicę i wysokość.

Zatrzymanie dynamiczne x jest funkcją zarówno strumienia fazy ciągłej jak i fazy rozdrobnionej, co można zapisać ogólnym równaniem:

.

Jednakże, jeśli rozpatrzyć precyzyjniej tę zależność, to można stwierdzić, że dla małych prędkości fazy ciągłej:

stopień zatrzymania x zależy tylko od strumienia fazy rozdrobnionej:

Podstawą do obliczania obciążeń granicznych jest równanie opisujące prędkość względną obu faz u_R.

lub dla kolumn z wypełnieniem:

Tę prędkość względną Thornton uzależnił także od stopnia zatrzymania i pewnej wielkości nazwanej prędkością charakterystyczną u_k.

(1)

lub dla kolumn z wypełnieniem:

Przez prędkość charakterystyczną u_k należy rozumieć prędkość fazy rozdrobnionej przy u_d→0, oraz u_c→0, czyli prędkość pojedynczej kropli płynącej w aparacie danej konstrukcji w nieruchomej fazie ciągłej.

Oprócz zależności Thorntona w literaturze spotyka się inne postaci zależności prędkości względnej u_R od stopnia zatrzymania i prędkości charakterystycznej:
. Wszystkie wymienione poniżej zależności obowiązują dla przepływu kroplowego. Powstaje pytanie czy faza rozdrobniona płynąca przeciwprądowo przez fazę ciągłą zawsze występuje w postaci kropel. Obserwacje przepływów dwufazowych wykazały, że jeśli faza rozdrobniona płynie przez kolumny wypełnione, to może poruszać się w postaci kropel, może płynąć jako film po wypełnieniu i wreszcie może płynąć w postaci bezkształtnych aglomeratów. Stwierdzono, że krople pojawiają się w kolumnie dla kierunku wymiany masy c→d. Matematycznie można to udowodnić na przykład stosując wymienione poniżej równanie (3).

Przekształćmy równanie do postaci :

Jeśli sporządzić wykres
, to w przypadku gdy punkty doświadczalne ułożą się na prostej można z całą pewnością stwierdzić, że w kolumnie występuje przepływ kroplowy.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

oraz
(9)

Równania te mogą służyć do wyznaczenia granicznych prędkości obu faz, przy których występuje zalewanie kolumny. W tym celu należy obliczyć pochodne i przyrównać je do zera:

i

Dla znanej wartości stosunku strumieni faz, czyli dla znanego stosunku prędkości obu faz:

można obliczyć prędkości faz w punkcie zalewania z równań:

Równanie	Umowne prędkości faz [m^3/(m^2s)]	Stosunek strumieni
1
2
3
4
5
6
7
8
9

Prędkość charakterystyczna u_k zależy nie tylko od właściwości dwufazowego układu ekstrakcyjnego, ale także od konstrukcji aparatu. Prędkość ruchu pojedynczej kropli w nieruchomej fazie ciągłej, poruszającej się w kolumnie bez żadnej zabudowy wewnętrznej można policzyć z zależności Lewicha ze współczynnikiem oporu C_D = 1:

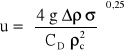
Zatem prędkość charakterystyczną w aparacie o innej konstrukcji można powiązać z prędkością Lewicha prostą proporcją:

,

w której stała C<1 charakteryzuje konstrukcję danego ekstraktora i jest wyznaczana eksperymentalnie.

Do obliczeń prędkości faz w warunkach zalewania w kolumnach z wypełnieniem można wykorzystać empiryczną korelację Kafarowa Dytnierskiego w postaci:

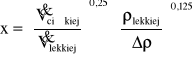
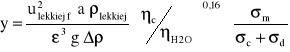
Gdy fazą ciągłą jest faza cięższa c, to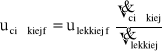

Kolejnym parametrem jest przeciętna średnica kropel występująca w roju poruszającym się przeciwprądowo względem fazy ciągłej. Rozmiar kropel najczęściej definiowany jest jako średnia objętościowo - powierzchniowa średnica zwana średnicą Sautera:

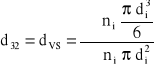
Badania doświadczalne wykazały, że średnica kropel w danym układzie dwufazowym zależy od kierunku wymiany masy, tj. czy substancja ekstrahowana przenika z kropli do fazy ciągłej czy odwrotnie. Stwierdzono także, że zależy od kierunku ruchu kropel, tj. czy poruszają się one w dół czy w górę. Sauterowska średnica kropel zbadana metodą fotograficzną została skorelowana zależnością:

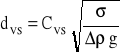
gdzie:

Pole powierzchni właściwej wymiany masy jest związane ze stopniem zatrzymania x i średnicą sauterowską kropel d_VS:

lub dla kolumn z wypełnieniem:

Do opisu wymiany masy konieczna jest znajomość współczynników wnikania masy i w konsekwencji współczynnika przenikania masy. Współczynniki wnikania masy oblicza się z odpowiednich korelacji empirycznych. Korelacje te zostały wyznaczone dla każdego rodzaju konstrukcji zabudowy wewnętrznej i dla przypadków z doprowadzaną z zewnątrz energią mechaniczną lub bez niej.

Jeśli krople poruszają się w kolumnie ulegając kolizjom z elementami zabudowy, to można przyjąć, że po każdej z kolizji następuje całkowite odnowienie powierzchni wymiany masy poprzez doskonałe wymieszanie się wnętrza kropli, czyli tworzą się najlepsze warunki do przyjmowania lub oddawania masy przez kroplę.

Współczynniki wnikania masy w kolumnach z wypełnieniem można obliczyć wykorzystując teorię Higbiego. Zakłada się, pomiędzy dwiema kolejnymi kolizjami upływa czas :

gdzie: l - droga swobodnego ruchu pomiędzy dwoma kolejnymi zderzeniami, m,

- prędkość liniowa kropli, m/s.

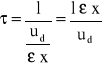
gdzie: u_d - prędkość umowna fazy rozdrobnionej, m³/(m² s).

W kolumnach ekstrakcyjnych, w których dochodzi do częstych kolizji kropel czas swobodnego ruchu kropel jest stosunkowo krótki. Dla takiego przypadku Sherwood i Pigford podają zależność:

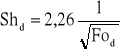
dla Fo_d < 10^-2

Liczby Fouriera i Sherwooda wynoszą odpowiednio:

Po podstawieniu:

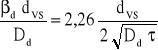
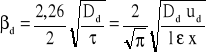
Dla fazy ciągłej obowiązuje wzór Higbiego:

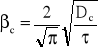
Czas odnawiania powierzchni okreśła się identycznie jak dla fazy rozdrobnionej, bo w czasie zdeżenia kropla odrzuca tak zwany ślad poruszający się wraz z nią, czyli następuje odnowienie się tej porcji fazy ciągłej poruszającej się z kroplą. Zatem:

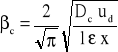
lub wprowadzając liczby bezwymiarowe:

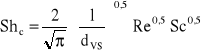
po obliczeniu współczynników wnikania masy można obliczyć współczynnik przenikania masy lub wysokość jednostki przenikania masy. Należy rozróżnić dwa odmienne przypadki. Dla wymiany masy od fazy ciągłej do fazy rozdrobnionej może zachodzić rozdrabnianie fazy wodnej lub rozdrabnianie fazy organicznej.

Dla rozdrabnianej fazy wodnej obowiązują zależności:

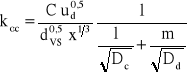
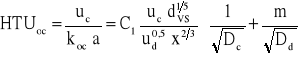
C₁ = 0,22

Dla rozdrabnianej fazy organicznej:

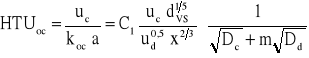
Przenoszenie skali, Analogia Colburna

Wysokość kolumny można zapisać jako iloczyn wysokości jednostki przenikania masy i liczby jednostek przenikania masy:

Wysokości jednostek przenikania masy dla obu faz związane są zależnością:

e oznacza współczynnik ekstrakcji:

Dla linii równowagi przybliżonej prostą:

Jeśli przybliżenie linii równowagi nie przechodzi przez punkt (0, 0), czyli Y=mX+q, to liczbę jednostek przenikania masy wyraża zależność:

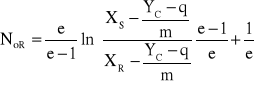
Podczas przenoszenia skali z kolumn laboratoryjnych na kolumny przemysłowe należy pamiętać, że ze względu na różne rozmiary wypełnienia zmieniają się wartości HTU, bo inne są także wartości x i d_VS. Ladha i Degaleesan dla różnych kolumn z wypełnieniami podali zależnośćna obliczanie objętościowego współczynnika przenikania masy liczonego do strony fazy rozdrobnionej:

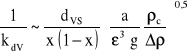
gdzie stosuje się dodatkowe zależności:

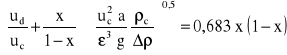
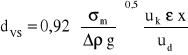
Wielkość kropel w kolumnie laboratoryjnej może różnić się od wielkości kropel w kolumnie przemysłowej nawet więcej niż o 15 %, wówczas:

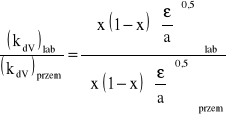
Wiedząc, że:

można napisać:

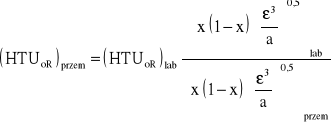
Wówczas dla znanej wysokości kolumny przemysłowej
można obliczyć liczbę jednostek przenikania masy w kolumnie przemysłowej
:

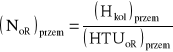
czyli można oszacować wartość stężenia końcowego w rafinacie wypływającym z kolumny przemysłowej na podstawie badań eksperymentalnych wykonanych w mniejszej skali laboratoryjnej:

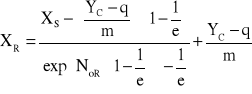
lub można oszacować stopień wyekstrahowania:

EKSTRAKCJA DYSOCJACYJNA

Ekstrakcja dysocjacyjna łączy właściwości ekstrakcji frakcyjnej, ekstrakcji seryjnej (z reekstrakcją) i ekstrakcji z reakcją chemiczną. Jest ona wykorzystywana do rozdziału mieszanin bliskowrzących, lub izomerycznych. Polega ona na wykorzystaniu różnicy stałych dysocjacji substancji poddawanych rozdzielaniu.

Przykładem ekstrakcji dysocjacyjnej może być rozdział m-krezolu (twrz.= 202,4oC) i p-krezolu (twrz.= 202,1oC). Przy różnicy temperatur równej tylko 0,3oC rozdział tych substancji w procesie rektyfikacji jest kosztowny i wymaga sprawnej instalacji. Z tego powodu wykorzystuje się różnice w stałych dysocjacji tych związków. Stała dysocjacji m-krezolu wynosi 9,810-11, a p-krezolu wynosi 6,710-11. Innymi słowy m-krezol jest trochę silniejszym kwasem.

Jeśli mieszanina krezoli zostanie poddana działaniu zasady, to silniejszy kwas (m-krezol) będzie łatwiej reagował z zasadą tworząc sól krezolową, która jest łatwiej rozpuszczalna w fazie wodnej, a praktycznie nierozpuszczalna w fazie organicznej. Słabszy kwas (p-krezol) będzie w większym stopniu pozostawał w formie niezdysocjowanej, która jest rozpuszczalna w fazie organicznej.

Schemat instalacji służącej do rozdziału mieszaniny krezoli przedstawiono na poniższym rysunku. W schemacie tym można dostrzec elementy ekstrakcji frakcyjnej, ekstrakcji z powrotem, oraz ekstrakcji seryjnej (z reekstrakcją).

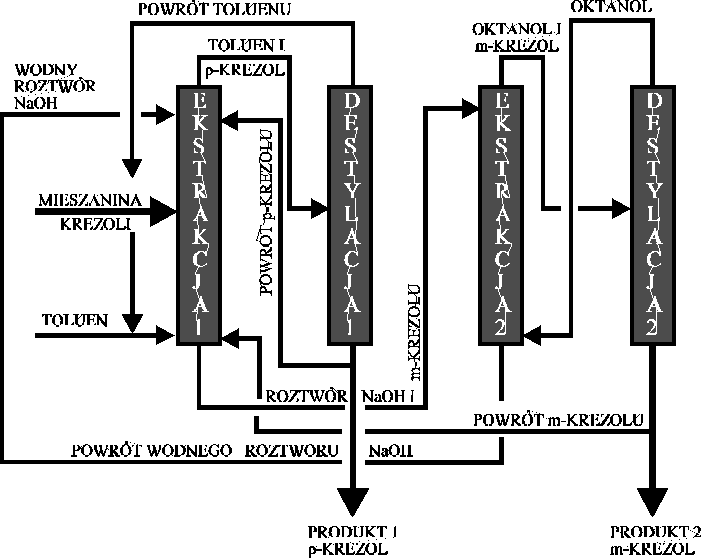
Kolejne etapy procesu rozdzielania mieszaniny meta i para krezolu są następujące:

Ekstraktor 1: Jest to główny aparat ekstrakcyjny, w którym zachodzi początkowy rozdział izomerów krezolu. W aparacie tym zachodzi ekstrakcja frakcyjna, ponieważ surowiec doprowadzany jest do środkowej części aparatu i stosowane są dwa różne rozpuszczalniki. Toluen doprowadzany jest od dołu, a 0,5N wodny roztwór NaOH dopływa od góry kolumny. Krezole zawarte w surowcu rozdzielają się pomiędzy oba rozpuszczalniki.

Toluen nie ma silnego powinowactwa do krezoli, więc początkowo mają one tendencję do przechodzenia do fazy wodnej. Równocześnie ulegają one dysocjacji.
m-krezol ma wyższą stałą dysocjacji, więc łatwiej reaguje z NaOH i jest wiązany
w fazie wodnej w postaci soli. Stężenie m-krezolu w fazie wodnej maleje, a względne stężenie p-krezolu wzrasta. Powoduje to, że m-krezol jest ekstrahowany w większym stopniu z fazy organicznej do fazy wodnej, a p-krezol przechodzi z fazy wodnej do organicznej.

Ekstraktor ten jest bardziej skomplikowany niż prosty aparat do ekstrakcji frakcyjnej, gdyż dopływają do niego dwa dodatkowe strumienie powrotu. Jeden z nich, zawierający p-krezol, wzbogaca szczyt aparatu w ten izomer i powoduje dodatkowy rozdział poprzez wymuszenie dyfuzji m-krezolu do fazy wodnej. Podobnie, w dolnej części kolumny strumień zawierający m-krezol powoduje wzbogacenie fazy wodnej
w ten izomer a tym samym wymusza transport p-krezolu do fazy organicznej. Oba strumienie powrotów poprawiają rozdział izomerów w ekstraktorze.

---