1. Od jakich wielkości zależy siła nośności dowolnego profilu?
P - siła aerodynamiczna (hydrodynamiczna)
Px - opór profilowy
Pz - siła nośna
W przypadku płynów lepkich podczas opływu ciała występuje zawsze opór profilowy Px. Natomiast dla każdego opływanego ciała istnieje takie jego usytuowanie w stosunku do kierunku prędkości woo przy którym nie występuje siła nośna Pz=0
![]()
c - wsp. oporu lub siły nośnej [-]
ρ - gęstość ośrodka w którym się znajduje [kg/m3]
A - umowna powierzchnia odniesienia [m2]
woo - prędkość zredukowana [m/s]
2. Liczba Macha.
Ma < 1 w < Ω - przepływ poddźwiękowy, subsoniczny
Kanał zbieżny Kanał rozbieżny
dA < 0 dA > 0
dp < 0 dp > 0
sprężanie rozprężanie
przyrost pręd. dw > 0 dw < 0 - pręd. maleje
Ma > 1 w > Ω - przepływ naddźwiękowy, supersoniczny
Kanał zbieżny Kanał rozbieżny
dA < 0 dA > 0
dp > 0 dp < 0
sprężanie rozprężanie
dw < 0 - pręd. maleje przyrost pręd. dw > 0
![]()
w - prędkość aktualna
Ω - prędkość dźwięku
![]()
Κ - współ. Izentropy [-]
R - indywidualna stała gazowa [J/kg*K]
T - temp. gazu [K]
Dysza de Lavala (naddźwiękowa)
![]()
Dysza Lavala, urządzenie aerodynamiczne służące do uzyskania przepływu naddźwiękowego, rura o przekroju okrągłym (w dyszach silników) lub prostokatnym (w tunelach aerodynamicznych naddźwiękowych).
W początkowym odcinku dyszy Lavala przekrój podłużny jest zbieżny, następnie rozbieżny. W obszarze zbieżnym na skutek sprężania następuje przyspieszenie przepływu do prędkości dźwięku, dalszy wzrost prędkości przepływu następuje w obszarze rozbieżnym (wykorzystuje się tu zjawisko wzrostu prędkości przepływu ponaddźwiękowego przy rozprężaniu płynu).
3. Pompa strumieniowa.
4. ![]()
Jest to podstawowe równanie maszyn przepływowych (równanie zachowania krętu).
Postać początkowa
![]()
Założenia przy których powstało:
- grubość profilu łopatki równa zeru
- pomijalna lepkość
- stała gęstość
- płyn doskonały
- spełnione równanie ciągłości przepływu
- przepływ ustalony
- pochodna lokalna
![]()
- wektor sił masowych
![]()
Zastosowanie: pompy, turbiny, sprężarki.
m - strumień masy [kg/s]
r1,r2 - promienie (wew. i zew.) [m]
wU1,wU2 - prędkości unoszenia [m/s]
5. Kawitacja.
w1=0, w2=w
pz=ps - ciśnienie w pompie
![]()
![]()
ps>pw - kawitacja!
Kawitacja jest to zjawisko spowodowane lokalnym spadkiem ciśnienia cieczy poniżej ciśnienia wrzenia w określonej temp. (powst. pęcherzyki pary). Ciecz podczas skraplania uderza o metal, w połączeniu z korozją powstają głębokie wżery w metalu. Podczas kawitacji powstają efekty akustyczne oraz drgania przewodu. Kawitacja powoduje uszkodzenie elementów metalowych znajdujących się w obszarze obniżonego ciśnienia. Najbardziej narażone są wyloty pomp wirnikowych. Aby zapobiec kawitacji w pompach należy dobierać wysokość ssania tak, aby warunek ps>pw (ciśnienie ssania było większe od ciśnienia wrzenia) zawsze był spełniony z pewnym zapasem.
6. Ogólny wzór na prędkość opadania cząstki kulistej.
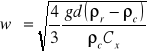
ρr - gęstość cząstki (fazy rozproszonej)
ρc - gęstość płynu (fazy ciągłej)
d - średnica cząstki kulistej
g - przysp. ziemskie [m/s2]
Cx - WSP. oporu [-]
7. Prędkość opadania cząstki w zakresie laminarnym.
![]()
![]()
- wsp. lepkości dynamicznej płynu [kg/m*s]
8. Prędkość opadania cząstki w zakresie turbulentnym.
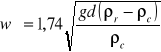
9. Prędkość sedymentacji.
Prędkość sedymentacji ws jest prędkością opadania względem nieruchomych ścian naczynia.
ws = wr - wc wr = 7
10. Efekt Magnusa.
W skutek cyrkulacji następuje rozrzedzenie linii prądu na dole a zagęszczenie na górze, wobec czego na dolną powierzchnię kuli działa większe ciśnienie niż na jej górną powierzchnię, co daje w wyniku siłę nośną. Działanie siły nośnej w przypadku wirujących ciał nosi nazwę efektu Magnusa.
11. Cyrkulacja prędkości.

Jest to całka liniowa z iloczynu skalarnego prędkości w i elementu tej krzywej ds.
12. Nieustalony przepływ wody w przewodzie (uderzenie hydrauliczne).
![]()
- okres uderzenia (czas)
f.n. - faza nadciśnienia (zagęszczeniowa)
f.p. - faza podciśnieniowa (rozrzedzeniowa)
Uderzenie hydrauliczne występuje, gdy płynąca woda zostaje nagle zatrzymana np. zamknięcie zaworu, zatrzymania pompy. Ek wody zanika i wywołuje gwałtowny wzrost ciśnienia o wartości ∆p (jest to uderzenie dodatnie). Po nagłym zamknięciu zaworu , gdzie tz=0 i przyjęciu braku ściśliwości wody i braku sprężystości ścian rury, ciśnienie powinno wzrosnąć do poo W rzeczywistości tz>0 a woda jest ściśliwa i rura sprężysta, to ciśnienie wody wzrasta o ∆p. Przyrost ∆p w postaci fali ciśnieniowej odbija się od zaworu i przechodzi do zbiornika - jest to fala gaszeniowa. Natomiast fala rozrzedzeniowa pojawia się po odbiciu od wody w zbiorniku.
13. Rzeczywisty przebieg zmian ciśnienia przy zaworze.
Charakter zachowania się wody po zamknięciu zaworu. Pomiar ciśnienia przyrządem wykazuje, że amplituda ruchu falowego wskutek tłumienia nie jest jednakowa.
14. Jak oblicza się straty ciśnienia przy przepływie płynu przez różne instalacje?
Jest to suma strat tarcia oraz oporów miejscowych.
pstr= pstr t + Σpstr m
Straty ciśnienia wskutek tarcia można obliczyć ze wzoru Darcy'ego-Weisbacha:
![]()
λ - wsp. oporów liniowych [-]
L - dł. przewodu [m]
D - średnica przewodu [m]
ρ - gęstość cieczy [kg/m3]
w - prędkość [m/s]
Wzór ten dotyczy przepływu laminarnego i turbulentnego przy czym zmienia się λ:
Laminarny - λ = 64 / Re
Turbulentny - λ = 0,3164 / 4√Re
Straty ciśnienia w skutek oporów miejscowych. Opory te wywołane są przeszkodami jak: kolana, przewężenia, rozgałęzienia itp. Oblicza się je z ogólnego wzoru:
![]()
![]()
- wsp. straty miejscowej
15. Przepływ laminarny w przewodzie płaskim.
![]()
Równanie to opisuje rozkład prędkości w przewodzie płaskim - przepływ Poisenille'a.
Prędkość max jest w środku przewodu ![]()
i równa się
![]()
natomiast średnia prędkość
![]()
16. Założenia do przepływu dwuwymiarowego.
Wy=0
Fmy=0
![]()
wz=0 - prędkość jest równoległa do osi x
wx=w - jeden kierunek prędkości
![]()
- przepływ ustalony
![]()
- prędkość wx nie zmienia się po x
Fmx1= Fm2=0 - pomijamy siły masowe
17. Przepływ laminarny w przewodzie o przekroju kołowym.
Jest to układ rozpatrywany osiowo-symetrycznie, nazywa się przepływem Hagena-Poisenille'a. Równanie opisujące rozkład prędkości wygląda:
![]()
Maksymalna prędkość jest w osi przewodu dla r=0
![]()
![]()
18. Przepływ turbulentny.
Rozkład prędkości opisuje wzór potęgowy Prandtla (z badań empirycznych):

1/n = 1/6 - 1/10 wykładnik potęgowy dla liczb Reynoldsa odnoszący się dla ścian gładkich.
1/n = 1/4 - 1/5 dla ścian chropowatych
![]()
19. Warstwa przyścienna lam. i turb.
I - utrata stateczności warstwy laminarnej
II - warstwa laminarna
III - warstwa turbulentna
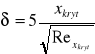
![]()
Przejście warstwy laminarnej w turbulentną następuje w wyniku utraty stateczności przepływu w warstwie laminarnej. Obliczenia warstwy turbulentnej są bardzo złożone.
20. Zmiana pędu w przepływie jednowymiarowym.
![]()
Równanie to nosi nazwę reakcji płynu, jest to siła z jaką płyn działa na ścianę przewodu. Równanie to można wykorzystać do obliczania sił działających na opływane ciało.
21. Rozkład ciśnień w cieczy.
p = pc + ρgz - jest to równanie manometryczne, które pozwala obliczyć ciśnienie na dowolnej odległości z. Szukane ciśnienie jest sumą ciśnienia otoczenia i ciśnienia hydrostatycznego, które wynosi pn = ρgz
22. Nadciśnienie i podciśnienie.
Ciśnienie mierzymy względem ciśnienia atmosferycznego i mówi się o nim jako nadciśnienie, natomiast ciśnienie mniejsze od ciśnienia atmosferycznego nazywa się podciśnieniem.
po = 760 mmHg = 1bar = 0,1 MPa
23. Parcie cieczy na płaskie powierzchnie ścian.
dF = pn Da
pn = ρgz
![]()
![]()
![]()
F = ρgzsA
Zs - wsp. środka ciężkości [m]
Zn - wsp. środka parcia [m]
Parcie zależy od kąta α, gdyż ze zmianą kąta α zmienia się głębokość środka ciężkości.
24. Paradoks hydrostatyczny.
Parcie jest równe ciężarowi słupa cieczy o podstawie A i wysokości z. Zjawisko to nazywa się paradoksem hydrostatycznym.
F = pn A = gza = ρgV = mg = G
25. Parcie cieczy na zakrzywione powierzchnie cieczy.
S - środek ciężkości Ax
N - środek parcia Ax
So - środek ciężkości słupa cieczy nad powierzchnią zakrzywioną
No - środek parcia F
![]()
Fx = ρgzsAx
![]()
26. Wypór hydrostatyczny.
A = A1 + A2
Fx = Fx
Fz = Fz1 + Fz2
Parcie w kierunku osi x jest zerowe, ponieważ dwa przeciwnie skierowane różne parcia Fx dotyczą tej samej powierzchni. Parcie w kierunku osi z jest różnicą parcia Fz1 i Fz2 Wypadkowe parcia działające do góry na zanurzone ciało nazywa się wyporem. Wypór cieczy wynosi. Równanie to opisuje prawo Archimedesa:
Fz = W = G = ρgV
G, V - objętość wypartej cieczy przez zanurzone ciało.
27. Pływanie ciał.
w=w*
G=W
Gl=Wl
M - metacentrum
M - wysokość metacentryczna
Mamy 3 przypadki:
1) G<W ciało zostaje wyparte do góry i częściowo się wynurza. Ciało zacznie pływać gdy ciężar ciała będzie równy wyporwi zanurzonej części ciała.
2) G=W ciało jest zanurzone na dowolnej głębokości
3) G>W ciało tonie.
Metacentrum jest to punkt przecięcia linii działania wyporu chwilowego W* i pionowej osi ciała pływającego. Odległość od punktu M do środka ciężkości ciała S nazywa się odległością metacentryczną.
28. Równowaga względna cieczy.
1) dU=0 dp=0
dU=Xdx + Ydy + Zdz
X=-a Y=0 Z=-g
ρdU=0
ρ(Xdx + Ydy + Zdz)=0
ρ(-adx - gdz)=0
![]()
ax + gz = C
z=zo to x=0
C=gzo ax + gz = gzo
![]()
2) X=rw2 Y=0 Z=-g
To samo
ρ(rw2dr - gdz)=0
![]()
![]()
r=0 z=zo
C= -gzo
![]()
![]()
Z równań:
ρ(-adx - gdz)=0 oraz ρ(rw2dr - gdz)=0 można obliczyć ciśnienie w dowolnym punkcie cieczy oraz po podstawieniu za dp=0 można otrzymać powierzchnie ekwipotencjalne.
29. Powierzchnie ekwipotencjalne.
dp=ρdU dla dp=0 dU=0 oznacza to, że powierzchnie jednakowego ciśnienia p=const (pow. izobaryczne) są w polu sił masowych jednocześnie powierzchniami stałego potencjału U=const, czyli powierzchniami ekwipotnecjalmymi.
Własności: gęstość i ciśnienie cieczy nie zmienia się wzdłuż pow. ekw., pow. swobodna jest pow. ekw., pow. rozdziału linii cieczy o różnych gęstościach nie mieszających się ze sobą jest pow. ekw.
Kształt pow. ekw. zależy od:
30. Wypływ cieczy przez mały otwór o dowolnym kształcie i zaokrąglonych krawędziach.
W1=0 bo A1>>A2
![]()
w1A1= w2A2
![]()



gdy A2<<A1 to A2 / A1=0
Korzysta się wtedy ze wzoru Torricellego:
![]()
31. Wypływ cieczy przez duży otwór o przekroju prostokątnym axb i zaokrąglonych krawędziach.
W1=0 A1>>A2 analogicznie jak u góry
![]()
32. Wypływ cieczy z otworu zaokrąglonego i ostrokrawędziowego.
![]()
α - wsp. wypływu
φ - wsp. uwzględniający lepkość (straty prędkości)
ψ - wsp. przewężenia strugi
![]()
A2p - powierzchnia przekroju strugi
A2 - pow. otworu
![]()
w2 - prędkość rzeczywista
w2t - prędkość teoretyczna
33. Czas wypływu przez mały otwór ostrokrawędziowy.

34. Rozkład ciśnień na ścianach wolnostojącego budynku.
0<l1<1 0<l2<1
nadciśnienie:
![]()
podciśnienie:
![]()
Powietrze zderzające się z czołową ścianą budynku traci na prędkości i zmienia kierunek, a ciśnienie statyczne wynosi
![]()
Następnie ciśnienie całkowite nieznacznie maleje na skutek strat energii, a ciśnienie dynamiczne znacznie rośnie, lecz ciśnienie statyczne spada poniżej ciśnienia atmosferycznego. Na tylnej ścianie budynku panuje mniejsze ciśnienie od ciśnienia atmosferycznego, a za budynkiem powstaje obszar zawirowań. Ciśnienie to wynosi
![]()
C2 - wsp. określający jaka część ciśnienia statycznego zmieniła się w ciśnienie dynamiczne.
C1 - wsp. określający jaka część ciśnienia dynamicznego zmieniała się w ciśnienie statyczne.
Ciśnienie statyczne działające na ściany budynku wyrażone jest jako nadciśnienie p+ lub podciśnienie p-.
35. Twierdzenie Gaussa-Ostrogrodzkiego.
![]()
![]()
dA - pow. elementarna [m2]
p - ciśnienie [Pa]
![]()
- rozkład ciśnienia na x [N/m2]
36. Równanie równowagi płynu w postaci wektorowej.
![]()
Wykorzystujemy tw. Gausa-Ostrogradzkiego:
![]()
Po podstawieniu
![]()
![]()
po scałkowaniu otrzymujemy:
![]()
grad p - rozkład ciśnienia na kierunki [Pa]
dA - powierzchnia elementarna [m2]
dV - związek z objętością [m3]
Fm - jednostkowa siła masowa [m/s2]
Ρ - gęstość [kg/m3]
37. Równanie równowagi w postaci skalarnej.
![]()
![]()
Równanie to przedstawiamy w postaci 3 równań skalarnych:
![]()
dla y i z tak samo.
Dodajemy stronami:
![]()
Otrzymujemy:
![]()
38. Równanie równowagi w potencjalnym polu sił masowych.
Pochodne cząstkowe są składowymi jednostkowej siły masowej:
![]()
dla y i z tak samo.
![]()
![]()
39. Co oznacza funkcja dysypacji energii.
Fun. Rozpraszania energii rozumiana jako ciepło, są to opory przepływu (zw. z naprężeniami statycznymi) związane z tarciem wew.
![]()
- ciepło tarcia
Dyssypacja Onegi mech. to część pracy sił powierzchniowych, która nie ulega przekształceniu w e. kinetyczną płynu lecz w e. wew. płynu (podnosząc jego temp.).
40. ![]()
Jest to równanie ciągłości przepływu. Ogólna postać tego równania jest:
![]()
Przyjmujemy kostkę jako model geometryczny płynu
Ścianka I: ![]()
Ścianka II: 
Po odpowiednich działaniach:
![]()
Wykorzystując definicję wektora prędkości otrzymujemy:
![]()
Q - strumień masy [kg/s]
![]()
- zmiana prędkości po czasie
Zastosowanie: szczególne formy równania ciągłości są stosowane z reguły w hydraulice dla jednowymiarowych przepływów (jako założenie upraszczające).
41. ![]()
Jest to równanie energii. Ogólna postać to:
![]()
Q - ciepło
U - en. wew.
EF - en. przeciw siłom powierzch.
![]()
1 - związek z przewodzeniem
Każda energia jest zależna od składowych czasu. E=E(z,y,z,t)
![]()
![]()
Analogicznie na pozostałe kierunki.
Z prawa Furie:
![]()
λ=idem λ= λ(T) idem

Zatem: ![]()
Q - energia [W]
T - temp. [K]
Λ - wsp. przewodzenia ciepła [W/m*K]
▼ - nabla (operator) [-]
42. ![]()
Jest to postać równania Naviera-Stokesa. Wynika ono z równania Naviera-Stokesa (równanie ruchu cieczy lepkiej)
![]()

Założenia przy jakich powstało:
w2=0 - przepływ w kierunku x
wx2w - jeden kierunek prędkości
![]()
- przepływ ustalony
![]()
- prędkość wx nie zmienia się po x
Fm1 = Fm2 = 0 - pominięte siły masowe
![]()
- brak zmian ciśnienia na kierunku z
![]()
- ukł. Płaski
![]()
- zmiana ciśnienia na kier. X
ρ - gęstość [kg/m3]
μ - wsp. dynamiczny [N*s/m2]
ν - wsp. kinematyczny [m2/s]
▼2 - operator Laplace'a [-]
w - wektor prędkości [m/s]
43. ![]()
wynika z równania EULERA {ruchu płynu,wirowy}
załozenia:
![]()
ruch jest ustalony
δ=idem płyn nieścisliwy
otrzymujemy równanie: ![]()
korzystam z równań:
grad u=Fm -![]()
u=gz -![]()
44. Postacie równania Bernoulliego.

45. Korzyści z liczb kryterialnych.
Liczby kryterialne:wynikaja z twiedzen teoripodobienstwa , pozwalaja na stworzenie i badanie modeli rzeczywistych obiektow. Spełniajac warunki teorii podobienstwa (3 litery kryterialne) można poznac rzeczywwiste wielkosci charakteryzujace obiekt na podstawie wykonanego modelu. Sa bezwymiarowe i uniwersalne:
Jeżeli :![]()
- stały stosunek
Np.:
![]()
![]()
![]()
Jeśli kiedys będę dokonywał badań i będę miał równania opisujące model,to możemy przejsc na model rzeczywisty. Należy bowiem uwzglednic liczby Reynoldsa,Eulera,Freuda
46. ![]()
Jest to równanie Reynoldsa (reakcja płynu między czopem a panwią). Dzięki niemu można uzyskać rozkład ciśnień. Pochodzi od równania Naviera-Stokesa:
![]()
W warunkach wx=wx(x,y), wz(x,y), p=p(x,y)
Warunki: przepływ ustalony, stała gęstość, prędkość na kierunek y=0
47. Wektorowa postać równania Naviera-Stokesa.
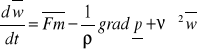
Fm-siły masowe na kierunkach x,y,z,
![]()
-zmiany predkosci w czasie na x,y,z
1/ρ grad p-od sil powierzchniowych na x,y,z
![]()
-od zmian predkosci a kierunkach x,y,z
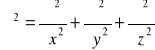
1 - siły bezwładnościowe
2 - siły czynne masowe
3 - siły ciśnieniowe
4 - siły lepkości
Wyszukiwarka
Podobne podstrony:
fizyka-egzam, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
Energia relatywistyczna, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
elektrycznosć i magnetyzm nr 13, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
zagadnienia z fizyki na egzamin-1, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
zagadnienia z fizyki na egzamin, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
kinematyka i dynamika statyczna, STUDIA, Polibuda - semestr I, Fizyka, zaliczenie
217, STUDIA, Polibuda - semestr I, Fizyka, laborki, 217
Mechanika-2011, Polibuda, I semestr, fizyka
Fala to zaburzenie, STUDIA, Polibuda - semestr I, Fizyka, laborki, 217
215--, STUDIA, Polibuda - semestr I, Fizyka, laborki, 215
tresyta, STUDIA, Polibuda - semestr I, Fizyka
217 - instrukcje, STUDIA, Polibuda - semestr I, Fizyka, laborki, 217
sciśliwość gruntu, STUDIA, Polibuda - semestr III, Mechanika gruntów, Sprawozdania
Mechanika ogólna2, STUDIA, Polibuda - semestr I, Mechanika ogólna
PYTANIA skoczek, STUDIA, Polibuda - semestr IV, Organizacja Produkcji Budowlanej, obp zaliczenie
więcej podobnych podstron