POLITECHNIKA ŚLĄSKA

WYDZIAŁ ELEKTRYCZNY

semestr II, grupa T2

Wyznaczanie energii maksymalnej promieni β metodą absorpcyjną.

Sekcja 3:

Janulek Jarosław

Blechinger Sebastian

1.WPROWADZENIE TEORETYCZNE

Rozpad beta polega na przemianie jednego neutronu w jądrze atomu w proton, której towarzyszy emisja promieniowania β ( czyli elektronu naładowanego ujemnie e^- lub dodatnio e⁺) i odpowiednio antyneutrina (ν) lub neutrina (υ). Równanie tej przemiany zapisujemy symbolicznie w postaci:

lub
, gdzie X i Y oznaczają umowne symbole chemiczne pierwiastka, którego jądro ulega rozpadowi oraz pierwiastka, którego jądro powstało w wyniku danej przemiany jądrowej, Z - liczbę atomów ( czyli liczbę porządkową pierwiastka chemicznego w układzie okresowym pierwiastków, równą liczbie protonów w jądrze atomowym a tym samym liczbie elektronów obojętnego atomu danego pierwiastka), A - liczbę masową , czyli liczbę nukleonów ( protonów i neutronów ) w jądrze atomowym danego izotopu pierwiastka .

Widmo energetyczne elektronów w czasie rozpadu promieniotwórczego β jest widmem ciągłym, o ściśle określonej energii maksymalnej (E_max). Kształt widma odzwierciedla fakt różnego możliwego podziału energii rozpadu pomiędzy elektron i antyneutrino ( neutrino ). Maksymalna energia widma odpowiada sytuacji, gdy elektron unosi całą dostępną energię równa energii przejścia β. Energie elektronów promieniowania β obejmują szeroki zakres wartości - od energii rzędu 10⁴[eV] do 10⁶[eV] dla różnych izotopów promieniotwórczych. Ponieważ masa elektronów jest mała , ich energia spoczynkowa wynosi zaledwie 0,51 [MeV]. Wynika stąd, że już elektrony o energii 10⁴[eV] muszą być opisywane za pomocą wzorów mechaniki relatywistycznej. Elektrony β wiązki przechodzącej przez warstwę jakiegoś ciała doznają zderzeń z napotkanymi po drodze atomami.

Zderzenia te mogą być sprężyste bądź niesprężyste, a więc połączone ze stratami energii na wzbudzenie lub jonizację atomów. W przypadku elektronów o niezbyt wielkich energiach największą rolę odgrywają straty ich energii wskutek jonizacji atomów ośrodka, przez który przechodzi. Strata energii ( w zderzeniach niesprężystych ) na jednostkę drogi ( zwana zdolnością hamującą ośrodka ) dla cząstki o ładunku Ze i przelatującej z prędkością v przez substancję, której atomy mają po Z' elektronów, jest określona wzorem Bethego:

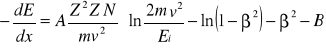
, gdzie:

m. - masa elektronu, E_i - średnia energia jonizacji atomów danego ośrodka, b=ν/c, c - prędkość światła w próżni, ν - prędkość cząstki.

, gdzie: e - ładunek elektronu,ε_o - przenikalność dielektryczna próżni, B - stała.

Zdolność hamująca ośrodka jest tym większa, im większa jest jego liczba atomowa. Z'. Natomiast dla danego ośrodka straty energii cząstki na jednostkę drogi są tym większe, im większy jest jej ładunek Ze oraz im mniejsza jest prędkość ν. Dla elektronu przy ustalonej jego energii początkowej istnieje pewna długość drogi po przebyciu której traci on całą swoją energię i wówczas może być wychwycony przez atom. Grubość absorbenta, przez który żaden elektron o danej energii nie może przejść, nazywamy zasięgiem promieniowania β. Jeżeli elektrony padające na absorbent posiadają różne energie, wówczas używa się pojęcia maksymalnego zasięgu x_max, który odpowiada zasięgowi elektronów o największej energii E_max. Gdy rozpatrujemy zależność ilości elektronów od drogi x, jaką przebyły w danej substancji , to przy wartościach x<0,8x_max z wystarczająco dobrym przybliżeniem możemy stosować wzór: N=Noexp(-μx), gdzie μ oznacza tzw. liniowy współczynnik pochłaniania. Wzór powyższy możemy oczywiście zapisane także w postaci:

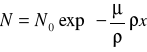
, gdzie

μ/ρ [cm²/g] nazywamy masowym współczynnikiem pochłaniania elektronów. Wielkość ρx oznacza masę na jednostkę powierzchni danej substancji ([g/cm²])

2.PRZEBIEG ĆWICZENIA

1.Włączamy przelicznik.

2.Mierzymy tło licznika (pomiar liczby zliczeń w czasie 10 min. przy nieobecności preparatu).

3.Preparat promieniotwórczy umieszczamy w domku ołowianym w odległości ok. 1cm od okienka licznika.

4.Nastawiamy tryb pomiaru czasu zliczania [s] zadanej liczby impulsów, np. 10⁴.

5.Pomiary wykonujemy najpierw bez absorbenta, a następnie z płytkami aluminiowymi dokładanymi na stos na preparacie.

6.Rysujemy wykres zależności N'=f(d).

7.Na papierze półlogarytmicznym wykreślamy zależność N'=f(d). Przedłużamy wykres do przecięcia się z rzędną N_t. Określamy zasięg liniowy promieni β w aluminium.

8.Obliczamy zasięg masowy promieni β. Na podstawie danych poniższej tabeli rysujemy wykres zależności zasięgu masowego promieni β w aluminium od ich energii maksymalnej.

Emax [keV]	100	150	200	250	300	400	500	800	1000
Zm[mg/cm^2]	13,5	26,5	42	59	78	120	165	310	420

9.Określamy energię maksymalna promieni β stosowanego preparatu ²⁰⁴Tl.

10.Przeprowadzamy graficzną analizę błędów.

3.TABELE POMIAROWE

Lp.	Grubość d [mm]10^-3	Impulsy N	Czas t [s]	N' [1/min]	lnN'
1	0	10^4	19,58	30644±175	10,33
2	20	10^4	21,61	27765±167	10,23
3	40	10^4	23,37	25674±160	10,15
4	60	10^4	27,62	21723±147	9,99
5	80	10^4	29,55	20305±142	9,92
6	95	10^4	30,59	19614±140	9,88
7	115	10^4	32,80	18293±135	9,81
8	135	10^4	35,72	16797±130	9,73
9	155	10^4	37,90	15831±126	9,67
10	175	10^4	40,19	14929±122	9,61
11	195	10^4	42,92	13979±118	9,55
12	210	10^4	45,11	13301±115	9,49
13	230	10^4	48,76	12305±111	9,42
14	250	10^4	57,66	10406±102	9,25
15	270	10^4	62,67	9574±98	9,17
16	290	10^4	67,35	8909±94	9,09
17	310	10^4	71,18	8429±92	9,04
18	330	10^4	75,20	7979±89	8,98
19	350	10^4	82,80	7246±85	8,89
20	370	10^4	89,69	6690±82	8,81
21	390	10^4	96,57	6213±79	8,73
22	760	10^3	265,2	226±15	5,42
23	2620	10^2	151	40±6	3,68

Z pierwszego pomiaru - liczby zliczeń w czasie 10 min. przy nieobecności preparatu - otrzymaliśmy tło licznika, które wyniosło:

N_t=164, N_t=16,4/min

Błąd obliczenia tła otrzymujemy ze wzoru:

ΔN_t=4

Ostatecznie mamy: N_t=16,4±4.

Gęstość aluminium

Następnie aby obliczyć zasięg masowy narysowaliśmy wykres zależności: ln(N')=f(d).

Otrzymaliśmy prostą o równaniu:

ln(N')=(a±Δa)⋅(b±Δb)

ln(N')=(-0.00267±0.00024)⋅d+(9.95±0.15)

Z powyższego równania wyliczono zasięg liniowy wstawiając wartość tła licznika ln(N_t).

Otrzymano następujący wynik:

Z_l=1.82±0.22 [mm]

Mnożąc zasięg liniowy przez gęstość aluminium 2.7 [g/cm²] otrzymujemy zasięg masowy:

Z_m.=491±59 [mg/cm²]

Następnie sporządzamy wykres zależności energii maksymalnej od zasięgu masowego.

Zauważamy, że zależność energii maksymalnej od zasięgu cząstek β jest zależnością liniową opisaną przez prostą:

E_max=(a±Δa)⋅Z_m.+(b±Δb)

E_max=(2.183±0.067)⋅Z_m.+(112±13)

Wstawiając otrzymane wartości zasięgu masowego do powyższego równania otrzymujemy wartość energii maksymalnej oraz błąd:

E_max=1183±129 [keV]

4.WNIOSKI I UWAGI

Na podstawie dokonanych pomiarów wykonano wykresy zależności zmierzonych impulsów na minutę N' w zależności od grubości absorbenta , którym były płytki aluminiowe , oraz zależności

zasięgu masowego promieni
w aluminium od ich energii maksymalnej. Po określeniu z wykresu ln(N')=f(d) zasięgu liniowego promieni
obliczono zasięg masowy przyjmując gęstość aluminium
. Nanosząc tak obliczony zasięg masowy „Z” promieni
na wykres E_max=f(Z_m.)

odczytano z wykresu zakres energii . Odczytana energia E_m.=1183±129[keV] .

Wg tabeli określającej Emax dla wybranych izotopów , Emax dla :

wynosi 1.8 MeV

wynosi 1,47 MeV

wynosi 0,8 MeV

W naszym przypadku badaną próbką był izotop
.

Różnica między energią odczytaną z tabeli , a energią wyznaczoną doświadczalnie wynika zarówno z dokładności pomiarów jak również z dokładności odczytu z wykresów . Zaznaczono w kilku punktach słupki błędów od wielkości N' oraz poprowadzono proste regresji oraz proste określające obszar błędu zliczeń tła . Na tej podstawie wyznaczono zasięg cząstek
w aluminium:

Z_l=1.82±0.22[mm]

---