Wydział	Dzień/godz. Czwartek 8.00 - 12.00		Nr zespołu
Inżynierii Środowiska	Data ćwiczenia (sem. letni/zimowy) 08.10.2009		3
Nazwisko i Imię	Data oddania sprawozdania:		Ocena
1. Pająk Bartłomiej
2. Wiechetek Mateusz
3. Nowak Katarzyna 4. Korkuć Maciej
Temat ćwiczeń: Pomiar nadciśnienia statycznego		Podpis prowadzącego:

Cel i zakres ćwiczenia

Cel:

• Zbadanie wpływu położenia manometru mechanicznego na wartość pomiaru

• Analiza błędów z uwzględnieniem zakresu mierniczego i klasy urządzenia oraz określenie średniej wartości małej liczby pomiarów za pomocą testu t-Studenta

• Poznanie metod wykonywania pomiarów ciśnienia statycznego oraz zasad działania używanych w tym celu manometrów cieczowych i mechanicznych.

Zakres:

• Pomiary nadciśnienia w przewodzie za pomocą manometrów - cieczowego M1 oraz mechanicznych M2, M3, M4 (dla manometru M4 kilka różnych wariantów wzniesienia względem osi przewodu)

• Wyznaczenie wartości średniej nadciśnienia z małej liczby pomiarów za pomocą narzędzi statystycznych (test t-Studenta)

• Określenie wpływu zakresu mierniczego i klasy urządzenia na błędy pomiarowe

• Wyznaczenie gęstości cieczy manometrycznej

Przebieg ćwiczenia

Początek naszego doświadczenia stanowiło sprawdzenie układu pod względem technicznym a skupiliśmy się na upewnieniu, że wszystkie zawory są zamknięte. Następnie wypełniliśmy hydrofor wodą i sprawdziliśmy, czy nadciśnienie w nim nie przekracza wartości maksymalnej (domyślnie 1,5 bar). Kolejną czynnością było odcięcie zasilania wewnętrznego i otwarcie zaworu na doprowadzeniu z hydroforu (P<0,5 bar). Potem z kolei odpowietrzyliśmy manometry i napełniliśmy przewód wodą. Następnie wykonaliśmy serie pomiarów na układzie składającym się ze stalowego przewodu zasilanego z sieci wodociągowej poprzez zbiornik hydroforowy. Kończąc opróżniliśmy przewód i hydrofor z wody.

Seria pomiarowa	Manometr	Jednostka	Odczyt		a [cm]	Odczyt w Pa
1	M1	[mm sł. c. m.]	H1 =	508	---	----
								H2 =	-523
								ΔH =	1031
				M2			[MPa]	---	0,13	18	130000
								---
				M3			[kg/cm^2]	---		1,36	23	133416
								---
				M4	[bar]	pn1 =	1,32	0	132000
						pn2 =	1,3	20	130000
						pn3 =	1,28	40	128000
			pn4 =	1,27	60	127000
			pn5=	1,25	80	125000

Wraz ze wzrostem wysokości, spada mierzone ciśnienie na manometrze 4, a wynika to ze wzoru :

p =
gdzie
i g są stałymi.

1. druga seria pomiarowa dla ciśnienia w hydroforze 1,2kg/cm²:

Seria pomiarowa	Manometr	Jednostka	Odczyt		Odczyt [Pa]	a[cm]
			2	M1			[mm sł. c. m.]	H1 =	460		---
								H2 =	-473
								ΔH =	933
				M2			[MPa]	---	0,12	120000	18
								---
				M3			[[kg/cm^2]	---		1,25	122625	23
								---
		M4	[bar]	pn5 =	1,12	112000	80

2. trzecia seria pomiarowa dla ciśnienia w hydroforze 1,05kg/cm²:

Seria pomiarowa	Manometr	Jednostka	Odczyt		Odczyt [Pa]	a[cm]
			3	M1			[mm sł. c. m.]	H1 =	398		---
								H2 =	-410
								ΔH =	808
				M2			[MPa]	---	0,105	105000	18
								---
				M3			[kg/cm^2]	---		1,1	107910	23
								---
		M4	[bar]	pn5 =	0,9	90000	80

c) czwarta seria pomiarowa dla ciśnienia w hydroforze 0,9kg/cm²:

Seria pomiarowa	Manometr	Jednostka	Odczyt		odczyt [Pa]	a[cm]
			4	M1			[mm sł. c. m.]	H1 =	340		---
								H2 =	-350
								ΔH =	690
				M2			[MPa]	---	0,09	90000	18
								---
				M3			[kg/cm^2]	---		0,95	93195	23
								---
		M4	[bar]	pn5 =	0,83	83000	80

Oznaczenia zastosowane w tabelach:

c.m. - ciecz manometryczna

a - wysokość osi manometrów (M2, M3, M4) nad osią przewodu [cm]

H₁ - odczyt lewego ramienia manometru cieczowego (M1) [mm sł. c.m.]

H₂ - odczyt prawego ramienia manometru cieczowego (M1) [mm sł. c.m.]

ΔH - wskazanie manometru cieczowego M1 [mm sł. c.m.]

• [kg/cm²] na [MPa] (dla manometru M3):

W tym wypadku skorzystaliśmy z zależności:

98066,5 Pa = 1 kg/cm²

Na zasadzie proporcji obliczyliśmy potrzebne nam ciśnienia w żądanej jednostce.

• [bar] na [MPa] dla manometru M4):

Przy tej zamianie również skorzystaliśmy z znanej nam zależności:

1 bar = 0,1 MPa

Zatem gęstość cieczy manometrycznej liczymy ze wzoru :

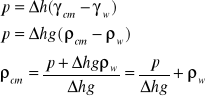
Gdzie :

ciężar właściwy cieczy manometrycznej

ciężar właściwy w naszym przypadku wody

gęstość wody

gęstość cieczy manometrycznej

różnica wskazań manometru

Zatem dla równego poziomu manometrów otrzymujemy wyniki

Seria pomiarów	Manometr 2 [Pa]	Manometr 3 [Pa]	Manometr 4 [Pa]
1	130000+1763=131763	133416+2253=135669	125000 +7835=132835
2	120000+1763=121763	122625+2253=124878	112000+7835=119835
3	105000+1763=106763	107910+2253=110163	90000+7835=97835
4	90000+1763=91763	93195+2253=95448	83000+7835=90835

Seria pomiarów	M2 [MPa]	M3 [MPa]	M4 [MPa]
1	0,1318	0,1357	0,1328
2	0,1218	0,1249	0,1198
3	0,1068	0,1102	0,0978
4	0.0918	0,0954	0,0908

tak wiec możemy policzyć gęstość cieczy manometrycznej

Seria pomiarów	Gęstość M2 [kg/m^3]	Gęstość M3 [kg/m^3]	Gęstość M4 [kg/m^3]
1	14029,7	14415,3	14128,6
2	14305,9	14644,6	14087,4
3	14472,2	14901,2	13336,8
4	14560,4	15092,3	14412,7

Zatem możemy policzyć gęstość średnią ze wzoru:

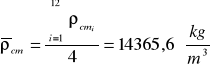
Rachunek błędów:

Uwzględniając klasę przyrządów odczyty są obarczone następującymi błędami:

• manometr M1:
  

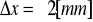
• manometr M2:
  

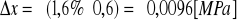
• manometr M3:
  

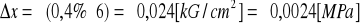
• manometr M4:
  

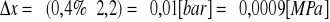
ROZKŁAD T-STUDENTA

Określenie wartości nadciśnienia w przewodzie na podstawie testu t-Studenta

Przyjęto poziom istotności α = 0,05, a tym samym poziom ufności 1-α = 0,95. Skorzystano z następujących wzorów:

• wyznaczenie średniej wartości pomiarów:

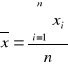
• wyznaczenie niepewności przypadkowej wartości średniej:

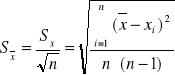
• wyznaczenie wartości odchylenia standardowego wartości średniej:

• wyznaczenie przedziału, w którym z określonym prawdopodobieństwem i dla założonego poziomu ufności powinna znajdować się wartość rzeczywista

gdzie:

- Odchylenie standardowe średniej pomiarów

α = 0,05 - przyjęty poziom istotności

1 -α - przyjęty poziom ufności

n - ilość pomiarów (n = 4)

t_{α, n-1} - współczynnik przyjęty z tablic rozkładu t-Studenta (t_{α, n-1} = 3,182)

- średnia wartość z odczytów [MPa]

x_i - i-ty odczyt z manometru [MPa]

Seria pomiarowa
1	0,1335	0,0012	0,1298	0,1372
2	0,1222	0,0015	0,1175	0,1269
3	0,1049	0,0037	0,0932	0,1168
4	0,0927	0,0014	0,0883	0,0972

Otrzymano przedziały ufności dla średniej wartości nadciśnienia w danej serii pomiarowej:

• Seria 1

[MPa]

• Seria 2

[MPa]

• Seria 3

[MPa]

• Seria 4

[MPa]

Wnioski i analiza wyników:

• Niepewność pomiaru zależy zarówno od klasy przyrządu jak i zakres pomiarowy. Zauważyliśmy, że najmniejsza niepewność występowała w manometrze 4.

• Jednocześnie na podstawie odczytów z tego manometru można zauważyć, że na odczyt nadciśnienia ma wpływ położenie manometru względem osi przewodu. Przyjeliśmy różne niepewności pomiaru położenia manometru względem osi przewodu.

• Z obliczeń gęstości wynika, że cieczą manometryczną była rtęć. Różnice w otrzymanych w trakcie obliczeń gęstościach wynikają z faktu, że do obliczeń tej gęstości wykorzystano odczyty nadciśnienia które są obarczone błędem. Ponadto sposób obliczania gęstości nie uwzględnia tego, że wysokość słupa wody nad cieczą manometryczną nie jest równa różnicy wysokości wskazań manometru.

• Dzięki Testowi T-Studenta zauważyliśmy, że dla pomiary z różnych manometrów dają różne przedziały w których znajduje się wartość rzeczywista nadciśnienia. Wynika to z tego, że każdy z użytych przyrządów charakteryzował się inną klasą, a co za tym idzie odczyty podawane były z różną dokładnością.