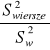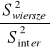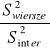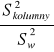WYKŁAD 1 08.10.2008

Statystyka - gałąź wiedzy zajmująca się zbieraniem, analizą, interpretacją danych numerycznych dotyczących agregatów złożonych i konkretnych jednostek.

Statystyka - sztuka wyciągania wniosków na podstawie niepełnych danych.

Biostatystyka - metodyka stosowania technik statystycznych w biologii i medycynie

Prawdopodobieństwo

Doświadczenie losowe - eksperyment, obserwacja zjawiska, którego wynik zależy od przypadku np. rzut monetą

Zdarzenie elementarne [ω] - każdy niepodzielny wynik doświadczenia losowego

Przestrzeń zdarzeń elementarnych [Ω] - zbiór wszystkich zdarzeń elementarnych. Przestrzeń taka może być zbiorem skończonym lub nieskończonym ale przeliczalnym ( przestrzeń skokowa lub dyskretna ) może też być zbiorem nieprzeliczalnym ( przestrzeń ciągła )

Zdarzenie losowe - każdy podzbiór przestrzeni zdarzeń elementarnych, może być jedno- lub wieloelementowy

Rodzina zdarzeń elementarnych - zbiór zdarzeń losowych związanych z tym samym zdarzeniem losowym

Zdarzeniami losowymi zajmuje się rachunek prawdopodobieństwa stanowiący matematyczny fundament statystyki

Rozróżnia się zdarzenia losowe:

- pewne

- niemożliwe

- prawdopodobne

Klasyczna definicja autorstwa Laplace'a

Prawdopodobieństwo wystąpienia danego zdarzenia jest równe ilorazowi liczby zdarzeń mu sprzyjających i liczby możliwych przypadków przy założeniu że wszystkie one są jednakowo możliwe i wzajemnie się wykluczają

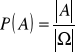
Definicja geometryczna

Rozwiązuje ona inny problem definicji klasycznej: niemożność stosowania w sytuacji gdy [A] i [Ω] są zbiorami nieskończonymi. W definicji geometrycznej liczebności tych zbiorów są zastępowane, np. polem powierzchni lub długością.

Definicja częstościowa von Misesa:

Utożsamia prawdopodobieństwo z granicą ciągu częstości. Oczywistą wadą tej definicji jest to, iż nic nie mówi ona o warunku istnienia owej granicy. Pojecie prawdopodobieństwa zostało sformalizowane przez Kołnogorowa? poprzez definicję aksjomatyczną. Prawdopodobieństwo zdarzenia jest liczbą rzeczywistą spełniającą pewne aksjomaty (twierdzenie przyjmowane bez dowodów). Jeżeli rozpatrujemy prawdopodobieństwo bez odniesienia do konkretnego zdarzenia to powinniśmy traktować ją jako funkcję.

Uproszczone podsumowanie aksjomatów i zależności z nich wynikające:

Zdarzenie	Objaśnienie	Prawdopodobieństwo
A	Zakres wartości	0≤P(A) ≤1 przy czym prawdopodobieństwu zdarzenia niemożliwego przyporządkowujemy 0, zaś zdarzenia pewnego 1
Nie A	Prawdopodobieństwo zdarzenia przeciwnego	P(A)'=1- P(A)
A lub B	Prawdopodobieństwo sumy ( alternatywy ) zdarzeń	P(A∪B)=P(A)+P(B)-P(A∩B) Jeżeli A i B są zdarzeniami wzajemnie się wykluczającymi to ostatni człon należy pominąć
A i B	Prawdopodobieństwo iloczynu ( koniunkcji ) zdarzeń	P(A∩B)=P(A/B)P(B)=P(B/A)P(A) Jeżeli zdarzenia A i B są niezależne to P(A∩B)=P(A)P(B)
A jeśli B	Prawdopodobieństwo warunkowe	P(A/B)= P(A∩B)/P(B) Dla P(B)=0

Doświadczenie losowe o dwuelementowej przestrzeni wyników zwanych sukcesem i porażką, których prawdopodobieństwa sumują się do 1

p - sukces

q - porażka

q=1 - p

Takie doświadczenie to próba Bernoulliego. Seria n niezależnych powtórzeń próby Bernoulliego w tych samych warunkach nazywa się schematem Bernoulliego o n próbach. Prawdopodobieństwo k sukcesów w n próbach Bernoulliego obliczymy wzorem:

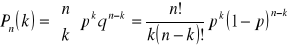
Filozoficzne podstawy prawdopodobieństwa są od kilku stuleci przyczyną gorących dyskusji. Główna linia frontu przebiega pomiędzy zwolennikami pojmowania prawdopodobieństwa jako czegoś obiektywnego wynikającego z nieprzewidywalności wyniku a tym wyraża ono miarę opartą na pewnej wiedzy w ocenie to czy coś jest prawdą czy nie.

W drugim przypadku określenie interpretacji jako subiektywistycznej narzuca się samo. Korzenie dwóch dominujących obecnie szkół (częstościowej i Bayesowskiej) tkwią upraszczając przedstawionych powyżej podejściach filozoficznych.

Chcąc dokonać charakterystyki zdarzeń podobnych lub nieokreślonych najlepiej posługiwać się zmienną losową - funkcją przypisującą liczby zdarzeniom losowym X. Mówimy o zmiennej skokowej (dyskretnej) jeśli jej zbiór wartości jest skończony lub nieskończony lecz przeliczalny, zaś o zmiennej ciągłej gdy jest nieskończony i nieprzeliczalny. Zbiór prawdopodobieństwa odpowiadający wszystkim możliwym wartościom zmiennej nazywa się rozkładem prawdopodobieństwa tej zmiennej. Prawdopodobieństwa muszą się sumować do 1. Najprościej sprawa wygląda w przypadku gdzie rozkład zmiennej jest zbiorem par wartości prawdopodobieństwa. Można to wyrazić graficznie lub tabelą. Sytuacja komplikuje się gdy jest zmienna losowa jest ciągła bo sumaryczne prawdopodobieństwo równe 1, mówiąc kolokwialnie, musi zostać rozdzielone pomiędzy nieskończoną liczbę wartości. Z tego wynika, że prawdopodobieństwo przyjęcia konkretnej wartości równa się 0. W celu przezwyciężenia tej trudności wprowadzono pojęcie funkcji gęstości prawdopodobieństwa f(x). Jest ona określona w zbiorze liczb rzeczywistych przyjmuje wyłącznie wartości nieujemne, a ponadto zachodzi prawidłowość: prawdopodobieństwo przyjęcia przez zmienną x wartości z przedziału (a,b) jest równe polu obszaru ograniczonego wykresem funkcji gęstości prostymi x=a, x=b oraz osią odciętych (OX).

-

Rozkłady prawdopodobieństwa zmiennych losowych są modelami teoretycznymi rozkładów populacji gdzie przez zmienną rozumie się rozpatrywaną cechę elementów wyróżnionego zbioru (np. długość, wiek). Rozkład prawdopodobieństwa zmiennej losowej można przekształcić w tzw dystrybuantę F(x), która jest funkcją kumulacyjną wyrażającą prawdopodobieństwo zdarzenia polegającego na przyjęciu przez zmienną X wartości z przedziału (-∞ do X).

-

WYKŁAD 2 15.10. 2008

Wybrane przykłady zmiennych losowych dyskretnych:

1. rozkład jednostajny - zmienna losowa przyjmuje wszystkie swoje wartości z tym samym prawdopodobieństwem np. rozkład zmiennej której wartościami są liczby oczek przy jednostajnym rzucie

2. rozkład Bernoulliego czyli dwumianowy - zmienna losowa X przyjmuje wartości k=0,1,2,3,...,n z prawdopodobieństwem wyliczanym ze wzoru:

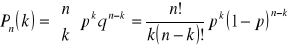
Innymi słowy jest to rozkład opisujący liczbę sukcesów w ciągu n niezależnych prób , z których każda ma stałe prawdopodobieństwo sukcesu równe k. Rozkład ten zależy od dwóch parametrów p,n. Rozkład jest symetryczny wyłącznie dla p=0,5, np. liczba orłów wyrzuconych w trakcie dwukrotnego rzutu monetą.

3. dla dużego n, ale małego p czyli n ≥ 50, p ≤0,1 rozkład dwumianowy może zostać zastąpiony rozkładem Poissona (rozkład rzadkich zdarzeń). Zmienna losowa przyjmuje wartości k=0,1,2,3....itd., z prawdopodobieństwami wyliczonymi ze wzoru:

Rozkład ten zależy od jednego parametru
( średnia wartość zdarzeń sprzyjających) np. rozmieszczenie gniazd w przestrzeni, rozmieszczenie zwierząt na danym terenie.

Inne rozkłady zmiennych losowych:

-rozkład normalny,

-rozkład t-Studenta,

-rozkład F Fishera-Snedecora,

-rozkład chi-kwadrat

Zmienna to rozpatrywana....

Zbiór wszystkich możliwych wartości danej zmiennej nosi nazwę zbiorowości generalnej lub populacji (w sensie statystycznym). Może być owa populacja zarówno rzeczywista jak i hipotetyczna. Populacje rzeczywiste charakteryzują się posiadaniem skończonej liczby możliwych wartości zmiennych, np. długość ogona lisów na danym terenie.

Populacje hipotetyczne odznaczają się posiadaniem nieskończonej lub niezwykle dużej liczby posiadanych możliwych wartości zmiennych.

Populacja rzeczywista

Najczęściej uzyskiwane informacje na temat populacji na podstawie wszystkich jej elementów jest niemożliwe lub niepraktyczne. Jedynym rozwiązaniem jest zbadanie próby populacji. W doborze próby istotne jest aby była ona reprezentatywna dla danej populacji. Jest to warunkiem wiarygodności wyników badań. Jednym z rozwiązań preferowanych np. w biostatystyce jest wybór próby probabilistycznej lecz takiej, o której możemy powiedzieć że każdy element populacji ma określone prawdopodobieństwo znalezienia się w próbie. Najprostszym sposobem wyznaczenia próby probabilistycznej jest prosta próba losowa. Każdy element ma równe i niezerowe możliwości aby się w tej próbie znaleźć. Próby losowe dobieramy w drodze losowania. Losowanie z rzeczywistej populacji może być wykonane na dwa sposoby:

• z powtórzeniami ze zwracaniem ( losowanie niezależne )

• bez powtórzeń, bez zwracania, element populacji może być brany do próby tylko raz ( losowanie zależne)

Wstępne procedury statystyczne zakładają że próba została wylosowana z powtórzeniami lub że populacja jest na tyle duża w stosunku do próby że sposób losowania, tzn. zależne czy niezależne nie ma dużego znaczenia. Wybór próby losowej z nieskończonej populacji (hipotetycznej) powinien być dokonany w taki sposób aby wyniki obserwacji lub pomiarów odnosiły się do niezależnych powtórzeń doświadczeń w określonych warunkach. Reprezentatywność próby losowej jest związana z jej wielkością- ze wzrostem próby wzrasta jej reprezentatywność.

Typy danych w biologii.

W biologii i nie tylko wyróżniamy cechy inaczej zmienne: jakościowe czyli niemierzalne, porządkowe, ilościowe czyli mierzalne.

W przypadku zmiennych jakościowych posługujemy się skalą nominalną np. stosując kryterium płci, taksonomiczne grupy krwi A,B.

Więcej informacji dostarczają nam zmienne porządkowe, w ich przypadku dysponujemy rangami przypisanymi poszczególnym stanom zmiennych. Możemy więc te stany zestawić w pewnym porządku.

Zmienne mierzalne czyli ilościowe jesteśmy je w stanie wyrazić przy pomocy jednostek miary w jednej skali, czyli możemy zastosować skale interwałową, np. masa, długość, ilość erytrocytów we krwi. Dane pochodzące z policzenia wyrażane są przez liczby naturalne (zmienna skokowa) zaś dane przedstawione w postaci liczb rzeczywistych - pomiary skalarne. (zmienna ciągła).

Możliwa jest zamiana skali ale tylko w dół, np. interwałowej na porządkowa.

Są jeszcze typy złożone: procenty ( proporcja pomnożona przez 100), proporcje (proporcja samców w populacji ≈ 0,5) i stosunki liczbowe (1:2).

Statystyka opisowa

Działem statystyki poświęconym metodom opisu danych statystycznych jest statystyka opisowa. Metody te mają za zadanie taki opis danych aby rezygnując ze zbędnych szczegółów podsumować je podkreślając istniejące tendencje. Istotą statystyki opisowej jest więc formułowanie uogólnień na temat zbioru danych kosztem niepotrzebnych informacji szczegółowych. Dane statystyczne można opisać, podsumować na kilka sposobów:

• tabelarycznie

• graficznie

• poprzez wyznaczanie miar rozkładów

Rezultatem przeprowadzonych badań jest zazwyczaj nieuporządkowany zbiór liczb, który w przypadku elementów wchodzących w skład pojedynczej próby nosi nazwę szeregu statystycznego. Taki szereg najlepiej jest uporządkować np. posortować w porządku rosnącym przypisując konkretnym wartościom odpowiadającym frekwencji czyli częstości. Otrzymamy w ten sposób szereg rozdzielczy. Najlepiej przedstawić go w postaci tabeli ewentualnie wzbogacając je o dodatkowe kolumny: częstości względne, skumulowane. Tabelaryczny rozkład szeregu statystycznego czyli szereg rozdzielczy można w prosty sposób przedstawić za pomocą wykresu. W przypadku małej liczby danych na osi poziomej lub pionowej zaznaczamy wartości pomiaru w postaci kreski, której długość odzwierciedla liczbę pomiarów o określonej wartości. Jeśli dysponujemy próbami o dużej liczebności praktyczne jest pogrupowanie w przedziały klasowe.

Należy więc zmodyfikować tabelę. Kreski zostają zastąpione przez przylegające do siebie prostokąty, których szerokość odpowiada poszczególnej szerokości klasy, zaś jej wysokość liczebności lub częstości względnej. Wprowadzenie drugiej osi jest niezbędne. Wykres to histogram. Jeśli przedstawiony w sposób graficzny rozkład liczebności zmiennej w sposób nieciągły stosujemy nie histogram, ale tzw. wykres słupkowy - słupki nie przylegają do siebie.

W wyniku przeprowadzonych badań otrzymujemy najczęściej zbiór liczb. Jeżeli chcemy na ich podstawie wnioskować o pewnej zbiorowości generalnej muszą one stanowić próbę reprezentatywną dla tej populacji. Zakładając to częstości względne populacji, apsokrymowane przez ich odpowiedniki w próbie można traktować jako prawdopodobieństwo w teoretycznym rozkładzie zmiennej losowej, gdyż stanowi on model teoretyczny rozkładu populacji.

W większości przypadków jest niezbędny opis liczbowy obserwowanego rozkładu częstości, wartości liczbowe, a więc pewne miary dostarczające w sposób syntetyczny informacji na ten temat, noszą nazwę parametrów ( jeśli dotyczą populacji, oznaczamy zazwyczaj literami alfabetu greckiego) lub statystyk ( jeśli dotyczą próby, oznaczamy zazwyczaj literami alfabetu łacińskiego ) tak więc w przypadku próby losowej wartości statystyk stanowią przybliżenia wartości parametrów. Często używa się pojęcia statystyki opisowej.

Statystyki opisowe dzielimy na kilka grup:

1) Miary położenia - wskazują miejsce , wartości, najlepiej reprezentujące wszystkie wartości zmiennej, ważną podgrupę miar położenia stanowią tzw. miary tendencji centralnej, dostarczają informacji o typowym poziomie wartości zmiennej. Miary położenia: średnia arytmetyczna, geometryczna, ważona, harmoniczna, kwantyle (kwantyl pierwszy, drugi, trzeci), decyle, centyle, wartość modalna (moda, dominanta).

Średnie, modę i medianę można też określić mianem miar tendencji centralnej.

Symbolika:

x₁=2,13, x₂= 3,56, x₃= 5,66, N=3

Średnie:

a) średnia arytmetyczna

Najlepiej dla zmiennych o rozkładzie przynajmniej z grubsza symetrycznym. Średnią podajemy z dokładnością do jednego miejsca po przecinku większą niż surowe dane.

b) Średnia ważona

Stosujemy gry pomiary nie są równocenne, czyli przy obliczaniu średniej ze średnich wyliczonych z prób o różnej wartości.

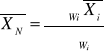
c) Średnia geometryczna

Przydatna w przypadku rozkładów prawostronnie skośnych, a szczególnie gdy chcemy uzyskać informacje na temat średniego tempa zmian. Nie może być stosowana gdy przynajmniej jedna z wartości jest ujemna.

d) Średnia harmoniczna

Stosowana do obliczania średniej z rozmiarów k-prób o rozmiarach n₁,......, n_k. Można stosować do liczb dodatnich.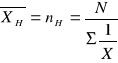

Moda (wartość modalna) - najczęściej występująca wartość zmiennej, niekiedy lepiej stosować przedział modalny zamiast pojedynczych wartości. Moda jest miarą niestabilną. Jedna wartość może mieć bardzo istotny wpływ.

Mediana - wartość spełniająca następujący warunek: przynajmniej połowa danych jest od niej mniejsza lub jest jej równa, zaś połowa danych jest od niej większa lub jest jej równa. Jest nieczuła na wartości skrajne.

WYKŁAD 3 22.10.2008

Drugą grupę miar położenia stanowią kwantyle, czyli wartości posortowanego szeregu statystycznego ułożone w taki sposób, że dzielą go na określone części pod względem liczby elementów składowych. Części te pozostają do siebie określonych proporcjach. Najczęściej używa się kwartyli - dzielą szereg na 4 części, decyli - dzielą na 10 części, imbecyli i centyli - dzielą szereg na 100 części.

Mediana jest drugim kwartylem i 50 centylem.

Wyznaczanie kwartyli - metoda Turkey'a:

1. uporządkuj dane od najmniejszej do największej

2. podziel dane na dwie części znajdując medianę Q₂

3. znajdź medianę dla małych wartości Q₁

4. znajdź medianę dla dużych wartości Q₃

np.

• 2 3 4 5 1 2 3 (3.5) 4 5 6

Q₁ Q₂ Q₃ Q₁ Q₂ Q₃

Miary zmienności i rozproszenia

Najprostsza miara jest rozstęp R, czyli różnica między największa i najmniejszą wartością. Istnieje też rozstęp kwartylowy, inaczej odchylenie ćwiartkowe IQR. Najczęściej używanymi miarami tego typu są wariancja i odchylenie standardowe. Obie oparte są na odchyleniach od wartości średniej. Im większa wariancja lub odchylenie standardowe tym większa jest zmienność danych.

Wariancja σ²(oznaczenie dla parametru), s²(oznaczenie dla statystyki) jest średnią arytmetyczną kwadratów odchyleń.

odchylenie od średniej

Pierwiastek kwadratowy z wariancji nosi nazwę odchylenia standardowego. Jego zaletą jest to, że wynik podaje się w jednostkach takich samych jak surowe dane.

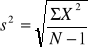
Wariancję raportujemy z dokładnością dwukrotnie większą niż dokładność średnia. Dokładność odchylenia standardowego jest taka sama jak dokładność średnia.

Są to miary najbardziej użyteczne w rozkładach symetrycznych. Jeżeli odchylenie standardowe podzielimy przez średnią to uzyskamy tzw współczynnik zmienności V (podawany w %). Umożliwia porównywanie zmienności w populacjach różniących się zasadniczo zmiennymi. W praktyce podając syntetyczną charakterystykę należy odnotować następujące statystyki opisowe:

- liczebność próby

- miary lub miarę tendencji centralnej

- miary lub miarę rozproszenia.

W przypadku rozkładu symetrycznego będzie to najczęściej średnia arytmetyczna i odchylenie standardowe. A w przypadku skośnych - mediana, odchylenie ćwiartkowe i kwartyle. Graficznie prezentuje się dane w postaci wykresu ramkowego inaczej skrzynkowego.

Miary asymetrii i koncentracji

Współczynnik asymetrii pozwala określić siłę i kierunek asymetrii.

Dla A_s = 0 symetryczny

A_s > 0 asymetria prawostronna

A_s < 0 asymetria lewostronna

Kurtoza (K) dotyczy koncentracji (rozkład skupiony czy rozproszony)

K < 0 rozkład bardziej spłaszczony od normalnego

K > 0 rozkład bardziej wysmukły od normalnego

Wnioskowanie statystyczne - estymacja

Zagadnieniami związanymi z uogólnianiem próby losowej na zbiorowość generalną, jak również szacowania nieodłącznie związanych z tym błędów zajmuje się dział statystyki zwanej wnioskowaniem statystycznym. Może być również zdefiniowany jako proces wnioskowania o zbiorowości generalnej na podstawie próby z określonym poziomem pewności. W skład technik wnioskowania statystycznego wchodzą metody estymacji, czyli szacowania nieznanych wartości parametrów populacji. Jest to tzw. estymacja parametryczna. Istnieje też estymacja nieparametryczna - rzadko stosowana.

Jeżeli oszacowaniem wartości badanego parametru jest liczba to mówimy o estymacji punktowej. Jeśli w celu oszacowania wyznaczamy przedział liczbowy to używamy terminu estymacja przedziałowa. Z estymatorami punktowymi spotkaliśmy się przy statystyce opisowej. Wyliczone na podstawie próby reprezentatywnej są estymatorami parametrów odpowiedniej populacji. W praktyce użyteczne są takie estymacje, które cechują określone właściwości:

- nieobciążoność - wartość przeciętna = wartości szacowanego parametru

- efektywność - estymator ma małą wariancję

- zgodność - zwiększenie liczebności próby powoduje spadek ryzyka popełnienia błędu.

Chcąc poznać przedział do którego z określonym prawdopodobieństwem (najczęściej 95%) należy szukana wartość parametru należy skonstruować przedział ufności (podstawowe pojęcie estymacji przedziałowej!). Owo określone prawdopodobieństwo nosi nazwę poziomu ufności 1-α, gdzie α- dopuszczalne prawdopodobieństwo popełnienia pomyłki (α - inna nazwa: poziom istotności).

1. im węższy otrzymany jest przedział ufności tym dokładniejszym oszacowaniem wartości parametru jest wartość jego estymatora czyli statystyki.

2. Podniesienie poziomu ufności skutkuje zwiększeniem szerokości przedziału ufności, czyli zmniejszeniem precyzji estymacji. Pewnym, chociaż często nie realnym, rozwiązaniem tego problemu jest zwiększenie liczebności próby.

Rozkład normalny (Gaussa) stanowi przybliżenie rozkładu dwumianowego dla dużych wartości N. Także rozkład Poissona wraz ze wzrostem parametru λ coraz bardziej upodabnia się do rozkładu normalnego. Ponadto rozkład wielu zmiennych ze świata rzeczywistego jest zbliżony do teoretycznego rozkładu normalnego, np. wzrost mężczyzn, długość łodygi roślin.

Rozkład normalny należy do grupy rozkładów ciągłych. Kształt funkcji gęstości jest wyznaczany przez dwa parametry: wartość oczekiwaną inaczej średnią (μ) i wariancję σ². Pierwszy z nich decyduje o położeniu krzywej względem osi X, drugi o smukłości krzywej.

Rozkład normalny o średniej równej 0 i wariancji równej 1 nosi nazwę rozkładu normalnego standaryzowanego - rozkład Z. Aby go uzyskać należy dokonać standaryzacji zmiennej X.

A w przypadku próby:

Dzięki standaryzacji możemy określić stosunek pojedynczego pomiaru do średniej i rozproszenia. Dla rozkładu normalnego standaryzowanego powierzchnie pod krzywa gęstości odpowiadające określonym całkom oznaczonym są stabelaryzowane.

Cechy rozkładu normalnego:

- symetryczny względem średniej (wartości oczekiwanej)

- wartość średnia to jednocześnie moda i mediana

- obowiązuje reguła 3 σ - 68,27% pola powierzchni pod krzywą funkcji gęstości leży w granicach 1σ od średniej, 95,45% w odległości 2σ, a 99,73% w odległości 3σ od średniej. Można zauważyć, że 95% pola powierzchni leży w granicach 1,96 odchylenia od średniej.

Rozważmy populację o dowolnym rozkładzie, średniej μ i odchyleniu standardowym σ. Jeżeli pobierzemy z tej populacji duże próby losowe niezależne, to rozkład średnich z tych prób będzie zgodny z rozkładem normalnym o średniej μ i odchyleniu standardowym σ/√N. Jeśli wprowadzimy dodatkowe założenie, że populacja ma rozkład normalny to przedstawiona wcześniej prawidłowość będzie obowiązywała także w przypadku małych losowych niezależnych prób. Jest to jeden ze sposobów przedstawiania Centralnego Twierdzenia Granicznego, które mówi, że ze wzrostem wielkości próby rozkład ze średnich prób zmierza w kierunku rozkładu normalnego. Wspomniane σ/√N nosi nazwę błędu standardowego średniej. O ile zwykłe odchylenie standardowe (σ, s) jest miara niepewności, z którą średnia z próby estymuje poszczególne wartości, o tyle błąd standardowy średniej jest miarą niepewności z jaką średnia z próby estymuje średnią z populacji generalnej. Innymi słowy jest to syntetyczna miara błędu estymacji średniej. Średnia obarczona mniejszym błędem lepiej estymuje średnią z populacji niż średnia z dużym błędem.

Ważnym polem zastosowań praktycznych błędów jest konstruowanie przedziałów ufności. Jeśli znamy odchylenie standardowe w populacji σ to 95% przedział ufności dla średniej (95% CI) konstruujemy w sposób następujący: pobieramy próbę losową, obliczamy średnią i błąd standardowy wg wzoru:

, po czym przedział konstruujemy:

W przypadku 95% CI Z=1,96.

Bardzo rzadko znamy wartość odchylenia standardowego w populacji.

Zazwyczaj musi nam wystarczyć przybliżenie wyliczone na podstawie próby s. jeśli próba jest 100-elementowa możemy do wzoru na błąd standardowy podstawić wartość odchylenia standardowego z próby i obliczenia wykonać zgodnie z powyższym wzorem.

Jeśli natomiast próba jest mała, czyli prawie zawsze, to musimy w obliczeniach zastąpić rozkład normalny rozkładem t-Studenta. Opisaną dalej procedurę możemy stosować dla dużych prób, a dla małych musimy.

Rozkład t-Studenta jest kolejnym rozkładem zmiennej losowej ciągłej. Przy dużych wartościach N zbliża się do rozkładu normalnego, a dla małych wielkości prób jest bardziej spłaszczony. Jeśli byśmy z populacji o rozkładzie normalnym pobierali próby N-elementowe i dla każdej próby obliczali statystykę t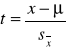
(błąd obliczony na podstawie błędu odchylenia standardowego z próby) to rozkład statystyki t byłby zgodny z rozkładem t-Studenta dla N-1 stopnia swobody. Rozkład ten jest symetryczny i zależy tylko od jednego parametru - stopni swobody(df, ν). Wzór pozwalający na wyznaczenie przedziału ufności małej średniej i przy nieznanej wartości odchylenia standardowego w populacji, czyli prawie zawsze, wyznaczamy ze wzoru:

X±(t_{N-1, 1- α/2})*(S_x)

WYKŁAD 4 29.10.2008

Weryfikacja hipotez statystycznych - sprawdzanie sadów o zbiorowości generalnej powstałych w oparciu o badania częściowe.

Jeśli hipoteza statystyczna dotyczy wartości parametrów populacji, np. średniej jest nazywana hipotezą parametryczną, w przeciwnym razie mówimy o hipotezie nieparametrycznej. Procedura postępowania w trakcie weryfikacji hipotezy statystycznej nazywa się testem statystycznym. Rozróżniamy testy parametryczne i nieparametryczne. Pierwsze z nich służą do weryfikacji hipotez parametrycznych i wymagają przyjęcia założeń co do typu rozkładu badanej cechy. Punktem wyjścia w trakcie weryfikacji hipotezy statystycznej jest przyjęcie założeń, czyli modelu i hipotezy. Podział założeń pomiędzy model i hipotezę może być zróżnicowany w zależności od problemu badawczego(patrz: Łomnicki rozdz. 4.4 pkt1).

Założenia modelu mogą być następujące:

- niezależna próba losowa /próby losowe o określonej wielkości

Następnie formułujemy hipotezę, którą poddamy weryfikacji tzw. hipotezę zerową H₀. najczęściej zakłada ona brak różnic, może tez zakładać przyjęte wartości parametru, ale nie jest to regułą. Hipoteza przeciwstawna do weryfikowanej nosi nazwę hipotezy alternatywnej H_A lub H₁, niekiedy zwana tez hipotezą badawczą. Hipotezę alternatywna przyjmujemy gdy odrzucimy hipotezę zerową.

H₀ : μ₁ - μ₂ = 0 lub H₀: μ₁= μ₂

Inne przykłady:

H₀ : μ₁= 0

H₀ : μ₁= μ₂=μ₃

H₀ : σ₁=σ₂

Możliwe alternatywne hipotezy:

H₀ : μ₁ ≠μ₂ (test dwustronny)

H₀ : μ₁< μ₂ (test jednostronny)

H₀ : μ₁> μ₂ (test jednostronny)

W testach dwustronnych nie interesuje nas kierunek …., są one preferowane w biologii. Podczas weryfikacji hipotez statystycznych popełnić można dwa rodzaje błędów, możemy:

1) odrzucić hipotezę zerową mimo, że jest ona prawdziwa - popełniamy wtedy błąd pierwszego rodzaju. Największe dopuszczalne przez badacza ryzyko popełnienia błędu pierwszego rodzaju nosi nazwę poziomu istotności α, zwane też poziomem istotności exante, najczęściej przyjmowany poziom to 0,05 (α=0,05).

* spotykamy się tez z tzw. poziomem prawdopodobieństwa, przez niektórych niezbyt prawidłowo określany poziomem istotności expost lub poziomem komputerowym (P, P-value, P-wartość).

P-wartość prawdopodobieństwo, że obserwowane różnice są dziełem przypadku, jest to najmniejszy ustalony poziom na którym może być odrzucona hipoteza zerowa. Mała wartość P świadczy o tym, że jeśli hipoteza zerowa jest prawdziwa to obserwowana różnica, a także jeszcze większe możliwe różnice są mało prawdopodobne, zaś hipoteza alternatywna dostarcza bardziej sensownego wyjaśnienia.

P-wartość zwracają procedury w pakietach statystycznych, ale można je uzyskać z tabel statystycznych

2) nie odrzucić hipotezy zerowej, mimo że jest ona fałszywa. Popełniamy wtedy błąd II rodzaju.

H0 / decyzja	Nie odrzucenie H0	Odrzucenie H0
H0 jest prawdziwa	Decyzja prawidłowa	Błąd I rodzaju
H0 jest fałszywa	Błąd II rodzaju (β)	Decyzja prawidłowa

Drugim etapem weryfikacji hipotezy jest wybór statystyki testowej, czyli miary dla badanego i wyznaczenie jej rozkładu przy założeniu, że hipoteza zerowa jest właściwa. Ten etap nosi nazwę otrzymywania rozkładu z prób(nazwa z Łomnickiego). Następnie przyjmujemy poziom istotności testu i wyznaczamy obszar krytyczny - zbiór albo zakres wartości statystyki opisowej przy których odrzucamy hipotezę zerową na korzyść hipotezy alternatywnej. Znajduje się zawsze na krańcach rozkładu. Obejmuje te wartości, których prawdopodobieństwo przy założeniu prawdziwości hipotezy zerowej jest bardzo małe. Obszar może być dwustronny, lewo- lub prawostronny i jest oddzielony od pozostałej części rozkładu przez wartości krytyczne. Można je odczytać z tablic rozkładu przy danym poziomie α. Położenie obszaru krytycznego zależy od postaci hipotezy alternatywnej.

-

Kolejnym etapem jest przeprowadzenie badań i obliczenie wartości statystyki testowej na podstawie próby albo prób. Na koniec podejmujemy decyzję:

• jeżeli korzystaliśmy z tablic statystycznych to na danym poziomie istotności alfa hipotezę zerową odrzucamy na korzyść hipotezy alternatywnej, gdy statystyka testowa obliczona na podstawie próby znalazła się w obszarze krytycznym, w przeciwnym razie(gdy znalazła się w obszarze akceptowalnym) stwierdzamy, że na danym poziomie istotności nie mamy podstaw do odrzucenia hipotezy zerowej.

• Jeśli korzystamy z komputerowego pakietu statystycznego to wypluwa on P-wartość, gdy

P≤α odrzucamy hipotezę zerową na korzyść hipotezy zerowej, P ≥ α nie ma podstaw do odrzucenia hipotezy zerowej.

Test, który ma na celu określenie prawdopodobieństwa, że dany wynik nie jest dziełem przypadku nosi nazwę testu istotności.

Moc testu - oznacza się jako 1-β, zdolność testu do unikania błędu drugiego rodzaju. Jest to prawdopodobieństwo odrzucenia hipotezy zerowej, gdy jest ona fałszywa. Zwiększenie wielkości próby powoduje dla ustalonego α i dla danej hipotezy zerowej wzrost mocy testu. Moc testu może być dokładnie określona dla konkretnej hipotezy alternatywnej. Zakłada się, że test powinien mieć moc równą 0,80. Na ogół testy parametryczne maja moc większą od swoich odpowiedników nieparametrycznych, jeśli są spełnione wymagania dla testów parametrycznych. Test mocny, to taki, który w większości przypadków umożliwia odrzucenie fałszywej hipotezy zerowej.

Porównywanie dwóch średnich - testy t-Studenta

Jeśli dysponujemy niezależną próbą losowa o rozkładzie normalnym to możemy przetestować hipotezę zakładającą, że średnia z populacji z której pochodzi ta próba jest równo określonej wartości przy pomocy testu t-Studenta dla pojedynczej próby.

Jeśli hipoteza zerowa jest prawdziwa to statystyka testowa t ma rozkład zgodny z rozkładem t-Studenta dla N-1 stopnia swobody.

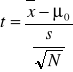
Rozkład t-Studenta może być także stosowany do porównywania dwóch średnich z populacji, pod warunkiem, ze obie populacje maja rozkłady zgodne z normalnym, zaś odchylenia lub wariancje w populacji są równe(musimy dysponować dwiema niezależnymi próbami losowymi) - test nosi nazwę testu t-Studenta dla dwóch prób niezależnych (niepowiązanych).

Hipotezy możemy zapisać następująco:

Dla dwóch prób: H₀ : μ₁=μ₂ dla jednej próby: H_{0 :} μ=μ₀

H_A : μ₁≠μ₂ H_A: μ≠μ₀

μ₁>μ₂ μ>μ₀

μ₁<μ₂ μ<μ₀

Aby uzyskać najlepsze oszacowania wspólnego odchylenia standardowego należy w odpowiedni sposób połączyć odchylenia standardowe policzone dla obu prób

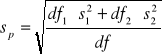
df₁ = N₁ - 1, df₂ = N₂ - 1, df = df₁+df₂

Błąd standardowy różnicy średniej

,

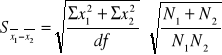
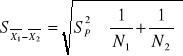
Statystyka opisowa przyjmuje taka wartość:

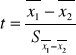
, df = N₁ - N₂ - 2 = df₁ + df₂

Gdy nie możemy założyć jednorodności wariancji sprawa się komplikuje i nie można obliczyć wspólnego oszacowania odchylenia standardowego lub wariancji i błąd standardowy różnicy średnich wyznaczany jest w oparciu o wzór:

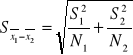
Nie możemy także stosować standardowej tablicy wartości krytycznych rozkładu t. W przypadku gdy wielkości prób są sobie równe, brak normalności nie stanowi problemu, zaś test działa dobrze nawet w przypadku gdy odchylenia różnią się znacznie, natomiast różna skośność ma wysoce negatywny wpływ na wiarygodność wyników. Nie zawsze jednak dwie próby, które nas interesują można określić jako niezależne albo nie powiązane ze sobą. Z taką sytuacja możemy się spotkać np., gdy rozpatrujemy ta sama grupę, ale badana dwukrotnie. Pojawiają się tzw. pary wiązane.

WYKŁAD 5 05.11.2008

Pary wiązane

Tworzenie takich par nie musi się ograniczać do wspomnianego sposobu(patrz: Łomnicki rozdz. 7.1).

Jeśli dla każdej pary obliczamy różnice d to otrzymamy zbiór N różnic co możemy potraktować jako próbę i przetestować czy wartość średnia(średnia różnica) istotnie odbiega od zera. Tzn. czy niezależna próba losowa ze wszystkich możliwych różnic, które byśmy otrzymali w przypadku powtórzenia eksperymentu dla nieskończonej liczby par wiązanych pochodzi z populacji o wartości oczekiwanej równej zero. Co można wyrazić w sposób bardziej biologiczny - brak różnic między zabiegiem a kontrolą albo badany lek nie powoduje istotnego spadku stężenia cukru(pomiar wykonany w stosunku do tej samej liczby osób przed i po podaniu leku). Jest to test t dla prób zależnych, powiązanych albo dla par wiązanych. Obowiązuje założenie normalności rozkładu różnic, a przynajmniej symetria tego rozkładu. Jednorodność wariancji sprawdzać nie musimy.

Hipotezy wyglądają w sposób następujący:

H₀ : μ_d=0

H_A : μ_d≠0

μ_d>0

μ_d<0

,

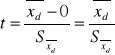
df = N-1, gdzie N- liczba par

Transformacja danych

Są to takie przekształcenia, które wpływają na kształt rozkładu. Stosujemy je w przypadku, gdy nasze dane nie spełniają założeń, np. brak normalności rozkładu, wariancji. Dla danego testu stosujemy taką samą transformację w stosunku do wszystkich prób.

Transformacje danych:

1. zmniejszanie skośności w przypadku rozkładów prawoskośnych

- logarytmujemy pomiary (lg lub ln)

- pierwiastkujemy

2. zmniejszanie skośności w przypadku rozkładów lewoskośnych

- obliczamy antylogarytmy (Y=e^x lub Y=10^x)

- podnosimy do kwadratu lub sześcianu (przy małej skośności).

Często transformacje te są jednocześnie przydatne w przypadku niejednorodnych wariancji (szczególnie logarytmowanie).

Inne zalecane:

-

-

-

-

-

Test F i wprowadzenie do analizy wariancji ANOVA

Testem F nazywamy każdy test statystyczny wykorzystujący statystykę testową, która przy założeniu prawdziwości hipotezy zerowej ma rozkład zgodny z rozkładem F. Rozkład F zwany rozkładem Fishera-Snedecora jest kolejnym rozkładem zmiennej losowej ciągłej. W przeciwieństwie do wszystkich poznanych rozkładów ciągłych jest on prawostronnie skośny, zaś jego kształt zależy od dwóch parametrów, zwanych stopniami swobody. Unikając formalnej definicji można powiedzieć, że jest to rozkład ilorazu wariancji.

Załóżmy, że z populacji o rozkładzie normalnym losowalibyśmy wielokrotnie po dwie próby o liczebności odpowiednio N₁ i N₂. Wyliczane ilorazy wariancji z obu prób miałyby wówczas rozkład zgodny z rozkładem F o stopniach swobody N₁-1 i N₂-1. Rozkład F otrzymalibyśmy w sytuacji, gdy losowane próby pochodziłyby z dwóch różnych populacji, tzn. populacji różniących się średnimi o rozkładach zgodnym z rozkładem normalnym pod warunkiem, że ich parametryczne wariancje, czyli wariancje w tych populacjach byłyby równe. Rozkład ten jest często wykorzystywany do testowania hipotezy o jednorodności wariancji, czyli braku różnic miedzy wariancjami. W przypadku dwóch niezależnych prób losowych z populacji o rozkładzie normalnym powszechnie stosowanym (obecnie coraz rzadziej) jest test F braku różnic między dwiema wariancjami.

H : σ₁² = σ₂²

H : σ₁² ≠ σ₂²

Statystyka testowa:

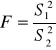
(w liczniku zawsze wartość większa)

Zakładając, że hipoteza zerowa jest prawdziwa, F ma rozkład zgodny z rozkładem F Fishera-Snedecora o następującej kombinacji liczby stopni swobody:

df = N-1 dla większej wariancji (główka tablicy wartości krytycznych)

df = N-1 dla mniejszej wariancji (pierwsza kolumna tablicy wartości krytycznych)

UWAGA! Testując hipotezę zerową na poziomie α stosujemy tablicę wartości krytycznych dla α/2.

Hipotezę zerową odrzucamy, gdy obliczana statystyka jest równa lub większa od wartości krytycznej.

Tabele zawierają wartości krytyczne wyłącznie dla prawego skrzydła rozkładu.

Wymusza to umieszczenie większej wariancji w liczniku, co skutkuje dwukrotnym wzrostem prawdopodobieństwa przekroczenia wartości krytycznej.

Dlatego testując na poziomie istotności α używamy tablic dla poziomu istotności α/2.

Zalecaną alternatywa dla tego testu jest test Lerene'a.

Test F można także stosować do weryfikacji hipotezy głoszącej, ze wartości średnie dla dwóch lub więcej populacji o rozkładzie zgodnym z rozkładem normalnym są równe, zakładając, że populacje te nie różnią się wariancjami. Innymi słowy dysponując kilkoma niezależnymi próbami losowymi z populacji o rozkładzie normalnym możemy przeprowadzić test hipotezy głoszącej, że pochodzą one z populacji nie różniącymi się średnimi lub z tej samej populacji. Zagadnienie to stanowi najprostszy problem rozpatrywany podczas tzw. analizy wariancji czyli ANOVA. Nazwa tej techniki bierze się stąd, że jej istotą jest podział zmienności całkowitej obserwowanej w uzyskanych wynikach pomiarów na kilka komponentów (przynajmniej dwa), które są ze sobą porównywane.

Rozpatrzmy najprostszy przypadek ANOVY, czyli jednoczynnikową analizę wariancji (analiza wariancji klasyfikacji prostej). Metoda ta polega na analizowaniu wpływu pojedynczego czynnika posiadającego przynajmniej dwa poziomy (warianty) na wynik przeprowadzonego badania, czyli na obserwowaną zmienną tzw. zmienna zależną. Przykłady czynników: płeć, rodzaj pożywki lub diety, zastosowana kuracja. Hipotezy mają postać:

H₀: μ₁ = μ₂=……=μ_n

H : przynajmniej jedna średnia różni się od pozostałych

U podstaw omawianej techniki leży dokonanie podziału sumy kwadratów wariancji całkowitej (brane są pod uwagę wszystkie wartości pomiarów) na dwa składniki:

- wewnętrzną sumę kwadratów

- międzygrupowa sumę kwadratów

Pierwsza z nich opisuje zmienność wewnątrz grup, czyli odchylenia przypadkowe losowe. Druga - zmienność między grupami, czyli odchylenia wynikające z wpływu badanego czynnika. Chcąc uzyskać ogólne oszacowanie wariancji musimy podzielić sumę kwadratów wariancji całkowitej, czyli ogólną sumę kwadratów przez tzw. ogólną liczbę stopni swobody (N-1). Analogicznie aby uzyskać wewnątrzgrupowe oszacowanie wariancji dzielimy wewnątrzgrupową sumę kwadratów przez wewnątrzgrupowa sumę stopni swobody. W przypadku międzygrupowego szacowania wariancji wyliczamy iloraz międzygrupowej sumy kwadratów i międzygrupową sumę stopni swobody.

Całość podsumowuje tabela zwana tabela analizy wariancji:

Źródło zmienności	Suma kwadratów	df	Średnia kwadratów	F	P
Międzygrupowa	SSB	dfB (K-1)	SSB/dfBSB^2	S^2B/Sw^2
Wewnątrzgrupowa	SSW	dfW (N-K)	SSW/dfW Sw^2
Ogółem	SST	dfT (N-1)	SST/dfT

SS_T = SS_B + SS_W !!!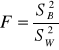
!!!!

df_T = df_B + df_W sygnał / szum

wzory niezbędne do wyliczenia SS podaje Łomnicki.

Jeżeli F ≤ 1 to stwierdzamy, że nie mamy podstaw do odrzucenia hipotezy zerowej. W przeciwnym razie sprawdzamy czy wyliczona na podstawie danych statystyka testowa znalazła się w obszarze krytycznym. Testując na poziomie istotności α posługujemy się tablicami dla wartości krytycznych na poziomie α. Wartości w główce wartości krytycznych odpowiadają międzygrupowej liczbie stopni swobody, zaś te w pierwszej kolumnie - wewnątrzgrupowej liczbie stopni swobody.

Test F jest testem dwustronnym korzystającym z jednego skrzydła rozkładu.

Są dwa modele jednoczynnikowej analizy wariancji (ANOVA) nieróżniące się obliczeniami, ale mogące się różnić interpretacją wyników. W modelu I czynnik różnicujący jest pod naszą kontrolą, a w modelu II czynnik różnicujący jest czynnikiem losowym, poza kontrolą.

Założenia jednoczynnikowej analizy wariancji:

- mierzalność zmiennej zależnej

- normalność rozkładu analizowanej zmiennej zależnej w każdej analizowanej populacji

- jednorodność wariancji rozważanego rozkładu

- addytywność - brak addytywności można rozpoznać po tym, że rozkład jest prawostronnie skośny

F = t²

(w przypadku testu t-Studenta dla prób niezależnych przy założeniu, że wariancje są takie same).

WYKŁAD 6 12.11.2008

Wieloczynnikowa analiza wariancji

Najprostszym jej rodzajem jest dwukierunkowa analiza zwana też analizą wariancji w klasyfikacji dwukierunkowej.

,

Gdzie: X_jk - wartość zmiennej zależnej, α_j - efekt główny j-tego poziomu czynnika A, β_k - efekt główny k-tego poziomu czynnika B, (αβ)_jk - efekt interakcji czynników

Wielką zaletą wieloczynnikowej analizy wariancji jest sposobność do oceny współdziałania - interakcji - braku niezależności pomiędzy czynnikami, co przekłada się na możliwość rozwiązywania bardziej złożonych problemów badawczych.

Interakcja - w przypadku klasyfikacji dwukierunkowej, oddziaływanie poziomu jednego z czynników na zmianę zależy od poziomu drugiego czynnika.

Mamy do czynienia z jedna skalą interwałową (zmienna zależna) i dwiema skalami nominalnymi (czynniki dzielące zmienną na grupy). Nominalnymi, gdyż poziomy każdego z czynników można ustawić w dowolnej kolejności nie zmieniając wyniku końcowego.

Mogące się pojawiać w etykietach poziomu liczby pełnią w tym momencie rolę opisowa pozwalającą rozróżnić te poziomy. Jeżeli oba czynniki, A i B, są kontrolowane przez badacza to mamy do czynienia z modelem I dwuczynnikowej analizy wariancji. Jeżeli oba zidentyfikowane i obserwowalne doświadczalnie czynniki mają charakter losowy - II model dwuczynnikowej analizy wariancji. W przypadku sytuacji pośredniej mamy do czynienia z modelem pośrednim - modelem mieszanym, tzw. modelem III dwuczynnikowej analizy wariancji.

Przykładem sytuacji w której powinniśmy rozważyć przeprowadzenie dwuczynnikowej analizy wariancji jest ta przedstawiona poniżej (zgodna z modelem I)

Dysponujemy pomiarami wapnia we krwi 8 ptaków pewnego gatunku (4 samców i 4 samic) przetrzymywanych w tych samych warunkach. Połowie ptaków przy zachowaniu stosunku płci na pewien czas przed pomiarem wstrzyknięto taką samą dawkę hormonu X.

Czynnik A (kuracja hormonalna)		Czynnik B (płeć)
		Zastosowano	samce	samice
				16,5 18,4	14,5 11,0
		Niezastosowano	39,1 26,2	33,0 23,8

Wykonując dwuczynnikową analizę wariancji dla danych z przykładu możemy przetestować 3 hipotezy zerowe:

1) H_o: podanie hormonu nie wpływa na średnie stężenie Ca we krwi, a więc brak wpływu czynnika A na zmienna zależną,

2) H_o: średnie stężenie Ca we krwi samców i samic nie różnią się, brak wpływu czynnika B na zmienna zależną,

3) H_o: nie występuje współdziałanie pomiędzy poziomami obu czynników, wpływ jednego z czynników na zmienną zależną jest taki sam przy wszystkich poziomach drugiego czynnika

Z tabeli można łatwo odczytać, że 8 pomiarów zostało rozsegregowane do 4 kombinacji poziomów obu czynników. Rzuca się też w oczy, że liczba pomiarów w każdej komórce jest taka sama. W takiej ze wszech miar pożądanej sytuacji mówimy o układzie zrównoważonym. Istotne jest też zwrócenie uwagi na fakt, że liczba pomiarów w każdej komórce jest większa od 1. Analiza wariancji przeprowadzona dla takiej sytuacji nosi nazwę dwuczynnikowej analizy wariancji z powtórzeniami (muszą być niezależne).

Wracając do mechaniki dwuczynnikowej analizy wariancji sumę kwadratów wariancji całkowitej możemy rozbić na kilka składników. Wewnątrzgrupową sumę kwadratów, czyli ocenę zmienności losowej, sumę kwadratów opisującą zmienność związaną z czynnikiem A, a więc między wierszami, sumę kwadratów związaną z czynnikiem B (sumę kwadratów między kolumnami), interakcyjną sumę kwadratów opisującą zmienność interakcji. Trzy ostatnie sumy kwadratów łącznie dają międzygrupową sumę kwadratów. Stopnie swobody oblicza się podobnie jak w jednoczynnikowej analizie wariancji traktując komórkę jako grupę. Interakcyjna liczba stopni swobody to międzykolumnowa liczba stopni swobody pomnożona przez międzywierszową liczbę stopni swobody.

Oszacowanie wariancji, czyli średnie kwadraty oblicza się w sposób podobny do jednoczynnikowej analizy wariancji, pomijając wariancję ogólną i między grupami.

Źródła zmienności	Suma kwadratów	Stopnie swobody	Oszacowanie wariancji	F	P
Ogólna	+	+	-	-	Różnie liczone
Międzygrupowa - wiersze (czynnik A) - kolumny (czynnik B) - interakcja	+	+	-	-
		+	+	+		+ (dla I, II, III modelu)
		+	+	+
		+	+	+
Wewnątrzgrupowa	+	+	+	-

Obliczanie wartości statystyki F różni się pomiędzy poszczególnymi modelami.

Źródło zmienności	F
		Model
		I	II	III
Wiersze
Kolumny
Interakcja

Niektórzy autorzy sugerują, aby w przypadku modelu II i III, gdy interakcja jest nieistotna statystycznie połączyć interakcję i wewnątrzgrupową sumę kwadratów i odpowiednie stopnie swobody, następnie obliczyć wspólne oszacowanie wariancji, które lepiej estymuje wariancje grupową i dalej testować istotność wpływu czynników na zmienną losową. Inni krytykują to podejście. Dobrze jest wyznawać zasadę, że poza pewnymi wyjątkami nigdy nie należy analizować efektów głównych gdy istnieje interakcja.

Wieloczynnikowa analiza wariancji nie ogranicza się tylko do klasyfikacji dwukierunkowej.

W sytuacji gdy mamy do czynienia z pomiarami powtarzalnymi, natomiast czynnik powtarzanych pomiarów ma powyżej dwóch poziomów stosujemy tzw. analizę wariancji z powtarzalnymi pomiarami. Jest to nic innego jak dwuczynnikowa analiza wariancji model III. Ponieważ w przypadku istnienia powyżej dwóch poziomów czynnika powtarzalności pomiarów nie jest możliwe używanie pojęcia „para wiązana” zastępuje się ja terminem „blok” będącym czynnikiem losowym. Standardowo mamy w takim przypadku do czynienia z analizą wariancji bez powtórzeń - analiza interakcji nie jest możliwa. Gdy nie mamy do czynienia z pomiarami powtarzalnymi, ale zasadne jest używanie bloków (patrz: Łomnicki 12.3), ten rodzaj analizy nazywa się analizą wariancji dla bloków całkowicie zrangowizowanych lub bloków losowych.

Przykład: Interesuje nas przyrost masy świnek morskich karmionych różnymi rodzajami karmy. Mamy 20 świnek. Czynnik stały - rodzaj diety - ma 4 poziomy i testujemy jego efekt. Czynnikiem losowym jest blok, do każdego bloku trafiają 4 świnki (bo mamy 4 diety). Przypisanie diety do każdego osobnika w ramach bloku jest losowe, ale przypisanie świnek do boksów już nie, bo badacz przypuszcza że trzeba razem grupować świnki przetrzymywane w klatkach stojących w określonym miejscu laboratorium, gdyż warunki otoczenia (np. bliskość wentylatora) mogą wpływać na przyrost masy. W niektórych eksperymentach może pojawić się kilka powtórzeń w ramach jednego zabiegu - możliwa jest analiza interakcji.

Do tej pory rozważaliśmy układ eksperymentu, w którym istniały wszystkie możliwe kombinacje poziomów czynników, czyli istniała klasyfikacja krzyżowa, ale zdarzają się przypadki, że klasyfikacja ma raczej naturę hierarchiczną, jej nazwa to hierarchiczna analiza wariancji. Dla dwóch czynników niektóre poziomy jednego z nich mogą być zagnieżdżone w jednym z poziomów drugiego czynnika, inne w innym poziomie drugiego czynnika. Czynnik zagnieżdżony jest zazwyczaj losowy, zaś czynnik wyższego rzędu stały. W eksperymentach hierarchicznych przyjmujemy założenie, że interakcje nie występują lub jest zaniedbywana. Przykładem hierarchiczności jest sytuacja, gdy dysponujemy wartościami zmiennej zależnej - np., poziom cholesterolu we krwi i 2 czynnikami - rodzaj leku i źródło pochodzenia. Każdy lek pochodzi z dwóch źródeł, ale nie jest taki sam dla wszystkich. Drugi czynnik jest zagnieżdżony w pierwszym.

Lek # 1	Lek # 2
Źródło A Źródło B	Źródło C Źródło D
……… ……….	………. ………..
……… ……….	………. ………..
……… ……….	………. ………..

Zazwyczaj hierarchiczną analizę wariancji stosuje się w celu uwzględnienia zmienności wewnątrzgrupowej podczas testowania efektów stałych, czyli czynników wyższego rzędu.

Wracając do jednoczynnikowej analizy wariancji - jeżeli dysponujemy zmienną zależną, którą czynnik różnicuje na kilka grup to możliwe jest po dokonaniu pewnego zabiegu przeprowadzenie jednoczynnikowej analizy wariancji, która będzie testem jednorodności wariancji dla dwóch lub większej liczby grup. Ów zabieg polega na zastąpieniu poszczególnych wartości danych przez wartości bezwzględne odchylenia od średniej dla grupy, z której pochodzą. Jest to tzw. test Levene'a. zamiast średniej możemy się posłużyć medianą.

WYKŁAD 7 19.11.2008

Aby sprawdzić czy losowo niezależna próba pochodzi z populacji generalnej o rozkładzie normalnym najlepiej jest użyć testu W. Shapiro-Wilka.

Podstawy korelacji i regresji

Skoncentrujemy się na metodach analizy związków pomiędzy dwoma zmiennymi. W przypadku badania zależności dwóch zmiennych losowych często używa się określenia szereg dwucyfrowy, gdyż w tym przypadku zamiast pojedynczych pomiarów dysponujemy ich parami. Badane jednostki charakteryzują dwie cechy - np. rozważając związek pomiędzy długością ciała i masą noworodka należałoby zmierzyć zarówno wzrost, jak i masę najmłodszych z losowo wybranej i jednakowo licznej grupy (należałoby sięgnąć do statystyk szpitalnych).

Zależność może przybierać dwie formy:

1. typu funkcyjnego - zakłada się, że zmiana wartości jednej zmiennej tzw. zmiennej niezależnej X powoduje zmianę wartości drugiej zmiennej tzw. niezależnej Y. Używa się też określeń zmienna objaśniająca i objaśniana. Jest to związek typu 1:1 (jeden do jeden), gdyż jednej wartości zmiennej objaśniającej odpowiada jedna wartość zmiennej objaśnianej.

2. Zależność probalistyczna (stochastyczna) - ogranicza się do analizy jej szczególnego przypadku zwanego zależnością korelacyjną (stochastyczną), czyli taką zależnością, której określonym wartościom zmiennej niezależnej odpowiadają średnie wartości zmiennej zależnej.

W statystyce mówiąc o korelacji dwóch zmiennych losowych najczęściej ma się na myśli zależność liniową. Ponieważ możliwe są zależności innego typu oraz brak zależności…….

Pierwszym krokiem do badania zależności korelacji powinno być wykonanie wykresu rozrzutu - prosty wykres obrazujący szereg dwucyfrowy na płaszczyźnie. Pary pomiarów traktowane są jako współrzędne punktu. Jeśli zależność ma kształt prostoliniowy, punkty będą się układać mniej więcej wzdłuż linii prostej przebiegającej pod pewnymi katami w stosunku do obu osi współrzędnych.

-

Ograniczymy się do zależności prostoliniowych.

Wzajemne powiązania przybierające formę zależności liniowej między dwiema zmiennymi losowymi charakteryzuje kowariancja:

Wygodny sposób:

Kowariancja zmiennej z nią samą jest równa jej wariancji. Dla zmiennych nieskorelowanych wynosi ona zero. Może przybierać wartości dodatnie i ujemne. Nie jest jednak wygodnym wskaźnikiem stopnia zależności zmiennych, gdyż nie ma ograniczeń co do zakresu przyjmowanych wartości. Natomiast jeśli ją wystandardyzujemy dzieląc przez iloczyn odchyleń standardowych otrzymamy współczynnik korelacji Pearsona, czyli liczbę oznaczaną r (R) jeśli jest estymatorem lub ζ jeśli jest parametrem. Wzór można uprościć do postaci:

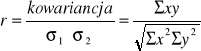
Przyjmuje on wartość z przedziału (-1, 1), gdy jest równy 0 to dwie zmienne losowe nie są skorelowane, gdy jest równy -1 lub 1 mówimy o korelacji całkowitej odpowiednio ujemnej lub dodatniej, to r a w zasadzie jego wartość bezwzględna (
) określa siłę związku rozumianego jako zależność liniowa dwóch zmiennych mierzalnych, natomiast znak „+”, „-” kierunek zależności. W przypadku gdy
=1 zależność korelacyjna przechodzi w zależność funkcyjną, tzn. wszystkie punkty leżą dokładnie na linii prostej. Pamiętajmy, że nie zawsze istnieje związek przyczynowo-skutkowy pomiędzy dwiema zmiennymi skorelowanymi, nawet silnie. Ponadto analiza korelacji nie wyróżnia żadnej z dwóch zmiennych, wręcz nie należy ich określać jako zmienna niezależna i zależna, zaś zależność najlepiej rozumieć jako współzależność.

Współczynnik korelacji i kowariancji będą takie same bez względu którą zmienną oznaczymy jako X, a którą jako Y. aby móc przetestować istotność współczynnika korelacji musimy założyć, że obie zmienne maja rozkłady zgodne z rozkładem normalnym (tzw. dwuwymiarowy rozkład normalny). Nawet Bardzo słaba korelacja może być istotna statystycznie, a wysoka - niekoniecznie. Hipoteza zerowa testu t głosi H₀: ζ=0, czyli korelacja nie jest istotna.

Jeśli naszym celem jest poznanie kształtu zależności pomiędzy dwiema mierzalnymi zmiennymi losowymi wkraczamy na obszar tzw analizy regresji. Ograniczymy się do zależności liniowej. Stosując techniki analizy regresji będziemy dopasowywali linie prosta do danych empirycznych.

Prosta Y= a + bX charakteryzuje się określonym nachyleniem do osi OX. Współczynnik nachylenia to „b”, punkt przecięcia z OY to „a”. Nie byłoby problemu gdyby wszystkie punkty leżały na linii prostej. W praktyce badawczej z taką sytuacją się nie spotykamy. W związku z tym musimy poszukać równania takiej prostej, która będzie najlepiej dopasowana do naszych danych. Można tego dokonać na kilka sposobów, zależnie od potrzeby i charakteru zmiennej. Omówione będą dwie metody. Dysponując próbami z populacji jedyne co możemy zrobić to estymować parametry. Nasze „a” estymuje parametr „α”, „b” parametr „β”. Jeśli obie zmienne charakteryzują się dwuwymiarowym rozkładem normalnym, zaś pomiary obu zmiennych różnią się rzędem wielkości lub skalą (np. gram i cm) najlepiej posłużyć się osią główną zredukowaną RMA (oprócz RMA jest też oś główna). W tym przypadku mówimy o modelu II szeregu dwucechowego, czyli o modelu II regresji, np. powierzchnia liści w zależności od ich długości. Przypisanie określeń zmienna niezależna i zależna jest całkowicie arbitralne. W tym podejściu najlepiej dopasowana prosta to taka dla której suma pól powierzchni trójkątów, z których każdy jest utworzony przez prostą oraz dwa odcinki (równoległe do osi OX i OY) łączące prostą i dany punkt jest najmniejsza. Zwróćmy uwagę na fakt, że brane są pod uwagę obu pomiarów X i Y od osi głównej.

-

Oś ta przebiega zawsze przez punkt wyznaczony przez średnie X i Y. Współczynniki „a” i „b” wylicza się na podstawie wzorów: Y= a + bX

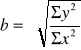
o znaku „±”decyduje znak
.

Istnieje tez model I regresji, o którym mówimy w sytuacji, gdy jedna ze zmiennych, czyli zmienna niezależna nie jest zmienną losową o rozkładzie normalnym, ale jest kontrolowana przez badacza.

Przykład: przyrost masy ciała prosiąt w zależności od ilości dostarczanego codziennie pokarmu. Zmienna zależna dla danej wartości zmiennej niezależnej powinna mieć rozkład normalny, jednorodność wariancji powinna być zachowana.

W modelu I do danych empirycznych dopasowujemy prostą regresji. Posługujemy się metoda najmniejszych kwadratów. Najlepiej dopasowana prosta to taka dla której suma kwadratów odchyleń pomiarów wartości zmiennej zależnej od tej prostej jest najmniejsza. Jest to regresja Y po X, a wiec interesująca nas zależność jest jednokierunkowa. Można to przedstawić graficznie:

-

Prosta regresji podobnie jak oś główna zredukowana przechodzi przez punkt wyznaczony przez średnie X-ów i Y-ków,, współczynniki prostej wyznaczamy w oparciu o wzory:

Y= a + bX

Współczynnik nachylenia (b) określa o ile jednostek przeciętnie zmieni się (wzrośnie lub zmaleje) wartość zmiennej zależnej przy wzroście zmiennej niezależnej o 1 jednostkę. Pomiędzy współczynnikiem liniowym Pearsona i współczynnikiem nachylenia prostej regresji zachodzi następujący związek:

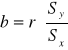
, gdzie S_x- odchylenie standardowe Xów, S_y- odchylenie standardowe Yków.

Jeśli związek między zmienną niezależną i zależną nie istnieje to b będzie zbliżone do zera. Nie można tego powiedzieć współczynniku nachylenia osi głównej zredukowanej. Jeśli r jest istotnie różne od zera, co można zbadać odpowiednim testem t, to „b” z modelu I tez takie będzie. Jedyny test jaki można wykonać w modelu II to test istotności współczynnika korelacji. Istotność współczynnika korelacji i nachylenia prostej regresji można także testować przy pomocy jednoczynnikowej analizy wariancji (szczegóły w Łomnickim).

Błąd standardowy estymacji (SEE) jest to zgrubna miara błędu estymacji……..

Jeśli podniesiemy do kwadratu r to otrzymamy współczynnik determinacji R². ten współczynnik stanowi opisową miarę dokładności dopasowania regresji do danych empirycznych. Może być podany w dwóch skalach albo jako wartość od 0 do 1, albo w procentach. Mówi on o tym, jaka część obserwowanej na postawie próby całkowitej zmienności zmienna zależna jest wyjaśniona przez zmienną niezależną. Im R² większe tym lepiej. W zależności od charakteru danych kształt zależności między zmiennymi opisuje bądź prosta regresji, os główna lub oś główna zredukowana. Prosta regresji może być także wykorzystywana do celów predykcji spodziewanej wartości zmiennej zależnej dla danego poziomu zmiennej niezależnej. Ta metoda jest sugerowana w przypadku danych odpowiadających modelowi II. Dobrym zwyczajem jest zastosowanie obu metod, prostej regresji i osi głównej zredukowanej, i porównanie wyników. Problem z osią główną zredukowaną w przypadku predykcji jest niemożność oszacowania błędu tej predykcji.

Analiza regresji:

	Model I	Model II
Kształt zależności prostoliniowej	Prosta regresji	Oś główna lub oś główna zredukowana RMA
Możliwe testy istotności	Test istotności współczynnika a, test istotności współczynnika b	Tylko test istotności współczynnika korelacji r (test t)
Predykcja	W oparciu o prostą regresji	Też w oparciu o prostą regresji, a najlepiej w oparciu o prostą regresji i oś główną zredukowaną RMA i porównanie wyników

Jeśli interesuje nas zależność między mierzalną zmienną zależną i więcej niż jedna zmienną niezależną wkraczamy na obszar regresji wielokrotnej.

---