WMS	Imię i nazwisko: Bożena Skrzypek Tomasz Sumara			Zespół: 3	Grupa: Środa 14.45	Rok III
Nr ćwiczenia: 11	Temat: Moduł Younga
Data wykonania: 21.10.09	Data oddania: 28.10.09	Zwrot do poprawy: 04.11.09	Data oddania: 18.11.09		Data zaliczenia:	Ocena:

1. CEL ĆWICZENIA:

Wyznaczenie modułu Younga metodą statyczną za pomocą pomiaru wydłużenia drutu z badanego materiału obciążonego stałą siłą.

2. WPROWADZENIE:

Odkształcenie ciała stałego pod wpływem sił zewnętrznych polega na przemieszczaniu się cząsteczek (atomów) tego ciała względem siebie z pierwotnego położenia równowagi w inne. Przemieszczeniu temu przeciwdziałają siły wewnętrzne ciała pochodzące od wzajemnego oddziaływania między cząsteczkami (atomami). Odkształcenie nazywa się sprężystym, jeśli ciało po ustaniu działania sił wraca do swego stanu początkowego. Po przekroczeniu granicy sprężystości ustanie działania siły zewnętrznej nie powoduje powrotu do pierwotnego kształtu, a odkształcenie jest trwałe (plastyczne). Siła odkształcająca powoduje zmianę odległości między cząsteczkami, której przeciwdziałają siły międzycząsteczkowe, które w tym przypadku są siłami sprężystości. Są one równe co do wartości, ale przeciwnie skierowane do sił odkształcających.

Siła sprężystości jest dana zależnością:

znaną jako prawo Hooke'a. Stała k nazywana stałą sprężystości jest miarą sztywności sprężyny. Im większa wartość k, tym sprężyna jest sztywniejsza.

Naprężenie normalne jest to stosunek siły normalnej, do pola przekroju o kierunku i zwrocie zgodnym z kierunkiem i zwrotem wektora siły:

Dla małych odkształceń możemy sformułować prawo Hooke'a w następującej postaci:

Czyli jeśli działające na ciało naprężenia zewnętrzne są dostatecznie małe, to wywołane przez nie odkształcenia są do nich wprost proporcjonalne,

Prawo to dla jednostronnego rozciągania (ściskania) ma wartość:

gdzie E - moduł Younga (stosunek naprężenia normalnego do względnego wydłużenia, wyrażany w
)

Uwzględniając zależność liniową
od F (a=
):

Sprężyny można łączyć ze sobą równolegle lub szeregowo. Wypadkowy

współczynnik sprężystości k połączonych sprężyn jest zdefiniowany zależnością:

gdzie F i x oznaczają siłę przyłożoną do układu sprężyn i jego wydłużenie.

Dla połączenia równoległego dwóch sprężyn o współczynnikach sprężystości odpowiednio

k₁ i k₂ działająca na nie siła jest sumą sił F₁ i F₂ działających na poszczególne

sprężyn, a ich wydłużenia są jednakowe. Zachodzą wiec zależności:

F₁ = k₁x, F₂ = k₂x

F = F₁ + F₂

z których otrzymuje się związek:

k = k₁ + k₂

Dla szeregowego połączenia sprężyn działające na nie siły są, przy pominięciu ciężaru sprężyn jednakowe, natomiast ich łączne wydłużenie jest sumą wydłużeń x₁ i x₂ obu sprężyn. Mamy wiec zależności:

F = k₁ x₁ , F = k₂ x₂

x = x₁₊ x₂

z których wynika związek:

Dźwignia dwustronna - maszyna prosta, w której siły działają po przeciwnych stronach osi obrotu. Dźwignia pozostaje w równowadze, gdy wypadkowy moment przyłożonych do niej sił wynosi 0.

Krążek przesuwny - krążek podparty swobodnie, przez który przeplata się cięgno. W trakcie przesuwania się cięgna obtacza się po nim z założenia bez poślizgu. Umożliwia to zmianę wartości siły.

Regresja w ogólności to problem estymacji warunkowej wartości oczekiwanej. Regresja liniowa jest nazywana liniową, gdyż zakładanym modelem zależności między zmiennymi zależnymi, a niezależnymi, jest funkcja liniowa. Dla jednej zmiennej zależnej zagadnienie polega na poprowadzeniu prostej y=ax+b jak najlepiej dopasowanej do zbioru n punktów doświadczalnych. Celem dopasowania jest przede wszystkim uzyskanie ocen wartości parametrów a i b opisujących prostą, oraz ich niepewności u(a) i u(b).

3. UKŁAD POMIAROWY:

Statyw do pomiaru z przymocowanym na stałe czujnikiem zegarowym, odważniki,

śruba mikrometryczna, przymiar liniowy.

4. OPIS ĆWICZENIA:

1. Pomiar długości drutu mosiężnego przymiarem przymocowanym do ramienia statywu.

2. Zamocowanie drutu w statywie.

3. Po obciążeniu szalki czterema odważnikami kilogramowymi, pomiar średnicy drutu w 10 różnych miejscach równomiernie rozłożonych na całej długości za pomocą śruby mikrometrycznej.

4. Po wyzerowaniu czujnika mikrometrycznego, zmieniając masę o 1kg w granicach 0-10kg, pomiar dla rosnących oraz malejących wartości ciężaru.

5. Analogiczne pomiary dla drutu stalowego.

5. WYNIKI POMIARÓW:

Długość drutu: l = 1069(1) [mm]

Wartość średnia średnicy:

[

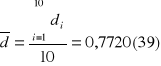
Niepewność standardowa została obliczona następująco:

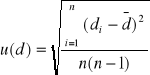
=0,0039 [mm]

Zwiększając obciążenie o 1kg, a następnie zmniejszając odczytaliśmy pomiar czujnika mikrometrycznego, a następnie podzieliliśmy otrzymane wartości przez 2, aby otrzymać wydłużenie drutu (z uwagi na to, iż w doświadczeniu korzystaliśmy z dźwigni).

Wyniki zamieściliśmy w tabeli.

Przyjmując
, obliczamy pole przekroju:

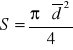
u(S)=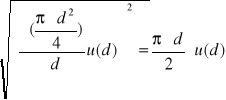

dla drutu mosiężnego

[mm²] = 4,681
[m²]

u(S)=

dla drutu stalowego:

=

[m²]

u(S)=

Oraz przyjmując g
[
], obliczamy siłę F:

[N]

Za pomocą komputera w pracowni znaleźliśmy współczynnik regresji liniowej dla drutu mosiężnego:

l=
, więc:

[a]=

a=0,025669(0,000076) [
]=2,5669 (76)
[

u(a)= 0,000076[
]

Analogicznie znaleźliśmy współczynnik regresji liniowej dla drutu stalowego:

a=0,01206(
) [
]=1,206 (12)
[

u(a)= 0,00012056 [
]
[
]

Wykresy zależności wydłużenia od siły dla obu drutów, wykonane w pracowni laboratoryjnej, dołączamy na końcu sprawozdania.

Do wyznaczenia współczynników posłużyliśmy się też metodą graficzną.

Drut mosiężny		Drut stalowy
x (siła [N])	y (wydłużenie [mm])	x (siła [N])	y (wydłużenie [mm])
9,81	0,28	9,81	0,175
19,62	0,53	19,62	0,315
29,43	0,775	29,43	0,44
39,24	1,045	39,24	0,56
49,05	1,29	49,05	0,675
58,86	1,54	58,86	0,795
68,67	1,8	68,67	0,915
78,48	2,05	78,48	1,025
88,29	2,29	88,29	1,135
98,1	2,54	98,1	1,25

Współczynnik a obliczamy jako tangens kąta nachylenia wyznaczonej przez nas prostej.

a =

Dla drutu mosiężnego:

Dla drutu stalowego:

6. OBLICZENIE MODUŁU YOUNGA

Korzystając ze wzoru obliczamy moduł Younga dla mosiądzu:

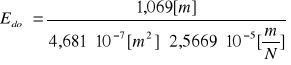
88,967239 [GPa]

Odczytujemy wartość tablicową modułu Younga dla mosiądzu:

E_tabl=100 [GPa]

Obliczamy podobnie moduł Younga dla stali:

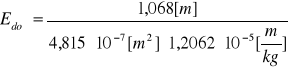
183,88951 [GPa]

Odczytujemy wartość tablicową modułu Younga dla żelaza:

E_tabl=210
220 [GPa]

Następnie obliczamy niepewność pomiaru modułu Younga, korzystając ze wzoru na niepewność złożoną:

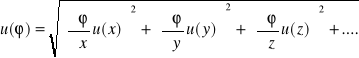
Dla drutu mosiężnego:

u(E)=[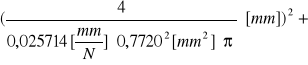

+(
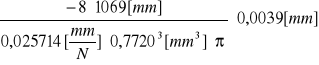
)² +

+

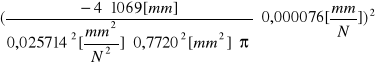
[Pa] = 0,94 [GPa]

Dla drutu stalowego:

u(E) = [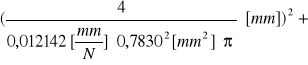
+(
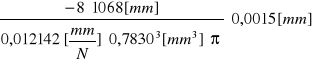
)² + +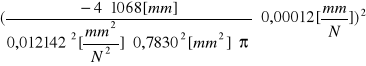

u(E) = 1,97583

Sprawdzamy czy zadanie zostało wykonane poprawnie, wstawiając do wzoru:

Dla drutu mosiężnego:

Dla drutu stalowego:

Tabele podsumowujące:

^Rodzaj materiału: mosiądz					^Długość drutu: 1069 [mm]
^średnica [mm]	^0,77	^0,78	^0,79	^0,78	^0,79	^0,76	^0,77		^0,76	^0,76	^0,76
^średnia średnica ^d=0,7720[mm]			^u(d)=0,0039^[mm]		^Pole przekroju S =				u(S) =
^Masa odważników [kg]	^1	^2	^3	^4	^5	^6	^7		^8	^9	^10
^Siła [N]	^9,81	^19,62	^29,43	^39,24	^49,05	^58,86	^68,67		^78,48	^88,29	^98,1
^wydłużenie F	^0,26	^0,50	^0,74	^1,01	^1,25	^1,51	^1,77		^2,02	^2,28	^2,54
wydłużenie F	^0,30	^0,56	^0,81	^1,08	^1,33	^1,57	^1,83		^2,08	^2,30	^2,54
^wydłużenie	^0,28	^0,53	^0,765	^1,045	^1,29	^1,54	^1,80		^2,05	^2,29	^2,54
^a (z dopasowania graficznego)^=				^E=^88,81 [GPa]
^a (z prostej regresji)^= 0,025669[ ]				E = 88,97 [GPa]				u(E) = 0,94 [GPa]
								^Etabl=100[GPa]

^Rodzaj materiału:^stal					^Długość drutu: 106^8^[mm]
^średnica [mm]	^0,78	^0,78	^0,79	^0,78	^0,78	^0,78	^0,79		^0,79	^0,78	^0,78
^średnia średnica ^d=0,7^830^[mm]			^u(d)=0,00^15[mm]		^Pole przekroju S =				u(S) =
^Masa odważników [kg]	^1	^2	^3	^4	^5	^6	^7		^8	^9	^10
^Siła [N]	^9,81	^19,62	^29,43	^39,24	^49,05	^58,86	^68,67		^78,48	^88,29	^98,1
^wydłużenie F	^0,17	^0,31	^0,43	^0,55	^0,67	^0,78	^0,91		^1,02	^1,13	^1,25
wydłużenie F	^0,18	^0,32	^0,45	^0,57	^0,68	^0,81	^0,92		^1,03	^1,14	^1,25
^wydłużenie	^0,175	^0,315	^0,44	^0,56	^0,675	^0,795	^0,915		^1,025	^1,135	^1,25
^a (z dopasowania graficznego)^=				^E=^182,68 [GPa]
^a (z prostej regresji)^= 0,01206[ ]				E = 184 [GPa]				^u(E)=^2,0[GPa]
								^Etabl=210 [GPa]

7. WNIOSKI

Wykres zależności przyrostu długości od działającej siły w całym badanym zakresie zmian jest zależnością liniową (przy obu drutach: żelaznym i mosiężnym), co świadczy o tym, że podczas pomiarów nie została przekroczona granica sprężystości.

Błąd pomiaru jest duży (wynik nie zgadza się w granicach niepewności pomiaru z wartością tablicową), co świadczy o niedoskonałości metody pomiarowej, a także złym stanie początkowym drutów, na których przeprowadzane było doświadczenie.

Strona 9 z 9

---