POLITECHNIKA LUBELSKA W LUBLINIE		LABORATORIUM ELEKTROTECNIKI Ćwiczenie Nr 13
Nazwisko: Kukawski Jabłoński Zinkiewicz Malec	Imię: Mikołaj Adam Wojciech Łukasz	Semestr III	Grupa E.D.3.3	Rok akadem. 2002/2003
Temat ćwiczenia: Synteza dwójników pasywnych			Data wykonania 17.12.2002 r	Ocena:

Rys. Układ do badania charakterystyk amplitudowych i fazowych dwójnika pasywnego.

1. WIADOMOŚCI WSTĘPNE.

1. Wstęp.

Problem syntezy dwójnika liniowego pasywnego polega na wyznaczeniu modelu strukturalnego, łącznie z wartościami elementów, odpowiadającego zadanej funkcji F(s). O ile w zagadnieniu analizy danemu dwójnikowi można przyporządkować tylko jedną funkcję immitancji Z(s) lub Y(s), to w zagadnieniu syntezy danej funkcji immitancji odpowiada szereg różnych modeli.

Aby dana funkcja F(s) mogła być realizowana w sensie modelu fizycznego, musi być ona funkcją wymierną rzeczywistą dodatnią. Niech funkcja F(s), zwana też immitancją lub funkcją przejścia, dana będzie w postaci ilorazu dwóch funkcji rzeczywistych wymiernych o współczynnikach a_k i b_k dodatnich:

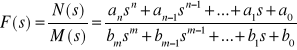
Funkcja ta jest wymierną rzeczywistą dodatnią i może być realizowana przez model fizyczny gdy spełnia następujące warunki:

1. Wszystkie współczynniki wielomianów są rzeczywiste i dodatnie;

2. Bieguny i zera leżą w lewej półpłaszczyźnie lub osi urojonej a residua w tych biegunach są dodatnie;

3. Bieguny i zera leżące na osi urojonej są pojedyncze łącznie z punktem s=∞, a residua w tych biegunach są dodatnie;

4. Stopień licznika i mianownika różnią się co najwyżej o jeden;

5. Część rzeczywista na osi urojonej spełnia warunek Re F(jω)≥0.

Warunki te nie uwzględniają możliwości technicznych realizowania układów RLC ze względu na ograniczoną wartość tych elementów.

Jest szereg metod pozwalających na realizację funkcji F(s) spełniających warunki funkcji wymiernej rzeczywistej dodatniej. Wszystkie metody polegają na rozkładzie wielomianów określających daną funkcję i z jego postaci wyciągnięcia wniosków o strukturze odpowiadającego jej modelu.

W przypadku syntezy dwójników liniowych pasywnych istnieją dwie podstawowe metody syntezy:

1. metoda Fostera, polegająca na kolejnym wydzielaniu biegunów i zer oraz rozkładzie danej immitancji na ułamki proste i przyporządkowaniu tym ułamkom elementarnych obwodów RL, RC, LC oraz RLC;

2. metoda Cauera, bazująca na rozwinięciu zadanej immitancji w ułamek łańcuchowy i w konsekwencji przyporządkowaniu mu układu drabinkowego elementów.

Metody te nazywamy kanonicznymi.

2. Metoda Fostera:

Mając dane bieguny immitancji rozkładamy Z(s) na ułamki proste i poszczególnym składnikom otrzymanej sumy przyporządkowujemy odpowiednie elementy R, L, C lub ich połączenia:

Impedancja połączenia z rysunku powyżej ma postać:

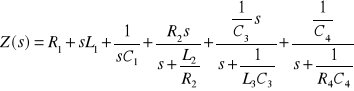
co odpowiada ogólnej postaci wyrażenia :

.

Z porównania współczynników stojących przy odpowiadających sobie wyrazach zależności 1 i 2 można obliczyć wartości elementów R, L, C. A zatem, głównym problemem w syntezie metodą Fostera staje się znalezienie biegunów immitancji i jej rozkład na ułamki proste. Współczynniki k występujące w tym rozkładzie obliczamy korzystając z metody residuów:

- odpowiadający indukcyjności L=k_∞;

- odpowiadający pojemności
;

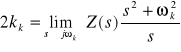
- odpowiadający indukcyjności i pojemności;

- odpowiadający obwodowi RL;

- odpowiadający obwodowi RC.

W przypadku syntezy immitancji Z(s) wydziela się kolejno bieguny w nieskończoności i zerze (jeśli istnieją), a następnie od funkcji Z(s) odejmie się wydzieloną funkcję Z₁(s):

Z(s)-Z₁(s)=Z¹(s)

Otrzymuje nową funkcję Z¹(s) o obniżonym stopniu. Po wyodrębnieniu Z₁(s), poszukuje się nadal biegunów i zer funkcji Z¹(s). Jeżeli znamy zero tej nowej funkcji, to wygodniej jest realizować nie Z₂(s) lecz
, dla której zera impedancji są bieguna

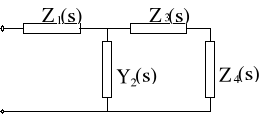
mi. Wyodrębniamy bieguny admitancji Y¹(s), a w schemacie Fostera dochodzi gałąź poprzeczna złożona z odpowiadających im elementów. Obniżając w ten sposób każdorazowo stopień wielomianu dochodzimy do wyrażenia, które odpowiada bezpośrednio jednemu ze znanych połączeń RL, RC lub LC. Przykładowo, na rysunku 2 przedstawiono schemat realizujący zadaną funkcję Z(s), w której wydzielono Z₁(s), Y₂(s), Z₃(s) oraz Z₄(s).

3. Metoda Cauera.

Metoda polega na realizacji zadanej funkcji Z(s) lub Y(s) przez układ drabinkowy, którego elementy uzyskujemy z dzielenia wielomianów określających Z(s) metodą ułamka łańcuchowego.

Układ z rysunku 3 można opisać ułamkiem łańcuchowym o postaci :

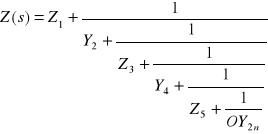
Metoda ta wydaje się być bardzo dobra, gdyż unikamy tu podstawowej trudności metody Fostera, tj. wyszukiwania biegunów i zer immitancji. Tak jest w istocie, ale tylko w przypadku, gdy impedancje Z i admitancje Y występujące w ułamku łańcuchowym przedstawionym powyżej i przedstawiają sobą idealne elementy R, L lub C. Jeżeli impedancje Z_2n-1 i Y_2n przedstawiają elementy PL., RC lub LC to przedstawienie Z(s) przez układ drabinkowy metodą Cauera wymaga wielokrotnych prób.

II. WYKONANIE ĆWICZENIA.

1. Dla zadanej immitancji Z(s) dokonano syntezy dwójnika w oparciu o elementy pasywne R, L, C stosując metodę Cauera i Fostera z wykorzystaniem programu komputerowego Synteza.Exe. Wyniki obliczeń w postaci charakterystyk amplitudowych i fazowych zamieszczono na dołączonym wydruku z programu.

2. Zbudowano zadany dwójnik i wyznaczono charakterystyki amplitudowe i fazowe Z(jω)=f₁(ω) argZ(jω)=f₂(ω) przy stałej amplitudzie napięcia zasilającego i zmiennej częstotliwości f. Charakterystyki wyznaczono w układzie pomiarowym z rysunku 4.

Wyniki pomiarów zamieszczono w tablicy 1.

Lp	f	U	I	φ	|z|	φteoret	|z|
-	[Hz]	[V]	[A]	-	[Ω]	-	[Ω]
1	50	10	0,1	50,734	95,46	1,559	126,5
2	70	10	0,145	1,38	43,17	1,561	121,3
3	90	10	0,185	1,24	30,28	1,562	110,3
4	100	10	0,21	1,25	24,9	1,566	100
5	150	10	0,34	0,98	22,11	1,567	91,57
6	200	10	0,4	0,85	20,46	1,568	83,3
7	250	10	0,42	0,74	19,39	1,568	81,25
8	300	10	0,41	0,67	18,62	1,569	76,92
9	350	10	0,38	0,58	18,05	1,569	70,94
10	400	10	0,35	0,49	17,59	1,569	66,66
11	600	10	0,24	0,42	17,21	1,569	60,6
12	800	10	0,185	0,34	16,87	1,569	58,13

Wyniki obliczeń w postaci charakterystyki amplitudowej i fazowej:

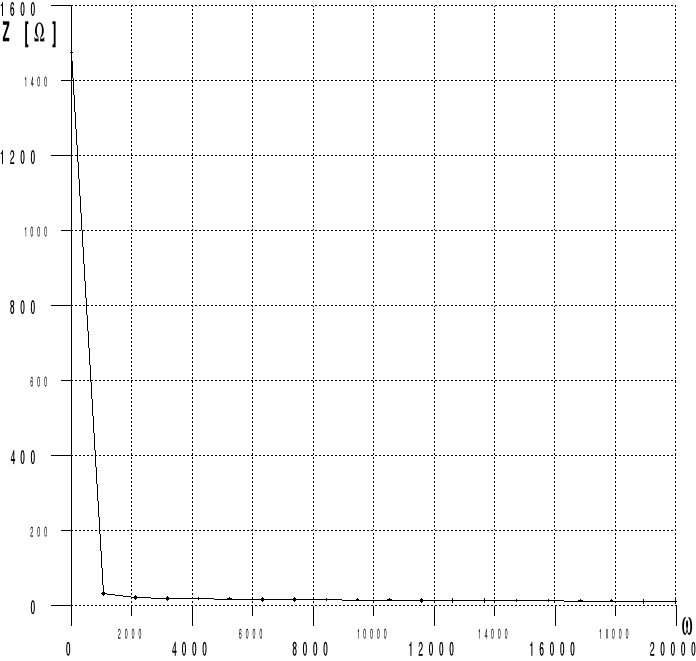
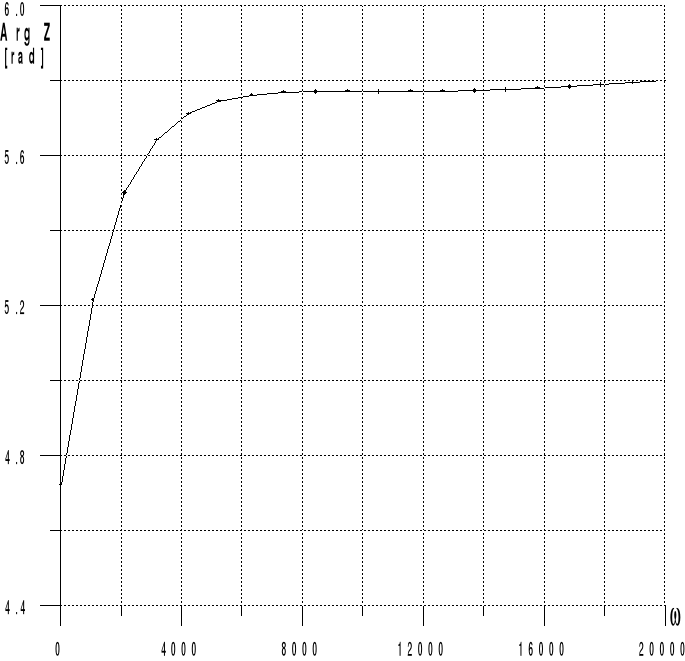
W oparciu o dane elementy: R₁=7,5  R₂=8,2  C₁=33,7 F C₂=10 F L=0,45 H

stosując metodę Fostera z wykorzystaniem programu komputerowego otrzymujemy charakterystyki odpowiednio amplitudową i fazową:

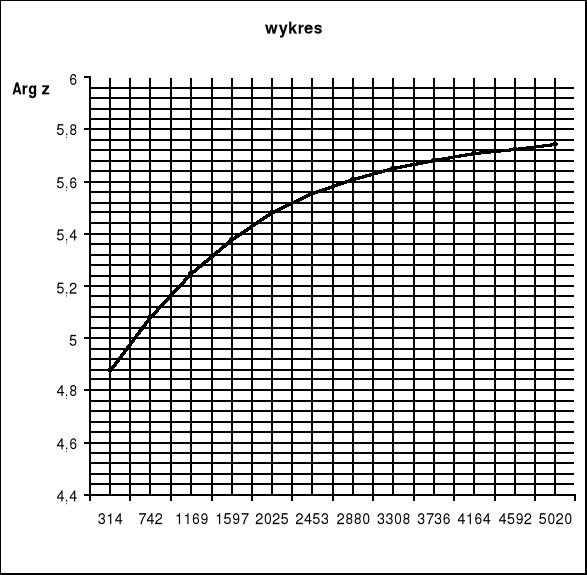
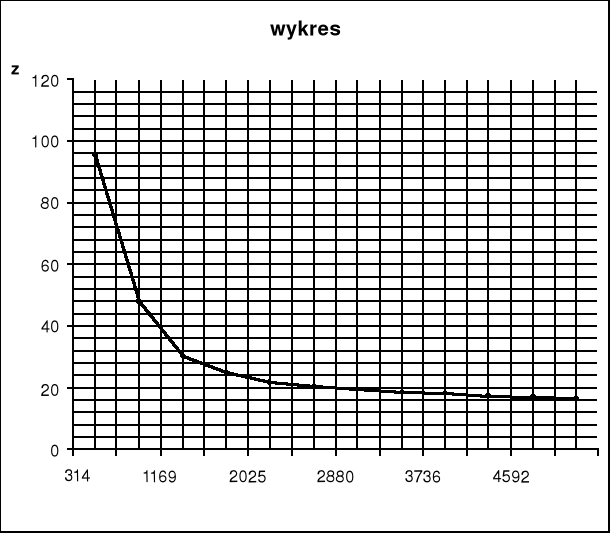
Wnioski i spostrzeżenia:

Znaczne różnice między amplitudami impedancji obliczonymi teoretycznie (za pomocą programów liczących), a wyznaczonymi z pomiarów wynikają przede wszystkim z niedokładności odczytu z przyrządów pomiarowych (m.in. dlatego, że watomierz był przystosowany do pomiarów w zakresie częstotliwości 20-200 Hz, a także błąd odczytu wynikający z małych wartości mocy w obwodzie do których nie był przystosowany W).

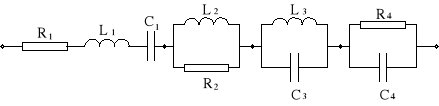
Rysunek 1 Przykład realizacji impedancji Z(s)

Rysunek 2 Schemat realizujący zadaną funkcję

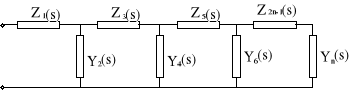
Rysunek 3 Układ drabinkowy realizacji immitancji metodą Cauera

---