POLITECHNIKA WARSZAWSKA

Laboratorium z przedmiotu: PODSTAWY TECHNIKI POMIAROWEJ Ćwiczenie nr 4. Temat : Wyznaczanie charakterystyk zmiennych losowych na podstawie danych eksperymentalnych . Grupa LTS-2 sem VI Zespół nr 3 : 1. KRUK TOMASZ 2. CHMIELEWSKI GRZEGORZ 3. BORKOWSKI MICHAŁ 4. ŁUKASZ DĘBSKI

CEL ĆWICZENIA

Zapoznanie się z podstawowymi metodami statystycznej oceny wyników pomiarów otrzymanych na stanowisku kontroli produkcji.

1. OPIS TEORETYCZNY

Uzyskany w wyniku pomiarów ciąg n - elementowy wartości pewnej wielkości x, utożsamiamy ze zmienną losową. Wartości (x₁, x₂, ..., x_n) zmiennej losowej x nazywamy próbą n - elementową. Zadaniem opracowującego wyniki pomiarów eksperymentalnych jest znalezienie ocen (wartości przybliżonych) dla charakterystyk liczbowych danej zmiennej losowej.

Charakterystykami tymi są :

• wartość średnia (oczekiwana) E(x),

• odchylenie standardowe
  ,

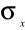
• wariancja D²(x),

• momenty wyższych rzędów
  ,
  ,

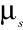
• współczynnik asymetrii i spłaszczenia
  ,
  .

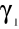
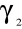
Oceny tych charakterystyk, uzyskane na podstawie wyników badań

Eksperymentalnych, oznaczamy tymi samymi literami, co szukane charakterystyki, lecz z „wężykiem” u góry
,
, itp. Przy nieograniczonym wzroście liczebności próby n ocena powinna być zbieżna wg prawdopodobieństwa do ocenianego parametru.

Ocenę nazywamy nieobciążoną, jeśli przy dowolnej liczebności próby jej wartość oczekiwana pokrywa się z szukanym parametrem.

Średnia arytmetyczna z wyników n doświadczeń :

gdzie :

c - dowolna liczba (pozorne zero) jest oceną nieobciążonej wartości oczekiwanej.

Oceną nieobciążoną odchylenia standardowego jest :

,

gdzie :

- współczynnik będący funkcją n.

Mając liczną próbę, elementy próby łączymy, grupujemy w klasach, tworząc tzw. uporządkowany szereg rozdzielczy (x⁰, x¹)(x¹, x²), ...,(x^k-1,x^k). Oceny wartości oczekiwanej, wariancji i momentów wyższych rzędów dokonuje się wtedy w sposób przybliżony, korzystając ze wzorów :

,

gdzie :

- wartość średnia w j-tej klasie,

- częstość (prawdopodobieństwo) zdarzenia w j-tej klasie.

Korzystając z danych uzyskanych przy tworzeniu uporządkowanego szeregu rozdzielczego, wykonujemy histogram, czyli zależność
, oraz dystrybuantę empiryczną
.

2. OPIS STANOWISKA POMIAROWEGO
   

Za pomocą czujnika indukcyjno - analogowego Vistronik A, dla wskazanego przez prowadzącego ćwiczenie, zbioru detali dokonaliśmy pomiaru odchyłek wymiaru podlegającego kontroli.

Wyniki pomiarów odchyłki przedstawia poniższa tabela:

Lp.	odchyłka	wymiar detalu [mm]	Lp.	Odchyłka [μm]	wymiar detalu [mm]
						[μm]
1	+60	15,060	31	-60	14,940
2	+40	15,040	32	-80	14,920
3	+20	15,020	33	-60	14,940
4	0	15,000	34	+40	15,040
5	-140	14,860	35	-100	14,900
6	+20	15,020	36	0	15,000
7	+40	15,040	37	+20	15,020
8	0	15,000	38	-200	14,800
9	-200	14,800	39	-120	14,880
10	+20	15,020	40	+60	15,060
11	+40	15,040	41	+160	15,160
12	+60	15,060	42	+120	15,120
13	-160	14,840	43	-200	14,800
14	-200	14,800	44	+20	15,020
15	+20	15,020	45	-20	14,980
16	-60	14,940	46	-140	14,860
17	0	15,000	47	-100	14,900
18	+400	15,400	48	-120	14,880
19	+40	15,040	49	+320	15,320
20	-40	14,960	50	+120	15,120
21	+120	15,120	51	-220	14,780
22	+20	15,020	52	+200	15,200
23	0	15,000	53	-20	14,980
24	-40	14,960	54	+60	15,060
25	-100	14,900	55	+160	15,160
26	0	15,000
27	+140	15,140
28	-180	14,820
29	+180	15,180
30	+80	15,080

Wartość nominalna wymiaru 15 mm.

Ustaliliśmy wartości minimalną i maksymalną pomiarów, które wynoszą:

• min. -220 µm

• max. +400 µm

3. PRZYKŁADOWE WYLICZENIA
   

Tworzenie uporządkowanego szeregu rozdzielczego.

Otrzymane wyniki pomiarów pogrupowaliśmy w 8 klas i dokonaliśmy obliczeń częstości klasy, oraz dystrybuanty empirycznej

Nr klasy (grupy)	1	2	3	4	5	6	7	8	9	10
Granica klasy	14,800	14,860	14,920	14,980	15,040	15,100	15,160	15,220	15,280	15340
		14,860	14,920	14,980	15,040	15,100	15,160	15,220	15,280	15,340	15,400
Wartość średnia klasy	14,830	14,890	14,950	15,010	15,070	15,130	15,190	15,250	15,310	15,370
Liczba elementów w klasie mj	7	6	8	19	6	5	1	1	1	1
Częstość klasy Pj	0,12	0,10	0,14	0,34	0,10	0,09	0,018	0,018	0,018	0,018
Dystrybuanta Wj	0,12	0,23	0,38	0,72	0,83	0,92	0,94	0,96	0,98	1

Wartości oczekiwaną i wariancję oceniliśmy korzystając ze wzorów :

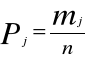
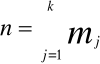
Częstość klasy obliczyliśmy ze wzoru:

Dystrybuantę obliczyliśmy ze wzoru:

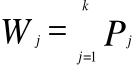
WYKRESY

Histogram częstości.

Wykres dystrybuanty.

Dobór rozkładu teoretycznego oraz weryfikacja hipotezy o zgodności.

Dokonaliśmy tego za pomocą programu LSP4, który realizuje następujące zadania :

• wczytanie wyników kontroli wymiarów detali,

• obliczenia wstępne i wydruk charakterystyk empirycznych,

• dobór rozkładu empirycznego i testowanie hipotezy o zgodności z rozkładami teoretycznymi,

• wydruk wyników końcowych.

WNIOSKI

W masowej produkcji jest niemożliwe sprawdzenie każdego detalu w zakresie dokładności jego wykonania, dlatego też sprawdza się dokładnie tylko pewną próbkę n - elementową wybraną w sposób losowy z całej produkcji. Ten sposób postępowania nazywa się statystyczną kontrolą jakości i stąd też wynika potrzeba nabycia umiejętności wyznaczania charakterystyk zmiennych losowych. W celu wyeliminowania błędów grubych posłużyliśmy się testem Romanowskiego, który w zależności od przyjętego poziomu istotności alfa decyduje o ilości danych eksperymentalnych dopuszczonych do dalszej analizy.

W naszym przypadku badany rozkład empiryczny okazał się niezgodny z teoretycznym rozkładem normalnym. Przy teście Romanowskiego dla poziomu istotności α=0,02 rozkład normalny nie został przyjęty.. Wyniki przeprowadzonych przez nas testów zawarte są w dołączonym przez nas wydruku komputerowym.Jak widać istotnym elementem testów jest dobór odpowiedniego poziomu istotności w teście Romanowskiego. Wiąże się on z liczbą danych przeznaczonych do dalszego testowania.

9

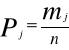
Stanowisko

przygotowane

zgodnie z rys.

Uzyskanie danych

z kontroli

wymiarów

Program

na IBM PC

---