LABORATORIUM Z PRZEDMIOTU

FIZYKA ATOMOWA

Temat:

Charakterystyka lampy neonowej;
Badanie drgań relaksacyjnych

Wydz. Matematyczno - Fizyczny

Kier. Fizyka Techniczna

Spec. Fizyka Ciała Stałego

Semestr VII

Rok Akademicki 2007/08

Toroń Bartłomiej

Katowice 17.11.2007

1. Cel ćwiczenia.

Celem ćwiczenia jest zapoznanie się z wyładowaniami w gazie rozrzedzonym i charakterystyką lampy neonowej, oraz pomiar drgań relaksacyjnych układu.

2. Wstęp teoretyczny

Do wytwarzania drgań relaksacyjnych wykorzystuje się procesy ładowania i rozładowania kondensatorów przez opór omowy R. W obwodzie po zamknięciu wyłącznika W napięcie U na kondensatorze o pojemności C będzie zmieniało się z czasem według równania:

Równolegle do kondensatora włączamy lampę neonową zwaną inaczej stabiliwoltem. Gaz wypełniający lampę nie przewodzi prądu elektrycznego poniżej pewnego napięcia zwanego napięciem zapłonu U_z. Napięcie to powoduje jonizację lawinową i przez lampę płynie prąd o natężeniu, którego wartość określa tylko opór zewnętrzny R. Obniżając napięcie przyłożone do świecącej neonówki doprowadzamy do jej zgaśnięcia i przy napięciu U_g zwanym napięciem gaśnięcia lampa zachowuje się jak doskonały izolator. W obwodzie takim napięcie na kondensatorze zmienia się w sposób piłokształtny, co jest wynikiem periodycznego ładowania i rozładowania kondensatora przez neonówkę.

3. Schemat układu pomiarowego.

Poniżej przedstawiono 3 schematy pomiarowe używane podczas pomiarów. Przy pomocy pierwszego z nich wyznaczono napięcie zapłonu i gaśnięcia lampy, przy pomocy drugiego wyznaczono charakterystykę prądowo napięciową neonówki, ostatni posłużył natomiast do badania drgań relaksacyjnych.

1)

2)

3)

4. Przebieg ćwiczenia.

Najpierw wyznaczono napięcia zapłonu i gaśnięcia neonówki. Pomiar powtórzono kilku krotnie, następnie wyznaczono dla 2 wartości rezystancji charakterystykę prądowo napięciową neonówki. Na końcu zmierzono ilość 20 „zaświeceń” neonówki by na tej podstawie określić własności drgań relaksacyjnych.

5. Otrzymane wyniki.

W poniższych tabeli przedstawiono wyniki pomiarowe uzyskane na laboratorium podczas pomiarów w przedstawionych powyżej układach pomiarowych:

- wyznaczenie napięcia zapłonu i gaśnięcia:

R= 300 kΩ		R= 600 kΩ
UZ [V]	Ug [V]	UZ [V]	Ug [V]
96	76,6	95,4	76,8
96,5	76,7	95,2	76,8
		95,9	76,8

-charakterystyka prądowo napięciowa:

R= 300 kΩ		R= 600 kΩ
U [V]	I [μA]	U [V]	I [μA]
95	0	95	0
100	0	100	0
105	36,9	105	79,6
110	44,0	110	95,1
115	52,8	115	109,9
120	61,2	120	125,6
125	68,4	125	136,8
130	78,9	130	152,6
135	86,0	135	170,2
140	93,8	140	186
145	101,3	145	202
150	109,3	150	228
145	101,4	145	205
140	91,9	140	181,8
135	84,7	135	164,9
130	76,4	130	149,4
125	69,6	125	130,1
120	59,8	120	115,8
115	51,8	115	99,8
110	44,1	110	85,3
105	36,7	105	68,6
100	27,5	100	54,1
95	0	95	42,4
90	0	90	23,7
85	0	85	0

-drgania relaksacyjne:

U0=97V	R= 300 kΩ			R= 600 kΩ
C [μF]	t1-300 [s]	t2-300 [s]	t3-300 [s]	t1-600 [s]	t2-600 [s]	t3-600 [s]
0,25	7,40	7,08	6,90	12,36	13,37	12,15
0,5	12,47	13,03	12,08	21,48	20,04	20,80
0,75	17,49	17,39	18,07	31,56	31,01	30,25
0,9	19,92	18,90	19,80	37,16	37,06	34,78
1	22,81	21,03	22,09	40,00	41,13	40,20
1,2	23,54	22,55	23,13	43,76	43,20	42,92
1,4	28,78	26,61	27,39	49,48	49,56	49,96
1,6	32,48	32,31	31,93	61,44	60,36	60,72
1,8	36,78	37,03	35,09	65,24	67,64	62,36
2	40,60	40,15	40,05	78,70	80,32	78,90

6. Opracowanie wyników.

1. Napięcia gaśnięcia / zapłonu neonówki i jej charakterystyka prądowo napięciowa

Ponieważ napięcie zapłonu i gaśnięcia było mierzone miernikiem bezpośrednio na neonówce nie zależy ono od wartości oporu R. W związku z tym wartość średnią i odchylenie standardowe jednocześnie dla R= 300 kΩ i R= 600 kΩ wyznaczamy ze wzoru:

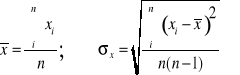
Wartości te są następujące:

	UZ [V]	Ug [V]
	96	76,6
	96,5	76,7
	95,4	76,8
	95,2	76,8
	95,9	76,8
	95,8000	76,74000
	0,230217	0,04000

Ostatecznie więc zgodnie z zasadami zaokrąglania:

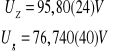
W celu wyznaczenia charakterystyki prądowo-napięciowej neonówki najpierw policzono niepewności otrzymanych wyników. Napięcie zasilania było mierzone miernikiem analogowym, zamontowanym fabrycznie w zasilaczu. W związku z tym niepewność pomiaru możemy obliczyć ze wzoru:

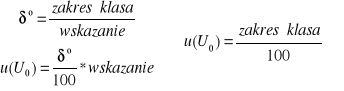
Zakres pomiarowy miernika wynosił 150V. Klasa przyrządu jest nieznana, jednakże z uwagi na jego zużycie, przyjmuję największą dopuszczalną klasę=5. W związku z tym w naszym przypadku:

Natężenie prądu natomiast było mierzone miernikiem cyfrowym więc możemy przyjąć (zakładając, że nie popełnia on błędów systematycznych, szczególnie multiplikatywnych), że błąd popełniany przy pomiarze jest błędem dyskretyzacji i wynosi on +/-1 najmniej znaczącej cyfry. Sporządzone charakterystyki prądowo napięciowe przedstawiono na poniższym rysunku:

2. Drgania relaksacyjne

Na początku obliczono wartość średnią i odchylenie standardowe 20 drgań zgodnie ze wzorami podanymi w pierwszej części opracowania wyników. Następie obliczono okres drgań, oraz wyznaczono jego niepewność. Podczas obliczeń przyjęto, że nie popełniono błędu przy liczeniu ilości zliczeń N=20. Faktycznie jedynie przy liczeniu drgań przy R= 300 kΩ i C=0,25 μF z uwagi na dużą częstotliwość drgań istniała możliwość popełnienia błędu. W pozostałych przypadkach drgania były na tyle wolne, że nie przyjęto, iż przy ich liczeniu nie popełniono błędów
. W związku z tym okres i jego niepewność obliczono ze wzoru:

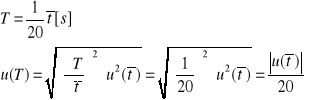
Wspomniane powyżej obliczenia przedstawiają poniższe tabele:

R= 300 kΩ
C [μF]	t1-300 [s]	t2-300 [s]	t3-300 [s]			T [s]	u(T) [s]
0,25	7,40	7,08	6,90	7,13	0,15	0,36	0,007311
0,5	12,47	13,03	12,08	12,53	0,28	0,63	0,013785
0,75	17,49	17,39	18,07	17,65	0,21	0,88	0,010599
0,9	19,92	18,90	19,80	19,54	0,32	0,98	0,016093
1	22,81	21,03	22,09	21,98	0,52	1,10	0,025848
1,2	23,54	22,55	23,13	23,07	0,29	1,15	0,014359
1,4	28,78	26,61	27,39	27,59	0,63	1,38	0,031731
1,6	32,48	32,31	31,93	32,24	0,16	1,61	0,008129
1,8	36,78	37,03	35,09	36,30	0,61	1,82	0,030464
2	40,60	40,15	40,05	40,27	0,17	2,01	0,008457
R= 600 kΩ
C [μF]	t1-600 [s]	t2-600 [s]	t3-600 [s]			T [s]	u(T) [s]
0,25	12,36	13,37	12,15	12,63	0,38	0,63	0,018829
0,5	21,48	20,04	20,80	20,77	0,42	1,04	0,020795
0,75	31,56	31,01	30,25	30,94	0,38	1,55	0,018989
0,9	37,16	37,06	34,78	36,33	0,78	1,82	0,03886
1	40,00	41,13	40,20	40,44	0,35	2,02	0,017408
1,2	43,76	43,20	42,92	43,29	0,25	2,16	0,012347
1,4	49,48	49,56	49,96	49,67	0,15	2,48	0,007424
1,6	61,44	60,36	60,72	60,84	0,32	3,04	0,015875
1,8	65,24	67,64	62,36	65,08	1,53	3,25	0,076315
2	78,70	80,32	78,90	79,31	0,51	3,97	0,025497

Na podstawie obliczonych wartości sporządzono wykresy T=f(C) dla obu wartości oporu oraz aproksymowano je prostą wyznaczoną za pomocą regresji liniowej ważonej, przy pomocy programu Origin 7.5.

Sporządzony wykres przedstawiono poniżej:

Program podał następujące parametry dopasowania:

Linear Regression for R=300kΩ:

Y = A + B * X

Weight given by R=300kΩ error bars.

Parameter Value Error

---------------------------------------------------------------

A 0,13843 0,00704

B 0,92685 0,00555

----------------------------------------------------------------

R SD N P

----------------------------------------------------------------

0,99846 3,28188 10 <0.0001

----------------------------------------------------------------

Linear Regression for R=600kΩ:

Y = A + B * X

Weight given by R=600kΩ error bars.

Parameter Value Error

----------------------------------------------------------------

A 0,1679 0,01534

B 1,71406 0,01209

-----------------------------------------------------------------

R SD N P

-----------------------------------------------------------------

0,98661 8,28311 10 <0.0001

-----------------------------------------------------------------

Wzory dopasowanych prostych:

1. R=300kΩ

gdzie:

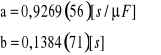
2. R=600kΩ

gdzie:

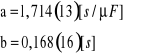
Na podstawie znajomości współczynników kierunkowych prostych można wyznaczyć stałą proporcjonalności:

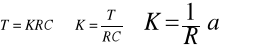
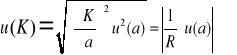
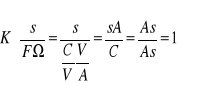
Po obliczeniu:

1. R=300kΩ

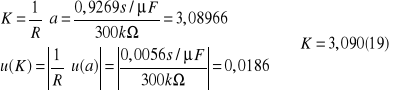
2. R=600kΩ

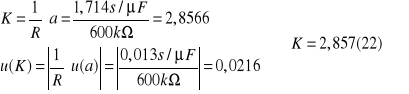
Powyższe wartości powinny być równe. W związku z tym uśredniając przy pomocy średniej ważonej, gdzie za wagi przyjęto kwadraty odwrotności niepewności poszczególnych składników otrzymujemy:

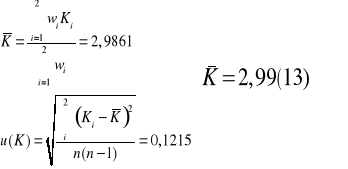
Z drugiej strony wartość stałej proporcjonalności K wynosi:

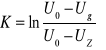
Jej niepewność:

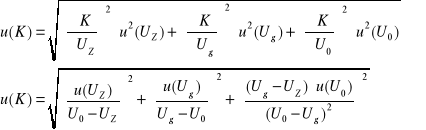
gdzie:

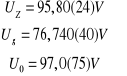
Po podstawieniu danych:

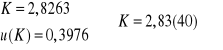
Przedziały wartości K uzyskane obiema metodami z uwzględnieniem niepewności posiadają pewną część wspólną. Można uśrednić te wyniki przy pomocy średniej ważonej, gdzie za wagi przyjmuje się kwadraty odwrotności niepewności poszczególnych składników, przy czym stałą k wyznaczoną z prostej regresji przyjmujemy 2 krotnie większą, gdyż zawiera ona w sobie dwie wartości stałej K policzonej dla 300 kΩ i 600 kΩ.

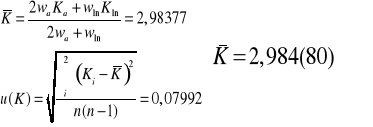
7. Wnioski.

Powyższe opracowanie wyników dokonano na podstawie wytycznych ze skryptu. Wydaje się jednak, iż poza wyznaczeniem charakterystyki prądowo-napięciowej neonówki, gdy prąd jest funkcją napięcia zasilania, przydałoby się wyznaczenie tej charakterystyki prądu jako funkcji napięcia na neonówce. Należałoby się spodziewać wtedy, iż charakterystyki będą prawie identyczne pomimo różnych wartości opornika R. Zmiana jego wartości zmieniałaby jedynie czułość układu, nie przesuwałaby natomiast charakterystyk względem siebie. Przesunięcie to wynika bowiem z II prawa Kirchoffa, gdyż zmienia się stosunek rezystancji połączonych szeregowo neonówki i kondensatora.

W wypadku drgań relaksacyjnych otrzymano stałą proporcjonalności między okresem drgań a wartością RC obwodu elektrycznego. Wyznaczono jej wartość K~3. Oznacza to, że w badanym obwodzie okres drgań jest 3 razy większy niż stała czasowa RC. Możliwe różnice od wartości oczekiwanej mogą wynikać z faktu, że należałoby zastanowić się czy nie dokonać regresji funkcji T=f(C)_z parametrem b=0. Teoretycznie taki warunek można nałożyć, jednak w rzeczywistym układzie nie da się wyeliminować zupełnie pojemności. Pewną pojemność ma zarówno neonówka jak i przyrządy pomiarowe i same kable, dlatego założenie b=0 nie koniecznie musiałoby poprawić wynik.

---