Wektory

Wektorem nazywamy uporządkowaną parę punktów. Pierwszy z tych punktów nazywamy początkiem wektora, a drugi końcem. Wektor o początku A i końcu B oznaczamy
,

wektory można też oznaczać
, itd. Jeżeli A = B to wektor nazywamy zerowym.

Wektory przedstawia się zazwyczaj na dwa sposoby:

ujęcie graficzne:  uzyskujemy przez narysowanie strzałki na płaszczyźnie lub w przestrzeni. ujęcie analityczne:  układ dwóch liczb - współrzędnych (na płaszczyźnie), lub trzech liczb (w przestrzeni)	związek między dwoma ujęciami wektora - strzałką wektora (ujęcie graficzne) i liczbami opisującymi położenie początku i końca strzałki.
Współrzędne wektora otrzymujemy odejmując od współrzędnych końca wektora, współrzędne początku tego wektora.	współrzędna x - owa wektora na rysunku ma wartość 7 (znajdujemy różnicę współrzędnych końca i początku wektora: 8 - 1 = 7). współrzędna y - owa w naszym wypadku ma wartość 4 (bo 6 - 2 = 4). Ostatecznie więc na powyższym rysunku mamy wektor [7,4].

Oba ujęcia - graficzne i analityczne - są równoważne, tzn. dają zgodne ze sobą wyniki. Zaletą ujęcia graficznego jest lepsze działanie na wyobraźnię, zaletą ujęcia analitycznego jest łatwość obliczeń matematycznych oraz możliwość tworzenia wektorów o więcej niż trzech wymiarach (znacznie trudniej byłoby wyobrazić sobie np. sześciowymiarowe wektory jako strzałki).

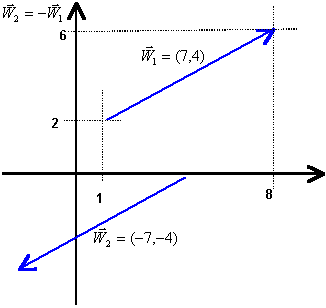
Wektory przeciwne

Dwa wektory są przeciwne wtedy, gdy jeden z nich powstaje przez "odwrócenie" drugiego - tzn. koniec pierwszego wektora staje się początkiem drugiego, a początek pierwszego wektora końcem drugiego.

Wektory przeciwne mają przeciwne współrzędne.

Np. wektorem przeciwnym do wektora [7,4] jest wektor [-7,-4].

Jak to widać z zapisu na rysunku wektor przeciwny do
jest zapisywany jako wektor   -
(minus W).

Cechy wektorów przeciwnych:

• są do siebie równoległe (mają takie same kierunki)

• mają takie same długości (wartości)

• mają przeciwne zwroty.

Suma dwóch wektorów przeciwnych równa jest zero (jest wektorem zerowym).

+ ( -
) = 0

Wektor jednostkowy

Bardzo ważnym rodzajem wektora jest wektor jednostkowy. Jest to wektor którego długość wynosi 1, a ustawienie w przestrzeni (ew. na płaszczyźnie) jest dowolne. Jest on najczęściej oznaczany literą - jako
, lub  e, czasem i, niekiedy jako jedynka ze strzałką na górze
  .

Wektor jednostkowy jest to idealnym narzędziem matematycznym do wskazywania kierunku, ponieważ zawiera w sobie całą informację o kierunku, przy pominięciu informacji o wartości.

Dowolny wektor
jest równy wektorowi jednostkowemu skierowanemu zgodnie z
pomnożonemu przez długość (wartość) w.

Wektor jednostkowy ma szczególne znacznie, dla osi współrzędnych. Wyznacza on jednostki tych osi.

 W przestrzeniach o ilości wymiarów większych niż 3 definicja wektora jednostkowego jest identyczna - tzn. wektor jednostkowy, będzie miał tyle składowych ile jest wymiarów, a długość będzie zawsze równa 1.

 Działania na wektorach

rodzaj działania	zapis i typ wielkości wynikowej	opis wielkości wynikowej
Dodawanie wektorów	Żeby dodać dwa wektory, gdy znamy ich współrzędne, należy dodać odpowiednie współrzędne - x-owe  do x-owych, a y-owe do y-owych (ew. z-owe do z-owych). Na płaszczyźnie (wx, wy) + (ux, uy) =  (wx+ux, wy+uy) W przestrzeni (wx, wy, wz ) + (ux, uy, uz) =  (wx+ux, wy+uy, wz + uz)	W odróżnieniu od dodawania liczb całkowitych wektor-suma wcale nie musi być dłuższy od któregoś z wektorów wyjściowych, a często bywa krótszy. Suma dwóch wektorów może być też wektorem zerowym (mimo, że wektory wyjściowe miały długości różne od zera). Zachodzi to  w dwóch przypadkach: - oba sumowane wektory są zerowe - dodawane wektory są przeciwne - tzn. mają ten sam kierunek i wartość, ale przeciwne zwroty.
Odejmowanie wektorów	Żeby odjąć dwa wektory, gdy znamy ich współrzędne, należy odjąć odpowiednie współrzędne - x-owe  od x-owych, a y-owe od y-owych (ew. z-owe od z-owych). Na płaszczyźnie (wx, wy) - (ux, uy) =  (wx - ux, wy - uy) W przestrzeni (wx, wy, wz ) - (ux, uy, uz) =  (wx - ux, wy - uy, wz - uz)	Wektor-różnica wcale nie musi być krótszy od pierwszego z wektorów wyjściowych. Może być dłuższy. Różnica dwóch wektorów jest równa zero (jest wektorem zerowym) w dwóch przypadkach: - oba odejmowane wektory są zerowe - odejmowane wektory są równe tzn. mają ten sam kierunek, zwrot i wartość.
mnożenie wektora przez liczbę Tak samo dzielenie przez liczbę.	otrzymujemy nowy wektor Aby wektor podzielić przez liczbę, mnożymy go przez odwrotność tej liczby	powstaje wektor a razy dłuższy od wektora wyjściowego. Zwrot wektora wynikowego jest: - taki sam jak wyjściowy, gdy a jest dodatnie - przeciwny do wyjściowego, gdy a jest ujemne Wynik może być równy zero (będzie tzw. wektorem zerowym) gdy: - wektor wyjściowy jest równy zero, lub - liczba a jest równa zero
mnożenie skalarne wektorów	otrzymujemy skalar	Powstaje liczba (skalar) o wartości równej iloczynowi wartości obu wektorów razy kosinus kąta między nimi zawartego. Lub inaczej: Iloczyn skalarny jest równy iloczynowi długości jednego wektora mnożonego przez długość rzutu drugiego wektora na kierunek wyznaczony przez pierwszy wektor (skomplikowane jest to zdanie, ale prościej chyba się nie da...). Iloczyn skalarny stanie się równy Zero, gdy którykolwiek z wektorów wyjściowych jest zerowy, lub wektory są do siebie prostopadłe.
mnożenie wektorowe wektorów (stosuje się  wyłącznie do wektorów w trzech wymiarach)	otrzymujemy nowy wektor prostopadły do obu wektorów wyjściowych. Długość (wartość) tego wektora wynosi:	- wartość wektora wynikowego jest równa iloczynowi wartości obu wektorów wyjściowych razy sinus kąta między nimi zawartego (ma to sens tylko w trzech wymiarach); - kierunek wektora wynikowego jest prostopadły do płaszczyzny wyznaczonej przez wektory wyjściowe; - zwrot ustalamy w oparciu o regułę śruby prawoskrętnej Interpretacja iloczynu wektorowego 2: Wartość iloczynu wektorowego jest równa iloczynowi długości pierwszego wektora przez długość rzutu drugiego wektora na kierunek prostopadły do pierwszego wektora. Wektor zerowy otrzymamy, gdy jeden z wektorów wyjściowych jest zerowy, lub gdy wyjściowe wektory są równoległe.
znajdowanie wartości (długości) wektora gdy znamy jego współrzędne	Długość wektora na płaszczyźnie obliczamy stosując twierdzenie Pitagorasa.  Żeby obliczyć wartość wektora trójwymiarowego trzeba zastosować to twierdzenie dwa razy.	Długość wektora jest równa zero tylko wtedy, gdy wszystkie współrzędne wektora są równe zero.

Dodawanie algebraiczne wektorów

Dodawanie wektorów zapisanych w postaci liczbowej (algebraicznej) polega na zwykłym dodawaniu ich odpowiednich współrzędnych. Czyli:

(w_x, w_y) + (u_x, u_y) =  (w_x+u_x, w_y+u_y)

Przykłady

Np. gdy mamy wektory:

= [2 , 3]

= [5 , 1]

To ich sumę obliczamy następująco:

+ 
= [2 , 3] + [ 5 , 1] = [2 + 5 , 3 + 1] = [7 , 4]

 

Gdyby wektorów było więcej, to musielibyśmy dodać współrzędne wszystkich wektorów:

= [2 , 3]

= [5 , 1]

= [3 , -9]

Teraz sumę obliczamy tak:

+
+
= [2 , 3] + [ 5 , 1] + [3 , -9] = [2 + 5  + 3, 3 + 1 - 9]=[10 , -5]

W celu graficznego dodania wektorów (czyli wektorów narysowanych jako strzałki), powinniśmy zastosować jedną z dwóch metod (można wybrać tę, która wygodniejsza w danej sytuacji):

• reguła równoległoboku

• reguła trójkąta

Reguła równoległoboku dodawania wektorów

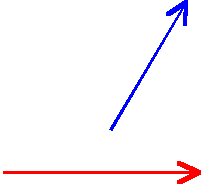
Załóżmy, że początkowo mamy dwa różne wektory

- niebieski i czerwony:

Wektory zaczepiamy we wspólnym początku (kierunek, zwrot i długość obu wektorów nie mogą ulec zmianie). Trzeba przenieść (zachowując jego kierunek i zwrot) jeden z wektorów do początku drugiego

Przez koniec pierwszego wektora prowadzimy prostą równoległą do drugiego wektora, a następnie przez koniec drugiego wektora prowadzimy równoległą do pierwszego wektora.

Wspólny początek wektorów (początek wektora-sumy) łączymy z punktem przecięcia prostych z utworzonych na etapie poprzednim (będzie to koniec wektora-sumy)

 

Reguła trójkąta dodawania wektorów

Załóżmy znowu, że, jak poprzednio, początkowo mamy dwa wektory:

Początek jednego wektora zaczepiamy w końcu drugiego wektora. Musimy po prostu przenieść jeden wektor zachowując jego kierunek, zwrot i długość.

Początek pierwszego wektora (będzie to początek wektora-sumy) łączymy z końcem drugiego wektora (będzie to koniec wektora-sumy).

Gotowe! - wektor zielony jest sumą wektorów - niebieskiego i czerwonego

 

Dodawanie graficzne wektorów - przykłady:

 

 

 

Dodawanie wektorów mających ten sam kierunek

W przypadku, gdy oba wektory leżą na jednej prostej nie da się wykreślić równoległoboku ani (rozsądnie wyglądającego) trójkąta. Wtedy posługujemy się metodą zbliżoną zasadami do metody trójkąta, jednak nieco inaczej się prezentującą:

Sytuacja początkowa - mamy dwa wektory o takim samym kierunku

Przenosimy jeden wektor zaczepiając jego początek w końcu drugiego wektora (tak jak w regule trójkąta).

 

Wektor suma (na rysunku zielony) - ma początek w początku pierwszego, a koniec w końcu drugiego wektora:

 

Przypadek wektorów o przeciwnych zwrotach

Trochę inaczej wygląda dodawanie wektorów różniących się zwrotami.

Wtedy po przeniesieniu początku jednego wektora do końca drugiego, uzyskamy częściowe pokrywanie się strzałek obu tych wektorów.

Co nie zmienia sytuacji, że wektor - suma będzie miał początek w początku pierwszego, a koniec w końcu drugiego wektora:

Graficzne odejmowanie wektorów

Graficzne odejmowanie wektorów jest podobne do operacji ich dodawania. Różnica zawiera się w tym, że: odejmowanie wektora polega na dodaniu wektora przeciwnego. 

Przykład:

Mamy początkowo dwa wektory - czerwony i niebieski:

Aby od wektora czerwonego odjąć wektor niebieski, należy:

1. odwrócić wektor niebieski, czyli znaleźć wektor do niego przeciwny.

Na powyższym rysunku wektor narysowany linią przerywaną jest wektorem wyjściowym, a wektor przeciwny został narysowany linią ciągłą.

2. Dodać ten odwrócony wektor do wektora czerwonego (dowolną prawidłową metodą).

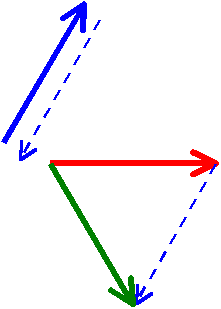
Na rysunku obok efektem odejmowania wektora niebieskiego od wektora czerwonego jest wektor zielony.
Wektor początkowy jest on tym zaznaczony na niebiesko (linia ciągła) i pogrubiony (znajduje się w pozycji wyjściowej).

 

Odejmowanie wektorów metodą trójkąta

W przypadku, gdy oba wektory, które mamy odjąć są początkowo zaczepione w tym samym punkcie, wtedy odejmowanie jest bardzo proste i szybkie.

Bo wtedy różnica tych wektorów powstanie po prostu po połączeniu końców ich strzałek. Początek wektora - różnicy jest w końcu wektora odejmowanego, a koniec w końcu wektora od którego następuje odejmowanie.

Na powyższym rysunku wektor zielony jest różnicą wektorów czerwonego i niebieskiego.

Przykłady działań na wektorach w postaci analitycznej

Dane odnoszące się do przykładów poniżej:
Wektory wyjściowe:




Liczba:
a = 3

Wektor wynikowy: 

liczba wynikowa: c

Rodzaj działania	zapis	Przykład i komentarz
Dodawanie wektorów		(2 + 3, 5 + (-7)) = (5, -2) Dodajemy odpowiednie współrzędne. Z = (5, -2)
Odejmowanie wektorów		(2 - 3, 5 - (-7)) = (-1, 5 + 7) = (-1, 12) Odejmujemy odpowiednie współrzędne. Z =  (-1, 12)
mnożenie wektora przez liczbę		3 ∙ (2,5) = (6,15) mnożymy przez liczbę, każdą ze współrzędnych wektora. Z = (6,15)
Mnożenie skalarne wektorów	c = wx ∙ vx + wy∙ vy	(2,5) ∙ (3,-7) = 6+(-35)=-29 mnożymy przez siebie współrzędne obu wektorów, a otrzymane iloczyny dodajemy
mnożenie wektorowe wektorów	Wartość wektora Z można obliczyć ze wzoru:	Wartość iloczynu wektorowego wektorów (2,5) i (3,-7) |(2,5) x (3,-7)| = |-14 -15|=|-29|=29 Aby otrzymać wartość iloczynu wektorowego, mnożymy współrzędne "na krzyż", otrzymane iloczyny odejmujemy i wyciągamy wartość bezwzględną z wyniku.
znajdowanie wartości wektora	na płaszczyźnie: w przestrzeni: otrzymujemy skalar	Podnosimy współrzędne do kwadratu, wyniki dodajemy, a otrzymaną sumę pierwiastkujemy.

Mnożenie skalarne wektorów

Mnożenie skalarne wektorów jest działaniem na dwóch wektorach będących pod pewnym kątem do siebie.

Mnożenie skalarne zapisujemy po prostu kropką mnożenia między symbolami wektorów.

Wynikiem mnożenia skalarnego jest liczba (skalar) o wartości równej iloczynowi wartości obu wektorów razy kosinus kąta między nimi zawartego.

 

Interpretacja mnożenia skalarnego

Iloczyn skalarny można zinterpretować także jako wartość iloczynu wartości wektorów przypadającą na ten sam kierunek. Inaczej mówiąc mnożąc przez siebie skalarnie wektory siły i długości dowiemy się pośrednio jak bardzo siła działa w kierunku wektora długości.

Jeszcze inaczej iloczyn skalarny można zinterpretować, jako wartość równą iloczynowi długości jednego wektora mnożonego przez długość rzutu drugiego wektora na kierunek wyznaczony przez pierwszy wektor (skomplikowane jest to zdanie, ale prościej chyba się nie da...).

Zapiszmy to może wzorem opisowym:

iloczyn skalarny =

długość_wektora_1 * długość_rzutu_wektora_2_na_kierunek_wektora_1

 

Mnożenie skalarne wektorów - przypadki szczególne

Iloczyn skalarny stanie się równy zero, gdy zachodzi przynajmniej jeden z przypadków:

• którykolwiek z wektorów wyjściowych jest zerowy, 

• wektory są do siebie prostopadłe.

 

Jeżeli wektory wyjściowe są równoległe, to iloczyn skalarny jest równy po prostu iloczynowi ich długości. 

Dowolny wektor pomnożony skalarnie przez samego siebie da w wyniku kwadrat swojej wartości:

---