CIĄGI LICZBOWE
DEF.1. Ciągiem liczbowy nazywamy funkcję f , która przyporządkowuje każdej liczbie naturalnej pewną wartość liczbową. Wartość funkcji f dla argumentu n∈ N f(n) nazywamy n -tym wyrazem ciągu i piszemy an.
DEF.2.Mówimy, że ciąg an jest:
Rosnący (silnie rosnący) jeżeli
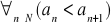
Niemalejący (słabo rosnący) jeżeli
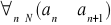
Malejący (silnie malejący) jeżeli
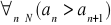
Nierosnący (słabo malejący) jeżeli
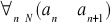
DEF.3. Ciąg monotoniczny to taki, który posiada jedną z własności z DEF.2.
DEF.4. Mówimy, że ciąg an jest ograniczony z góry jeżeli
![]()
DEF.5. Mówimy, że ciąg an jest ograniczony z dołu jeżeli
![]()
DEF.6. Mówimy, że ciąg an jest ograniczony jeżeli
![]()
DEF.7. Jeżeli (an) i (bn) są dwoma dowolnymi ciągami to :
(an + bn) jest sumą ciągów
(an - bn) jest różnicą ciągów
(an · bn) jest iloczynem ciągów
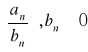
jest ilorazem ciągów
DEF.8.Ciąg liczbowy nazywamy arytmetycznym jeśli dla dowolnego a1 :
![]()
.
Stąd też ![]()
dla n>1 oraz
![]()
DEF.9.Ciąg liczbowy nazywamy geometrycznym jeśli dla dowolnego a1 :
![]()
.
Stąd też ![]()
dla n>1 oraz
![]()
DEF.10. Otoczenie otwarte liczby x0 nazywamy przedział otwarty (x0-r, x0+r) , r>0.
DEF.11. Otoczenie domknięte liczby x0 nazywamy przedział domknięty [x0-r, x0+r] , r>0.
DEF.12. Otoczenie plus nieskończoności nazywamy przedział (A,∞), A∈R.
DEF.13. Otoczenie minus nieskończoności nazywamy przedział (-∞,A), A∈R.
Przykład.1.Co oznacza, że liczba y należy do otoczenia otwartego liczby x0 ?
Oznacza to, że
x0-r < y < x0+r
r < y- x0 < r
| y- x0 |< r
DEF.14.Liczba g jest granicą ciągu an jeżeli do dowolnie małego otoczenia liczby g należą prawie wszystkie wyrazy tego ciągu co zapisujemy ![]()
lub ![]()
. Zapisujemy:
![]()
Prawie wszystkie wyrazy ciągu oznacza wszystkie wyrazy ciągu z wyjątkiem co najwyżej skończenie wielu.
Przykład.2.Czy prawdą jest, że prawie wszystkie wyrazy ciągu liczb naturalnych są
dodatnie -TAK
większe od miliona - TAK
niepodzielne przez milion -NIE.
Twierdzenie 1. Każdy ciąg ma co najwyżej jedną granicę.
Uwaga1. Ciąg, który ma granicę jest zbieżny. Ciąg, który nie ma granicy jest rozbieżny.
Twierdzenie 2. Każdy ciąg zbieżny jest ograniczony.
Uwaga 2. Twierdzenie odwrotne do 2 jest fałszywe. Ciąg (-1)n jest ograniczony ale nie jest zbieżny.
Twierdzenie3. Każdy ograniczony i monotoniczny ciąg jest zbieżny.
Twierdzenie4. Każdy podciąg wybrany z ciągu zbieżnego jest zbieżny do tej samej granicy do której jest zbieżny ciąg.
WARUNEK CAUCHY'EGO
![]()
Twierdzenie5. Ciąg an jest zbieżny (ma granicę) wtedy i tylko wtedy gdy spełnia warunek Cauchy'ego.
DEF.15.Mówimy, że ciąg an jest rozbieżny do +∞ albo ciąg an ma granicę (niewłaściwą) jeżeli każde otoczenie plus nieskończoności zawiera prawie wszystkie wyrazy ciągu an piszemy ![]()
.
DEF.16.Mówimy, że ciąg an jest rozbieżny do -∞ albo ciąg an ma granicę (niewłaściwą) jeżeli każde otoczenie minus nieskończoności zawiera prawie wszystkie wyrazy ciągu an piszemy ![]()
.
Twierdzenie 6.Jeśli
![]()
oraz ![]()
wówczas
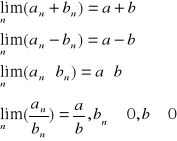
Twierdzenie 7. Granicą ciągu stałego (c) jest liczba c.
Twierdzenie 8.(o trzech ciągach) Jeśli dane są ciągi an , bn , cn ,których wyrazy dla wszystkich n≥n0 spełniają nierówność:
an ≤ bn , ≤ cn
i jeśli
![]()
to:
![]()
Uwaga 3.
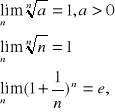
ZADANIA
Oblicz pięć początkowych wyrazów ciągu:
(a)an=![]()
(b)bn=n-3n2 (c)cn=![]()
(d)dn=![]()
(e)en=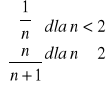
(f) fn=5
(g)g1=3, g2=5, a dla >2 gn=![]()
(h)bn=4n-2
(i) dn=![]()
(j)g1=1, g2=1, gn= gn-2+ gn-1 (k)hn=6⋅(-2)n-1
PRZYKŁAD:
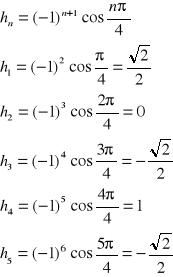
Zapisz wyraz ogólny ciągu
(a)(2,4,6,8,....) (b)(1/3,1/6,1/9,1/12,1/15,...) (c)(-1,2,-3,4,-5,...)
(d)(9,9,9,9,...) (e)(1,3,9,27,…) (f)(1,-1,-3,-5,-7,…)
(g)(-1,5,-25,125,…) (h)(4,4.5,5,5.5,….) (i)(4,2,1,1/2,1/4,….)
Zbadać czy są monotoniczne ciągi o wyrazie ogólnym
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e)![]()
(f)an=![]()
(g)an=![]()
PRZYKŁAD:
![]()
Aby zbadać monotoniczność ciągu an należy określić znak wyrażenia an- an+1, więc
![]()
więc ciąg an jest malejący.
Zbadać czy ciągi są ograniczone:
(a) ![]()
(b) ![]()
(c) ![]()
(d) ![]()
(e)![]()
(f)an=![]()
(g)an=![]()
PRZYKŁAD:
![]()
Gdyby ciąg an był ograniczony to istniały by stały m i M takie, że wszystkie wyrazy tego ciągu mieściły by się między tymi stałymi. Wypiszmy początkowe wyrazy ciągu. Są to: 1,3/5,3/7,3/9,.....,3.201,..... Zauważmy, że ciąg jest malejący więc wyraz pierwszy jest największe i wszystkie wyrazy są dodatnie. Więc istnieją stałe ograniczające ciąg czyli
![]()
Zbadaj na podstawie definicji ciągu czy:
(a)![]()
(b)![]()
(c)![]()
(d)![]()
(e)![]()
(f)![]()
PRZYKŁAD:
![]()
Musimy znaleźć k dla ε
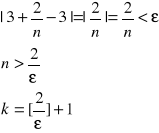
Niech ε=0.01 wtedy k=201 czyli wyrazy , których indeksy są większe od 201 należą do otoczenia liczby 3.
Niech ε=0.005 wtedy k=401 czyli wyrazy , których indeksy są większe od 401 należą do otoczenia liczby 3.
Gdyby
![]()
Musimy znaleźć k dla ε
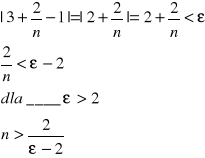
i mamy sprzeczność gdyż ε>2 a z założenia musi być dowolne.
Oblicz granicę ciągu o wyrazie ogólnym
(1)![]()
(2)![]()
(3)![]()
(4)![]()
(5)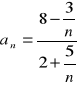
(6)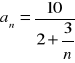
(7)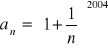
(8)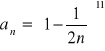
(9)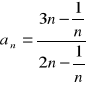
(10)![]()
(11)![]()
(12)![]()
(13)![]()
(14)![]()
(15)![]()
(16)![]()
(17)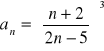
(18)![]()
(19)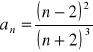
(20)![]()
(21)![]()
(22)![]()
(23)![]()
(24)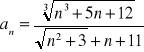
(25)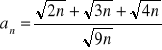
(26)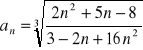
(27)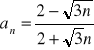
(28)![]()
(29)![]()
(30)![]()
(31)![]()
(32)![]()
(33)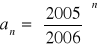
(34)![]()
(35)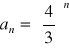
(36)![]()
(37)![]()
(38)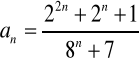
(39)![]()
(40)![]()
(41)![]()
(42)![]()
(43)![]()
(43)![]()
(44)![]()
(45)![]()
(46)![]()
(47)![]()
(48)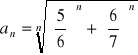
(49)![]()
(50)![]()
(51)![]()
(52)![]()
(53)![]()
(54)![]()
(55)![]()
(56)![]()
(57)![]()
(58)![]()
(59)![]()
(60)![]()
(61)![]()
(62)![]()
(63)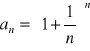
(64)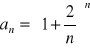
(65)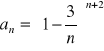
(66)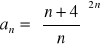
(67)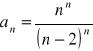
Wyszukiwarka
Podobne podstrony:
WIELOMIANY, Zadania przygotowujące do matury z matematyki
WIELOMIANY, Zadania przygotowujące do matury z matematyki
Ciągi- wzory warunki, Do Matury, Matematyka
Zadania przygotowawcze do egzaminu z matematyki
Bukiety matematyczne dla gimnazjum zadania przygotowujące do konkursów
ZADANIA PRZYGOTOWAWCZE DO EGZAMINU, SGGW TRiL, Matematyka tril sggw
Bukiety matematyczne dla gimnazjum zadania przygotowujące do konkursów
wielomiany, Do Matury, Matematyka
matma- geometria analityczna- powtórka, Do Matury, Matematyka
Zadania przygotowujące do egzaminu
matma wzory, Do Matury, Matematyka
(ebook www zlotemysli pl) psychologiczne przygotowanie do matury fragment AVRDNVSIWP7PVXYZFCBGDCEJQC
kalendarz przygotowan do matury polski pp
Zadania Przygotowawcze do Kolokwium-09--p2
PRZYGOTOWANIE DO MATURY
Kalendarz przygotowań do matury z WOS III c 2009(1)
więcej podobnych podstron