PROGNOZOWANIE I SYMULACJA(E) W PRZEDSIĘBIORSTWIE
Istnieje wiele różnych metod rozwiązywania modeli matematycznych tzn. wyznaczania rozwiązań optymalnych lub prawie optymalnych.
Rozróżnia się trzy zasadnicze metody:
Metody algorytmiczne,
Metody symulacyjne,
Metody heurystyczne
Metody algorytmiczne
Algorytm to zbiór procedur lub reguł matematycznych, które stosowane krok po kroku doprowadzają do uzyskania najlepszego rozwiązania modelu.
Metody algorytmiczne są najpowszechniejszą procedurą rozwiązywania zadań.
Metody heurystyczne
W przypadkach, kiedy matematyczne sformułowanie problemu jest tak złożone, że stosowanie metod analitycznych jest prawie niemożliwe, a metody symulacyjne ze względu na długi okres trwania symulacji są niepraktyczne, stosuje się metody heurystyczne.
Przez heurystyczny proces rozwiązywania rozumie się wykorzystanie w modelu pewnych intuicyjnych i empirycznie uzasadnionych reguł w celu otrzymania rozwiązania
Metody symulacyjne
Wielu problemów nie można rozwiązać metodami analitycznymi, tzn. matematycznymi.
W takich przypadkach stosowane są metody symulacyjne, jednak rozwiązania uzyskane w procesie symulacji nie zawsze są rozwiązaniami optymalnymi.
Kilka słów Wstępu
Podejmując decyzję gospodarczą - ekonomista (każdy z nas) bierze pod uwagę okoliczności, jakie będą towarzyszyły w przyszłości przekształcaniu tej decyzji w realizację:
świadom tego lub nie - przewiduje przyszłość
Symulacja oznacza wykorzystanie zestawu zróżnicowanych technik badawczych, zasadzających się na wprawieniu w ruch modelu naśladującego zachowanie badanego systemu.
Dzięki symulacji uzyskuje się możliwość obserwacji zjawisk gospodarczych i eksperymentowania
z nimi w sposób, który wydawał się dotychczas możliwy tylko w naukach eksperymentalnych
Budowa i uruchomienie modelu symulacyjnego pozwala na obserwację dynamiki modelowanego systemu
w warunkach kontrolowanych przez eksperymentatora.
Dodajmy, że eksperymentator może zmieniać warunki tak, aby przetestować zasadność badanych hipotez.
Symulacja stwarza laboratorium, w którym możemy analizować problemy ekonomiczne w sposób, w jaki w rzeczywistości nigdy tego nie moglibyśmy zrobić.
Jedną z ważnych dziedzin zastosowania symulacji jest prognozowanie.
Symulacja pozwala na przeprowadzenie pogłębionej analizy właściwości modelu przedstawiającego badany system, czym prowadzi do uściślenia przewidywań dotyczących zachowania się modelu.
Obserwacja modelu, a w szczególności pomiar jego właściwości pozwala na przewidywanie reakcji czy właściwości modelowanego systemu.
To, jak dalece model jest podobny do modelowanego systemu, rzutuje na dokładność wniosków o właściwościach modelowanego systemu.
Model
Systemy występujące wokoło nas - a także zachodzące
w nich procesy - są niekiedy tak złożone, że ich zrozumienie sprawia nam poważne trudności
(a czasem wręcz przekracza nasze możliwości).
Opisując badany system z pominięciem mniej istotnych jego elementów tworzymy model - nowy system, uproszczony, a przez to łatwiejszy do zrozumienia.
Zrozumiawszy model, łatwiej zrozumiemy modelowany system. Posługiwanie się modelem często okazuje się tańsze, niekiedy szybsze lub bezpieczniejsze.
W przypadku systemów nieistniejących
(czy to jeszcze nie powstałych, jak np. prom kosmiczny w fazie projektowania, czy też już należących do przeszłości, jak np. atmosfera Ziemi z okresu, gdy rodziło się życie) symulacja modelu może stwarzać jedyną szansę badań.
Istotną cechą modelu jest to, że stanowi on uproszczony opis rzeczywistości. Zakres uproszczeń oraz ich skala wyznaczone są celami, dla których model jest budowany.
Model analogowe i cyfrowe
W zależności od tworzywa, z jakiego są ukształtowane możemy podzielić modele na analogowe oraz cyfrowe
Modele analogowe (nazywane też modelami fizycznymi) mogą być zbudowane z tego samego tworzywa, co modelowany system (np. w modelu Portu Północnego, zbudowanym przed podjęciem prac nad budową samego portu, tworzywem były beton (falochrony i nabrzeża), woda wypełniająca model oraz piasek (dno portu), lub z tworzywa innego (np. model karoserii samochodu przeznaczony do badań aerodynamicznych budowany jest z plastiku, drewna czy papieru).
W modelach cyfrowych, zwanych też numerycznymi, tworzywem są liczby, zmienne
i wiążące je relacje.
Modele cyfrowe są zbudowane z matematycznych relacji: równań, nierówności, warunków logicznych, tabel, wykresów, opisujących zachowanie się zmiennych endogenicznych modelowanego systemu i ich reakcje na zmiany otoczenia reprezentowanego przez zmienne egzogeniczne.
Zmienne występujące w modelach mogą przyjmować
wartości ciągle lub dyskretne (skokowe).
Względy praktyczne zmuszają czasem do przybliżenia zmiennej ciągłej zmienną dyskretną. Nazywamy to dyskretyzacją zmiennej (np. zmienna ciągła, jaką jest wzrost każdego z nas, zapisywana jest w dokumentach w postaci zdyskretyzowanej -
w zaokrągleniu do pełnych centymetrów).
Zmienne modelu mogą być
ciągłe lub dyskretne w czasie.
W pierwszym przypadku wartości zmiennej są określone w każdym momencie czasu, w drugim przypadku są określone w wybranych momentach czasu. Momenty te jak gdyby tną czas w plasterki.
Odległości pomiędzy kolejnymi momentami mogą być stałe lub zmienne. Analiza wartości przyjmowanych przez zmienne modelu może odbywać się w równooddalonych momentach.
Odstęp czasu dt zbyt długi sprawia, że przybliżenie trajektorii zmiennych modelu okazuje się nazbyt ziarniste, czasem pozbawione ważnych szczegółów opisujących zmiany zachodzące w systemie w okresie krótszym od dt.
Odstęp dt zbyt krótki zmusza do zatrzymywania symulacji modelu i badania wartości jego zmiennych w odcinkach na tyle krótkich, że żadne ważne zmiany stanu badanego systemu nie miały możliwości się zrealizować. Wydłuża to czas eksperymentu oraz zwiększa objętość wygenerowanych wyników.
Model analogowy najczęściej działa
w sposób ciągły w czasie, natomiast rejestracja wyników dokonywana jest
w sposób dyskretny, w wybranych momentach czasu.
Mówimy wówczas o dyskretyzacji zmiennej w czasie. Dyskretyzacja w czasie jest typowa dla modeli cyfrowych.
Dla modeli matematycznych (zwłaszcza liniowych)
ze zmiennymi ciągłymi można znaleźć formuły analityczne opisujące trajektorie, po jakich biegną zmienne endogeniczne,
tj. rozwiązanie analityczne
ciągłe w czasie.
Modele matematyczne mogą jednak być na tyle skomplikowane, że znalezienie rozwiązania analitycznego jest bądź bardzo trudne, bądź wręcz niemożliwe.
Ograniczamy się wówczas do numerycznego poszukiwania rozwiązań, wyliczając współrzędne punktów leżących na trajektoriach zmiennych objaśnianych.
Także i w tym przypadku mamy do czynienia z dyskretyzacją w czasie zmiennej ciągłej.
Ważnym elementem modelu są jego parametry, charakteryzujące siłę, z jaką jedna zmienna reaguje na zmianę innej zmiennej. Parametry te są w zasadzie wielkościami stałymi.
Realizm modelu wymaga, aby parametry miały wartości możliwie bliskie wartościom
w populacji generalnej, zatem przed wykorzystaniem modelu do symulacji jego parametry muszą zostać oszacowane lub uzyskane w inny sposób, np. przez kalibracje, analizę porównawczą, rozumowanie per analogiam, itd..
Wiele modeli stosowanych w symulacji zawiera elementy losowe, sprawiające, iż przewidywania oparte na takich modelach nie są wyznaczone z całkowitą pewnością.
W symulacji deterministycznej elementy losowe traktowane są jako znane (zastępowane np. wartościami oczekiwanymi).
W symulacji stochastycznej losowe elementy modelu podlegają samodzielnemu modelowaniu, a proces ich generowania staje się istotnym elementem składowym symulacji.
Symulacja, zwłaszcza stochastyczna, generuje znaczną ilość wyników.
Ważnymi elementami procesu symulacji, wpływającym na użyteczność otrzymanych wyników są:
Opracowanie wyników symulacji;
Wybór miar pozwalających na ocenę jakości zachowania się modelu
Prognozowanie a symulacja
Prognozowanie i symulacja wzajemnie się uzupełniają
i wspomagają. W wielu przypadkach prognozy wyliczamy
przez symulację, czyli wprawienie w ruch modelu.
Nie zawsze jednak prognozowanie musi posiłkować się symulacją. Z wielu modeli można wyznaczyć prognozy bez pośrednictwa symulacji, można też prognozować bez wykorzystywania modelu.
(Symulację zaś można zastosować do celów innych niż prognozowanie, np. w statystyce - do oceny zachowania się zmiennych losowych mających rozkłady nie dające się wyrazić matematycznie, w matematyce - do poszukiwania pola obszaru ograniczonego krzywą o nieregularnym kształcie).
Modele zdarzeń dyskretnych a modele procesów ciągłych
Modele zdarzeń dyskretnych opisują zjawiska raczej mikroekonomiczne, będące szczególnie często przedmiotem zainteresowania badań operacyjnych.
Modele procesów ciągłych, często stosowane do opisu zjawisk makroekonomicznych, w większości przypadków mają charakter układów równań różniczkowych, bądź różnicowych.
SYMULACJA
Słowo symulacja jest dziś używane w bardzo wielu znaczeniach.
Przegląd definicji ilustruje zróżnicowanie znaczeń, w jakich używane jest to słowo. Dla ustalenia uwagi przyjmiemy, że symulacja to wprawienie modelu w ruch.
Do najważniejszych okoliczności towarzyszących podejmowaniu optymalnych decyzji gospodarczych należy ocena skutków tych decyzji.
Do oceny skutków można podejść na dwa sposoby:
1. przez eksperyment fizyczny na rzeczywistym systemie
2. przez eksperyment intelektualny (numeryczny) na modelu systemu.
Sposób pierwszy (eksperyment fizyczny) polega na wdrożeniu wybranego wariantu rozważanej decyzji, a więc wykonaniu eksperymentu na badanym systemie gospodarczym (przedsiębiorstwie, grupie przedsiębiorstw, gospodarce narodowej, etc.).
W praktyce gospodarczej zdarzają się eksperymenty, np. zastosowanie na szczeblu przedsiębiorstwa różnych technik reklamy oraz marketingu celem późniejszego porównania rezultatów różnych rozwiązań.
Jest to jednak sposób
kosztowny,
pracochłonny,
czasochłonny,
a co ważniejsze - potencjalnie dolegliwy, a nawet niebezpieczny, gdyż ewentualne niekorzystne skutki eksperymentu dotykają uczestniczących w nim żywych ludzi.
Szczególnym utrudnieniem wydaje się tu być konieczność uwzględnienia wpływu wszystkich parametrów czy zmiennych, istotnie wpływających na zróżnicowanie wyników eksperymentu.
Nawet przy niewielkiej liczbie zmiennych i parametrów, warunkujących reakcje, wypadałoby zrealizować znaczną liczbę wariantów eksperymentu, co bardzo podwyższa koszty badania.
Sposób drugi (eksperyment intelektualny)
polega na eksperymencie przy wykorzystaniu modelu wiążącego interesujące nas zmienne objaśniane, reagujące na rozważaną decyzję, ze zmiennymi objaśniającymi, będącymi iParametry modelu mogą zostać oszacowane na podstawie informacji zgromadzonej w wyniku obserwacji zachowania się badanego systemu. Parametry te mogą też być przyjęte na podstawie opinii ekspertów, oparte na założeniach itd.
instrumentem realizacji tej decyzji.
Parametry modelu mogą zostać oszacowane na podstawie informacji zgromadzonej w wyniku obserwacji zachowania się badanego systemu. Parametry te mogą też być przyjęte na podstawie opinii ekspertów, oparte na założeniach itd.
Badanie symulacyjne ma tą przewagę, że może być prowadzone na modelu systemu już nie istniejącego (np. analogowy model atmosfery ziemskiej sprzed trzech miliardów lat wykorzystano do badania możliwości samorzutnego powstania aminokwasów - jednych z najprostszych związków organicznych),
bądź też systemu jeszcze nie istniejącego
(np. model cyfrowy kadłuba promu kosmicznego wykorzystano do badań zdolności skutecznego wyhamowania promu, w drodze tarcia
o atmosferę ziemską, jego prędkości orbitalnej wynoszącej ponad 20 000 km/godz. do prędkości lądowania wynoszącej ok. 200 km/godz., bez ryzyka spłonięcia wskutek nadmiernego tarcia).
Według Morgenthalera
symulować, to znaczy odtworzyć istotę systemu lub jego działanie bez rzeczywistego uruchamiana samego systemu
Naylor (1975) definiuje symulację jako:
technikę numeryczną, służącą do dokonywania eksperymentów na pewnych rodzajach modeli matematycznych, które opisują przy pomocy maszyny cyfrowej (komputerów) zachowanie się złożonego systemu w ciągu długiego okresu czasu
Wybrane elementy definicji Naylora:
CEL SYMULACJI
eksperyment prowadzony na modelu systemu złożonego.
Odcinamy się od problemów trywialnych, (rozwiązywalnych bez uciekania się do symulacji), z drugiej strony podkreślamy wagę układu eksperymentu oraz analizę danych wynikowych.
Wybrane elementy definicji Naylora:
CHARAKTER SYMULACJI
analiza zachowania się systemu w czasie. W zasadzie można eksperymenty prowadzić zarówno w określonej chwili (symulacje przekrojowe), jak i w czasie (symulacje szeregów czasowych).
Wybrane elementy definicji Naylora:
TECHNIKA POSTĘPOWANIA
numeryczna, co może sugerować,
iż symulacja jest techniką ostatniej szansy
i stosowana jest wówczas, gdy nie ma możliwości uzyskania rozwiązania w drodze analitycznej. Jednak w praktyce często okazuje się, że symulacja jest techniką tańszą, prostszą
i mniej pracochłonną oraz wymagającą prostszego oprogramowania komputerowego,
a przy tym znacznie elastyczniejszą.
Rozważmy system ze zmienną wyjściową y, pozostającą w zależności funkcyjnej F (dla uproszczenia przyjmiemy na razie, że jest to funkcja liniowa) od zmiennych xk:
yt = F (x1, x2 ,..., xK )=b1x1 + b2x2 +...+ bKxK dla k=1, ..,K)
yt - nazywana jest reakcją
x1, x2 ,..., xK - to bodźce (czynniki)
F - opisuje powierzchnię reakcji
W eksperymencie kontrolowanym zmieniamy wartości x, aby obserwować reakcję y. Daje to możność zgromadzenia próby liczącej T obserwacji na y oraz x. Na podstawie zgromadzonych obserwacji możemy oszacować parametry bk powierzchni reakcji, otrzymując model:
yt = F (x1, x2 ,..., xK )=b1x1 + b2x2 +...+ bKxK (sprawdzić i poprawić na podstawie prezętacji)
który można poddawać dalszej interpretacji i analizie.
W sytuacji, gdy eksperyment kontrolowany jest kosztowny lub wręcz niemożliwy, uciekamy się do symulacji traktowanej jako quasi-eksperyment (eksperyment na modelu systemu), w którym zmianie ulegają parametry bk, zmienne xk, lub jedne i drugie.
W wielu eksperymentach pojawia się konieczność uwzględnienia źródeł niepewności w zachowaniu
modelowanego systemu. Stwarza to zapotrzebowanie na wprowadzenie do modelu wielkości przybierających wartości losowe zgodnie z pewnym rozkładem prawdopodobieństw
Przez metodę Monte Carlo rozumie się technikę wyboru wielkości losowych z pewnego rozkładu prawdopodobieństwa -
jest to symulacja stochastyczna
Pojęcie symulacja stochastyczna używane jest
w odniesieniu do eksperymentów typu próbkowanie modelu (model sampling), służących badaniu
właściwości modelu.
Metoda Monte Carlo: we fragmenty modelu (parametry, zmienne, ograniczenia), stanowiące źródło niepewności, wstawiane są zaburzenia wylosowane
z odpowiedniego rozkładu prawdopodobieństwa,
a następnie wyznaczane jest rozwiązanie modelu.
Pojedyncze rozwiązanie otrzymane po wstawieniu wartości konkretnych zaburzeń nazywamy replikacją.
Operacja ta powtarzana jest N-krotnie dając próbę zawierającą N replikacji.
Symulacja stochastyczna rozumiana jako próbkowanie modelu, oznacza generowanie reprezentatywnej próby zmiennych niezależnych (egzogenicznych) modelu,
aby następnie wyliczyć pewne sumaryczne charakterystyki trajektorii, po jakiej biegną zmienne zależne (endogeniczne) modelu.
Próbkowanie modelu pozwala na określenie charakteru rozkładów wynikowych tam, gdzie zastosowanie technik analitycznych jest zawodne.
Symulacja dynamiczna a statyczna
Słowo dynamiczny używane jest
w dwóch podstawowych znaczeniach:
żywy, szybko zmieniający się
w czasie, jako przeciwieństwo powolnego, oraz
zależny od swojej przeszłości , jako przeciwieństwo statycznego.
System dynamiczny (zależny od swojej przeszłości) to system z pamięcią albo mający stan, w przeciwieństwie do systemu statycznego (bez pamięci).
W odróżnieniu od systemu statycznego, system dynamiczny poddany dwukrotnie oddziaływaniu takich samych bodźców zewnętrznych może zareagować odmiennie, zależnie od swojego stanu (zawartego w pamięci).
Jednym z typowych przykładów systemu dynamicznego jest system sterowania zapasami.
Symulacja zdarzeń dyskretnych
W pierwszym przykładzie opisujemy przypadek elementarny statyczny, dający się rozwiązać również przez fizycznie przeprowadzony eksperyment.
Przykład ten służy do wprowadzenia podstawowych pojęć i mechanizmów losowania.
Przykład: produkcja rurek
Pewien rzemieślnik dysponuje specjalistyczną aparaturą pozwalającą na łączenie rurek złotych z platynowymi.
Warunki planowanego kontraktu z NASA na dostawę rurek spojonych pozwalają na pomiar długości elementów
z dokładnością do 1 mm.
Kontrola techniczna dostawcy rurek złotych odrzuca rurki krótsze niż 20 mm lub dłuższe niż 25 mm.
Kontrola techniczna dostawcy rurek platynowych odrzuca rurki krótsze niż 5 mm lub dłuższe niż 8 mm.
Do łączenia rurki dobierane są losowo.
Kontrakt będzie dla rzemieślnika opłacalny, jeśli co najmniej połowa
z połączonych rurek będzie miała długość 29, 30 lub 31 mm.
Po przebadaniu większej partii rurek platynowych rzemieślnik stwierdził:
Czy rzemieślnikowi opłaca się podpisać kontrakt?
Dokonujemy prostych obliczeń statystycznych
Wyznaczamy parametry rozkładu wynikowego w populacji generalnej:
Zazwyczaj jednak nie posiadamy informacji o populacji generalnej,
szukamy więc innych sposobów zdobycia wiedzy o parametrach rozkładu interesujących nas zmiennych.
Rozwiązanie praktyczne - eksperyment fizyczny
W praktyce możemy oszacować podstawowe parametry rozkładu połączonej rurki, tj. średnią długość rurki oraz rozproszenie tej długości uruchamiając proces produkcyjny, tj. wykonać następujące kroki:
pobrać rurkę złotą i pomierzyć jej długość DRZ,
pobrać rurkę platynową i pomierzyć jej długość DRP,
obliczyć długość rurki spojonej DRS sumując długości rurek składowych, zwrócić pomierzone rurki do pojemników z których je wylosowano,
N razy powtórzyć kroki 1-3, każda powtórka (replikacja) dostarcza kolejnej obserwacji na zmiennych DRZ, DRP oraz DRS,
wyliczyć parametry rozkładu rurki spojonej: średnią jej długość oraz rozproszenie, na podstawie N replikacjiPostępowanie takie wygeneruje N elementową losową próbę połączonych rurek. Z warunków zadania wynika, że do kolejnych replikacji rurki losowane są niezależnie, każda z populacji
o rozkładzie częstości niezmiennym w każdym losowaniu.
W tej sytuacji z centralnego twierdzenia granicznego Lindeberga -Levy'ego wynika, że średnia długość rurki w próbie jest zgodnym estymatorem średniej długości rurki w populacji generalnej, odchylenie standardowe w próbie jest zgodnym estymatorem odchylenia standardowego długości w populacji generalnej.
Stwarza to podstawy do uogólnienia na parametry populacji generalnej wniosków wyciągniętych na podstawie dokonanych
w próbie pomiarów.
Symulacja prosta
Główną niedoskonałością rozwiązania praktycznego jest to,
że wymaga ono fizycznego losowania rurek - składników z odpowiednich pojemników. Jest to operacja kłopotliwa, a przy wielokrotnym powtarzaniu - pracochłonna i kosztowna.
Z opisu eksperymentu fizycznego wynika jednak, że wcale nie musimy losować fizycznie rurek. Wystarczy bowiem losować wartość zmiennej DRP (długość rurki platynowej) oraz zmiennej DRZ (długość rurki złotej).
Istotne jest, aby rozkłady prawdopodobieństwa losowanych zmiennych pokrywały się z odpowiadającymi rozkładami
w populacji generalnej
(mówimy, że zmienne DRZ i DRP są losowane z tych rozkładów). Każda powtórka losowania (replikacja) dostarcza kolejnej obserwacji na zmiennych DRZ, DRP oraz DRS (długość rurki spojonej).
Losowanie metodą odwracania dystrybuant
Rozważmy zagadnienie losowania długości rurki złotej w taki sposób, aby określone długości rurek pojawiały się w naszej próbie z częstością, równą stwierdzonemu prawdopodobieństwu.
Zajmijmy się więc możliwością losowania wartości zmiennej DRZ, (a następnie DRP) w sposób matematyczny, bez aktu fizycznego losowania, tak:
aby długość 21 pojawiała się 5 razy na sto ......... itd..
Losowanie metodą odwracania dystrybuanty
Do losowania długości rurek z odpowiednich rozkładów będzie nam potrzebna zmienna przyjmująca z jednakową szansą wartości z przedziału (0,1), tj. zmienna o rozkładzie równomiernym (zwanym też rozkładem jednostajnym) na odcinku (0,1).
Oto przykładowe realizacje takiej zmiennej. Nazwiemy ja zmienną losującą
i oznaczymy symbolem U.
Losowanie metodą odwracania dystrybuanty
Przyjmijmy zasadę, że:
jeśli zmienna losująca U ma wartość nie większą od 0,05, oznacza to wylosowanie rurki złotej o długości 21 mm; w przeciwnym razie
jeśli U ma wartość nie większą od 0,30 - wylosowano rurkę o długości
22 mm; w przeciwnym raziejeśli U ma wartość nie większą od 0,75 - wylosowano rurkę o długości
23 mm; w przeciwnym raziejeśli U ma wartość nie większą od 0,90 - wylosowano rurkę o długości
24 mm; w przeciwnym raziewylosowano rurkę 25 mm.
Losowanie metodą odwracania dystrybuanty
Tak otrzymana próba podlega opracowaniu statystycznemu - stosownie do potrzeb.
Tradycyjnie do podsumowań wyznaczane są miary klasyczne oparte na momentach rozkładu zmiennych, takie jak: średnia opisująca lokalizację centrum rozkładu, wariancja opisująca jego rozproszenie, czasem również miary asymetrii oraz kurtozy
Jeśli będziemy zwiększali liczbę replikacji, to częstość przypadków, w których zmienna losująca mająca rozkład równomierny trafi do wybranego przedziału, będzie coraz bliższa udziałów długości tego przedziału w odcinku (0,1]. Zatem w dużej liczbie replikacji
związana z tym przedziałem długość rurki pojawi się w próbie z częstością proporcjonalną do tego udziału. Możemy wygenerować dowolnie wielką liczbę replikacji, ograniczoną jedynie względami praktycznymi.
Wykonanie 1000 replikacji
W naszym przypadku średnia długość rurki wynosi 30,008 mm, zaś odchylenie standardowe 1,3303.
Jeśli rozkład długości rurki byłby normalny, należałoby się spodziewać, że w przedziale (30,008 - 1,3303; 30,008 + 1,3303) tj. (28,667;31,338) znajdzie się ok. 68% rurek.
Dla rzemieślnika może to być informacja zadowalająca
Z punktu widzenia rzemieślnika cenniejszej informacji dostarczą mu miary pozycyjne takie jak np. kwartyle. Pierwszy kwartyl wynosi 29 mm, zaś trzeci kwartyl - 31 mm, zatem co najmniej
50% rurek ma długość zawartą pomiędzy tymi wartościami. Rzemieślnik może stąd wnioskować o opłacalności kontraktu
Wykonanie 1000 replikacji
Dostosowując technikę opracowania wyników symulacji do kluczowego dla rzemieślnika pytania: ile - moglibyśmy pominąć wyznaczanie takich parametrów rozkładu długości rurki, jak średnia, czy odchylenie standardowe, ograniczając analizę do zliczenia ilości rurek o długości 29-31 mm i wyliczenia procentu rurek spełniających warunki kontraktu.
Widzimy, że aż 76,00% rurek spełnia te warunki. Nawet, jeżeli wyniki te są obarczone zmiennością z próby, wygląda na to,
że rzemieślnik ma spory zapas bezpieczeństwa.
WNIOSKI RZEMIEŚLNIKA
W naszym przykładzie najlepsza metoda opracowania wyników symulacji polega na tym, aby rzemieślnik rozważył, ile spojonych rurek wpada do przedziału [29,31] dopuszczalnego z punktu widzenia odbiorcy,
a w konsekwencji, jakie koszty poniesie na wyprodukowanie rurek odrzuconych.
Jeśli koszty te okażą się nieakceptowalne, rzemieślnik może odstąpić od podpisania kontraktu.
Symulacja w konwencji
CZAS NASTĘPNEGO ZDARZENIA
W symulacji dynamicznej pojawiają się elementy charakteryzujące czas pojawienia się następnego zdarzenia: np. czas realizacji zamówienia na kolejną dostawę towaru; pozostałe elementy modelu działały
w konwencji wymagającej cięcia czasu na plasterki.
Przez zdarzenie rozumiemy zmianę stanu systemu,
w szczególności zmianę wartości zmiennej modelu innej, niż zmienna Czas.
Pakiet EXCEL nie najlepiej nadaje się do zainstalowania w nim modelu w konwencji następne zdarzenie. Specjalistyczne pakiety symulacyjne, dostosowane do takich zadań, składają się w zasadzie z trzech typowych elementów składowych: wykonawcy, modelu oraz procedur pomocniczych (generatory rozkładów, wykresów i tabel, procedury statystyczne).
Terminologia modeli zdarzeń dyskretnych
W symulowanych systemach występują dwa rodzaje elementów (obiektów): jednostki (entities) działające w systemie oraz zasoby (resources).
Jednostki są indywidualnymi elementami działającymi
w systemie i ich zachowanie jest przedmiotem symulacji. Zachowanie każdej jednostki jest bezpośrednio śledzone,
a zmiana jej stanu - rejestrowana (np. jednostka pacjent udający się do przychodni zmienia swój stan: idzie na przystanek, oczekuje na autobus, jedzie autobusem etc.) Zmiana stanu całego systemu jest owocem wzajemnych oddziaływań jednostek funkcjonujących w tym systemie. Jednostki mogą być permanentne (funkcjonują w modelu od początku do końca symulacji) lub czasowe (pojawiają się i znikają w miarę potrzeb).
Zasoby są takimi elementami systemu, które nie są modelowane indywidualnie, ale zmieniają się wskutek działania jednostek (np. liczba pasażerów oczekujących na przystanku).
Elementy składowe zasobu są jednorodne
i przeliczalne, a wykonawca rejestruje wielkość (liczebność) zasobu.
Zaliczenie elementu systemu do grupy jednostek lub zasobów jest decyzją twórcy modelu, wyznaczoną przez: cel symulacji, rodzaj modelu i jego szczegółowość.
Jednostki mogą być grupowane w klasy (stałe grupy identycznych jednostek), zbiory (czasowe grupy jednostek), a także mogą być rozróżniane według atrybutów (cech).
Upływ czasu znaczony jest przez:
• zdarzenia (events) — momenty, w których zaszła istotna zmiana stanu systemu (gdy np. jednostka opuszcza jakiś zbiór, jakaś czynność rozpoczyna się lub kończy);
• czynności (activities) - gdy jakaś jednostka przechodzi ze zbioru do zbioru dzięki operacji, w której uczestniczy; czynności są rozpoczynane zdarzeniami przekształcającymi stan systemu;
• procesy - chronologicznie uporządkowane ciągi zdarzeń, tudzież czynności, rozpoczynanych i kończonych zdarzeniami;
• zegar - zmienna reprezentująca moment, w którym znajduje się symulowany system, zmiany zegara symulują upływ czasu.
Rodzaje zdarzeń dyskretnych
(w konwencji CZAS NASTĘPNEGO ZDARZENIA)
Zdarzenia dyskretne dzieli się na:
bezwarunkowe B (bound), tj. takie, których pojawienie da się przewidzieć,
warunkowe W (w oryginale C od conditio-nal albo cooperative) tj. takie, których pojawienie jest uwarunkowane, zwykle dostępnością pewnego zasobu.
Trzy fazy symulacji
(w konwencji CZAS NASTĘPNEGO ZDARZENIA)
Każdej jednostce modelu przypisany jest PakietTrzech przechowujący następujące trzy informacje o jednostce:
1) Termin - zawiera informację o momencie najbliższej zmiany stanu;
2) NastępneZdarzenie - zawiera informacje o tym, jakie zdarzenie bezwarunkowe ma zajść w momencie Termin;
3) Gotowość - zawiera informacje logiczną Prawda (wówczas zawartość komórek Termin oraz NastępneZdarzenie nie ma sensu), gdy jednostka nie jest zaangażowana w czynność kończącą się zdarzeniem bezwarunkowym, w przeciwnym razie komórka zawiera informację Falsz.
Wykonawca zarządza jednostkami, analizując i modyfikując informacje zawartą w PakiecieTrzech.
Symulacja realizowana jest w przedziale czasowym (mpocz,mkon) przez powtarzania trzech faz: A, B i C:
Faza A: SprawdźKalendarz
Wykonawca poszukuje w kalendarzu nadciągającego (najbliższego zapisanego) zdarzenia i przestawia Zegar symulacji na termin tego zdarzenia; kolejne przesunięcie zegara odbędzie się dopiero w następnej fazie A.
Faza B: Wykonaj
Wykonawca przegląda jednostki na liście DoWykonania i dla każdej jednostki z tej listy wykonuje trzy operacje:
1) w PakiecieTrzech tej jednostki zmienia zawartość komórki Gotowy na Prawda,
2) realizuje zawartość komórki NastępneZdarzenie,
3) usuwa jednostkę z listy DoWykonania.
Faza C: PróbujWszystkie W
Wykonawca wykonuje po kolei wszystkie testy rozpoczęcia czynności i uruchamia te czynności, dla których warunek rozpoczęcia jest spełniony.
Symulacja MODELI CIĄGŁYCH
Symulacja modeli ekonometrycznych jest szczególnie
rozwiniętą, wyspecjalizowaną gałęzią symulacji.
W kontekście modeli wielorównaniowych słowo symulacja używane jest zarówno jako określenie procesu rozwiązywania modelu (symulacja deterministyczna), jak i procesu badania właściwości estymatorów, testów lub rozwiązań modelu (symulacja stochastyczna).
Rozróżniamy symulację (czynność) od rozwiązania (produktu tej czynności). Rozwiązanie dla kilku okresów czasu daje trajektorie, po której biegną zmienne endogeniczne. Symulacja dynamiczna różni się od statycznej sposobem, w jaki traktujemy opóźnione zmienne endogeniczne występujące po prawej stronie znaku równości: w dynamicznej wstawiamy tam rozwiązania wyliczone w poprzednich okresach, w statycznej wstawiamy tam empiryczne wartości zmiennych endogenicznych; musimy je zatem znać
Testowanie hipotez dotyczących wartości parametrów strukturalnych
W praktyce wykorzystuje się fakt, że stosunek:
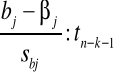
ma rozkład t Studenta o (n-k-1) stopniach swobody
Zmienna losowa X typu ciągłego ma rozkład
t Studenta o n stopniach swobody, jeżeli jej gęstość f wyraża się wzorem:
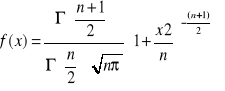
Rozkład t Studenta o n stopniach swobody
Testowanie hipotez dotyczących wartości parametrów strukturalnych (c.d.)
Przypuszcza się, że parametr strukturalny bj (j=0,1..,k) przyjmuje pewna ustaloną wartość
W sposób formalny przypuszczenie to może być zapisane jako hipoteza zerowa:
![]()
![]()
wobec hipotezy alternatywnej:
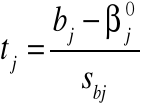
Jeśli obliczony (lub odczytany z tablic) poziom istotności pj dla:
jest Ł 0,05
mamy podstawy do odrzucenia H0 czyli dane parametr xj istotnie oddziałuje na cechę objaśnianą
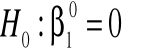
Postawmy hipotezę zerową, że:
Ostatecznie
Wszystkie wzory i zdjęcie należy sprawdzić z prezentacją ponieważ nie udało mi się ich w 100% przekopiować.
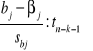
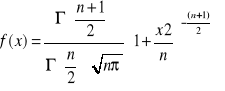
![]()
![]()
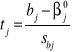
![]()
Wyszukiwarka
Podobne podstrony:
prognozowanie i symulacje wyklad (25 str)
Program - PROGNOZOWANIE I SYMULACJA, STUDIA, prognozowanie
prognozowanie i symulacje
Prognozowanie i symulacje wykład 1 2010
prognozowanie i symulacje-ściąga, Ekonomia
PROGNOZOWANIE I SYMULACJE wykłady
Prognozowanie i symulacje materialy
Ściąga prognozowanie i symulacje, Szkoła, EKONOMIA, EKONOMIA MATEMATYCZNA
inf 3, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH i UW), prognozowanie i symulacje
TEST na egzamin z rozwiazaniami, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH i UW), prognozowanie i symul
Prognozy i symulacje testy
Prognozowanie i symulacje(1)
prognozowanie i symulacje międzynarodowe XMLUTYOVCYVJQZOM7KBZKDMOORHTDBRS3ZQ4W4Q
Progn i sym 2004 lato, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH i UW), prognozowanie i symulacje
W firmie sprzedającej komputery wyznaczono następujący trend, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH
Prognozy i symulacje (17 stron) RE5NCEJ42LIWYV7LXE57UBDEZZZE3W7KIT6DZFQ
Prognozowanie i symulacje miedz skrypt z 2011 roku id 394821
zagadnienia prognozowanie, Prognozowanie i Symulacje
więcej podobnych podstron