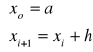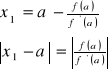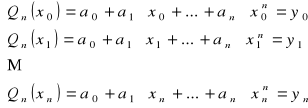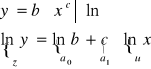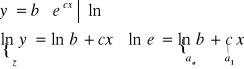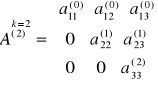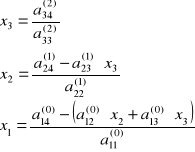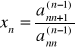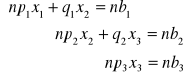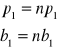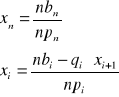1.Całkowanie funkcji metodą prostokątów.

a) przedstawić na rysunku sposób postępowania w tej metodzie

Korzysta się z węzłów równoległych. Dzielimy przedział [a,b] na `h' podprzedziałów o jednakowej długości.

h-odległość między poszczególnymi węzłami, np.: x₀, x₁, x₂ to h=2→ostatnia liczba ciągu,

n+1→liczba wyrazów w ciągu,

x₀, x₁, x₂,..., x_n→zapis ciągu w postaci x_i, i=0,1,...,n; n-oznacza liczbę przedziałów

dane: a,b,h

Metoda 1:

x_i=a+i⋅h

x₀=a

x₁=a+h

x₂=a+2h

Metoda 2:

x₁=x₀+h

x₂=x₁+h

szukane: x=?

i=0,1,2,...,n

i=0,1,2,...,n-1

b)podać wyprowadzenie oraz ostateczny wzór na przybliżoną wartość całki

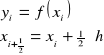
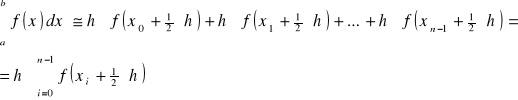
2.Całkowanie funkcji metodą trapezów.

a) przedstawić na rysunku sposób postępowania w tej metodzie

Metoda ta jest dokładniejsza od metody prostokątów. Podział na przedziały i wyznaczanie węzłów jak w metodzie prostokątów. Pole pod krzywą zastępujemy trapezami.

b)podać wyprowadzenie oraz ostateczny wzór na przybliżoną wartość całki

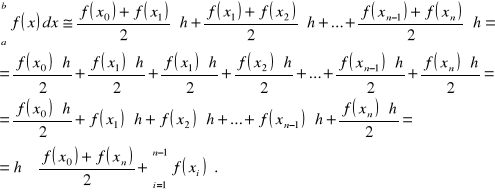
3.Rozwiązanie równania nieliniowego metodą połowicznego podziału

a)podać przykład równania nieliniowego:
.

b)określić niewiadomą:

c)przedstawić na rysunku sposób poszukiwania niewiadomej

d)podać warunki, jakie musi spełniać funkcja występująca w równaniu

dane: [a₀,b₀]; f(a₀)⋅ f(b₀)<0; istnieje rzeczywisty i jednokrotny pierwiastek równania

założenie: f(x) jest ciągła na przedziale [a₀,b₀]

e)co należy przyjąć, aby rozpocząć wyznaczanie rozwiązania

Należy przyjąć przedział [a, b], na którego końcach wartości funkcji f(x) mają przeciwne znaki: f(a₀)⋅ f(b₀)<0.

Ewentualnie można przyjąć ε jako dokładność, z jaką będziemy szukać miejsca zerowego funkcji.

f)jak wyznacza się kolejne przybliżenia rozwiązania

Wzór metody:

1. Ustalenie przedziału [a_i, b_i]; f(a_i)⋅ f(b_i)<0

2.
jest to początkowe przybliżenie rozwiązania

3.
wtedy x_i-jest rozwiązaniem (gdzie: ε-liczba mała dodatnia)

gdy:
liczymy dalej, ustalamy przedział:

[a_i+1, b_i+1]=[a_i,x_i], f(a_i)⋅f(x_i)<0

[x_i,b_i], f(x_i)⋅f(b_i)>0

Jeżeli funkcja jest bardzo stroma to sprawdza się tez drugi warunek:

4.
wtedy x_i jest rozwiązaniem,

gdy:
liczymy dale, wracamy do punktu 3.

g)jaki jest warunek kończący proces iteracyjny

Proces iteracji kończymy, gdy:
, wtedy x_i jest rozwiązaniem,

lub gdy
wtedy x_i+1 jest rozwiązaniem.

4.Rozwiązanie równania nieliniowego metodą Newtona (metoda stycznych)

a)podać przykład równania nieliniowego:
.

b)określić niewiadomą:

c)przedstawić na rysunku sposób poszukiwania niewiadomej

d)podać warunki, jakie musi spełniać funkcja występująca w równaniu

f '(x)≠0 f ''(x)≠0

V x∈U(x^*)

e)co należy przyjąć, aby rozpocząć wyznaczanie rozwiązania

założenia:

nie zmienia znaku w przedziale [a,b]

teza:

proces iteracyjny metody Newton'a jest zbieżny do x^*

punkt x1 znalazł się we wnętrzu przedziału

f)jak wyznacza się kolejne przybliżenia rozwiązania

--prowadzimy styczną do f(x) w punkcie (x₀, f(x₀))

--w miejscu przecięcia się stycznej z osią OX otrzymujemy punkt x₁, który jest pierwszym przybliżeniem,

--znajdujemy wartość funkcji dla punktu x₁,

--z punktu o współrzędnych (x₁,f(x₁)) prowadzimy styczną do f(x),

--w miejscu przecięcia się stycznej z osią OX otrzymujemy punkt x₂, który jest drugim przybliżeniem, i tak aż do znalezienia miejsca zerowego.

Równanie ogóle prostej: y=ax+b; a=f'(x₀)

--dla stycznej w punkcie x₀:

y=f'(x₀)⋅x+b

y₀=f'(x₀)⋅x₀+b⇒b=y₀- f'(x₀)⋅x₀

y=f'(x₀)⋅x+y₀-f'(x₀)⋅x₀-równanie prostej stycznej w punkcie x₀ do krzywej f(x)

Szukamy wartości punktu x₁:

0=f'(x₀)⋅x₁+y₀-f'(x₀)⋅x₀

-f'(x₀)⋅x₁= y₀-f'(x₀)⋅x₀ /: (-f'(x₀))

y₀=f(x₀)

wzór Newton'a na I przybliżenie gdy znane jest x₀.

Algorytm metody:

1.przyjmujemy x₀-przybliżenie początkowego rozwiązania, ε1, ε2

2. f(x_i)<ε1

⇒T: x_i-rozwiązanie

⇒N: pkt.3.

3.

4.

⇒T: x_i+1-rozwiązanie

⇒N: powrót do pkt.2.

g)jaki jest warunek kończący proces iteracyjny

Proces iteracji kończymy, gdy: f(x_i)<ε1, wtedy x_i jest rozw.,

lub gdy
wtedy x_i+1 jest rozwiązaniem.

5.Interpolacja funkcji za pomocą wielomianu Lagrange'a

a)napisać jaki jest cel interpolowania funkcji (co jest dane, co obliczamy, przy użyciu jakiego warunku)

Celem interpolacji funkcji za pomocą wielomianu Lagrange'a jest znalezienie wzoru funkcji ciągłej f(x) interpolującej funkcję w postaci dyskretnej y(x).

Dane:

x0,x1,...,xn-węzły interpolacyjne (nie są równo odległe) y0,y1,...,yn-wartości funkcji interpolowanej

funkcja w postaci dyskretnej

Szukane: funkcja w postaci ciągłej f(x) interpolująca funkcję y(x) tak, aby f(x) był wielomianem
, k-stopień wielomianu

Funkcja interpolująca musi spełniać warunek: 1.f(xi)=yi 2.f(x)-wielomian.

b)przedstawić ogólną postać wielomianu Lagrange'a

a₀, a₁-niewiadome w wielomianie,

n+1-liczba węzłów interpolacyjnych.

c)podać postać układu równań, z którego wyznaczane są współczynniki wielomianu

n+1-niewiadomych n+1-równań

d)napisać wzór wielomianu Lagrange'a

Rozpisany wielomian Lagrange'a:

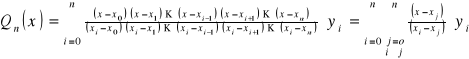
e)określić w jakich przypadkach nie należy używać wielomianu Lagrange'a i dlaczego

Wielomianu Lagrane'a nie należy używać przy dużej liczbie węzłów równoodległych.

Zdarza się, że w pobliżu końców wielomian Lagrange'a oscyluje (zjawisko Rungego).

Aby je wyeliminować posługujemy się interpolację za pomocą funkcji sklejanych.

6.Interpolacja funkcji za pomocą funkcji sklejanej z wielomianów stopnia pierwszego

a)napisać jaki jest cel interpolowania funkcji (co jest dane, co obliczamy, przy użyciu jakiego warunku)

Celem interpolacji funkcji z pomocą funkcji sklejanej jest znalezienie wzoru funkcji sklejanej Skl(x) interpolującej funkcję daną w postaci dyskretnej y(x).

Dane:

x0,x1,...,xn-węzły interpolacyjne y0,y1,...,yn-wartości funkcji interpolowanej

funkcja w postaci dyskretnej

Szukane: Skl(x)-funkcja interpolująca

Warunek:

b)napisać jaka jest ogólna postać funkcji sklejanej z wielomianów stopnia pierwszego

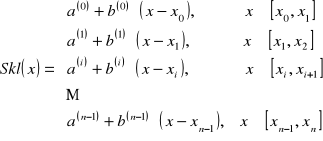
wartości w nawiasach w indeksie górnym przy „a” i „b” nie oznaczają potęgi !!!

c)wypisać wszystkie parametry funkcji sklejanej

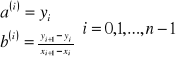
d)podać warunki, których spełnienie gwarantuje wyznaczenie parametrów funkcji sklejanej oraz opisać sposób wyznaczenia parametrów

Parametry a⁽ⁱ⁾ wyznaczamy:

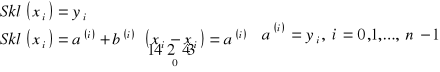
Parametry b⁽ⁱ⁾ wyznaczamy:

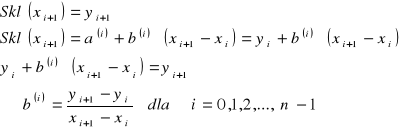
7.Aproksymacja funkcji, za pomocą funkcji potęgowej.

a)jaki jest cel aproksymacji (co jest dane, a co obliczamy, przy użyciu jakiego warunku),

Celem aproksymacji jest znalezienie funkcji jak najlepiej opisującej układ punktów na płaszczyźnie.

Możemy aproksymować linią prostą (najczęściej), wykładniczą, logarytmiczną.

Aproksymację potęgową sprowadzamy do aproksymacji liniowej.

Aproksymacja funkcji (przybliżanie, zastępowanie)

Dane:

x0,x1,...,xn y0,y1,...,yn

z pomiarów

Szukane:

f(x) - najlepiej przybliżająca tą zależność

f(x)=b⋅x^c

Warunek:

Wielomian I-go stopnia:

Parametry będą najlepsze, gdy:
i
, bo suma kwadratów jest min.

a_o, a₁ - niewiadome, mamy wybrać najlepsze parametry (gdy suma kwadratów odchyłek będzie min.).

b)jak sprowadza się podane zadanie, do zagadnienia aproksymacji za pomocą wielomianu stopnia pierwszego,

sprowadzenie do zależności liniowej

- funkcja liniowa

Obliczamy a_o i a₁, a następnie obliczamy b i c:

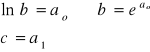
I otrzymujemy wzór funkcji: y=b⋅x^c.

c)jak powstaje i jaką ma postać układ równań, z którego wyznacza się parametry wielomianu

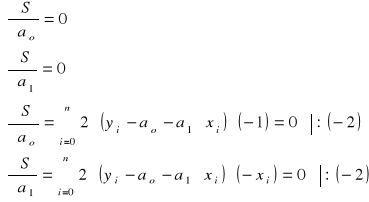
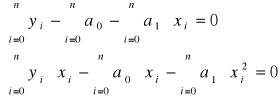
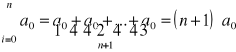
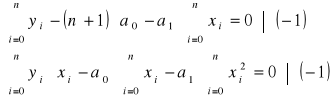
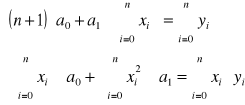
Układ równań rozwiązać metodą wyznaczników:

.

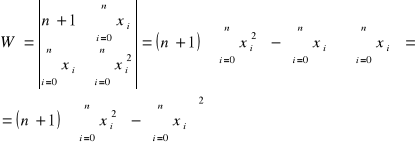
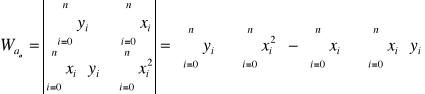
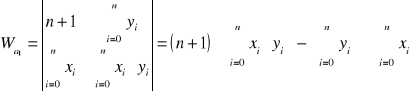
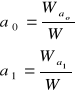
8.Aproksymacja funkcji, za pomocą funkcji wykładniczej

a)jaki jest cel aproksymacji (co jest dane, a co obliczamy, przy użyciu jakiego warunku),

Celem aproksymacji jest znalezienie funkcji jak najlepiej opisującej układ punktów na płaszczyźnie.

Możemy aproksymować linią prostą (najczęściej), wykładniczą, logarytmiczną.

Aproksymację potęgową sprowadzamy do aproksymacji liniowej.

Aproksymacja funkcji (przybliżanie, zastępowanie)

Dane:

x0,x1,...,xn y0,y1,...,yn

z pomiarów

Szukane:

f(x) - najlepiej przybliżająca tą zależność

f(x)=b⋅e^cx

Warunek:

Wielomian I-go stopnia:

Parametry będą najlepsze, gdy:
i
, bo suma kwadratów jest min.

a_o, a₁ - niewiadome, mamy wybrać najlepsze parametry (gdy suma kwadratów odchyłek będzie min.).

b)jak sprowadza się podane zadanie, do zagadnienia aproksymacji za pomocą wielomianu stopnia pierwszego,

sprowadzenie do zależności liniowej

- funkcja liniowa

Obliczamy a_o i a₁, a następnie obliczamy b i c:

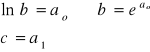
I otrzymujemy wzór funkcji: y=b⋅e^cx.

c)jak powstaje i jaką ma postać układ równań, z którego wyznacza się parametry wielomianu

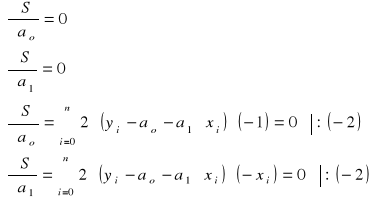
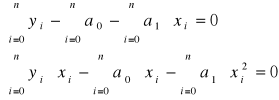
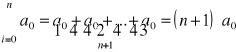
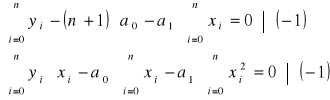
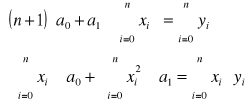
Układ równań rozwiązać metodą wyznaczników:

.

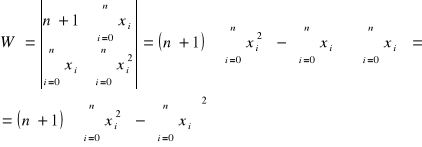
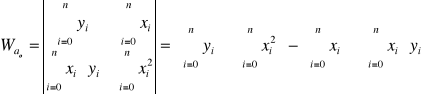
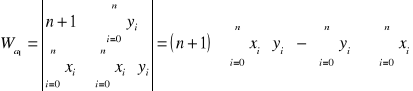
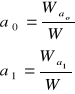
9.Rozwiązanie zagadnienia początkowego metodą Eulera.

a) podać przykład zagadnienia początkowego,

lub

b) określić niewiadomą, przedział w którym jest wyznaczana, postać rozwiązania,

y(x) - niewiadoma w przedziale [a, b]

jako rozwiązanie dostajemy funkcję w postaci dyskretnej, w punktach x₁, x₂ … x_n znajdujemy przybliżone wartości (rozwiązanie dyskretne)

wprowadzamy oznaczenie w_i'= f(x_i, w_i)

współczynnik kierunkowy stycznej = pochodnej funkcji w punkcie

c) w jakich punktach przedziału i w jakiej kolejności, wyznaczane są wartości niewiadomej,

aby znaleźć rozwiązanie dzielimy przedział [a, b] na n pod przedziałów równoległych

metoda Eulera:

w₁ = α +h ⋅ f(x_o, w_o)

w'(x₁)=f (x₁,w₁)

w₂ = w₁ +h ⋅ f(x_1,w₁)

i =1,2,3…

Z: w_o = y_o w_o - warunek początkowy

d) przy użyciu jakiego wzoru wyznaczane są wartości niewiadomej

w_i+1 - kolejna wartość funkcji

w_i - poprzednia wartość funkcji

h - długość przedziału między węzłami

f(x_i, w_i) - przybliżona wartość funkcji

10. Rozwiązanie zagadnienia początkowego metodą Rungego - Kutty II-go rzędu.

a) podać przykład zagadnienia początkowego

postać ogólna:

y(a) =   warunek początkowy

przykład:

y(1) =   6

b) określić niewiadomą, przedział w którym jest wyznaczana, postać rozwiązania

niewiadoma to: y(x)

Wyznaczamy ją w przedziale [a, b]

c) w jakich punktach przedziału i w jakiej kolejności, wyznaczane są wartości niewiadomej,

Wyprowadzenie wzoru:

w1 = w0 + h* f (x0 + ½*h , w0 + ½ * h * f (x0, w0))

w _{i +1} = w _i + h * f (x _i + ½*h, w _i + ½ * h * f (x _i , w _i)) i = 0,1, ... , n-1

k1 = * h * f (x _i , w _i)

k2 = h * f (x _i + ½*h, w _i + ½ * h * f (x _i , w _i))

d) przy użyciu jakiego wzoru wyznaczane są wartości niewiadomej

w _{i +1} = w _i + h * f (x _i + ½*h, w _i + ½ * h * f (x _i , w _i)) i = 0,1, ... , n-1

h - długość przedziału, na które dzielimy obszar, w którym szukamy rozwiązań

w _i - wartość funkcji w punkcie poprzednim

11. Rozwiązywanie układu równań liniowych metodą Gaussa

a) napisać ogólną postać rozwiązywanego układu równań oraz jego formę macierzową

b - wektor wyrazów wolnych A - macierz układu utworzona tylko ze współczynników przy niewiadomych x - wektor niewiadomych

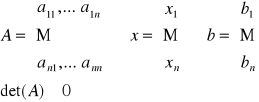
układ ma rozwiązani jednoznaczne

b) narysować macierz układu

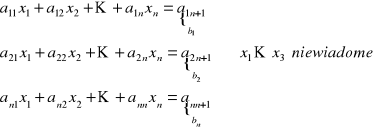
c) określić czym jest niewiadoma

Niewiadoma jest wektorem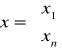

d) napisać co to znaczy, że układ jest źle uwarunkowany i w jaki sposób ocenia się uwarunkowanie układu

Jeżeli w min. sposób zmienimy wartość współczynników to spowodujemy zasadniczą zmianę rozwiązania układu. Taki układ nazywamy układem źle uwarunkowanym. Tak może się stać gdy det(A)≠0, ale detA≈0

e) opisać słowami na czym polega metoda

Metoda ta polega na eliminacji kolejnych zmiennych z kolejnych równań (poza pierwszym) przez przekształcanie macierzy współczynników równania w kolejnych przekształceniach tak, by doprowadzić do macierzy trójkątnej górnej.

f) na przykładzie 3 równań o 3 niewiadomych przedstawić dwa pierwsze etapy eliminacji niewiadomych

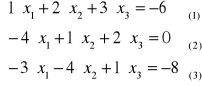
I etap z (2) i (3) eliminujemy x₁

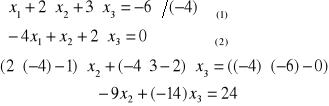
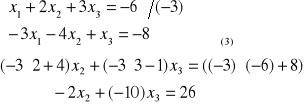
po I etapie:

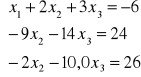
II etap eliminujemy x₂ z (3)

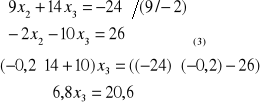
g) narysować macierz układu po ostatnim etapie eliminacji niewiadomych

mamy po II etapie:

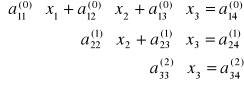
czyli:

Macierz trójkątna górna k = 1, … n-1 i = k+1, … n j = k+1, … n

h) wyjaśnić na czym polega postępowanie odwrotne

Polega na wyliczaniu kolejnych niewiadomych od tyłu od największego.

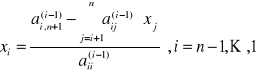
12. Rozwiązywanie układu równań liniowych metodą Thomasa.

a) napisać ogólną postać rozwiązywanego układu równań oraz jego formę macierzową

b - wektor wyrazów wolnych A - macierz układu utworzona tylko ze współczynników przy niewiadomych x - wektor niewiadomych

b) narysować macierz układu

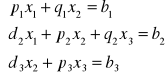
c) określić czym jest niewiadoma

Niewiadoma jest wektorem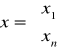

d) napisać co to znaczy, że układ jest źle uwarunkowany i w jaki sposób ocenia się uwarunkowanie układu

Jeżeli w min. sposób zmienimy wartość współczynników to spowodujemy zasadniczą zmianę rozwiązania układu. Taki układ nazywamy układem źle uwarunkowanym.

e) opisać słowami na czym polega metoda

Metoda ta polega na eliminacji kolejnych zmiennych z kolejnych równań (poza pierwszym) przez przekształcanie macierzy współczynników równania w kolejnych przekształceniach

f) na przykładzie 3 równań o 3 niewiadomych przedstawić dwa pierwsze etapy eliminacji niewiadomych

jak chcecie to przykład możecie sami Sobie wklepać ja już się wypisuje z tego …

g) narysować macierz układu po ostatnim etapie eliminacji niewiadomych

czyli mamy:

h) wyjaśnić na czym polega postępowanie odwrotne

13. Rozwiązanie zagadnienia początkowo - brzegowego, z równaniem różniczkowym typu parabolicznego, przy użyciu schematu 4 - punktowego niejawnego.

a) napisać jak ustala się typ równania

1.

2. Pochodne zastępuje się analogiami różnicowymi.

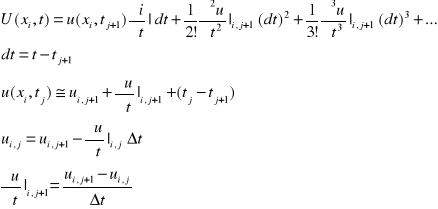
b) narysować omawiamy schemat

c) podać przykład zagadnienia, określić niewiadomą warunek obszar, warunek którym jest wyznaczana

warunek początkowy

U(x;0)=f(x) WP

U(0;t)=φ(t) LWB lewy warunek brzegowy

U(l;t)=ψ(t) PWB prawy warunek brzegowy

d) opisać jak powstaje i jakim jest wyrażona wzorem, postać różnicowa równania różniczkowego, związana z omawianym schematem, zaznaczyć w równaniu niewiadome

postać różnicowa równania:

-rU_i-1,j+1+(1+2r)U_i,j+1-rU_i+1,j+1=U_i,j aby je znaleźć trzeba utworzyć tyle równań ile niewiadomych

_____ niewiadome

e) co to znaczy, że schemat jest stabilny? Podać warunek stabilności rozważanego schematu

Warunek stabilności schematu różnicowego czteropunktowego:

aby w miarę oddalenia się błąd nie wzrastał do nieskończoności

- przy tym warunku schemat jest stabilny (błąd nie rośnie do nieskończoności)

schemat niejawny jest bezwarunkowo stabilny

Zalety schematu niejawnego: nie ma kwestii stabilności- schemat jest bezwarunkowo stabilny.

f) opisać w jakich punktach i w jakiej kolejności obliczane są wartości niewiadomej

W równaniu są trzy niewiadome, natomiast wiadoma tylko jedna dlatego mówimy, że schemat jen niejawny.

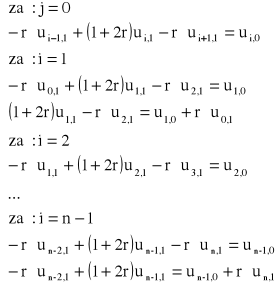
„n-1” równań przy „n-1” niewiadomych.

	U11	U21	...	Un-2,1	Un-1,1
i=1	1+2r,	-r,	0	...,	0	U11
i=2	-r,	1+2r,	0	...,	0	U21
: :						: :
i=n-1	0,	0,	...,	-r,	1+2r	Un-1,1

Taki układ równań ma zawsze jedno rozwiązanie

15. Rozwiązanie zagadnienia początkowo - brzegowego, z równaniem różniczkowym typu parabolicznego, przy użyciu schematu 4 - punktowego jawnego.

a)napisać jak ustala się typ równania,

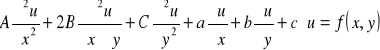
RRC-rzII-post.og.

Δ = A*C-B² u(x,y) -niewiadoma jest zawsze f.liniową;

Δ>0 - r.eliptyczne Δ<0 - r.hiperboliczne Δ= 0 - r.paraboliczne

b)narysować omawiany schemat,

c) podać przykład zagadnienia (równanie, warunek początkowy, warunki brzegowe), określić niewiadomą i obszar, w którym jest wyznaczana,

Równanie przewodnictwa cieplnego, [r.paraboliczne (A=a²,B=0,C=0)]

=> niewiadoma u(x,t)-temp. pręta w pkt. x w chwili t

Znamy wartości niewiadomej na brzegach obszaru =>warunki:

u(x,0)=f(x) WP;

u(0,t)=φ(t) LewyWB;

u(l,t)=ψ(x) PrawyWB; l-dłg.pręta

Cały układ (4równ) to zagadnienie początkowo-brzegowe(mieszane).

d) opisać jak powstaje i jakim jest wyrażona wzorem, postać różnicowa równania różniczkowego, związana z omawianym schematem. Zaznaczyć w równaniu niewiadome,

(Algorytm)

Rozwiązujemy metodą różnic skończonych.

1.Nakładamy na obszar siatkę x ^x b (rys u góry)

2.Rozwiązanie dyskretne

oznaczenie u(x_i,t_j)=u_ij ; i=0,…,n; j=0,…,k; rozw. przybliżone.

3.Postać różnicowa RR [0]

- Pochodne zastępuje się analogami różnicowymi.

4. Schemat różnicowy 4-pkt.jawny (z 1 rów. znajdujemy 1 rozw.) :

[1]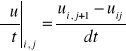

[2]

do rów. [0] podstawiamy równ.[1] i [2] i otrzymujemy

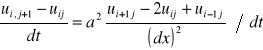
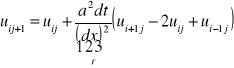
Ostateczna postać RR przy sch. jawnym.

JAWNY-górna wartość f. jest niewiadoma, 3 pozostałe są znane.

f) opisać w jakich punktach i w jakiej kolejności obliczane są wartości niewiadomej.

wyznaczanie niewiadomych z postaci różnicowej np.

dla j = 0 , i = 1

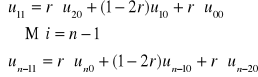
LWB: u₀₁= φ(t₁) PWB: u_n1 = ψ(t₁)

dla j = 1 , i = 1

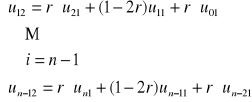
LWB: u₀₂= φ(t₂) PWB: u_n2 = ψ(t₂)

e) co to znaczy, że schemat jest stabilny? Podać warunek stabilności rozważanego schematu.

War.stabilności-aby w miarę oddalania się błąd nie wzrastał do nieskończoności. Schemat jest stabilny przy r<0,5 -błąd nie roś. do n.)

gdy
=> aby r było małe trzeba manipulować dt

a x₁ x₂ b

(x_o)

f(x)

t

t_j+1

t_j

a⁽ⁱ⁾+b⁽ⁱ⁾(x-x_i)

y

y₁

y_o

x_o x₁ x₂ x_i X x_n x

f(x)

y

x

a x₁ x₁ x_n-1 b b x₂ (x_n)

(x_o, f(x_o))

Y

x₁ X x

x*

x_o

Yy

qsqsqs

Yy

x_o x₁ x_i x_i+1 x_n-1 x_n X

Yt

y

x

x_i-1 x_i x_i+1

---