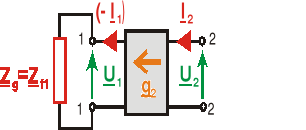
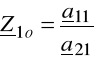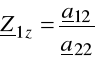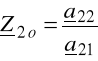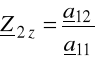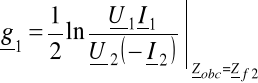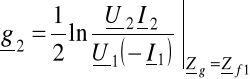6.3.3. KLASYFIKACJA CZWÓRNIKÓW

Czwórnik pasywny i aktywny

Czwórnik nazywamy pasywnym, jeżeli przy początkowej energii zgromadzonej w układzie równej zeru, całkowita energia dostarczona do niego jest nieujemna:

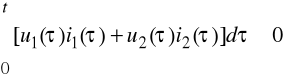
(6.30)

Niespełnienie tego warunku oznacza aktywność czwórnika.

W stanie ustalonym przy wymuszeniach harmonicznych:

• czwórnik jest PASYWNY jeśli moc czynna pobierana przez wrota czwórnika jest nieujemna dla każdej pary napięć i prądów zaciskowych

(6.31)

• czwórnik jest AKTYWNY, jeśli istnieją takie wartości napięć i prądów zaciskowych, dla których pobierana przez wrota moc czynna jest ujemna

(6.32)

Czwórnik prawidłowy i nieprawidłowy

Czwórnik klasy SLS nazywamy czwórnikiem prawidłowym, jeśli posiada wszystkie macierze charakterystyczne.

Warunkiem koniecznym i wystarczającym prawidłowości czwórnika jest aby dowolna z jego macierzy charakterystycznych była nieosobliwa, a wszystkie jej elementy były różne od zera. Macierze charakterystyczne Y , Z oraz H , G są parami macierzami odwrotnymi:

Z∙= Y^-1 ; G = H^-1 (6.33)

Czwórnik nazywamy zdegenerowanym (nieprawidłowym), jeśli posiada nie więcej niż pięć i nie mniej niż dwie macierze charakterystyczne.

Czwórnik, który posiada wyłącznie jedną macierz charakterystyczną nazywamy zerowym.

Czwórnik bilateralny, unilateralny i nielateralny

Ze względu na zdolność do przesyłania sygnałów w obu lub jednym kierunku, czwórnik nazywamy:

BILATERALNYM	- jeśli posiada obydwie macierze łańcuchowe ( A i B ) - co oznacza możliwość przesyłania sygnałów w obie strony.
UNILATERALNYM	- jeśli posiada tylko jedną macierz łańcuchową ( A lub B ): gdy istnieje tylko macierz A - to czwórnik ma zdolność przesyłania sygnałów od zacisków pierwotnych do wtórnych; gdy istnieje tylko macierz B - to czwórnik ma zdolność przesyłania sygnałów od zacisków wtórnych do pierwotnych.
NIELATERALNYM	- jeśli nie posiada żadnej macierzy łańcuchowej - co oznacza niezdolność do przesyłania sygnałów.

Czwórnik odwracalny i nieodwracalny

Czwórnik, który spełnia zasadę wzajemności nazywamy czwórnikiem ODWRACALNYM lub inaczej ENERGETYCZNIE SYMETRYCZNYM. Zgodnie z zasadą wzajemności warunki odwracalności czwórnika można wyrazić za pomocą elementów macierzy charakterystycznych:

Macierz	Y	Z	A	B	H	G
Czwórnik odwracalny	y12= y21	z12= z21	det A=1	det B=1	h12= - h21	g12= - g21

Czwórnik, który nie spełnia zasady wzajemności jest czwórnikiem nieodwracalnym.

Czwórnik symetryczny i niesymetryczny

Czwórnik, który spełnia zasadę wzajemności, a ponadto zamiana miejscami wrót wejściowych z wyjściowymi tego czwórnika nie powoduje żadnych zmian wielkości elektrycznych zaciskowych, nazywamy CZWÓRNIKIEM SYMETRYCZNYM lub inaczej IMPEDANCYJNIE SYMETRYCZNYM.

Konsekwencją symetryczności czwórnika są szczególne własności jego macierzy charakterystycznych:

Macierz	Y	Z	A	B	H	G
Czwórnik symetryczny
		y12= y21	z12= z21	det A=1	det B=1	h12= - h21	g12= - g21
		y11= y22	z11= z22	a11= a22	b11= b22	det H=1	det G=1

UWAGA: nie każdy czwórnik odwracalny jest symetryczny - warunkiem koniecznym symetryczności czwórnika jest jego odwracalność.

6.3.4. PARAMETRY ROBOCZE CZWÓRNIKA

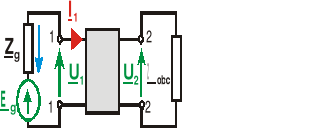
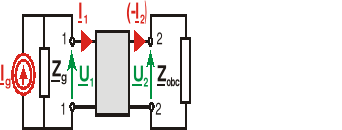
Jeżeli do jednych wrót czwórnika dołączono źródło wymuszeń, natomiast drugie wrota obciążono dwójnikiem bezźródłowym, to czwórnik taki pracuje w układzie przesyłowym i charakteryzują go parametry robocze.

Przyjmujemy założenie, że źródło wymuszeń o napięciu źródłowym E_g i impedancji wewnętrznej Z_g dołączono do wrót pierwotnych, a wrota wtórne czwórnika obciążono dwójnikiem o impedancji Z_obc

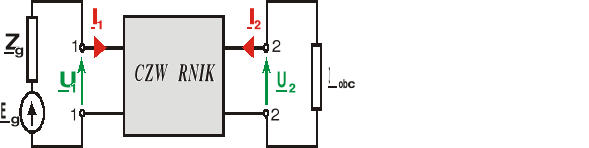
Do parametrów roboczych czwórnika klasy SLS - należy:

1. IMPEDANCYJA WEJŚCIOWA PIERWOTNA

określana jest na zaciskach pierwotnych jako stosunek napięcia do prądu pierwotnego przy obciążeniu czwórnika po stronie wtórnej dwójnikiem o impedancji Z_obc

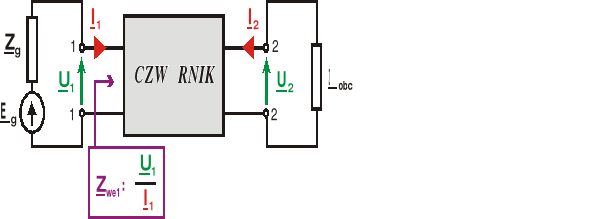
Jeśli czwórnik opisuje się równaniami impedancyjnymi to z pierwszego równania (6.20):

⇒

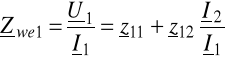
Natomiast z drugiego równania po uwzględnieniu, że

⇒

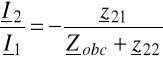
Stąd: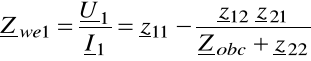
(6.34)

W granicznym przypadku gdy strona wtórna jest:

• rozwarta (Z_obc = ∞ ), impedancja ta staje się

impedancją wejściową pierwotną rozwarciową Z_1o i wynosi

(6.35)

• zwarta (Z_obc = 0 ), impedancja ta staje się

impedancją wejściową pierwotną zwarciową Z_1z i wynosi

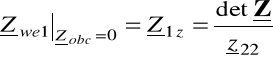
(6.36)

2. IMPEDANCYJA WEJŚCIOWA WTÓRNA

jest impedancją widzianą z zacisków wtórnych czwórnika (przy E_g = 0) i wyraża się stosunkiem napięcia do prądu wtórnego

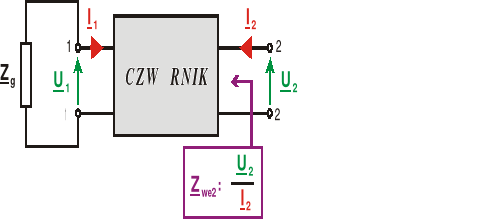
Z drugiego równania (6.20) otrzymujemy

⇒

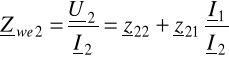
Natomiast z drugiego równania po uwzględnieniu, że

⇒

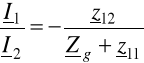
Stąd: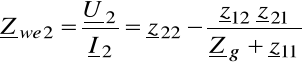
(6.37)

W granicznych przypadkach Z_we2 staje się:

• impedancją wejściową wtórną rozwarciową Z_2o

(6.38)

• impedancją wejściową wtórną zwarciową Z_2z

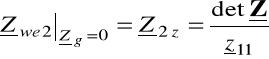
(6.39)

UWAGA:

Tak określone impedancje zwarciowe i rozwarciowe, pierwotne i wtórne związane są zależnością:

3. WZMOCNIENIE NAPIĘCIOWE (TRANSMITANCJA NAPIĘCIOWA)

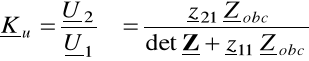
(6.40)

Gdy uwzględni się fakt zasilania z rzeczywistego źródła energii, mówimy o skutecznym (efektywnym) wzmocnieniu napięciowym:

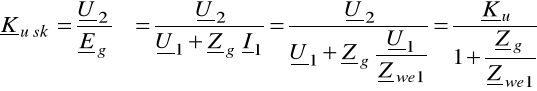
(6.41)

4. WZMOCNIENIE PRĄDOWE (TRANSMITANCJA PRĄDOWA)

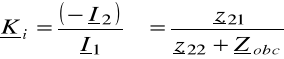
(6.42)

Gdy uwzględni się fakt zasilania z rzeczywistego źródła energii, mówimy o skutecznym (efektywnym) wzmocnieniu prądowym:

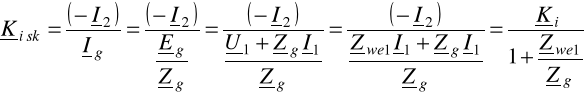
(6.43)

UWAGA: Wszystkie określone powyżej transmitancje (wzmocnienia) mogą być również wyrażone w mierze logarytmicznej:

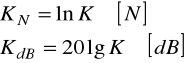
6.3.5. PARAMETRY FALOWE CZWÓRNIKA

Parametry falowe czwórnika określane są dla szczególnych warunków pracy czwórnika a mianowicie przy tzw. dopasowaniu falowym.

IMPEDANCJE FALOWE

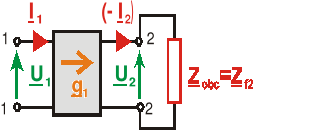
Rozważmy czwórnik pracujący w układzie przesyłowym i załóżmy, że jest on opisany parametrami łańcuchowymi - wówczas:

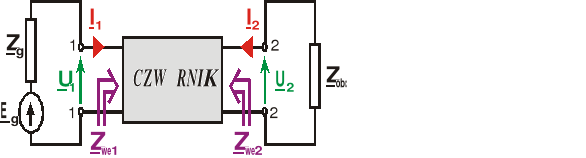
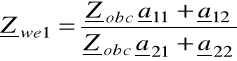
(6.44)

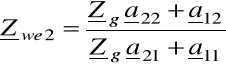
(6.45)

Żądając aby
(6.46)

otrzymuje się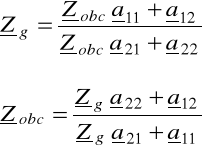
(6.47)

Impedancje Z_g i Z_obc, będące rozwiązaniami układu równań (6.47) nazywają się impedancjami falowymi (charakterystycznymi) czwórnika i wyrażają się wzorami:

impedancja falowa pierwotna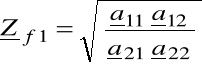
(6.48)

impedancja falowa wtórna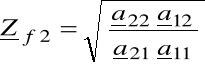
(6.49)

Jest to zatem para impedancji o takiej właściwości, że

• Jeśli Z_g=Z_f1, to mówimy że czwórnik jest dopasowany falowo na wejściu (wówczas impedancja wejściowa wtórna jest równa jego impedancji falowej wtórnej).

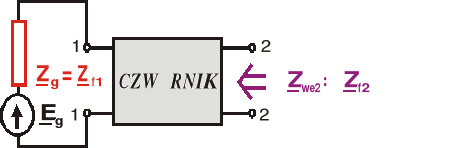
• Jeżeli natomiast Z_obc=Z_f2, to mówimy, że czwórnik jest dopasowany falowo na wyjściu (wówczas impedancja wejściowa pierwotna jest równa jego impedancji falowej pierwotnej)

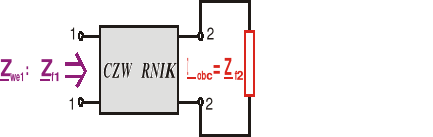
Jeśli czwórnik jest dopasowany na wejściu i na wyjściu to mówimy, że jest obustronnie dopasowany falowo (w stanie dopasowania falowego),

UWAGA: Impedancje falowe są parametrami własnymi czwórnika, tzn. zależą tylko od właściwości samego czwórnika!

Impedancje falowe można uzależnić od impedancji wejściowych stanu jałowego i stanu zwarcia.

Ponieważ impedancja wejściowa pierwotna:

rozwarciowa (6.50)

zwarciowa (6.51)

natomiast impedancja wejściowa wtórna:

rozwarciowa (6.52)

zwarciowa (6.53)

Zatem: impedancja falowa pierwotna
(6.54)

impedancja falowa wtórna
(6.55)

IMPEDANCJĘ FALOWĄ ŚREDNIĄ CZWÓRNIKA określamy jako średnią geometryczną impedancji falowej pierwotnej i wtórnej

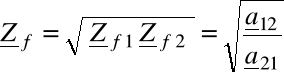
(6.56)

Jeśli czwórnik jest symetryczny (a₁₁=a₂₂) to posiada tylko jedną impedancję falową

(6.57)

Dla czwórnika niesymetrycznego możemy również posługiwać się pojęciem przekładni impedancyjnej czwórnika określonej następująco:

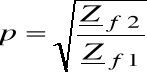
(6.58)

Można wykazać, że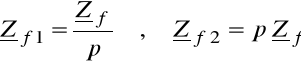
(6.59)

TAMOWNOŚĆ FALOWA (współczynnik przenoszenia falowego)

Drugim istotnym parametrem falowym czwórnika jest tamowność falowa „g”. Określa się ją dla czwórnika DOPASOWANEGO FALOWO NA

• WYJŚCIU jako tamowność falową pierwotną

(6.60)

• WEJŚCIU jako tamowność falową wtórną

(6.61)

Definiuje się także tamowność falową średnią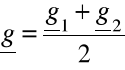
(6.62)

Współczynniki g₁ i g₂ można wyrazić za pomocą macierzy łańcuchowej czwórnika:


(6.63)


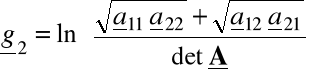
(6.64)

Z równań (6.63 i 64) wynika, że dla czwórników odwracalnych (det A=1) oba współczynniki przenoszenia są sobie równe


(6.65)

Warunki transmisji sygnałów przez czwórnik odwracalny są dla obu kierunków transmisji identyczne.

Przepływ energii odbywa się w sposób symetryczny.

====================================

Gdy czwórnik dopasowany jest falowo na wyjściu:













====================================

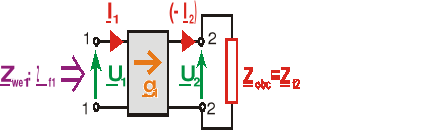
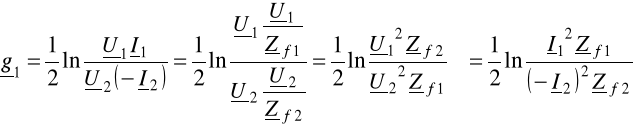
W przypadku czwórnika symetrycznego [pamiętając o (6.57)]


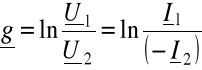
(6.66)


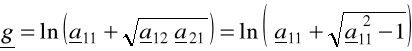
(6.67)

Ogólnie współczynnik przenoszenia falowego jest liczbą zespoloną o postaci




a + j b





====================================

Zespolone wartości skuteczne napięć zaciskowych:


,


====================================

Zgodnie z (6.66)


















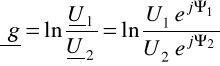
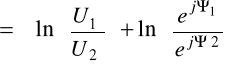
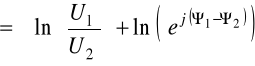
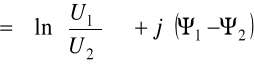
Przekształcając (6.66)




















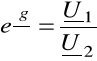
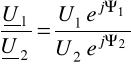
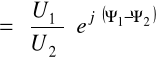
Ogólnie współczynnik przenoszenia falowego jest liczbą zespoloną o postaci




a + j b





====================================

















=







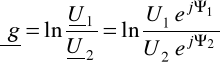
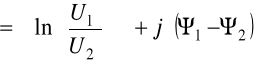
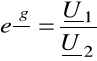
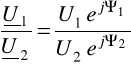
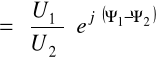
Macierz łańcuchowa w postaci hiperbolicznej







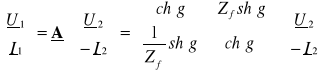
PRZYKŁAD 2: Dla czwórnika w stanie dopasowania falowego o znanej macierzy łańcuchowej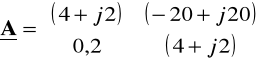


i znanym napięciu wej.


wyznaczyć: a) rozwarciową i zwarciową impedancję wejściową wtórną;

b) parametry dwójnika obciążenia;

c) napięcie wyjściowe.

Ad. a) rozwarciową impedancję wejściową wtórna (6.52)




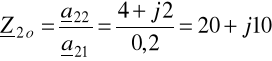
zwarciową impedancję wejściową wtórna (6.53)




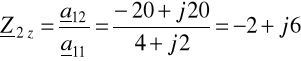
Ad. b) Z macierzy A wynika, że czwórnik jest symetryczny, czyli (6.57)






Zatem: R X_L

Znając pulsację i reaktancję indukcyjną,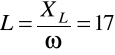
[mH]

Ad. c) Tamowność falowa (6.67)







Czyli:


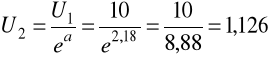
[v],





- 30 -

- 29 -

- 30a

-

- 31 -

współczynnik

tłumienia falowego

(tłumienność)

współczynnik

przesunięcia falowego

(przesuwność)

współczynnik

tłumienia falowego

(tłumienność)

współczynnik

przesunięcia falowego

(przesuwność)

---