Schemat układu pomiarowego:
99-11-16
Laboratorium fizyki II
Ćwiczenie nr: 12
Temat: Wyznaczenie parametrów mikroskopowych półprzewodników w oparciu o zjawisko Halla.
Marcin Sęk gr.2.3 zespół 2
Celem ćwiczenia było wykonanie pomiarów oraz obliczeń związanych z tematem a mianowicie - wartość przewodności, ruchliwości nośników prądu itp.
Ćwiczenie to zaczęliśmy od zapoznania się z układem pomiarowym (zasilacz stabilizowany, amperomierz, opornik, cewka itp.), z którym mieliśmy do czynienia w laboratorium oraz z przypomnieniem podstawowych pojęć związanych z tematem.
Zasilacz - urządzenie dostarczające energię elektryczną do układów elektrycznych; sieciowy, bateryjny; główna część transformatora, prostownika, stabilizatora.
Opornik - element bierny obwodu elektrycznego, którego główną właściwością fizyczną jest rezystancja.
Woltomierz - miernik elektryczny, wyskalowany w woltach, do mierzenia napięcia elektrycznego, siły elektromotorycznej, potencjału elektrycznego itp.
Amperomierz - miernik elektryczny wyskalowany w amperach; do mierzenia prądu elektrycznego, włączany szeregowo w badany obwód prądu elektrycznego.
Cewka - przewód elektryczny izolowany, zwinięty w szereg zwojów, najczęściej na kadłubie z materiału elektroizolacyjnego, wg linii śrubowej, w taki sposób, że wszystkie zwoje można uważać w przybliżeniu za prostopadłe do osi cewki; cewka służy do wytwarzania pola magnetycznego (cewka wzbudzająca) lub do zwiększania indukcyjności obwodu (cewka indukcyjna).
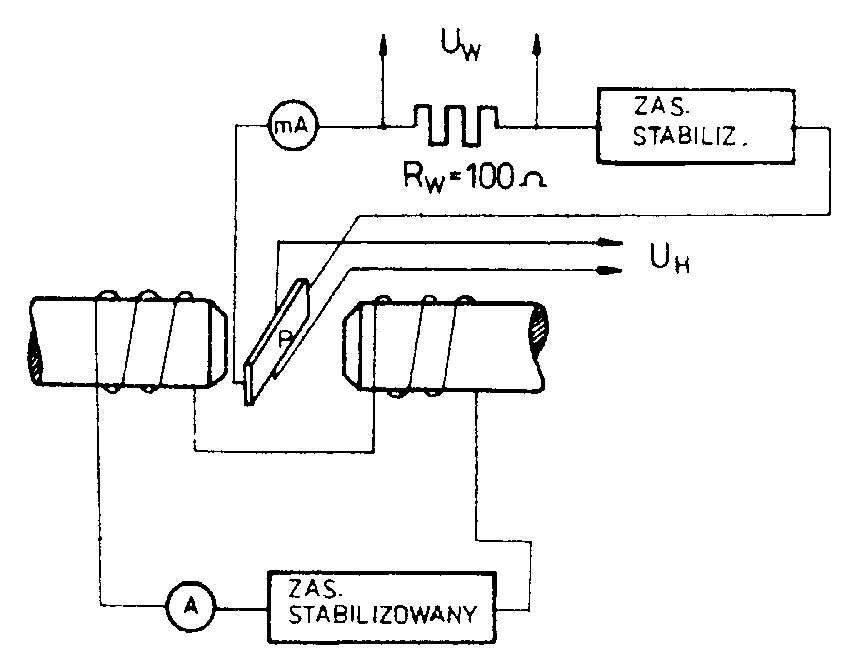
Schemat układu pomiarowego:
Gęstość prądu j - całkowity ładunek, jaki przepływa przez przekrój przewodnika w jednostce czasu. W przypadku występowania tylko jednego rodzaju nośnika jest ona równa iloczynowi ładunku pojedynczego nośnika i liczby nośników w jednostce objętości, czyli ich koncentracji oraz prędkości.
Mikroskopowa postać prawa Ohma - jest po prostu inaczej zapisanym prawem opisującym proporcjonalność prądu do przyłożonego napięcia.
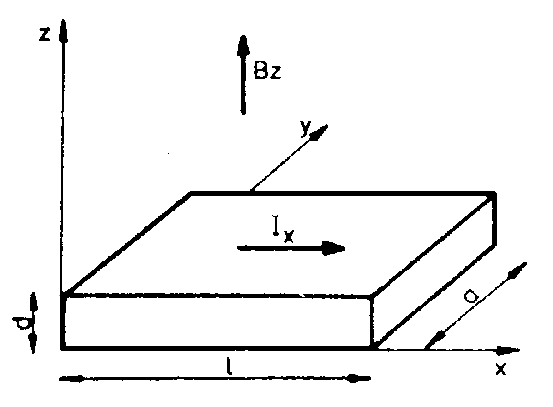
Wielkości takie jak znak nośników prądu, ich koncentracja i ruchliwość, nazywane są mikroskopowymi parametrami półprzewodnika. Jedną z metod ich wyznaczania jest pomiar oparty na zjawisku Halla.
Zjawisko Halla.
Jeśli próbkę wykonaną z metalu lub półprzewodnika, przez którą płynie prąd o natężeniu I (wzdłuż osi x) wywołany zewnętrznym polem elektrycznym E umieścimy w polu magnetycznym o indukcji B, skierowanym prostopadle do kierunku płynącego prądu (wzdłuż osi z), to pomiędzy ściankami próbki w kierunku y zaobserwujemy różnicę potencjałów zwaną napięciem Halla. Wielkość napięcia Halla jest wprost proporcjonalna do natężenia prądu i indukcji magnetycznej a odwrotnie proporcjonalna do grubości próbki d.
Wykonanie ćwiczenia i otrzymane wyniki.
Zaczęliśmy od zestawienia układu pomiarowego według wyżej przedstawionego schematu.
Następnie ustawiliśmy prąd płynący przez próbkę na wartość 1,5mA (zasilacz pracuje jako stabilizator prądu, a nie napięcia) i zmierzyliśmy wartość poprzecznego napięcia w próbce przy wyłączonym polu magnetycznym - otrzymaliśmy następującą wartość napięcia asymetrii: 
.
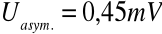
Potem przystąpiliśmy do wykonania pomiarów napięcia Halla w zależności od wartości prądu płynącego przez cewkę. Dokonywaliśmy pomiarów dla natężenia od 0,5A - 6A (amperów), co 0,5A. Dzięki skorzystaniu z wykresu zależności wartości natężenia prądu płynącego przez cewkę w funkcji indukcji magnetycznej mogliśmy podać również wartość indukcji magnetycznej B [T] (odczytując wartość B dla danego I - przy odczytywaniu braliśmy pod uwagę wartość napięcia asymetrii).
Wykres zależności natężenia I [A] w funkcji indukcji magnetycznej B [T].
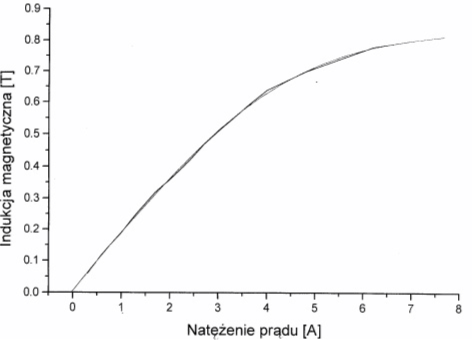
Następnie powtórzyliśmy wszystkie pomiary dla prądu 3mA - metody pomiarowe przebiegały tak samo jak dla prądu 1,5mA.
Wszystkie otrzymane wyniki dla obu prądów umieściliśmy w tabelce - otrzymując:
I = 1,5 [mA] |
I = 3 [mA] |
||||||
Uzasila. [V] |
Iprąd.ce. [A] |
B [T] |
UH [V] |
Uzasila. [V] |
Iprąd.ce. [A] |
B [T] |
UH [V] |
2 |
0,5 |
0,093 |
-3,14 |
2 |
0,65 |
0,123 |
-8,08 |
4 |
1,25 |
0,234 |
-8,31 |
3 |
1 |
0,185 |
-12,65 |
5 |
1,6 |
0,310 |
-10,43 |
4 |
1,4 |
0,265 |
-17,41 |
6 |
1,9 |
0,350 |
-12,51 |
6 |
2 |
0,362 |
-25,58 |
8 |
2,55 |
0,445 |
-16,54 |
7 |
2,35 |
0,412 |
-29,72 |
9 |
2,9 |
0,490 |
-18,48 |
9 |
3 |
0,511 |
-36,61 |
10 |
3,5 |
0,575 |
-21,09 |
10 |
3,5 |
0,575 |
-41,05 |
11 |
3,9 |
0,634 |
-22,50 |
11 |
3,9 |
0,634 |
-43,34 |
13 |
4,5 |
0,675 |
-24,44 |
13 |
4,5 |
0,675 |
-46,93 |
14 |
5 |
0,712 |
-25,45 |
14 |
5 |
0,712 |
-48,83 |
16 |
5,7 |
0,755 |
-26,81 |
16 |
5,6 |
0,745 |
-51,42 |
17 |
6 |
0,785 |
-27,47 |
17 |
6 |
0,785 |
-52,54 |
Kolejnym etapem ćwiczenia było wyznaczenie oporu próbki mierząc spadek napięcia na próbce między elektrodami prądowymi Ux i spadek napięcia na oporze wzorcowym Uw. Dzięki temu, że oba opory są połączone szeregowo, opór próbki obliczyliśmy korzystając z proporcji: 
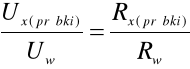
; po przekształceniu otrzymujemy: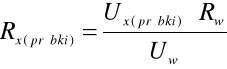 
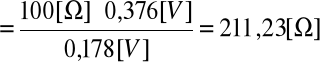
. Następnie obliczyliśmy błąd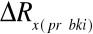 
korzystając z metody różniczki zupełnej: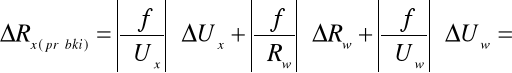 
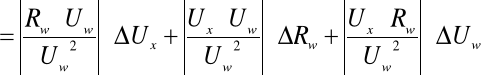
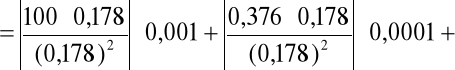
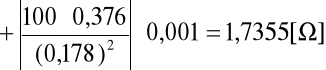
czyli: Rx(próbki) = 211,2 ± 1,8 [Ω].
Po wyznaczeniu oporu próbki obliczyliśmy przewodność właściwą próbki ze wzoru: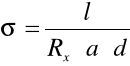
(gdzie: l = 0,0078 m; d = 0,3 10 -6 m; a = 0,004 m) podstawiając dane do wzoru otrzymujemy: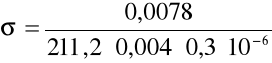 
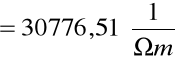
. Po wyliczeniu tej wartości przystąpiliśmy do obliczenia jej błędu stosując metodę różniczki zupełnej: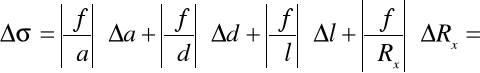 
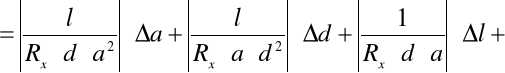
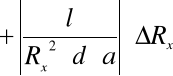
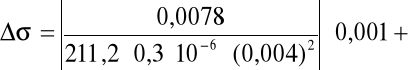
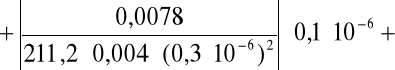
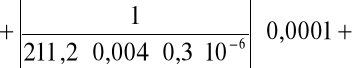
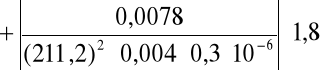
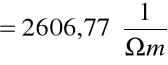
a więc: Δσ = 30776,5 ± 2606,8 [1/Ωm].
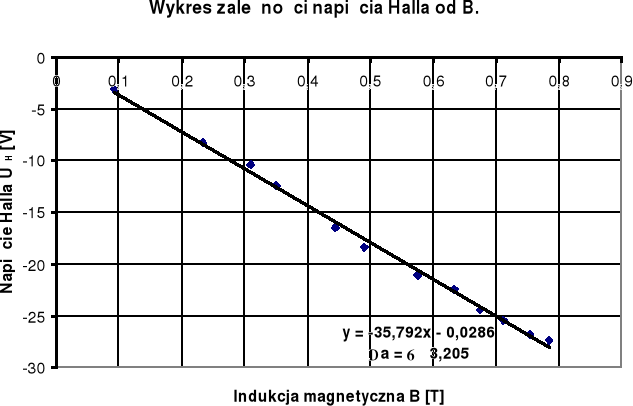
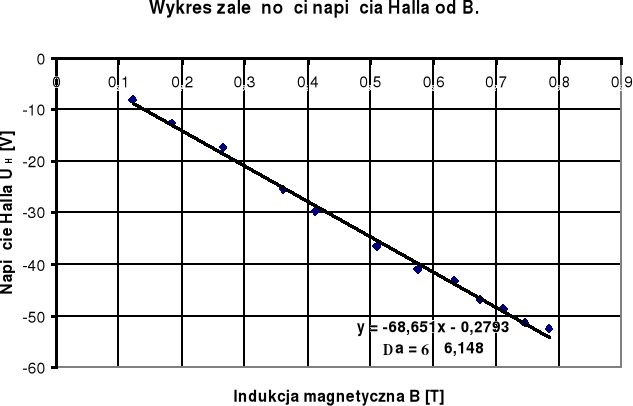
Następnie wykonaliśmy wykres zależności napięcia Halla UH od B i obliczyliśmy stałą Halla RH wykorzystując metodę najmniejszych kwadratów (skorzystaliśmy z komputera, który obliczył wartość stałej i jej błąd) dla obu prądów sterujących a mianowicie:
dla prądu sterującego I = 1,5mA = 1,5 10 -3V
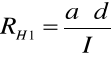
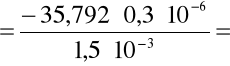
- 0,007158 = - 7,158 10 -3. Następnie korzystając z metody różniczki zupełnej obliczyłem błąd tej wartości:
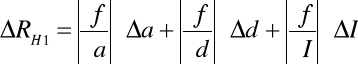
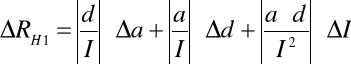
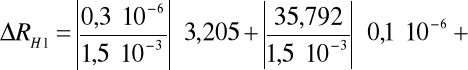
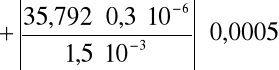
dla prądu sterującego I = 3mA = 3 10 -3V
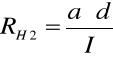
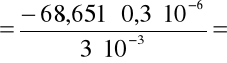
- 0,006865 = - 6,865 10 -3. Następnie korzystając z metody różniczki zupełnej obliczyłem błąd tej wartości:
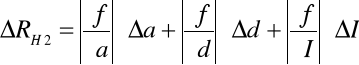
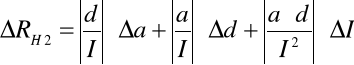
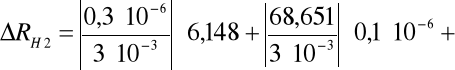
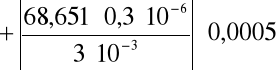
Po obliczeniach oceniliśmy wartość błędu RH i porównaliśmy obie otrzymane wartości czy są takie same w granicach tego błędu a więc:
dla prądu sterującego I = 1,5mA:
RH1 = - (7,16 ± 0,60) 10 -3[m 3/A s]
dla prądu sterującego I = 3mA:
RH2 = - (6,87 ± 0,57) 10 -3[m 3/A s].
Obie otrzymane wartości zgadzają się w granicach błędu. Następnie uśredniliśmy RH1 i RH2 i ich błędy otrzymując RH i jego błąd: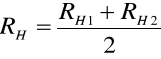 
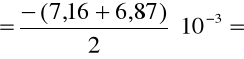
= - 7,015 10 -3,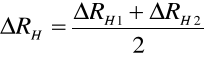 
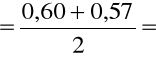
= 0,585 a więc: RH = - (7,02 ± 0,59) 10 -3[m 3/C].
Stała Halla zależy od rodzaju materiału płytki, jego częstości, temperatury; znak zależy od typu przewodnictwa: ujemny dla materiałów o przewodnictwie elektronowym, dodatni dla materiałów o przewodnictwie, dziurowym.
W kolejny etapie korzystając z wyznaczonych wartości przewodności i stałej Halla obliczyliśmy koncentrację i ruchliwość nośników prądu korzystając z następujących wzorów:
koncentracja - 
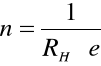
(gdzie: e = 1,60217733 10 -19 C ładunek elementarny) podstawiając odpowiednie dane otrzymujemy: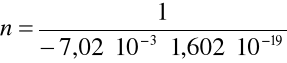 
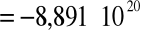
ruchliwość - 
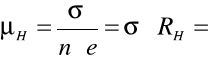
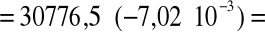
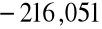
Następnie określiliśmy błąd wyznaczenia koncentracji n i ruchliwości korzystając z metody różniczki zupełnej a mianowicie:
błąd:
=
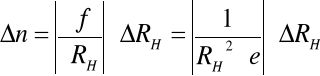
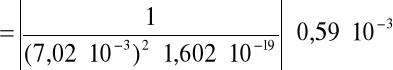
czyli: n = - (8,89 ± 0,75) 10 20[ 1/m 3].
błąd:
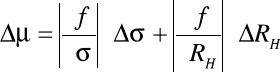
36,457
czyli: μH = - 216,01 ± 36,46 [m 2/Ω C ].
Wnioski.
Powyższe pomiary i obliczenia pozwoliły nam na wyznaczenie poszukiwanych wartości (stałej Halla, koncentracji i ruchliwości nośników, przewodności). Wartości, które otrzymaliśmy z obliczeń zgadzają się w granicach błędu z wartościami tablicowymi - teoretycznymi, co może świadczyć o poprawnym wykonaniu ćwiczenia. W ćwiczeniu tym mogliśmy zaobserwować zjawisko Halla; poznaliśmy również jego praktyczne zastosowanie i zasadę działania układu pomiarowego, z jakim mieliśmy do czynienia w laboratorium.
1