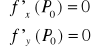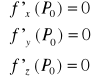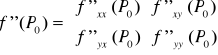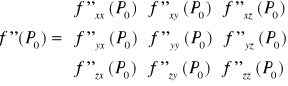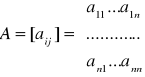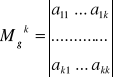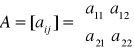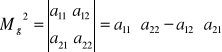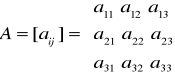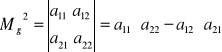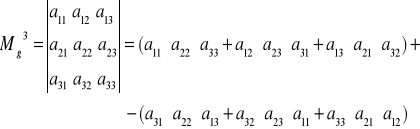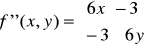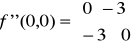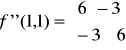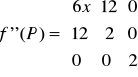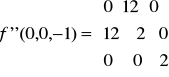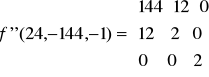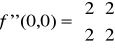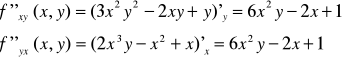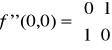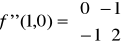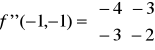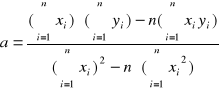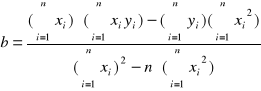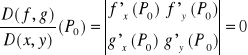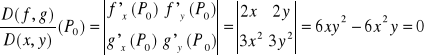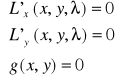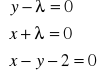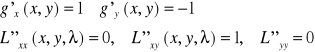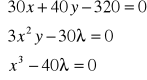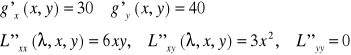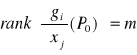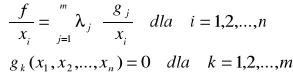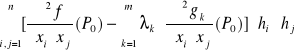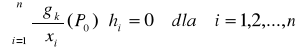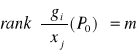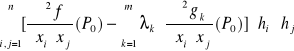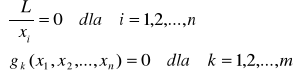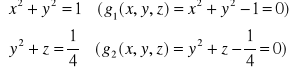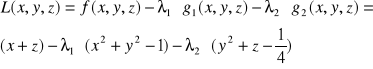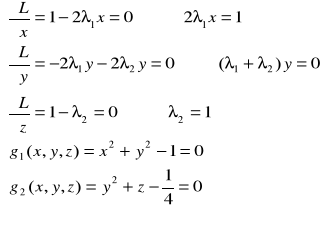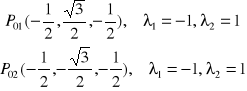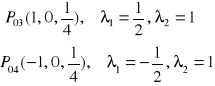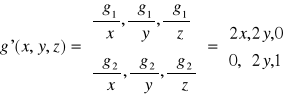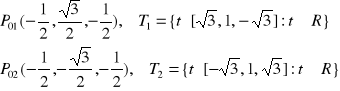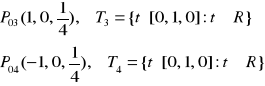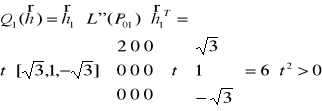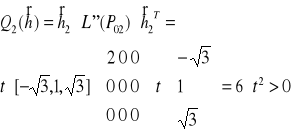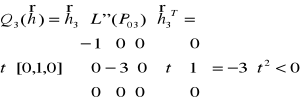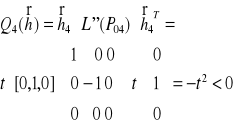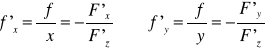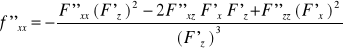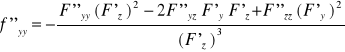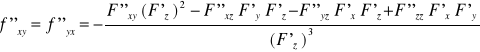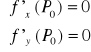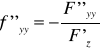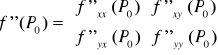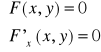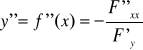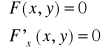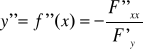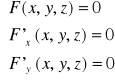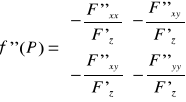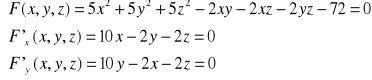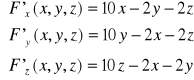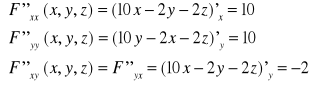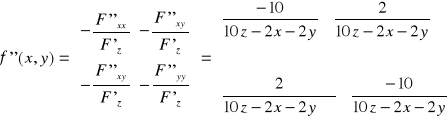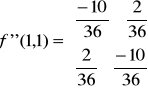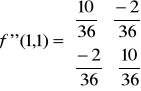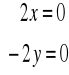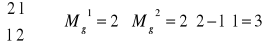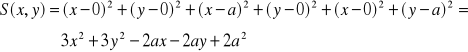AM2:WYKŁAD-4

Ekstrema lokalne funkcji wielu zmiennych Ekstrema lokalne warunkowe funkcji wielu zmiennych Ekstrema lokalne funkcji uwikłanej dwóch zmiennych Ekstrema globalne (absolutne) funkcji wielu zmiennych Optymalizacja funkcji 2 i 3 zmiennych

Na początku zdefiniujemy pojęcie ekstremum lokalnego

(minimum lub maksimum) funkcji o dowolnej ilości zmiennych.

Funkcja f(P) ma w punkcie P0 minimum lokalne Jeżeli to mówimy o minimum lokalnym właściwym

Funkcja f(P) ma w punkcie P0 maksimum lokalne Jeżeli to mówimy o maksimum lokalnym właściwym

Jak widać definicje te są niezależne od ilości argumentów danej funkcji

pod warunkiem że mamy określone sąsiedztwo danego punktu ( metrykę ) .

Jeżeli funkcja f(P) ma ekstremum lokalne w punkcie P0 istnieją wszystkie pochodne cząstkowe w punkcie P0 to wówczas

Zatem ekstremów lokalnych należy poszukiwać:

• w punktach osobliwych (w których pochodna nie istnieje)

• w punktach krytycznych(stacjonarnych) dla których pochodna istnieje i jest =0

Spróbujmy syntetycznie ująć warunki konieczne i dostateczne istnienia ekstremów lokalnych dla funkcji 1, 2 i 3 zmiennych.

W tabeli poniżej przedstawiono zestawienie warunków koniecznych i dostatecznych istnienia ekstremów lokalnych dla funkcji:

• 1 zmiennej (pochodne w punkcie są liczbami)

• 2 zmiennych (pochodne w punkcie są macierzami 1x2 i 2x2)

• 3 zmiennych (pochodne w punkcie są macierzami 1x3 i 3x3)

Warunek konieczny ekstremum lokalnego
y = f(x)	z = f(x,y)	t = f(x,y,z)
jedno równanie na punkty krytyczne	układ 2 równań na punkty krytyczne	układ 3 równań na punkty krytyczne
Warunek dostateczny ekstremum lokalnego
y = f(x)	z = f(x,y)	t = f(x,y,z)
minimum lokalne maksimum lokalne	dodatnio określona minimum lokalne ujemnie określona maksimum lokalne	dodatnio określona minimum lokalne ujemnie określona maksimum lokalne

Widać że dla funkcji 2 i 3 zmiennych, których pochodne reprezentowane są przez macierze, o istnieniu ekstremum przesądza dodatnia lub ujemna określoność macierzy symetrycznej.

Ale co oznacza ten termin dla macierzy o wymiarach 2x2 oraz 3x3 ?

Określimy teraz jak można wyznaczać dodatnią lub ujemną określoność macierzy symetrycznej.

Dla macierzy kwadratowej określamy minor główny stopnia k jako wyznacznik stopnia k zbudowany na bazie głównej przekątnej macierzy Dodatnią lub ujemną określoność macierzy kwadratowej symetrycznej możemy określić za pomocą minorów głównych. a) to macierz jest określona dodatnio b) to macierz jest określona ujemnie c) to macierz jest półokreślona dodatnio d) to macierz jest półokreślona ujemnie e) nie zachodzi żaden z powyższych to macierz jest nieokreślona Jeżeli macierz drugiej pochodnej jest półokreślona(dodatnio lub ujemnie) to kryterium nie rozstrzyga istnienia ekstremum lokalnego - trzeba to zrobić z definicji ekstremum lokalnego. Jeżeli macierz drugiej pochodnej jest niekreślona to w danym punkcie nie ma ekstremum lokalnego (jest to tzw. punkt siodłowy). W konkretnych przykładach ograniczymy się tylko do przypadku macierzy o wymiarach 2x2 lub 3x3.

Macierz 2x2 a) to macierz dodatnio określona b) to macierz ujemnie określona

Macierz 3x3 Wykorzystaliśmy tutaj wzór Sarrusa obliczania wyznacznika 3x3. a) to macierz dodatnio określona b) to macierz ujemnie określona

Przykład-1: ekstrema funkcji 2 zmiennych Zbadajmy istnienie ekstremów funkcji Liczymy pochodne cząstkowe I rzędu i przyrównujemy do zera: Dostajemy dwa punkty krytyczne P0 (0,0) oraz P1 (1,1). Liczymy teraz pochodne czastkowe II rzędu: zatem macierz II pochodnej w punkcie P(x,y) ma ogólną postać: Określamy teraz macierz dla punktu krytycznego P0 (0,0): Liczymy minory A zatem macierz jest nieokreślona czyli brak ekstremum w punkcie P0 (0,0). Określamy teraz macierz dla punktu krytycznego P1 (1,1): Liczymy minory a zatem macierz jest określona dodatnio czyli dostajemy minimum lokalne w punkcie P1 (1,1) a wartość minimalna .

Przykład-2: ekstrema funkcjji 3 zmiennych Zbadajmy istnienie ekstremów funkcji Liczymy pochodne cząstkowe I rzędu i przyrównujemy do zera: Dostajemy dwa punkty krytyczne P0 (0,0,-1) oraz P1 (24,-144,-1). Liczymy teraz pochodne cząstkowe II rzędu: zatem macierz II pochodnej w punkcie P(x,y) ma ogólną postać: Określamy teraz macierz dla punktu krytycznego P0 (0,0,-1): Liczymy minory Zatem macierz jest nieokreślona czyli brak ekstremum w punkcie P0 (0,0,-1). Określamy teraz macierz dla punktu krytycznego P1 (24,-144,-1). Liczymy minory a zatem macierz jest określona dodatnio czyli dostajemy minimum lokalne w punkcie P1 (24,-144,-1).

Rozważymy teraz przypadek kiedy macierz drugiej pochodnej jest półokreślona czyli nasze kryterium nie rozstrzyga istnienia ekstremum lokalnego - pozostaje nam tylko skorzystanie wprost z definicji ekstremum lokalnego

i sprawdzenie czy różnica wartości funkcji f(P)-f(P₀) jest nieujemna albo niedodatnia w pewnym sąsiedztwie punktu P₀.

Przykład Rozważmy funkcję Znajdujemy punkty krytyczne w których pochodne cząstkowe sa równe zeru. skąd otrzymujemy jedyny punkt stacjonarny P0 (0,0). Znajdujemy elementy macierzy II pochodnej i tworzymy macierz drugiej pochodnej w punkcie krytycznym (0,0) Liczymy minory główne: a zatem macierz ta jest półokreślona(dodatnio) - musimy zatem skorzystać wprost z definicji ekstremum lokalnego. Zauważamy że wzór naszej funkcji można przedstawic w postaci: oraz że Łatwo teraz zauważyć że w każdym sąsiedztwie (0,0): A zatem w punkcie (0,0) funkcja ma minimum lokalne właściwe.

Rozważmy jeszcze przypadek kiedy macierze drugiej pochodnej są nieokreślone w każdym punkcie - funkcja nie ma ekstremum lokalnego w żadnym punkcie krytycznym.

Przykład Rozważmy funkcję Znajdujemy punkty krytyczne w których pochodne cząstkowe sa równe zeru. skąd otrzymujemy trzy punkty krytyczne P01 (0,0), P02 (1,0), P03 (-1,-1). Znajdujemy elementy macierzy drugiej pochodnej: Tworzymy macierz drugiej pochodnej w punkcie krytycznym P01 (0,0). Liczymy minory główne: a zatem macierz ta jest nieokreślona - nie ma ekstremum lokalnego. Tworzymy macierz drugiej pochodnej w punkcie krytycznym P02 (1,0). Liczymy minory główne: a zatem macierz ta jest nieokreślona - nie ma ekstremum lokalnego. Tworzymy macierz drugiej pochodnej w punkcie krytycznym P03 (-1,-1). Liczymy minory główne: a zatem macierz ta jest nieokreślona - nie ma ekstremum lokalnego. Podsumowując widzimy że funkcja nie ma ekstremum lokalnego w żadnym punkcie krytycznym.

Jeszcze jednym przykładem zastosowania ekstremów funkcji wielu zmiennych jest metoda najmniejszych kwadratów stosowana w ekstrapolacji wyników pomiarów wielkości fizycznej y zależnej w od wielkości fizycznej x za pomocą funkcji z dwoma parametrami y=f(x,a,b) (np. funkcji liniowej y = ax + b).

Jeżeli dysponujemy wynikami n pomiarów wielkości x oraz y tzn. punktami:

To szukamy teraz funkcji G(a,b) zależnej od dwóch parametrów która najlepiej przybliża wyniki pomiarów tzn. szukamy minimum funkcji

Ponieważ argumentami tej funkcji są parametry a i b to wszystkie różniczkowania w analizie ekstremów funkcji G(a,b) przeprowadzamy po tych parametrach.

Przykład: Przyjmijmy że zależność między wspomnianymi wielkościami jest liniowa tzn. f(x,a,b) = ax + b Wówczas funkcja G(a,b) którą będziemy minimalizować ma postać: Obliczamy pochodne cząstkowe i przyrównujemy do zera: Dostajemy zatem układ równań liniowych na a i b: Po rozwiązaniu tego układu mamy wzory na a i b: Liczymy elementy drugiej pochodnej i minory macierzy drugiej pochodnej a zatem macierz dodatnio określona czyli minimum lokalne. Konkludując prosta y=ax+b o wyliczonych wyżej parametrach a i b najlepiej przybliża wyniki pomiarów .

Omówimy teraz przypadek ekstremum warunkowego dla funkcji 2 zmiennych który ma charakter ekstremum lokalnego przy zadanym dodatkowym warunku.

Niech f(x,y) i g(x,y) będą określone i ciągłe w obszarze D.

Funkcja z = f(x,y) osiaga w punkcie P0(x0,y0)єD minimum warunkowe przy warunku g(x,y) = 0 jeżeli:

Funkcja z = f(x,y) osiaga w punkcie P0(x0,y0)єD maksimum warunkowe przy warunku g(x,y) = 0 jeżeli:

Jeżeli funkcje f(x,y) oraz g(x,y) sa klasy C^1(D) to warunkiem koniecznym istnienia w punkcie P0(x0,y0)єD ekstremum warunkowego funkcji f(x,y) przy warunku g(x,y) = 0 jest spełnienie równości: gdzie D(f,g)/D(x,y) jest wyznacznikiem funkcyjnym Jacobiego (jakobianem). Wniosek: Wszystkie możliwe punkty krytyczne znajdziemy z układu równań

Często stosujemy ogólniejszą metodę Lagrange'a czynnika nieoznaczonego λ. Polega ona na: -wprowadzeniu pomocniczej funkcji Lagrange'a , -wypisaniu warunku koniecznego ekstremum funkcji 2 zmiennych -wyrugowaniu z układu równań czynnika nieoznaczonego λ.

Przykład-1 Wyznaczmy ekstrema funkcji przy warunku Szukamy rozwiązań układu równań: Obliczamy elementy jakobianu: i rozwiązujemy układ równań: Ma on trzy rozwiązania: Sprawdzamy czy w tych punktach równanie g(x,y) = 0 wyznacza funkcję uwikłaną y=y(x). Okazuje się że w punktach są spełnione założenia o istnieniu funkcji uwikłanej y=y(x) a w punkcie nie są spełnione. Uwzględniając że y=y(x) liczymy pochodne funkcji z = z(x) = f(x,y(x)) Żeby okreslić ekstrema funkcji z(x) musimy sprawdzić warunek konieczny ( ) i dostateczny ekstremów lokalnych. w punktach . Jak widać z powyższych wzorów potrzebna nam jest znajomość pierwszej i drugiej pochodnej funkcji y(x) tzn. y' oraz y'' w tych punktach. Pochodne te obliczamy z równania uwikłanego różniczkując je kolejno dwa razy i wyliczając y'(x) oraz y''(x). Pierwsze rózniczkowanie daje: Pierwsza pochodna w punkcie Pierwsza pochodna w punkcie Drugie różniczkowanie daje: Druga pochodna w punkcie Druga pochodna w punkcie Łatwo już teraz zauważyć że warunek konieczny dla funkcji z(x): w punkcie w punkcie jest spełniony w obu punktach. Warunek dostateczny dla ekstremów funkcji z(x): w punkcie a więc maksimum lokalne = 8 w punkcie a więc minimum lokalne = Zaznaczyć należy że są to ekstrema lokalne warunkowe.

Przykład-2 Wyznaczmy ekstrema funkcji przy warunku metodą Lagrange'a. Tworzymy funkcję pomocniczą: Liczymy jej pochodne cząstkowe i przyrównujemy do zera. Z równań tych eliminujemy czynnik nieoznaczony i otrzymujemy równanie: dołączamy do niego równanie warunku: i rozwiązujemy powyższy układ równań otrzymując 4 rozwiązania: We wszystkich tych punktach równanie określa funkcję uwikłaną y=y(x). Podobnie jak w poprzednim przykładzie można pokazać że dla funkcji z=z(x)=xy(x) : w punkcie mamy maksimum lokalne warunkowe w punkcie mamy minimum lokalne warunkowe w punkcie mamy minimum lokalne warunkowe w punkcie mamy maksimum lokalne warunkowe

Po tych przykładach pojawia się pytanie czy dla określenia warunku dostatecznego ekstremum warunkowego koniecznie musimy korzystać bezpośrednio z teorii funkcji uwikłanej - czy nie ma kryterium analogicznego do kryterium ekstremum lokalnego ? Odpowiedź jest pozytywna.

Niech funkcje f(x,y) oraz g(x,y) sa klasy C^1(D). W punkcie P0(x0,y0)єD szukamy ekstremum warunkowego funkcji f(x,y) przy warunku g(x,y) = 0. Wprowadzamy funkcję 1.Rozwiązujemy układ równań: 2. Znajdujemy rozwiązania - trójki liczb postaci 3. Tworzymy funkcję 3 zmiennych 4. Obliczamy dla każdej trójki wartość : Jeżeli Jeżeli

Przykład-1 Wyznaczymy ekstrema funkcji przy warunku opisaną metodą. Tworzymy funkcję pomocniczą i jej pochodne: Tworzymy układ równań: Rozwiązanie układu daje: Obliczamy pochodne występujace we wzorze na : Tworzymy funkcję: Zatem a tym samym funkcja f(x,y) ma w punkcie (1,-1) minimum warunkowe f(1,-1)=-1

Przykład-2 1 kg surowca A kosztuje 30 zł, 1 kg surowca B kosztuje 40 zł. Zysk ze sprzedaży stopu x kg towaru A i y kg towaru B określony jest wzorem: Dysponujemy kwotą 320 zł - ile należy zakupić surowca A a ile surowca B, aby zysk ze sprzedaży był największy. Zatem należy wyznaczyć maksimum warunkowe funkcji przy warunku czyli Mamy zatem: Tworzymy układ równań: Rozwiązanie układu daje: oraz Obliczamy pochodne występujace we wzorze : Tworzymy funkcję: Zatem a tym samym warunek konieczny nie rozstrzyga o istnieniu ekstremum. Zatem a tym samym funkcja f(x,y) ma w punkcie (1,-1) maksimum warunkowe f(8,2)=1024 Odp. Należy zakupić 8 kg surowca A i 2 kg surowca B

Omówione na przykładach funkcji 2 zmiennych kryterium jest szczególnym przypadkiem kryterium istnienia ekstremów związanych (warunkowych)

dla funkcji wielu zmiennych.

Twierdzenie o ekstremach związanych (warunkowych) w Rⁿ

Załóżmy że: Odwzorowanie g reprezentowane jest przez m funkcji: Szukamy punktów ekstremalnych związanych funkcji przy warunku będących punktami regularnymi odwzorowania g

Punkt dla którego nazywamy punktem regularnym zbioru jeżeli tzn. pochodna odwzorowania odwzorowuje przestrzeń R^n na całą R. Dla odzorowania zachodzi to wtedy i tylko wtedy gdy rząd macierzy jest równy m.

Warunek konieczny ekstremum związanego (warunkowego) Jeżeli funkcja f ma w punkcie regularnym ekstremum związane , to istnieje odwzorowanie liniowe takie że Odwzorowanie liniowe Λ nazywa się funkcjonałem Lagrange'a.

Uwagi do warunku koniecznego: Odwzorowanie liniowe jest reprezentowane w konkretnych bazach przestrzeni przez m liczb rzeczywistych a pochodna jest macierzą prostokatną o wymiarach m x n i rzędzie = m, zatem równania operatorowe i sprowadzają się do układu n+m równań skalarnych z n+m niewiadomymi : Rozwiązując ten układ otrzymamy współrzędne punktu podejrzanego o ekstremum lokalne związane. Liczby nazywane mnożnikami Lagrange'a, spełniają rolę pomocniczą,nie zawsze nas interesują i mogą być wyeliminowane przy rozwiązywaniu układu równań.

Warunek dostateczny ekstremum związanego (warunkowego) Niech teraz f,g będą dwukrotnie różniczkowalne : Jeżeli teraz forma kwadratowa: dla przyrostów takich że jest dodatnio określona to mamy minimum związane w P0 jest ujemnie określona to mamy maksimum związane P0 Mówimy wtedy że badamy formę kwadratową na przestrzeni stycznej

Uwagi do warunku dostatecznego: Problem sprowadza się zatem do zbadania formy kwadratowej: przy założeniu że: Ponieważ więc wyrażają się liniowo od pozostałych przyrostów gdzie jest pewną permutacją liczb 1,2,…,n. Mamy zatem: Wstawiając te zależności do formy kwadratowej n zmiennych: otrzymujemy formę kwadratową n-m zmiennych, którą badamy metodą wyznacznikową lub metodą wartości własnych.

Algorytm badania ekstremów związanych (warunkowych)

1. Tworzymy funkcję pomocniczą zwaną funkcją Lagrange'a

2. Rozwiązujemy układ n+m równań z n+m niewiadomymi

3. Znajdujemy punkty podejrzane o ekstremum P01 , P02 , P03 … eliminując mnożniki Lagrange'a

4. Sprawdzamy czy punkty podejrzane są punktami regularnymi zbioru tzn. czy dla każdego punktu podejrzanego P01 , P02 , P03 …

5. Znajdujemy postać wektorów dla których dla każdego punktu P01 , P02 , P03 … tzn. określamy przestrzenie styczne

6. Dla takich wektorów badamy określoność formy kwadratowej dla każdego punktu P01 , P02 , P03 …

7. Jeżeli teraz: dodatnio określona to mamy minimum związane ujemnie określona to mamy maksimum związane

Przykład Badamy ekstrema funkcji: związane warunkami:

1.Tworzymy funkcję Lagrange'a

2. Rozwiązujemy układ równań 5 równań z 5-cioma niewiadomymi:

3. Znajdujemy punkty podejrzane o ekstremum P01 , P02 , P03 … eliminując mnożniki Lagrange'a Z drugiego i trzeciego równania otrzymujemy rozwiązania: Dla rozwiązania otrzymujemy 2 punkty podejrzane: Dla rozwiązania otrzymujemy 2 punkty podejrzane:

4. Sprawdzamy czy punkty podejrzane są punktami regularnymi zbioru tzn.czy Określamy ogólną postać macierzy : Z postaci tej macierzy widać że dla każdego x,y,z dwa wiersze tej macierzy są liniowo niezależne zatem dla każdego punktu P01 ,P02 , P03,P04 czyli wszystkie punkty podejrzane są regularne.

5. Znajdujemy postać wektorów dla których dla każdego punktu P01 , P02 , P03, P04 tzn. określamy przestrzenie styczne

6. Dla takich wektorów badamy określoność formy kwadratowej dla każdego punktu P01 , P02 , P03, P04 a zatem mamy minimum związane (warunkowe) =-1 a zatem mamy również minimum związane (warunkowe) =-1

a zatem mamy maksimum związane (warunkowe) =5/4 a zatem mamy maksimum związane (warunkowe) =-3/4

Rozważymy teraz sposób określania ekstremów lokalnych funkcji uwiklanej dwóch zmiennych.Powstaje bowiem często pytanie: kiedy równanie F(x,y,z) = 0 określa funkcję dwóch zmiennych z = f(x,y) ?

Twierdzenie o istnieniu i jednoznaczności funkcji uwikłanej 2-zmiennych

Jeżeli { F(x,y,z) jest klasy C¹ w otoczeniu P0(x0, y0, z0) F(x0 , y0 , z0) = 0 F'z( x0 , y0 , z0) ≠ 0 } to wówczas { istnieje dokładnie jedna funkcja uwikłana z = f(x,y) określona lokalnie tzn. w pewnym otoczeniu punktu (x0 , y0) spełniająca warunek z0 = f(x0 , y0) } Wówczas funkcja z = f(x,y) jest klasy C¹ i jej pochodne cząstkowe:

Jeżeli dodatkowo F(x,y,z) jest klasy C² w otoczeniu P0(x0 , y0 , z0) to z = f(x,y) jest klasy C² w otoczeniu (x0 , y0) i jej drugie pochodne cząstkowe:

Ekstrema lokalne funkcji uwikłanej 2-zmiennych

Warunek konieczny istnienia ekstremum funkcji uwikłanej z = f(x,y): Wówczas pochodne cząstkowe II rzędu funkcji uwikłanej upraszczają się do postaci: Warunek dostateczny istnienia ekstremum: badanie określoności macierzy drugiej pochodnej dodatnio określona minimum lokalne ujemnie określona maksimum lokalne półokreślona (dodatnio,ujemnie) z definicji ekstremum nieokreślona nie ma ekstremum

Algorytm znajdywania ekstremów funkcji uwikłanej jednej zmiennej
1	Rozwiązujemy układ równań : Znajdujemy punkty podejrzane o ekstremum
2	W punktach sprawdzamy warunki istnienia funkcji uwikłanej oraz dwukrotnej różniczkowalności istniejącej funkcji uwikłanej
3	Obliczamy druga pochodną funkcji uwikłanej:
4	Sprawdzamy w punktach czy zachodzi któryś z warunków: to wówczas minimum lokalne funkcji uwikłanej to wówczas maksimum lokalne funkcji uwikłanej

Algorytm znajdywania ekstremów funkcji uwikłanej jednej zmiennej
1	Rozwiązujemy układ równań : Znajdujemy punkty podejrzane o ekstremum
2	W punktach sprawdzamy warunki istnienia funkcji uwikłanej oraz dwukrotnej różniczkowalności istniejącej funkcji uwikłanej
3	Obliczamy druga pochodną funkcji uwikłanej:
4	Sprawdzamy w punktach czy zachodzi któryś z warunków: to wówczas minimum lokalne funkcji uwikłanej to wówczas maksimum lokalne funkcji uwikłanej

Algorytm znajdywania ekstremów funkcji uwikłanej 2-zmiennych
1	Rozwiązujemy układ równań : Znajdujemy punkty podejrzane o ekstremum
2	W punktach sprawdzamy warunki istnienia funkcji uwikłanej z=f(x,y) oraz dwukrotnej różniczkowalności istniejącej funkcji uwikłanej
3	Obliczamy drugą pochodną funkcji uwikłanej przy uwzględnieniu warunku koniecznego:
4	Sprawdzamy w punktach czy zachodzi któryś z warunków: dodatnio określona minimum lokalne ujemnie określona maksimum lokalne półokreślona (dodatnio,ujemnie) z definicji ekstremum nieokreślona nie ma ekstremum

Przykład: Zbadajmy ekstrema funkcji uwikłanej Rozwiazujemy układ rownań : Rozwiazaniem sa dwa punkty oraz Sprawdzamy czy w tych punktach spełnione sa założenia twierdzenia o istnieniu funkcji uwikłanej Wszystkie pochodne cząstkowe I rzędu sa ciągłe wszedzie zatem F(x,y,z) jest klasy C¹ a ponadto: F(1,1,4)=0 F(-1,-1,-4)=0 F'z(1,1,4)=36≠0 F'z(-1,-1,-4)=-36≠0 Zatem w otoczeniu (1,1) istnieje gałąź jednoznaczna funkcji uwikłanej oraz w otoczeniu (-1,-1) istnieje gałąź jednoznaczna funkcji uwikłanej Sprawdzamy czy F(x,y,z) jest klasy C² : Są to funkcje ciągłe a więc F(x,y,z) jest klasy C² Ogólna macierz II pochodnej ma postać: a w punkcie (1,1,4) Minory główne Macierz II pochodnej jest ujemnie określona i mamy w punkcie (1,1) maksimum lokalne = 4. a w punkcie (-1,-1,-4) Minory główne Macierz II pochodnej jest dodatnio określona i mamy minimum lokalne = -4. Znajdziemy jeszcze gałęzie jednoznaczne funkcji uwikłanej.

Ekstrema globalne (wartość największa, wartość najmniejsza w zbiorze D)

Funkcja f(P) przyjmuje w punkcie P₀(x₀,y₀)єD minimum globalne jeżeli:

Funkcja f(P) przyjmuje w punkcie P₀(x₀,y₀)єD maksimum globalne jeżeli:

1	f(P) określona w obszarze otwartym D Jeżeli funkcja f(P) przyjmuje w punkcie wartość największą (najmniejszą) to w punkcie f(P) ma maksimum lokalne (minimum lokalne) Wniosek: funkcja określona w obszarze otwartym D może przyjmować ekstrema globalne jedynie w punktach ekstremów lokalnych a wówczas: - największe maksimum jest maksimum globalnym - najmniejsze minimum jest minimum globalnym Ponieważ jest to implikacja to w drugą stronę nie musi być prawdziwe tzn. - największe maksimum może nie być największą wartością funkcji - najmniejsze minimum może nie być najmniejszą wartością funkcji
2	f(P) określona w obszarze domkniętym f(P) może przyjmować ekstrema globalne: - w punktach ekstremów lokalnych wewnątrz obszaru - w punktach brzegowych obszaru
3	f(P) określona i ciągła w obszarze domkniętym i ograniczonym f(P) przyjmuje w obszarze wartość największą (kres górny) i najmniejszą (kres dolny) - w punktach ekstremów lokalnych wewnątrz obszaru - w punktach brzegowych obszaru

Przykład: Wyznaczymy największą i najmniejszą wartość funkcji w kole

Znajdujemy najpierw punkty krytyczne wewnątrz koła Układ równań ma jedyne rozwiązanie wewnątrz koła.

Szukamy punktów ekstremów globalnych na brzegu koła Z równania okręgu wyliczamy i wstawiamy do wzoru funkcji i otrzymujemy funkcję jednej zmiennej x którą oznaczymy przez g(x): Funkcja ta jest funkcją ciągłą w obszarze domkniętym a więc przyjmuje w tym obszarze wartość największą i najmniejszą w punktach krytycznych wewnątrz przedziału [-a,a] w punktach brzegowych przedziału [-a,a] Znajdujemy punkty krytyczne wewnątrz [-a,a] a wówczas czyli mamy punkty (0,a) i (0,-a) Zatem punktami w których może wystąpić ekstremum globalne są punkty: Tworzymy tabelkę wartości funkcji w tych punktach: P f(P) minimum globalne minimumglobalne maksimum globalne maksimum globalne

Optymalizacja funkcji

Optymalizacja jest to zagadnienie matematyczne polegające na znalezieniu najlepszego rozwiązania względem ustalonego kryterium (np. najmniejszych kosztów lub użytych zasobów, najkrótszej przebytej drogi) .

Podamy kilka przyładów optymalizacji dających się rozwiązać przy pomocy ekstremów lokalnych lub globalnych.

Przykład-1: Określić wymiary otwartego zbiornika prostopadłościennego (wanny) o danej objętości V tak aby jego pole powierzchni było jak najmniejsze a tym samym koszt zakupu materiałów potrzebnych do jego konstrukcji był minimalny. Przyjmujemy że wymiary podstawy wanny to x i y a jej wysokość to z. Wówczas objętość wanny V = xyz Pole powierzchni wanny S = 2yz+2xz+xy. W naszym zagadnieniu: x>0, y>0, z>0. Możemy przyjąć że mamy zbadać ekstremum funkcji S przy warunku dodatkowym V = xyz = constans wiążącym zmienne x, y i z. A więc zmienne x,y,z nie są niezależne zatem z tego równania możemy wyznaczyć z jako: Wówczas funkcja S jest funkcją 2 zmiennych: Obliczamy pochodne cząstkowe i przyrównujemy do zera: A zatem mamy jeden punkt krytyczny Liczymy pochodne cząstkowe II rzędu: A zatem macierz II pochodnej w punkcie krytycznym ma postać: Macierz II pochodnej jest dodatnio określona a zatem w punkcie mamy minimum lokalne. Wymiary optymalnego zbiornika dla ustalonej objętości V: Przykładowo dla objętości mamy wymiary:

Przykład-2 W równoramiennym trójkącie prostokątnym znaleźć punkt o tej własności że suma kwadratów jego odległości od wierzchołków trójkąta jest najmniejsza. Przyjmujemy wierzchołki trójkąta jako: A(0,0), B(a,0), C(0,a). Brzeg trójkąta możemy podzielić na 3 części: Część I: Część II: Część III: Obliczamy sumę kwadratów odległości punktu P(x,y) od wierzchołków A(0,0), B(a,0), C(0,a). Obliczamy pochodne cząstkowe I rzędu i znajdujemy punkty krytyczne Rozwiązanie daje jeden punkt krytyczny leżący we wnętrzu trójkąta. Poszukujemy teraz punktów na brzegu obszaru w których mogą występować ekstrema globalne. Analizę przeprowadzamy na każdej cząści brzegu trójkąta osobno. Część I: Funkcja f(x) jest ciągła na obszarze domkniętym a więc przyjmuje wartość najmniejszą i największą: wewnątrz przedziału [0,a] na brzegu przedziału w punktach x=0 lub x=a Określamy punkty krytyczne funkcji f(x) a zatem wewnątrz przedziału [0,a] mamy jeden punkt krytyczny oraz punkty końcowe przedziału [0,a]: Część II: Funkcja g(y) jest ciągła na obszarze domkniętym a więc przyjmuje wartość najmniejszą i największą: wewnątrz przedziału [0,a] na brzegu przedziału w punktach y=0 lub y=a Określamy punkty krytyczne funkcji g(y) a zatem wewnątrz przedziału [0,a] mamy jeden punkt krytyczny oraz punkt końcowy przedziału [0,a]: Punkt (0,0) wystąpił wcześniej więc go nie powtarzamy. Część III: Funkcja h(x) jest ciągła na obszarze domkniętym a więc przyjmuje wartość najmniejszą i największą: wewnątrz przedziału [0,a] na brzegu przedziału w punktach x=0 lub x=a Określamy punkty krytyczne funkcji h(x) a zatem wewnątrz przedziału [0,a] mamy jeden punkt krytyczny oraz punkty końcowy przedziału [0,a]: (0,a) i (a,0) ale one wystąpiły wcześniej więc ich nie powtarzamy. Budujemy tabelkę punktów w których mogą występować ekstrema i ich wartości. P f(P) Rodzaj ekstremum Minimum globalne Maximum globalne Maximum globalne Minimum globalne występuje w punkcie wewnętrznym trójkąta , który jest jego środkiem ciężkości.

Autor: Wojciech Drabik (PJWSTK)

15

---