I Wykład

WPROWADZENIE

Poszukiwanie minimum stosując metody poszukiwania w kierunku wygląda inaczej dla funkcji skalarnej i dla funkcji wielu zmiennych. O ile w przypadku f. skalarnej:

1. konieczne jest wyznaczenie błędu bezwzględnego określającego dokładność obliczeń,

2. zwykle znany jest przedział, w którym poszukujemy punktu ekstremalnego,

3. obliczenie pochodnej funkcji jest łatwe numerycznie,

o tyle w przypadku f. wielu zmiennych:

1. określamy dokładność względną obliczeń(ze wzgl. na wahania długości kroku obliczeń w

poszczególnych iteracjach),

2. przedział obliczeń nie jest zazwyczaj znany, jedynie znany jest często punkt brzegowy,

3. Wyznaczenie gradientu funkcji wielu zmiennych wymaga większej ilości obliczeń niż w

przypadku zadania jednowymiarowego.

Metody które będą przedstawione są metodami bezgradientowymi (rzędu zerowego) poszukiwania minimum w kierunku.

Zadanie optymalizacji dla zadania jednowymiarowego sprowadza się do znalezienia min. funkcji jednej zmiennej Q(x) klasy C¹ przy założeniu, że x ∈ [a,b]. Zakładamy, że funkcja ma w przedziale [a,b] pojedyncze minimum.

OPIS (IDEA) METOD

Zarówno metoda złotego podziału(nazywana również met. Złotego podziału odcinka) jak i metoda interpolacji kwadratowej Powella wymaga znajomości wartości Q(X) w trzech punktach przedziału [a,b].

METODA ZŁOTEGO PODZIAŁU - bezgradientowa

Jest to metoda geometryczna.

Założenia początkowe metody :

• ciągłość funkcji na rozpatrywanym przedziale [a, b],

• funkcja musi być unimodalna, co oznacza, że w przedziale [a, b] posiada tylko 1 punkt stacjonarny, który jest poszukiwanym minimum w kierunku,

• dla określenia podprzedziału przedziału [a, b], w którym leży punkt stacjonarny, należy obliczyć wartości funkcji w dwóch punktach tego przedziału

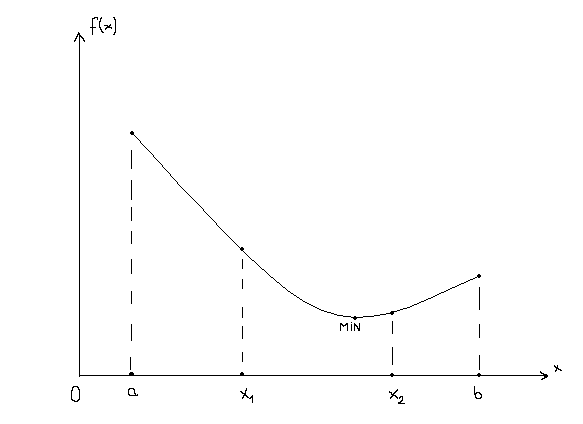
Polega na iteracyjnym zawężaniu przedziału, w którym znajduje się punkt optymalny. Na początku wyznaczamy 2 wartości x₁ , x₂ takie, że a< x₁< x₂<b. Korzystając z nierówności f(x₁)>f(x₂) możemy określić, w którym podprzedziale będzie się znajdował punkt optymalny, czy [x₁ ,b], czy [a, x₂]. Jeden z dwóch

wyznaczanych punktów x będzie zawsze znajdował się wewnątrz zredukowanego nowego podprzedziału, a tym samym w każdej następnej iteracji wystarczy obliczać wartość funkcji tylko w jednym punkcie. Aby usystematyzować wyznaczanie kolejnych podprzedziałów iteracji należy wprowadzić stały współczynnik α.

Skąd wzięła się nazwa złotego podziału ?

Do wyjaśnienia tego pojęcia pomocna będzie geometryczna konstrukcja nazwana właśnie „złotym podziałem odcinaka”.

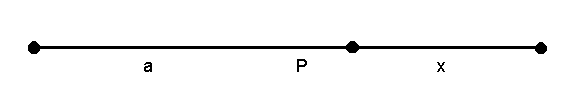
Odcinek podzielony jest punktem P w złoty sposób,
jeśli punkt P dzieli go na dwa odcinki: dłuższy i krótszy
w ten sposób, by krótszy miał się tak do dłuższego,
jak dłuższy do całego.

zgodnie z powyższym

przyjmując za a wartość 1 możemy wyznaczyć tzw. złotą liczbę. Rozwiązania tego równania to:

x=0,618034

Liczba ta nazywana jest w literaturze matematycznej małą złotą liczbą. Jest naszym szukanym współczynnikiem α.

Ciekawostka jest fakt, że odwrotność złotej liczby jest o 1 większa od niej samej. Ta liczba nazywana jest wielka złotą liczbą. Od czasów starożytnych złota proporcja jest uważana za najbardziej harmonijną. Architekci i rzeźbiarze greccy ściśle przestrzegali tej zasady w swojej twórczości.

METODA INTERPOLACJI KWADRATOWEJ POWELLA - bezgradientowa

Jest metodą aproksymacyjną.

Można ją stosować w celu przyspieszenia poszukiwania minimum Q(x) met. złotego podziału, gdy znane

jest dostatecznie małe otoczenie p. optymalnego [a_n, b_n], przy założeniu, że w otoczeniu punktu optymalnego [a_n, b_n] funkcję Q(x) można zastąpić wielomianem interpolacyjnym drugiego stopnia f(x).

Wartość funkcji jest obliczana w trzech kolejnych punktach, bowiem po zakończeniu każdej iteracji w met. złotego podziału znane są wartości w trzech kolejnych punktach: Q(x_a), Q(x_b), Q(x_c);

x_a < x_b < x_c(w pierwszej iteracji są to: Q(a₀), Q(l₀), Q(r₀) lub Q(l₀), Q(r₀), Q(b₀) ). Za pomocą tych punktów wielomianu osiąga minimum. Punkt ten z kolei zastępuje jeden z punktów początkowych i procedura jest powtarzana aż do spełnienia warunków zbieżności.

Algorytm metody złotego podziału

Podstawić za a₀ = a oraz b₀ = b. Mając przedział [a_i, b_i] określić zawężony przedział [a_i+1, b_i+1], wprowadzić punkty dodatkowe:

l_i = b_i - k(b_i - a_i)

r_i = a_i + k(b_i - a_i)

k - współczynnik złotego podziału; k = (pierwiastek 5 - 1)/2 ≈ 0,618

Jeżeli Q(l_i) > Q(r_i): a_i+1 = l_i; b_i+1 = b_i

Jeżeli Q(l_i) <= Q(r_i): a_i+1 = a_i; b_i+1 = r_i

Rozważamy więc podprzedziały [l_i, b_i] oraz [a_i, r_i].

< ilustracja działania >

Po n iteracjach x ∈ [a_n,b_n], przy czym: b_n - a_n = 0,618ⁿ(b-a)

Kryterium zbieżności

Dla n->∞: b_n - a_n -> 0 oraz b_i - a_i = k(b_i-1, a_i-1), więc odległość między punktami skrajnymi wewnątrz których znajduje się minimum, maleje liniowo w każdej iteracji. Mamy tu do czynienia ze zbieżnością liniową.

Warunkiem zakończenia działania algorytmu jest: |Δτ| < Δ, gdzie:

Δ - wymagana dokładność bezwzględna, przy czym Δ > 0,

Δτ = r_i - a = b - l_i = k²(b_i - a_i)

W algorytmie interpolacji kwadratowej zastosujemy wzór Powella, wynikający z interpolacyjnego wielomianu Lagrange'a.

Na podstawie obliczonych Q(x_a), Q(x_b), Q(x_c); x_a < x_b < x_c, wielomian interpolacyjny Lagrange'a przyjmuje postać:

(x - x_b)(x - x_c) (x - x_a)(x - x_c) (x - x_a)(x - x_b)

f(x) = Q_a --------------------- + Q_b --------------------- + Q_c ---------------------

(x_a - x_b)(x_a - x_c) (x_b - x_a)(x_b - x_c) (x_c - x_a)(x_c - x_b)

Algorytm metody interpolacji kwadratowej Polwella

Warunkiem koniecznym, a w naszym przypadku rónież wystarczającym instnienia min. jest:

df(x)

------ = 0 |

dx |x=x_m

Stąd:

2x_m - (x_b + x_c) 2x_m - (x_a + x_c) 2x_m - (x_a + x_b)

Q_a ------------------- + Q_b ------------------- + Q_C ------------------- = 0

(x_a - x_b)(x_a - x_c) (x_b - x_a)(x_b - x_c) (x_c - x_a)(x_c - x_b)

Czyli:

1 (x_b² - x_c²)Q_a + (x_c² - x_a²)Q_b + (x_a² - x_b²)Q_c

x_m = - ---------------------------------------------------

2 (x_b - x_c)Q_a + (x_c - x_a)Q_b + (x_a - x_b)Q_c

PODSUMOWANIE

Minimum można określić z żądaną dokładnością. Decydujący wpływ na efektywność algorytmu ma sposób doboru punktów wewnętrznych - metoda złotego podziału przewiduje zmniejszanie w każdej iteracji podprzedziału zawierającego minimum o stały czynnik k.

Metoda złotego podziału charakteryzuje się dużą prostotą oraz bardzo dobrą zbieżnością uzyskiwaną w każdej sytuacji. Wadą jest niewielka szybkość zbieżnośći, która jest tym mniejsza, im większą zakłada się dokładność obliczeń minimum w kierunku. Metoda ta przyjmuje słabe założenia(o ciągłości i istnieniu min. w kierunku).

Metoda interpolacji kwadratowej bazuje na bardziej zaostrzonych założeniach. Zaproponowana przez Powella idea wymaga ostrożności, gdyż znaleziony punkt może okazać się maksimum w kierunku. Ponadto niewłaściwa zmiana punktów wyjściowych może doprowadzić do niezbieżności, stąd wprowadza się szereg zabezpieczeń. Zaletą algorytmu jest natomiast najszybsza zbieżność.

---