7EKRAN_391
Lekcja 13-Analiza harmoniczna i stany nieustalone
Lekcja 13 zawiera wprowadzenie do analizy elektrycznych obwodów liniowych przy wymuszeniach niesinusoidalnych. W lekcji zaprezentowano listing programu zrealizowanego w środowisku Mathcad, pozwalającego na symulację analizy Fourierowskiej dla wybranych typów okresowych wymuszeń. W dalszej części lekcji przedstawiono zagadnienia stanów nieustalonych w obwodach na przykładzie liniowych obwodów I i II rzędu. Lekcje kończy procedura Odesolve programu Mathcad pozwalająca na rozwiązanie równania różniczkowego n-tego rzędu w tym nieliniowego budowa.
7EKRAN_392
Zgodnie z twierdzeniem Fouriera, jeżeli okresowa funkcja f(t) spełnia tzw. warunki Dirichleta to można ją przedstawić za pomocą sumy odpowiednich funkcji sinusoidalnych zwanych harmonicznymi oraz składowej stałej:
![]()
(1)
Dla k=0 tzw. harmoniczna zerowa zwana jest składową zerową-(stałą).
Komentarz-EKRAN_392
Warunki Dirichleta:
a)Funkcja powinna być jednoznaczna.
b)W dowolnym ograniczonym przedziale zmiennej niezależnej t funkcja może mieć skończoną liczbę maksimów i minimów.
c)W dowolnym ograniczonym przedziale t funkcja może mieć skończoną liczbę punktów nieciągłości, przy czym w każdym punkcie nieciągłości istnieją granice lewostronna i prawostronna, a wartość funkcji jest równa średniej arytmetycznej obu granic.
7EKRAN_393
Postać trygonometryczna szeregu Fouriera:
![]()
(2)
gdyż: ![]()
![]()
![]()
gdzie:
![]()
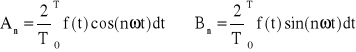
(3)
Komentarz-EKRAN_393
Postać (2) szeregu Fouriera jest często stosowana z powodu niedogodności wyznaczania amplitud Cn i kątów faz n kolejnych harmonicznych.
7EKRAN_394
Postać zespolona szeregu Fouriera:
Inną formą szeregu Fouriera, którą wykorzystano w programie symulacyjnym jest następująca postać zespolona szeregu Fouriera:
Niech:
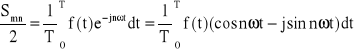
czyli: ![]()
Komentarz-EKRAN_394
Łatwo sprawdzić, że:
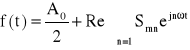
(4)
jest po prostych przekształceniach postacią tożsamą z ( 2).
7EKRAN_395
Postać wykładnicza szeregu Fouriera:
Można wykazać, że:
![]()
a stąd wzór (2) można przedstawić w postaci:·
![]()
(5)
7EKRAN_396
Jeżeli przyjmiemy, że:
![]()
zaś dla: ![]()
to wzór (5) można zapisać w postaci:
![]()
przy czym: ![]()
Komentarz-EKRAN_396
Dzięki liniowości obwodu stosując metodę superpozycji można analizować obwód klasyczną metodą symboliczną dla każdej harmonicznej z osobna sumując na końcu kolejne składowe obliczanego sygnału w postaci czasowej. Ponieważ „czysta” funkcja sinusoidalna w swoim rozkładzie może mieć tylko jedną harmoniczną, stąd analiza harmonicznych ma także ważne zastosowanie w ocenie stopnia odkształcenia przebiegu od sinusoidy.
7EKRAN_397
Wspólczynnik stopnia odkształcenia
Wykreślając ![]()
w funkcji częstotliwości otrzymamy tzw. widmo amplitudowe przebiegu okresowego zaś ![]()
w funkcji częstotliwości jest widmem fazowym.
Dla określenia ilościowego stopnia odkształcenia stosuje się obecnie wiele wskaźników, wśród, których nadal podstawowym jest tzw. współczynnik zniekształceń THD określony zależnością:
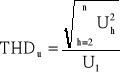
gdzie:
Uh - wartość skuteczna h-tej harmonicznej,
U1 - wartość skuteczna pierwszej harmonicznej (składowa podstawowa),
Komentarz-EKRAN_397
Wzór w liczniku zawiera wskaźnik liczby harmonicznych n. W zależności od stosowanych norm (lub morskiego towarzystwa klasyfikacyjnego) do obliczenia tego współczynnika stosuje się n = 40 lub n = 50.
7EKRAN_398
Przykład analizy liniowych obwodów przy wymuszeniach okresowych niesinusoidalnych metodą rozkładu w szereg Fouriera w środowisku Mathcad
Poniższy program pozwala na zasymulowanie okresowych niesinusoidalnych wymuszeń, które dalej są rozkładane na dowolne n- harmonicznych. W dalszym ciągu następuje analiza przykładowego obwodu elektrycznego z rysunku 1.
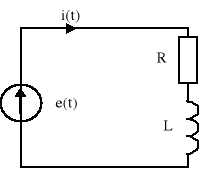
rys.1
7EKRAN_399
Start programu
Dane: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wpisz liczbę harmonicznych:
![]()
![]()
![]()
![]()
![]()
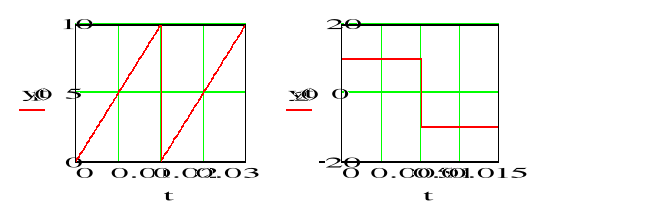
Komentarz-EKRAN_399
Funkcje od y1 do y5 są przykładowym przebiegami niesinusoidalnymi zdefiniowanymi za swój okres. Zmiana podstawienia w definicji funkcji g(t) powoduje automatyczne przeliczenie dla nowego wymuszenia. Na podstawie zdefiniowanych przykładów można zdefiniować dowolne funkcje wymuszające.
7EKRAN_400
![]()
![]()
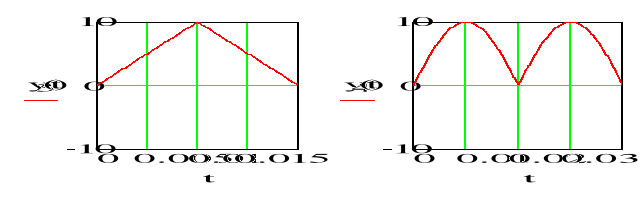
Komentarz-EKRAN_400
Użytkownik może oczywiście „kazać” programowi rozłożyć każdy dowolny przebieg (np. sinusoidę), dla którego będzie potrafił sformułować jego postać analityczną.
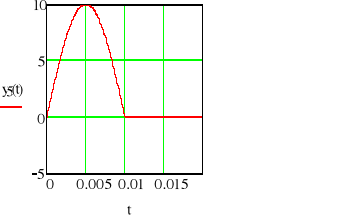
![]()
7EKRAN_401
Rozwiązanie
![]()
- wpisz żądaną funkcję w miejsce poprzedniej
![]()
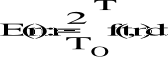
Em(n) - współczynniki szeregu Fouriera obliczone numerycznie, obok wartości dokładnych na podstawie wzoru analitycznego.


Komentarz-EKRAN_401
Wzór ![]()
został wyprowadzony z zespolonej postaci szeregu dla rozpatrywanej funkcji y1(t) (piłokształtnej).
7EKRAN_402
składowa stała:
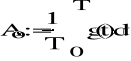
![]()

- Symboliczna postać szeregu Fouriera
![]()
![]()
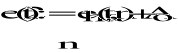
Komentarz-EKRAN_402
W celu otrzymania funkcji będącej sumą n uzyskanych harmonicznych (i składowej stałej, jeżeli nie jest równa zero) można wykorzystać dwie postacie: e(t) - tzw. postać symboliczną lub klasyczną sumę harmonicznych e2(t).
7EKRAN_403
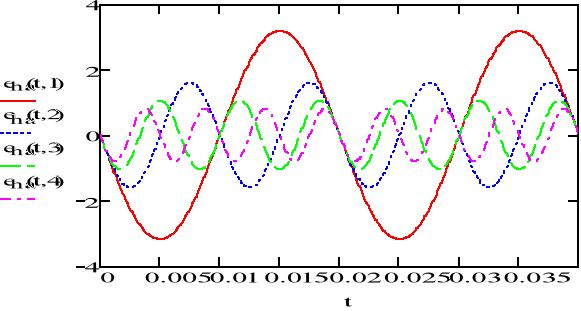
rys.2 Wybrane harmoniczne funkcji g(t)
7EKRAN_404
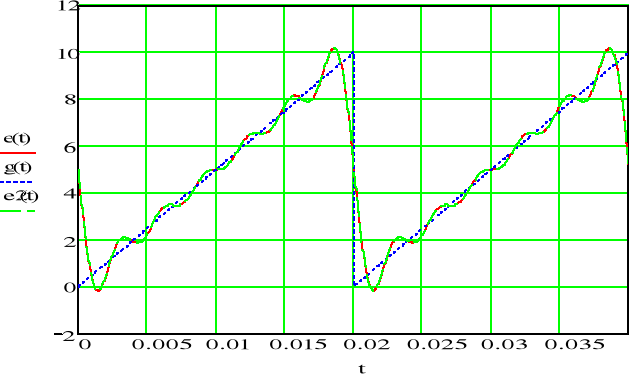
rys.3 Rozłożona funkcja na tle sumy jej n-harmonicznych
Komentarz-EKRAN_404
Widać, że rzeczywiście funkcja składająca się z harmonicznych (w tym przypadku n=6) zbliża się do rozkładanej funkcji piłokształtnej. Przy większej liczbie harmonicznych, można doprowadzić do graficznego pokrycia się obu przebiegów.
7EKRAN_405
Wartość skuteczna napięcia dla n harmonicznych:
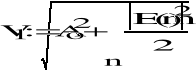
![]()
wartość dokładna z definicji: 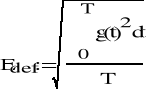
![]()
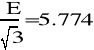
Procentowy względny błąd wartości skutecznej przy uwzględnieniu n-harmonicznych:
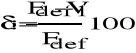
![]()
Komentarz-EKRAN_405
Można wyprowadzić następujący wzór określający wartość skuteczną przebiegu składającego się z n harmonicznych (wzór na V1 jest inną postacią wzoru: ![]()
gdzie E0 jest składową stałą oraz Ei wartością skuteczną i-tej harmonicznej.
W przypadku gdy znamy funkcję analityczną można obliczyć dokładną wartość skuteczną z definicji, stąd możemy określić błąd względny (z punktu widzenia wartości skutecznej) popełniany przy uwzględnieniu tylko n harmonicznych. Zauważ, że w rozpatrywanym przypadku dla n=6 harmonicznych błąd ten wyniósł zaledwie 1.174%.
7EKRAN_406
Współczynnik THD (Total Harmonic Distortion) i widmo amplitudowe.
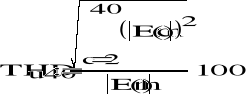
![]()
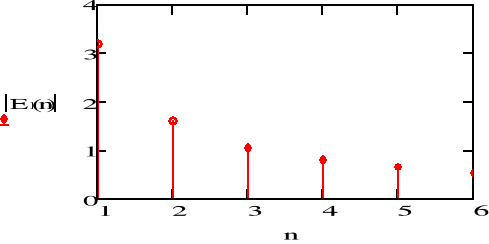
rys.4 Widmo amplitudowe napięcia dla n harmonicznych
Komentarz-EKRAN_406
W literaturze można spotkać się z innym wzorem na THD gdzie w mianowniku występuje nie pierwsza harmoniczna lecz całkowita wartość skuteczna. Takie podejście uniemożliwia osiągnięcie wartości THD powyżej 100% co jest możliwe dla bardzo odkształconych przebiegów w przypadku zastosowanego wzoru.
7EKRAN_407
Obliczenie harmonicznych prądu:
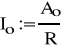
![]()
![]()

Wartość skuteczna dla n harmonicznych:
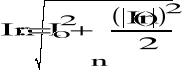
![]()
w
![]()
![]()
Komentarz-EKRAN_407
Stosując zasadę superpozycji można na podstawie harmonicznych wymuszenia ( w tym wypadku napięcia) wyznaczyć poszczególne harmoniczne odpowiedzi (i(t)). Ponieważ harmoniczne są funkcjami sinusoidalnymi stąd znajduje zastosowanie metoda symboliczna. Zwróć uwagę, że dla każdej harmonicznej zmienia się reaktancja zależna od pulsacji ![]()
7EKRAN_408
Wyznaczenie odpowiedzi prądowej na odkształcone wymuszenie napięciowe (suma harmonicznych):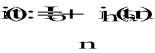
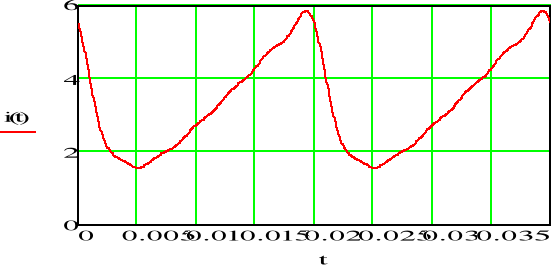
rys.5 Suma harmonicznych prądu
Komentarz-EKRAN_408
Możliwości komputerowe pozwalają na dodanie nawet wielkiej liczby harmonicznych i otrzymanie bardzo dokładnego przebiegu odpowiedzi. Należy pamiętać, że w przypadku wymuszeń innych niż sinusoidalnych ( nawet w obwodach liniowych) odpowiedź nie musi mieć analogicznego przebiegu. Np. w rozpatrywanym przypadku prąd (nawet dla dużej liczby harmonicznych) nie ma przebiegu piłokształtnego lecz raczej zniekształconą parabolę.
Obecnie powszechnie stosowanym narzędziem, do analizy harmonicznej przebiegów okresowych i nieokresowych są procedury FFT (Fast Fourier Transformation), oraz DFT (Discrete Fourier Transformation), które są również na wyposażeniu pakietu Mathcad. Zasadniczą zaletą powyższych procedur numerycznych jest możliwość dokonywania rozkładów funkcji danych w postaci zbioru punktów.
7EKRAN_409
Stany nieustalone
W obwodach elektrycznych pierwsze i drugie prawo Kirchhoffa jest spełnione dla wartości chwilowych prądów i napięć. Zatem w celu przeprowadzenia analizy obwodu, należy sformułować równania z funkcjami wartości chwilowych od czasu. Równania te są równaniami różniczkowymi liniowymi, zwyczajnymi, jeżeli rozpatrywany obwód jest liniowym obwodem o parametrach skupionych.
rys.6 Obwód RC I rzędu
Komentarz-EKRAN_409
W przypadku obiektu o tak zwanych parametrach rozłożonych, (np. w przypadku modelownia lini długiej, której nie można zastąpić pojedynczymi elementami skupionymi typu RLC) które zależą od zmiennej przestrzennej np. x, formułowanie równań Kirchhoffa z funkcjami chwilowymi prowadzi do równań różniczkowo cząstkowych.
7EKRAN_410
Jeżeli chcemy rozwiązać obwód z rys.6 po zamknięciu łącznika (komutacji) to na podstawie II prawa Kirchhoffa otrzymamy:
Uc(t) + i(t)R = e(t) (6)
Ponieważ ![]()
, a ładunek na kondensatorze q= CU
Zatem jeżeli C = const to i(t) = ![]()
stąd po podstawieniu do (6) otrzymamy ![]()
(7)
Komentarz-EKRAN_410
Równanie powyższe (7) jest równaniem różniczkowym liniowym o współczynnikach stałych, którego rozwiązanie otrzymujemy w dwóch etapach.
7EKRAN_411
Najpierw rozwiązujemy równanie jednorodne, czyli:
![]()
(8)
Równanie (8) jest równaniem o zmiennych rozdzielonych. Rozwiązanie ogólne (całka ogólna) równania jednorodnego (7) jest następująca:
![]()
.
Zgodnie z teorią równań różniczkowych liniowych rozwiązaniem ogólnym równania niejednorodnego (7) jest suma rozwiązania równania jednorodnego i funkcji (całki szczególnej) spełniającej całe równanie niejednorodne, czyli:
![]()
(9)
Komentarz-EKRAN_411
W celu znalezienia funkcji f(t) stosuje się takie metody jak metoda uzmienniania stałej w rozwiązaniu ogólnym równania jednorodnego, lub metody przewidywań. Równanie różniczkowe (7) sformułowane na podstawie II prawa Kirchhoffa musi być prawdziwe dla funkcji napięcia Uc(t) w każdej chwili czasu, a więc również po czasie nieskończenie długim. Stan taki nazywany jest stanem ustalonym, którego rozwiązanie łatwo znajdujemy dla takich wymuszeń jak sygnały stałe czy też sinusoidalne.
7EKRAN_412
Dla uproszczenia załóżmy, że e(t)=E. Zatem Uc(t)=E po czasie (teoretycznie) nieskończenie długim (kondensator naładuje się do wartości E źródła). Stąd rozwiązanie ogólne niejednorodnego równania różniczkowego (7) ma postać:
![]()
Jak widać rozwiązanie powyższe jest rodziną rozwiązań zależnych od stałej A. W celu określenia konkretnego przebiegu musimy znać jedną wartość poszukiwanej funkcji napięcia Uc(t).
Komentarz-EKRAN_412
Zazwyczaj wartościami początkowymi są: napięcie Uc(0) na kondensatorze lub prąd i(0) cewki. Jeżeli przez q(![]()
) oznaczymy ładunek na kondensatorze przed komutacją, a przez q(![]()
) po komutacji to musi być spełniony warunek:
q(![]()
)=q(![]()
)
gdyż skokowa zmiana ładunku prowadziłaby do nieskończonego wzrostu prądu ![]()
. Jeżeli założymy, że niemożliwa jest skokowa zmiana pojemności tzn. C = const. to z tego, że q = CU otrzymamy, że:
Uc(0-) = Uc(0+).
Mówimy wówczas o warunkach ciągłości napięcia na kondensatorze. Analogicznie wyprowadza się warunek ciągłości prądu w cewce przed i po komutacji wychodząc z ciągłości strumienia ![]()
. Przy założeniu, że indukcyjność cewki nie może zmienić się skokowo tzn. L=const., wówczas ![]()
a stąd otrzymujemy:
i(0-) = i(0+)
7EKRAN_413
Jeżeli w naszym przykładzie kondensator był wcześniej (przed komutacją) naładowany do jakiegoś napięcia Uc0, a zwrot tego napięcia był jak na rys.6 to warunkiem początkowym będzie Uc(0-) = -Uc0 = Uc(0+). Korzystając z warunku początkowego otrzymujemy równanie, z którego wyliczamy stałą A:
![]()
Zatem ostatecznym rozwiązaniem równania (1) jest.
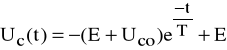
(10)
Komentarz-EKRAN_413
Występujące w rozwiązaniu T = RC nazywamy stałą czasową, której interpretacja graficzna jest przedstawiona na rys.7. Wartość stałej czasowej jest informacją o prędkości zanikania składowej swobodnej tzn. im T większe tym przebieg jest wolniejszy.

rys.7
7EKRAN_414
Przykład
Rozwiążemy obwód RL dla wymuszenia sinusoidalnego
Dane: e(t)=100sin(t+) L=1000mH R=1 Em=100V =314 =0
Równie różniczkowe ma postać: ![]()
(11)
Komentarz-EKRAN_414
Przypomnij sobie z lekcji 10 (ekran 266) , że napięcie na cewce ![]()
- jeżeli cewka jest liniowa, bezrezystancyjna i bezpojemnościowa.
7EKRAN_415
Na podstawie powyższych rozważań w obwodzie RC możemy przyjąć następujące uogólnienie. Dla jednorodnego równania różniczkowego o postaci:
![]()
Rozwiązaniem jest: ![]()
gdzie ![]()
Stąd rozwiązaniem ogólnym równania jednorodnego jest: ![]()
gdzie ![]()
Komentarz-EKRAN_415
Indeks p oznacza tzw. składową przejściową
7EKRAN_416
Zatem rozwiązaniem ogólnym równania (11) jest suma składowej przejściowej i ustalonej
![]()
Po rozwiązaniu stanu ustalonego metodą symboliczną otrzymano:
![]()
Ponieważ prąd przed zamknięciem łącznika nie mógł płynąć przez cewkę stąd na mocy warunku ciągłości uzyskujemy następujący warunek początkowy: i(0-)=i(0+).
Stąd ![]()
Po wyliczeniu z powyższego równania stała A=6.344.
Komentarz-EKRAN_416
Argument funkcji sinusoidalnej jest w mierze łukowej 1.507 [rad/s].
Jeżeli prąd w bardziej złożonym obwodzie przed komutacją nie jest równy zero to należy rozwiązać stan ustalony przed komutacją (metodą symboliczną) i z funkcji czasowej wyznaczyć wartość chwilową prądu i(0-) która będzie warunkiem początkowym dla równia różniczkowego.
7EKRAN_417
Ostateczne rozwiązanie równania (11) ma postać: ![]()
Funkcję tą zasymulowano w programie Mathcad:
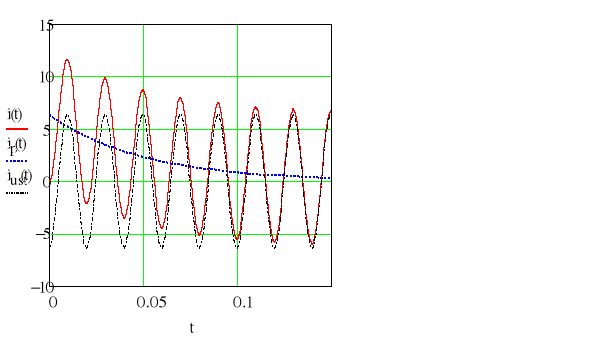
Komentarz-EKRAN_417
Zwróć uwagę, że największa wartość chwilowa stanu nieustalonego jest większa od amplitudy prądu. Stosunek tych wartości w przypadku prądu nazywamy przetężeniem. Można wykazać, że w liniowym obwodzie RL możliwe maksymalne przetężenie wynosi 2 i występuje dla fazy napięcia =0. Analogiczny stosunek napięć (największa wartość chwilowa do amplitudy) nazywamy przepięciem.
7EKRAN_418
Rozwiązanie obwodu II rzędu - RLC.
Rys.8
Na podstawie II prawa Kirchhoffa otrzymamy :
![]()
(12) ![]()
(13)
Po podstawieniu drugiego równania do pierwszego otrzymamy liniowe równanie różniczkowe rzędu drugiego:
![]()
(14)
Komentarz-EKRAN_418
Podobnie jak dla równania I rzędu, równanie powyższe analogicznie rozwiązujemy najpierw jako jednorodne, a następnie przewidując dowolną całkę szczególną (na przykład rozwiązując stan ustalony dla przebiegów stałych czy sinusoidalnych).
7EKRAN_419
Rozwiązaniem ogólnym całego równania będzie suma: Uc(t) = Ucsw(t) + Ucus(t)
Gdzie: Ucsw - składowa swobodna - rozwiązanie ogólne równania jednorodnego (15).
Ucus(t) - składowa ustalona - całka szczególna równania (14).
Rozwiązaniem poniższego równania jednorodnego (15).
![]()
(15)
jest: ![]()
(16)
Gdzie p1 i p2 to pierwiastki równania charakterystycznego: (17)
LCp2 + RCp + 1 = 0 (17)
Komentarz-EKRAN_419
Wzór 16 jest uniwersalny, aczkolwiek dla trzech różnych przypadków w zależności od wyróżnika równia 17, wygodniejsze są odrębne postacie wzoru (16).
7EKRAN_420
W zależności od wyróżnika powyższego równania rozróżnia się trzy przypadki:
1) ![]()
>0 zachodzi gdy ![]()
- wówczas pierwiastki p1 i p2 są rzeczywiste, a składowa swobodna ma przebieg aperiodyczny:
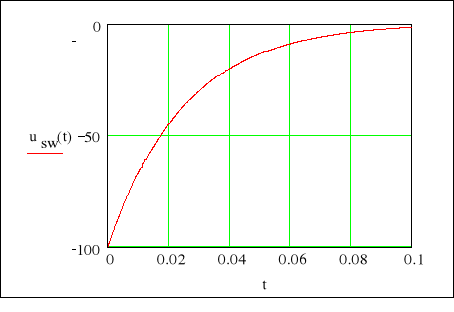
Przebieg aperiodyczny
Komentarz-EKRAN_420
Dla każdego innego obwodu opisanego liniowym równaniem różniczkowym o współczynnikach stałych, również zachodzą 3 przypadki zależne od
7EKRAN_421
2) ![]()
=0 zachodzi, gdy ![]()
wówczas p1 = p2 mówimy wtedy o najszybszym przebiegu aperiodycznym zwanym granicznym.
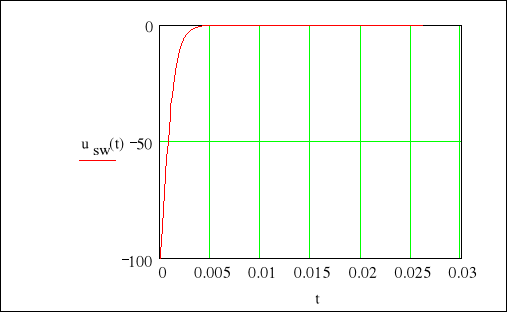
Przebieg aperiodyczny graniczny
7EKRAN_422
3) ![]()
<0 zachodzi, gdy ![]()
wówczas pierwiastki p1 i p2 są pierwiastkami zespolonymi sprzężonymi, a wykres składowej swobodnej, przedstawia przebieg oscylacyjny tłumiony (lub nietłumiony, gdy R = 0) o pulsacji drgań własnych:·
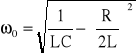
(18)
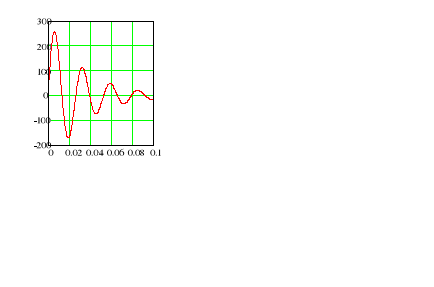
Przebieg oscylacyjny
Komentarz-EKRAN_422
Pierwiastki sprzężone mają postać 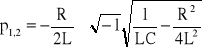
a w przypadku ogólnym ![]()
, gdzie (dla obwodu RLC) ![]()
jest tzw. współczynnikiem tłumienia. Zauważ, że dla R=0 ![]()
i przebieg przejściowy nie będzie tłumiony. Pulsacja drgań własnych jest wówczas nazywana pulsacją drgań swobodnych.
7EKRAN_423
Jeżeli wymuszenie e(t) jest funkcją sinusoidalną e(t) = Em sin(t + ) to całkę szczególną równania (14) najlepiej znaleźć jako rozwiązanie obwodu (rys.8) w stanie ustalonym - Ucust(t) = Umsin(t+). Wówczas rozwiązaniem ogólnym równania niejednorodnego jest:
![]()
(19)
W celu znalezienia stałych A1 i A2 korzystamy z warunków początkowych: Uc(0-) = Uc(0+) podstawiając do (19) oraz z iL(0-) = iL(0+) podstawiając do (19) po zróżniczkowaniu i pomnożeniu przez C (![]()
).Z tak otrzymanego układu równań obliczymy A1 i A2
Komentarz-EKRAN_423
Dla przypadku oscylacyjnego (p1 , p2 zespolone sprzężone) wygodniej jest rozwiązanie (19) przekształcić do następującej postaci czasowej (niezespolonej):
![]()
(20)
Gdzie U oraz 0 są stałymi wyznaczanymi na podstawie warunków początkowych.
7EKRAN_424
Przykład
Oblicz wartość napięcia na kondensatorze po czasie 4ms w układzie szeregowym RLC od momentu włączenia napięcia sinusoidalnego (rys.8). Przyjmij, że przed komutacją kondensator był nienaładowany.
Dane: R=10, L=100mH C=100F e(t)=100sin(t) V.
Komentarz-EKRAN_424
Odpowiedź: Napięcie na kondensatorze w 4ms wynosi uc(0.004)=36.872 V.
Przebiegi składowej swobodnej (przejściowej) ustalonej oraz ich sumy czyli stanu nieustalonego przedstawia poniższy rysunek:
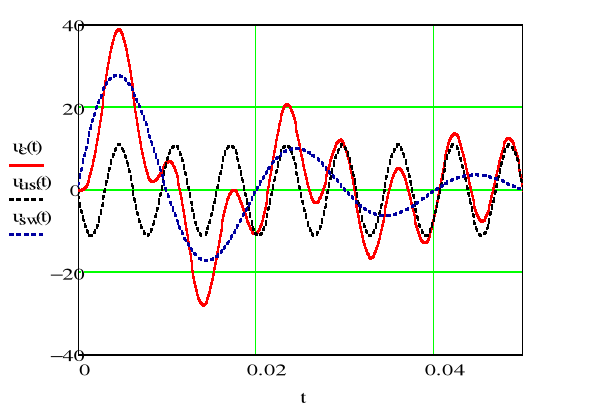
7EKRAN_425
Przykład wykorzystania gotowej procedury programu Mathcad (Odesolve) rozwiązującej dowolne równanie różniczkowe ( w tym nieliniowe)
Program Mathcad posiada szereg procedur numerycznych pozwalający rozwiązywać równania bądź układy równań różniczkowych. Jako przykład możliwości programu wybrano wygodną procedurę Odesolve.

Rys.9 Obwód zasilany napięciem sinusoidalnym z obciążeniem nieliniowym
Komentarz-EKRAN_425
Schemat na rys.9 przedstawia uproszczony model obwodowy zasilania z sieci okrętowej. Składa się on z siły elektromotorycznej, impedancji wewnętrznej reprezentującej sieć energetyczną oraz dławika nieliniowego z rezystancją, reprezentującego obwód nieliniowy.
Jako aproksymację nieliniowej charakterystyki strumienia wybrano funkcję![]()
, która spełnia wszystkie oczekiwane warunki: symetrię w I i III ćw., posiada pochodną w punkcie 0 oraz uwzględnia nasycenie (rys.10).
rys.10 Charakterystyka ![]()
7EKRAN_426
Równania różniczkowe dla układu przedstawionego na rys.9, z wykorzystaniem charakterystyki opisującej nieliniowość dławika![]()
, gdzie WL jest współczynnikiem można przedstawić następująco:
![]()
![]()
![]()
(21)
Komentarz-EKRAN_426
Otrzymane nieliniowe równanie różniczkowe w nie zmienionej postaci zostanie wpisane do procedury Odesolve w środowisku Mathcad.
7EKRAN_427
Start programu
Dane: ![]()
![]()
![]()
![]()
![]()
![]()

Warunek początkowy: ![]()
procedura num.: ![]()
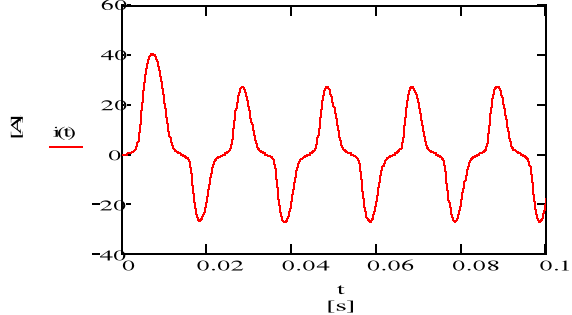
rys.11. Przebieg prądu
Komentarz-EKRAN_427
Procedura rozwiązania równania różniczkowego zaczyna się od słowa Given po którym wpisujemy równanie , a następnie nazwę procedury (odesolve) której argumentami są odpowiednio zmienna t, zakres obliczeń, oraz liczba kroków,
7EKRAN_428
![]()

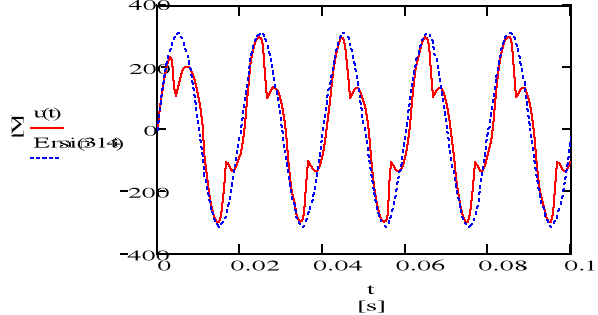
rys.12 Napięcie na zaciskach źródła - u(t) na tle idealnej siły elektromotorycznej źródła
Komentarz-EKRAN_428
Rozwiązanie równania stanu nieustalonego dla obwodu nieliniowego metodą numeryczną jest niekiedy jedyną możliwością obserwacji ( po kilku stałych czasowych) stanu ustalonego. W prezentowanym przykładzie można zaobserwować klasyczny przykład odkształcenia napięcia na szynach zasilających spowodowany nieliniowością odbioru.
7EKRAN_429
Podsumowanie
W niniejszej lekcji zapoznałeś się z podstawami analizy Fouriera bardzo ważnego narzędzia pozwalającego na identyfikacje i stopień odkształcenia sygnału od sinusoidy. Analiza harmoniczna jest powszechnie wykorzystywana nie tylko w elektrotechnice, ale w większości dziedzinach techniki jak również medycyny.
Z kolei badanie stanów nieustalonych przy załączaniu lub odłączaniu zasilania jest niezwykle istotne w elektrotechnice ze względu na możliwość występowania przepięć i przetężeń mogących doprowadzić do uszkodzeń w układzie jak i samego odbiornika. Jak pokazano w ostatnim przykładzie rozwiązując stan nieustalony w szerszym przedziale czasu można uzyskać przebieg stanu ustalonego dla np. obwodu nieliniowego. Otrzymany przebieg odkształcony może być z kolei poddany analizie harmonicznej na podstawie której wyznacza się współczynniki takie jak THD. Współcześnie, badanie odkształcenia zasilania sinusoidalnego jest powszechnym narzędziem w badaniu jakości energii elektrycznej.
t=0
i(t)
e(t)
L
R
Wyszukiwarka
Podobne podstrony:
m010p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Biochemia - kolokwium[1], Studia, Semestr III, Biochemia, Wykłady
m014a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m002b, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
02 Gelo ++, semestr I, Podstawy Prawa, Wykłady I semestr, egzamin, egzamin
ZASADA ZACHOWANIA PĘDU, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
zadania mechanika 11.06.2004, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m011p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Moment siły względem punktu, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
TOCZNE TARCIE LUX PROTOKOL, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m009a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
Wykład Antybiotyki 02, Licencjat, Semestr IV, mikrobiologia, Wykłady
m013a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m006a, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
macierzowa - ktatownica, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
TOCZNE TARCIE LUX, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
m013p, STUDIA, SEMESTR I, Mechanika, Mechanika Wyklady, Mechanika net
więcej podobnych podstron