EWA ELŻBIETA MAŁYSZKO

WSTĘP DO RÓWNAŃ RÓŻNICZKOWYCH CZĄSTKOWYCH

dla studentów studiów niestacjonarnych

Białystok 2009

SPIS TREŚCI

str.

Przedmowa…………………………………………………………………………..……..3

§1. Wstęp historyczny……………………………………………………………..……….4

§2. Całki ogólne równań różniczkowych cząstkowych……………………………………4

§3. Klasyfikacja równań różniczkowych cząstkowych, liniowych II rzędu z dwiema zmiennymi niezależnymi…………………………………..………………………………9

§4. Równania charakterystyk i sprowadzanie równań różniczkowych cząstkowych do postaci kanonicznej…………………………………………...…………………………..11

§5. Wyznaczanie rozwiązań równania falowego, spełniających dane warunki graniczne. Metoda Fouriera…………………………………………………………………………..14

PRZEDMOWA

Materiały te są przeznaczone dla studentów II semestru studiów niestacjonarnych Politechniki Białostockiej, kierunków: Inżynierii Biomedycznej i Elektrotechniki, jako uzupełnienie książki Jerzego Pietraszko Matematyka, teoria, przykłady, zadania, wydanej w Oficynie Wydawniczej Politechniki Wrocławskiej. Wymieniony podręcznik matematyki dla studentów 3-semestralnego kursu nie zawiera żadnych wiadomości o równaniach różniczkowych cząstkowych. Natomiast w wykładanym przez autorkę i innych pracowników naukowo-dydaktycznych Politechniki Białostockiej programie matematyki te zagadnienia obejmują kilka ostatnich wykładów.

E.E. Małyszko

§1. Wstęp historyczny

1. Rozwiązanie d'Alemberta.

Powstanie i rozwój teorii równań różniczkowych cząstkowych związane były z rozszerzeniem w XVIII wieku zakresu zastosowań analizy matematycznej funkcji wielu zmiennych. Były to zagadnienia z dziedziny astronomii, hydromechaniki, fizyki ciał sprężystych oraz geometrii.

Pierwszym problemem, rozwiązanym przy pomocy tych równań. było zadanie o drganiach struny.

W latach 1713-15 B. Taylor znalazł równanie małych drgań poprzecznych nieskończenie cienkiej, jednorodnej struny o długości l, umocowanej na końcach, wychylonej z położenia równowagi, a następnie pozostawionej samej sobie. Jednak dopiero około 1747 r. d'Alembert wyraził to, co Taylor sformułował językiem mechaniczno-geometrycznym, w postaci równania cząstkowego rzędu drugiego

gdzie
i
- to współrzędne punktu struny,
jest czasem, zaś
- stałym parametrem określającym gęstość struny i jej naprężenie.

W XIX wieku, po dokonanej klasyfikacji równań cząstkowych, nazwano to równanie falowym, lub równaniem typu hiperbolicznego.

Ogólne rozwiązanie tego równania dla
, przy warunkach brzegowych

i warunkach początkowych

znalazł d'Alembert za pomocą metody opartej na pojęciu różniczki zupełnej. Otrzymał rozwiązanie

i nazwał je rozwiązaniem ogólnym , gdzie
i
określić należy na podstawie warunków brzegowych i początkowych.

W późniejszym okresie d'Alembert proponował szukać rozwiązania w postaci iloczynu dwóch funkcji jednej zmiennej, tzw. metodą rozdzielenia zmiennych.

Ten pomysł szeroko rozwinął J.B. Fourier, na początku XIX wieku.

2. Rozwiązanie Eulera.

Rok po ukazaniu się prac d'Alemberta o strunie, L. Euler ogłosił artykuł „O drganiu strun” 1748, a potem w 1766 r. podał nową metodę rozwiązywania równania struny drgającej, która później weszła do wszystkich podręczników równań różniczkowych. Wprowadzając nowe współrzędne
przekształcił równanie falowe do postaci, którą łatwo jest scałkować:

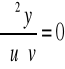
Euler pierwszy zrozumiał, że równanie struny drgającej jest obrazem procesu rozchodzenia się fal. Falą nazywamy przy tym proces przemieszczania się wzdłuż struny wychylenia jakiegokolwiek jej punktu. Euler dopracował do końca metodę d'Alemberta, którą później zaczęto nazywać metodą charakterystyk.

3. D. Bernoulli i rozwiązanie w formie szeregu trygonometrycznego.

Nowe i ważne twierdzenia o procesach drgających przedstawił w swoich rozprawach Daniel Bernoulli w latach 1747, 1748, 1753, 1755.

Ogólne rozwiązanie równania struny drgającej przedstawił on w postaci szeregu trygonometrycznego o współczynnikach nieoznaczonych.

gdzie
jest długością struny a
są funkcjami czasu.

4. Zadania hydromechaniki; równanie Laplace'a.

W Szkicu nowej teorii oporu cieczy Paryż 1752, d'Alembert - w związku z badaniem opływu ciała sztywnego przez jednorodną nieważką ciecz - rozwiązał zadanie, w którym chodziło o znalezienie dwóch funkcji p i q, mając ich różniczki zupełne

w ruchu płasko-równoległym cieczy, gdzie funkcje p i q są składowymi wektora prędkości cząstki cieczy w punkcie
płaszczyzny. D'Alembert doszedł do układu równań cząstkowych

,

Otrzymany układ scałkował stosując funkcje zespolone. Później, w 1761 r., w I tomie swych Dzieł matematycznych wskazał on, że funkcje
i
spełniają też równanie

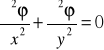
które nazwano później imieniem Laplace'a. Jego rozwiązania, mające ciągłe pochodne cząstkowe rzędów I i IIgo, nazwano później funkcjami harmonicznymi.

§.2 Całki ogólne w równaniach różniczkowych cząstkowych.

Definicja 1. Równaniem różniczkowym cząstkowym nazywamy równanie różniczkowe, w którym występuje funkcja niewiadoma dwóch lub więcej zmiennych i jej pochodne cząstkowe. Rzędem równania różniczkowego cząstkowego nazywamy największy rząd pochodnej funkcji niewiadomej występującej w danym równaniu.

Równanie różniczkowe postaci

jest równaniem rzędu drugiego, z niewiadomą funkcją dwóch zmiennych niezależnych.

Definicja 2. Rozwiązaniem ogólnym lub całką powyższego równania nazywamy każdą taką funkcję
, klasy
w pewnym obszarze
, która po podstawieniu wraz ze swymi pochodnymi do omawianego wyrażenia spełnia je tożsamościowo.

Zadania

a) Sprawdź, czy funkcja
jest rozwiązaniem równania różniczkowego

b) Wyznaczyć ogólne rozwiązanie równania

całkując równanie stronami względem
, a potem względem
.

c) Wyznaczyć ogólne rozwiązanie równania

Odpowiedzi do zadań

1. tak

2. 
   gdzie
   

3. 
   

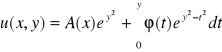
§3. Klasyfikacja równań różniczkowych liniowych cząstkowych II rzędu z dwiema zmiennymi niezależnymi.

Definicja. Równaniem różniczkowym cząstkowym liniowym rzędu drugiego o niewiadomej funkcji
dwóch zmiennych niezależnych
i
nazywamy równanie postaci

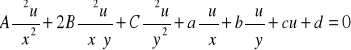
gdzie
są danymi funkcjami dwóch zmiennych
i
o ciągłych pochodnych w pewnym obszarze płaskim
.

Własność. Znak wyrażenia
nie ulega zmianie przy nieosobliwym przejściu do innych zmiennych niezależnych, dzięki czemu klasyfikuje się równania tego typu ze względu na znak
w następujący sposób:

a)
- równanie jest hiperboliczne

b)
- równanie jest paraboliczne

c)
- równanie jest eliptyczne.

Uwaga. W przypadku, gdy dane jest równanie liniowe, jednorodne, cząstkowe rzędu drugiego o współczynnikach stałych, to można sprowadzić je do postaci kanonicznej, czyli

c)
- równanie Laplace'a

a) lub
- równanie struny (falowe)

b) lub
- równanie przewodnictwa cieplnego.

Zadanie

Wyznaczyć obszary, w których zachowuje się typ równania

a)

b)

c)

d)

e)

f)

Odpowiedzi do zadania.

1. równanie jest eliptyczne w półpłaszczyźnie
   i
   , hiperboliczne w półpłaszczyźnie
   i
   ; paraboliczne na prostych
   i
   

2. równanie jest eliptyczne w półpłaszczyźnie
   , hiperboliczne w półpłaszczyźnie
   , paraboliczne na prostej
   

3. równanie jest eliptyczne w półpłaszczyźnie
   i
   , hiperboliczne w płaszczyźnie
   i
   , paraboliczne na prostych
   i
   

4. równanie jest eliptyczne w I lub II ćwiartce płaszczyzny
   , hiperboliczne w II lub IV ćwiartce płaszczyzny
   , paraboliczne na prostych
   oraz
   

5. eliptyczne w obszarach
   lub
   , hiperboliczne w obszarach (x < y)
   (x > 0) lub (x < 0)
   (y > 0) lub (y < 0)
   (x > 0) lub (y < x)
   (x < 0), paraboliczne na prostych
   oraz
   

6. równanie jest eliptyczne w obszarach
   lub
   , hiperboliczne w obszarach
   , paraboliczne na prostej
   oraz na paraboli
   .

§4. Równania charakterystyk i sprowadzanie równań różniczkowych cząstkowych do postaci kanonicznej.

Definicja. Charakterystykami omówionego wyżej równania nazywamy krzywe całkowe równania różniczkowego zwyczajnego

Gdy
, to

rozwiązania tych równań oznaczamy
. Aby sprowadzić omawiane równanie do postaci kanonicznej, należy podstawić za nowe zmienne

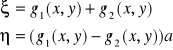
gdzie
w przypadku gdy

oraz
w przypadku

W przypadku gdy
, istnieje tylko jedna rodzina charakterystyk o równaniu
.Wtedy podstawiamy

,
(lub

Dobieramy podstawienie tak, by
.

Oznaczmy teraz: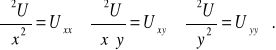

Przykład. Wyznaczyć charakterystyki równania

Rozwiązanie. Charakterystyki spełniają równanie

Rozwiązując równanie kwadratowe, otrzymamy

lub
lub

stąd mamy charakterystyki:

lub

Zadanie

Wyznaczyć charakterystyki równania:

a)

b)

c)

d)

e)

Odpowiedzi do zadania

a)
,

b)
,

c)

d)
,

e)

§5. Wyznaczanie rozwiązań równania falowego spełniających dane warunki graniczne. Metoda Fouriera.

Przykład. Znaleźć rozwiązanie szczególne
równania różniczkowego falowego
, spełniające warunki graniczne:

brzegowe: 1)
, 2)

i początkowe: 3)
, 4)

Funkcja
opisuje położenie struny drgającej. Zmienna
- czas.

Aby uprościć zapis oznaczamy odtąd
oraz

Rozwiązanie. Szukamy (w myśl metody Fouriera) rozwiązań danego równania w postaci iloczynu dwóch funkcji, jednej zależnej tylko od
, a drugiej tylko od
.

Obliczamy jej pochodne cząstkowe II rzędu.

,

,

Podstawiamy je do równania falowego.

Następnie rozdzielamy zmienne.

, gdzie
jest pewną stałą.

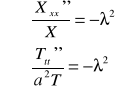
Są to dwa równania różniczkowe zwyczajne, jednorodne, o stałych współczynnikach.

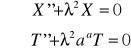
Funkcje te są całkami ogólnymi obu tych równań różniczkowych zwyczajnych.
są stałymi całkowymi dowolnymi. Podstawiamy je do postaci iloczynowej rozwiązania równania falowego.

Wartości stałych wyznaczamy z warunków granicznych.

Warunek 1)
, daje

oraz
bo

Warunek 2)
, daje

stąd
.

Podstawiam
i mam
, dla
,

Każdej liczbie
tej postaci odpowiada rozwiązanie szczególne postaci

oznaczamy
,
- dowolne stałe

Ponieważ wyjściowe równanie jest liniowe, więc nawet nieskończona suma jego rozwiązań jest też rozwiązaniem, w postaci szeregu trygonometrycznego.

też jest rozwiązaniem spełniającym warunki początkowe 1), 2).

Aby wyznaczyć stałe
i
wykorzystamy dwa pozostałe warunki graniczne.

Podstawiamy
,
do równości w postaci szeregu trygonometrycznego, otrzymamy

Następnie różniczkując względem
rozwiązanie w postaci szeregu, mamy

tu podstawiamy
,
, otrzymując

Powyższe równości przedstawiają rozwinięcia funkcji
,
w przedziale
w niepełny szereg Fouriera zawierający tylko sinusy. Współczynniki tych rozwinięć określone są wzorem:

jeśli
, to

na podstawie tych wzorów otrzymamy

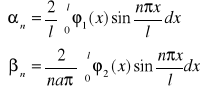
Odpowiedź. Rozwiązaniem szczególnym spełniającym dane warunki graniczne będzie funkcja w postaci szeregu Fouriera wraz ze stałymi
,
określonymi powyższymi wzorami.

Zadanie

Rozwiązać zagadnienie graniczne dla równania
przy następujących warunkach:

a)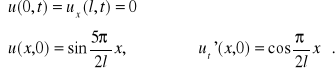

b)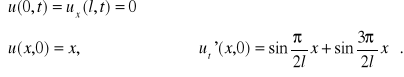

c)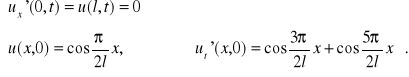

Odpowiedzi do zadania

a)

b)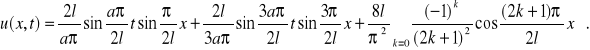

c)

1

---