Pytania na egzamin testowy z matematyki dla I-go roku KNEiS (semestr II).
1. Funkcje wielu zmiennych (granica funkcji), pochodne kierunkowe i pochodne cząstkowe funkcji, gradient funkcji i różniczkowalność funkcji.
Funkcje wielu zmiennych
Funkcją n - zmiennych x = (x1,x2,...,xn) nazywamy funkcję f: Rn → R (piszemy f(x) = f(x1,x2,...,xn)), np.:
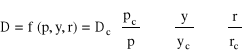
- funkcja wielkości popytu
p - cena towaru
y - dochód „per capito” (na osobę); α, β, γ, pc, yc, rc, Dc - stałe
r - wydatki na reklamę
Funkcja wielkości produkcji
p = f (K,L) ; K - kapitał zainwestowany, L - wielkość zatrudnienia (w roboczogodzinach)
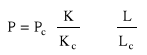
; Pc - wielkość produkcji osiągana dla kapitału K = Kc i zatrudnienia L = Lc
Granica funkcji
Niech f :![]()
Liczba g∈R jest granicą funkcji „f” w punkcie x0 (piszemy ![]()
)
Heinego
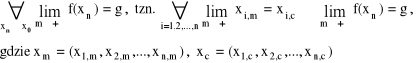
Cauchy'ego
![]()
Pochodną kierunkową funkcji f: Rn → R w punkcie x0∈Rn w kierunku wektora a = [a1,a2,...,an]∈Rn nazywamy granicę:
![]()
Pochodną cząstkową
![]()
nazywamy pochodna kierunkową funkcji f w kierunku wektora ei = [0,0,...,0,1,0,...,0], tzn.
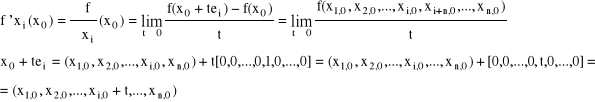
Gradientem (pochodną) funkcji f w punkcie x0 nazywamy wektor:
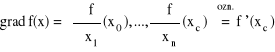
Różniczkowalność funkcji
![]()
gdzie ![]()
oraz 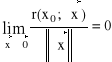
2. Pochodne cząstkowe wyższych rzędów, różniczki wyższych rzędów, tw. Schwarza, wzór Taylora.
Pochodne cząstkowe rzędu drugiego
Niech f posiada pochodna cząstkową ∂f / ∂xi w otoczeniu K(x0, r) punktu x0. Jeśli funkcja ∂f / ∂xi posiada ponadto pochodną cząstkową po xj, to nazywamy ją pochodna cząstkową rzędu drugiego i oznaczamy:
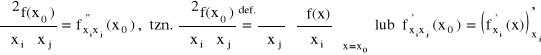
Uwaga: Jeśli i = j, to piszemy 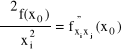
Różniczka rzędu drugiego
Różniczką zupełną rzędu drugiego nazywamy różniczkę różniczki rzędu pierwszego, tzn.:
![]()
Tw. Schwarza
Zał.: Funkcja f posiada ciągłe pochodne mieszane: ![]()
w otoczeniu punktu x0
Teza: 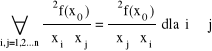
3. Def. ekstremum funkcji, warunki konieczne i dostateczne na ekstremum.
Ekstremum funkcji
Niech f: D ⊂ Rn → R, x0∈D nazywamy:
1) maksimum ⇔ ![]()
2) minimum ⇔ ![]()
Warunek konieczny na ekstremum
Zał. 1) f: D ⊂ Rn → R, x0∈D
2) f jest różniczkowalna w x0
3) x0 - ekstremum lokalne (minimum lub maksimum)
Teza f '(x0) = grad f(x0) = ![]()
, tzn. ![]()
, czyli ![]()
dla i = 1,2,...,n
Warunki dostateczne na ekstremum
Zał. 1) f: D ⊂ Rn → R, f posiada w otoczeniu punktu x0 (K(x0,E)⊂D) ciągłe pochodne cząstkowe do rzędu drugiego (włącznie): ![]()
2) f '(x0) = grad f(x0) = ![]()
Teza 1) Jeśli d2f(x0) (czyli f ''(x0)) jest dodatnio określona to x0 jest minimum lokalnym
2) Jeśli d2f(x0) (czyli f ''(x0)) jest ujemnie określona to x0 jest maksimum lokalnym
3) Jeśli d2f(x0) nie jest określona to x0 nie jest ekstremum
4) Jeśli d2f(x0) jest półokreślona to x0 może być lub nie ekstremum lokalnym
4. Ekstremum warunkowe, funkcja Lagrange'a, warunki konieczne i dostateczne.
Ekstremum warunkowe
Mówimy, że funkcja „f” ma w punkcie x0∈M maksimum (minimum) lokalne związane (warunkiem M lub na powierzchni M) jeśli:
![]()
Uwaga: Zamiast o maksimum (minimum) lokalnym związanym, mówimy tez o maksimum (minimum) lokalnym warunkowym przy warunku ![]()
Funkcja Lagrange'a
Funkcję L: D ⊂ Rn → R określoną następująco: ![]()
, gdzie λ = [λ1, λ2,..., λm], λi∈R (i = 1,...,m) nazywamy funkcją Lagrange'a dla problemu ekstremum warunkowego zadanego funkcją „f” oraz funkcjami g1, g2,..., gm. Stałe λi (i = 1,...,m) nazywają się mnożnikami Lagrange'a lub czynnikami nieoznaczonymi Lagrange'a.
Warunek konieczny na ekstremum warunkowe
Zał. Jeśli f,g1,...,gn mają ciągłe pochodne cząstkowe rzędu pierwszego w otoczeniu x0, x0 jest punktem regularnym zbioru M oraz f posiada w x0 ekstremum warunkowe gc przy warunku M
Teza: Istnieją stałe ![]()
takie, że:
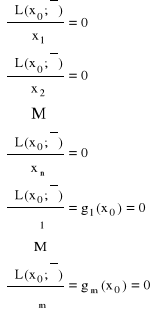
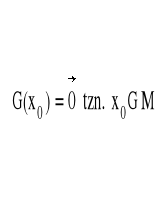
Warunki dostateczne istnienia ekstremum warunkowego
Zał. (1) Funkcje f,g1,g2,...,gm posiadają pochodne cząstkowe do rzędu II-go włącznie na zbiorze D⊂Rn (D - otoczenie)
(2) x0 jest punktem regularnym zbioru M
(3) x0 spełnia równania Lagrange'a: ![]()
(jest to warunek konieczny)
Teza: (1) Jeśli forma kwadratowa ![]()
zadana macierzą ![]()
jest dodatnio (ujemnie) określona na zbiorze ![]()
, tzn.:
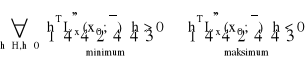
to x0 jest minimum (maksimum) warunkowym
(2) Jeśli forma kwadratowa ![]()
nie jest określona, to x0 nie jest ekstremum warunkowym
5. Metoda najmniejszych kwadratów.
Metoda najmniejszych kwadratów
Przypuśćmy, że mamy n - punktów na płaszczyźnie P1(x1,y1), P2(x2,y2),..., Pn(xn,yn). Poszukujemy funkcji f = f(x) należącej do pewnej klasy F, np. F = {f; f(x) = ax + b} takiej, że wyrażenie ![]()
jest najmniejsze. Wielkość ![]()
wyraża odległość punktu Pi(xi,yi) od punktu wykresu (xi,f(xi)) funkcji f.
d2 • Pn
• P1 • •
• d1 • P2 • P3 dn X
• d3
• d4
• P4
X
Zatem wybieramy funkcję z danej klasy tak, aby wielkość ![]()
była najmniejsza.
Efektywne wzory podamy dla klasy funkcji liniowych: F = {f: R → R; f(x) = ax + b}
Niech ![]()
. S osiąga minimum dla wartości ![]()
takich, że:
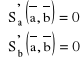
• P3 • dn ![]()
• d3 • Pn
• P1 • d2
• d1 • P2
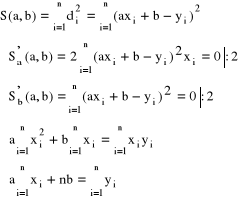
Stosujemy wzory Cramera:

Ostatecznie:
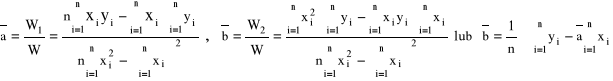
b2 b
b2 b
b2i bi
<a;b〉 Pi
a2
a a2i ai
a1 b1 a2 a
a1 a1i b1i b1
6. Całka Riemana funkcji wielu zmiennych (ciąg podziałów normalnych przedziału w R2, sumy Riemana, sumy dolne i górne, całka dolna i górna Darboux, całkowalność funkcji w sensie Riemana), całka z funkcji po dowolnym zbiorze ograniczonym.
Całka Riemana funkcji wielu zmiennych na przedziale <a;b〉 (prostokącie)
Niech <a;b〉 = <a1;b1〉 × <a2;b2〉, gdzie a = (a1,a2), b = (b1,b2)
Podziałem przedziału <a;b〉 nazywamy zbiór prostokątów: Π = {Pi}i = 1,2,...,n , n = n1 · n2; <a;b〉 = ![]()
![]()
Polem (miarą) przedziału Pi nazywamy liczbę
![]()
Ciąg przedziałów Π(n) = {Pi(n)}i = 1,2,...,n nazywamy ciągiem przedziałów normalnych przedziału <a;b〉 jeśli
![]()
Sumy Riemana
Niech f: <a;b〉 → R, f - ograniczona na <a;b〉.
Sumą całkowitą Riemana funkcji f dla przedziału Π = {Pi} nazywamy sumę:
![]()
, gdzie ![]()
Suma dolna Suma górna
![]()
, gdzie ![]()
![]()
, gdzie ![]()
Całkowalność funkcji w sensie Riemana
Funkcję „f” nazywamy całkowalną w sensie Riemana na przedziale <a;b〉, jeśli dla każdego ciągu przedziałów normalnych Πn = {Pi(n)}i = 1,2,...,n , n∈N i przy dowolnym wyborze punktów ξi(n)∈Pi(n) , ciąg sum Riemana jest zbieżny.
![]()
Granicę tą nazywamy całką Riemana na przedziale <a;b〉 i oznaczamy:
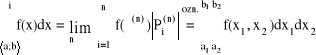
Całką dolną Darboux nazywamy kres górny sum dolnych:
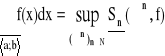
Całką górną Darboux nazywamy kres dolny sum górnych:
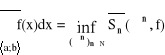
Całka z funkcji po dowolnym zbiorze ograniczonym
Niech A ⊂ Rm, A ⊂ <a;b〉 ⊂ Rm; f<a;b〉 → R
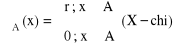
- funkcja charakterystyczna zbioru A
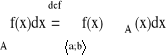
Uwaga:
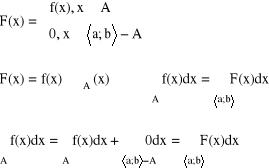
7. Własności całki Riemana, wzór Fubiniego, całkowanie po zbiorach normalnych.
Własności całki Riemana
Zał. f - ciągła i ograniczona na zbiorze A
Teza Istnieje całka: ![]()
A = A1 ∪ A2 , A1 ∩ A2 = ∅ ⇒
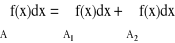
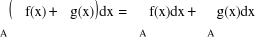
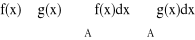
Tw. Fubiniego
Zał. 1) A = A1 × A2 ⊂ Rk + m, A1 ⊂ Rk , A2 ⊂ Rm
Zbiór A jest ograniczony, f: A = A1 × A2 → R, f = f(x,y), x = (x1,...,xn) ⊂ A1, y = (y1,...,ym) ⊂ A2
f - ograniczona na zbiorze A
2) f - całkowalna na zbiorze A, tzn.:![]()
- istnieje
Teza: ![]()
istnieje ![]()
oraz ![]()
istnieje ![]()
![]()
Funkcje Ρ i Ψ są całkowalne na zbiorach A1 i A2 oraz zachodzi równość:
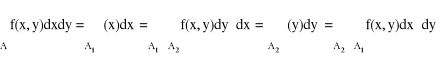
A1 = <a,b〉 ⊂ R
A2 = <c,d〉 ⊂ R
d
A2 A
c
a A1 b X
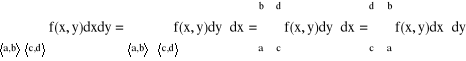
Wniosek:
a = (a1,...,an), b = (b1,...,bn)
A = <a,b〉 = <a1,b1〉 × <a2,b2〉 × ... × <an,bn〉
Całkowanie po zbiorach normalnych
Zał. f = f(x,y) - ciągła na zbiorze normalnym względem osi OX lub osi OY
Teza 1) Jeśli A = {(x,y); a ≤ x ≤ b, g1(x) ≤ y ≤ g2(x)} to:
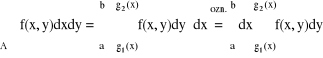
2) Jeśli A = {(x,y); c ≤ y ≤ d, h1(y) ≤ x ≤ h2(y)} to:
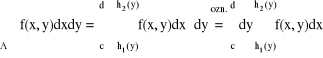
8. Wzór na zamianę zmiennych, współrzędne biegunowe, współrzędne walcowe i współrzędne sferyczne, stosowanie tych współrzędnych do wzoru na zamianę zmiennych.
Tw. o zamianie zmiennych
Zał. 1) Niech g: A ⊂ Rm → g(A) ⊂ Rm, y = g(x) = [g1(x),...,gm(x)], x = (x1,...,xm) ∈ A
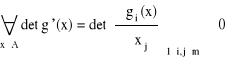
(tzn. g jest regularne na zbiorze A)
2) f - całkowalna na zbiorze g(A)
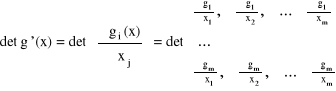
det g '(x) - jacobian (wyznacznik macierzy Jacobiego)
Teza ![]()
lub: g: g-1(B) → B ⊂ Rm to ![]()
Współrzędne biegunowe na płaszczyźnie
Dla n = 2 przyjmujemy oznaczenia: x = (x1,x2)![]()
(x,y) - współrzędne kartezjańskie punktu P(x,y)
Parę liczb (γ,ϕ), gdzie γ∈(0;+∞), ϕ∈<0;2Π〉 nazywamy współrzędnymi biegunowymi, jeśli ![]()
oraz:
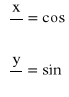
tzn.: 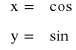
Y
y P(x,y)
γ
ϕ
x X
Uwaga: x2 + y2 = r2cos2ϕ + r2sin2ϕ = r2(cos2ϕ + sin2ϕ) = r2 ⇒ x2 + y2 = r2
Współrzędne walcowe
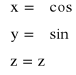
(γ,ϕ,z) - współrzędne walcowe
g(γ,ϕ,z) = (γ cosϕ, γ sinϕ, z) = (x,y,z)
det g '(γ,ϕ,z)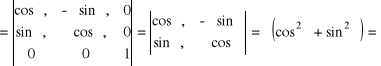
W = {(x,y,z); x2 + y2 ≤ a2, 0 ≤ z ≤ h} - walec o podstawie kołowej i wysokości h
W = {(γ,ϕ,z); 0 ≤ γ ≤ a, 0 ≤ ϕ ≤ 2Π, 0 ≤ z ≤ h}
![]()
z
h
a Y
X
Współrzędne sferyczne
(γ,ϕ,ψ) ![]()
ϕ∈<0,2Π〉 ψ∈<0,Π〉
z
(x,y,z)
ψ γ ψ
y
γ '
ψ
(x,y,0)
![]()
x = γ · cos ϕ · sin ψ
y = γ · sin ϕ · sin ψ
z = γ · cos ϕ
Niech g(γ,ϕ,ψ) = (γ · cos ϕ · sin ψ, γ · sin ϕ · sin ψ, γ · cos ϕ) = (x,y,z)
det g '(γ,ϕ,ψ) = 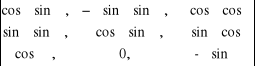
=
= γ2 sin ψ (- cos2ϕ sin2ψ - sin2ϕ cos2ψ - cos2ϕ cos2ψ - sin2ϕ sin2ψ) =
= - γ2 sin ψ (cos2ϕ (sin2ψ + cos2ψ) + sin2ψ (cos2ψ + sin2ψ) = - γ2 sin ψ
![]()
9. Całki niewłaściwe, wzór na zamianę zmiennych, wprowadzenie całki Gaussa.
Całki niewłaściwe
Zakładamy, że ![]()
f - całkowalna na zbiorze An. Mówimy, że całka z funkcji f = f(x) na zbiorze A istnieje (jest zbieżna), jeśli istnieje, przy dowolnym wyborze ciągu An, skończona granica: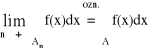
Tw. o zamianie zmiennych
![]()
, gdzie A = {(x,y); x ≥ A; y ≥ A}
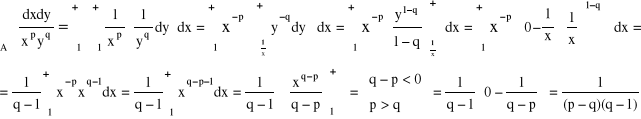
dla p > q > 1
Całka Gaussa
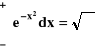
10. Def. przestrzeni probablistycznej (Ω,S,P) (S - przestrzeń zdarzeń losowych, P - funkcja prawdopodobieństwa), własności funkcji prawdopodobieństwa, prawdopodobieństwo warunkowe, niezależność zdarzeń losowych, wzór Bayes'a, schemat Bernoulliego.
Przestrzeń probablistyczna
Przestrzenią probablistyczną nazywamy trójkę: (Ω,S,P) - stanowi opis matematyczny zdarzenia losowego
Zbiór zdarzeń losowych S
(I) Niech Ω będzie zbiorem (co) najwięcej przeliczalnym (tzn. jego elementy można ustawić w ciąg).
Zbiorem zdarzeń losowych S nazywamy rodzinę wszystkich podzbiorów zbioru Ω, tzn. S = 2Ω
Uwaga:
Jeśli ![]()
to ![]()
, bo ![]()
Ω = {0,1} 2Ω = ![]()
![]()
- dwumian Newtona
![]()
(II) Niech Ω = Rn lub Ω ⊂ Rn i Ω − nieprzeliczalny. Rodzinę S* nazywamy ![]()
- algebrą (![]()
- ciałem) podzbiorów zbioru Ω, jeśli:
Ω ∈ S*
A ∈ S* ⇒ A' = Ω − A ∈ S*
A1,A2,...An ∈ S* ⇒
Funkcja prawdopodobieństwa P
Niech ∅ ≠ Ω, S - rodzina zdarzeń losowych
Rozkładem prawdopodobieństwa P na S nazywamy funkcję P: S → <0,1〉 taką, że:
P(Ω) = 1
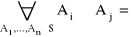
dla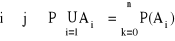
Własności prawdopodobieństwa
P(∅) = 0
A1,...,An ∈ S;
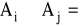
dla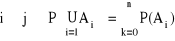
A = A1, B = A2 ![]()
- uogólnienie
P(A') = 1 - P(A)
A ⊂ B ⇒ P(B − A) = P(B) - P(A)
A ⊂ B ⇒ P(A) ≤ P(B)
P(A∪B) = P(A) + P(B) - P(A∩B)
A1 ⊂ A2 ⊂ A3 ⊂ ... ⊂ Ai ∈ S (i∈N) ⇒
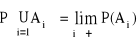
B1 ⊃ B2 ⊃ B3 ⊃ ... ⊃ Bi ∈ S (i∈N) ⇒
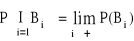
Prawdopodobieństwo warunkowe
Niech (Ω,S,P) - przestrzeń probablistyczna, B∈S, P(B)>0
Prawdopodobieństwem warunkowym zdarzenia A pod warunkiem zajścia zdarzenia B nazywamy:
![]()
Funkcję PB taką, że PB(A) = P(A/B) nazywamy warunkowym rozkładem: ![]()
![]()
![]()
, stąd:
![]()
![]()
- iloczyn prawdopodobieństw warunkowych
Niezależność zdarzeń losowych
A i B są niezależne ⇔ P(A∩B) = P(A) · P(B), P(B)>0
![]()
Zajście zdarzenia B nie wpłynęło na zajście zdarzenia A. Stąd A i B są niezależne.
A1,A2,...,An są niezależne ⇔![]()
Wzór Bayes'a
Zał. 1) ![]()
dla i ≠ j
2) ![]()
, P(Ai) > 0, P(B) > 0
Teza 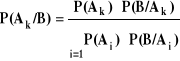
Dowód: 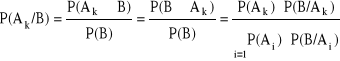
Schemat Bernoulliego
Rozważmy n - niezależnych eksperymentów (doświadczeń) losowych. Każdy z nich kończy się jednym z dwóch możliwych wyników: w1 - sukces, w2 - porażka. Zatem zbiór zdarzeń elementarnych w pojedynczym doświadczeniu: Ω = {w1;w2}. Niech p = P(w1), q = P(w2), p + q = 1.
W n - krotnym doświadczeniu zbiór zdarzeń elementarnych Ωn = Ω × ... × Ω = {(r1,...,rn); ri∈Ω; i = 1,...,n}
Niech ![]()
- zdarzenie losowe polegające na tym, że w n - krotnym doświadczeniu mamy k - sukcesów
![]()
11. Def. zmiennej losowej i jej rozkładów (skokowego i ciągłego), przykłady rozkładów skokowych (dwupunktowy, Bernoulliego, Poissona, geometryczny) i ciągłych (jednostajny, normalny, Gamma, wykładniczy, Laplace'a).
Zmienna losowa
Niech (Ω,S,P) będzie przestrzenią probablistyczną
Jeśli Ω jest zbiorem co najmniej przeliczalnym, to zmienną losową jednowymiarową nazywamy każdą funkcję X: Ω → R
Jeśli Ω jest zbiorem nieprzeliczalnym, to zmienną losową nazywamy każdą funkcję X: Ω → R spełniającą warunek
![]()
Przeciwobraz dowolnego zbioru borelowskiego A∈B(R) jest zdarzeniem losowym (należy do S)
Rozkład zmiennej losowej
Niech (Ω,S,P) będzie przestrzenią probablistyczną, a X zmienną losową określoną na Ω.
Rozkładem zmiennej losowej X nazywamy funkcję PX określoną na rodzinie zbiorów borelowskich następującym wzorem:
![]()
Trójka (R,B(R),PX) stanowi przestrzeń probablistyczną generowaną przez zmienną losową X
X - realizuje numerację zbioru zdarzeń elementarnych Ω
(Ω,S,P)![]()
(R,B(R),PX) ![]()
Rozkład skokowy zmiennej losowej
Jeśli istnieje skończony lub przeliczalny zbiór SX = {x1,x2,...} zwany zbiorem punktów skokowych taki, że ![]()
, gdzie pi = P(X = xi) ≠ 0, to mówimy, że zmienna losowa X jest typu dyskretnego lub skokowego SX = X(Ω)
Uwaga: X jest typu skokowego ![]()
Rozkład ciągły zmiennej losowej
Jeżeli istnieje nieujemna funkcja f(x) ≥ 0 zwana funkcją gęstości taka, że dla każdego x∈R dystrybuanta zmiennej losowej X jest postaci: FX(X) = ![]()
, to mówimy, że zmienna losowa X−∞ jest typu ciągłego.
P(X<x) = FX(X) = ![]()
Przykłady rozkładów zmiennej losowej
A. Rozkłady skokowe (dyskretne)
(1) Dwupunktowy (zero - jedynkowy)
X |
0 |
1 |
PX |
p |
q |
0 < p < 1, p + q = 1
Bernoulliego
Poissona
Geometryczny
Jednostajny (równomierny)
Normalny (Gaussa)
Gamma
Wykładniczy: Gamma dla p = 1
Laplace'a
jest niemalejąca
lewostronnie ciągła (tzn.
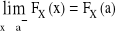
)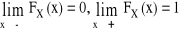
PX( [a,b] ) = FX(b) - FX(a) (Przyrost wartości dystrybuanty na przedziale [a,b] )
PX({a}) = FX(a + 0) - FX(a), gdzie FX(a + 0) =
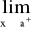
FX(a)jeśli X jest typu skokowego: SX = {x1,x2,...} oraz P(X = xi) = pi > 0, i = 1,2,... , przy czym szereg
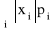
jest zbieżny, to: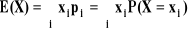
jeśli X jest zmienną losową typu ciągłego o gęstości f oraz zbieżna jest całka
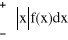
, to: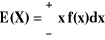
Momentem (zwykłym) rzędu k zmiennej losowej X nazywamy liczbę: mk = E(Xk)
Momentem centralnym rzędu k nazywamy liczbę μk = E[(X - m)k], gdzie m = m1 = E(X)
Wariancją nazywamy
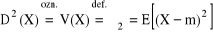
F(x0,5) = 1 - P(X ≥ x0,5) ≤ ½
X - zmienna losowa ciągła, to F(x0,5) =
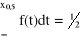
P(X = m0) =
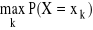
m0 - maksimum funkcji gęstości
X = (X1,...,Xn): Ω → Rn oraz
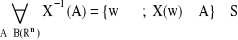
Jeśli A = A1 × ... × An i X = (X1,X2,...,Xn), to:
(X,Y) - ma rozkład ciągły o gęstości f(x,y)
Jeśli (X,Y) jest typu skokowego o rozkładzie pij = (P(X = xi, Y = yj) to rozkłady brzegowe zmiennych losowych X i Y są określone:
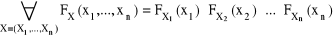
- dystrybuanta rozkładu łącznego X jest równa iloczynowi dystrybuant rozkładów brzegowychX = (X1,...,Xn) - rozkład ciągły
X = (X1,...,Xn) - rozkład skokowy
F(x,y)(x,y) = Fx(x) · Fy(y)
f(x,y)(x,y) = fx(x) · fy(y)
P(X = xi, Y = yj) = P(X = xi) · P(Y = yj)
X |
0 |
1 |
2 |
... |
k |
... |
n |
PX |
P0 |
P1 |
P2 |
... |
Pk |
... |
Pn |
PX = P(X = k) = ![]()
0 < p < 1, p + q = 1, k = 0,1,2,...,n
![]()
SX = {0,1,...}
X |
0 |
1 |
2 |
... |
k |
PX |
P0 |
P1 |
P2 |
... |
Pk |
pk = P(X = k) = ![]()
; λ > 0, k = 0,1,2,...
![]()
X |
1 |
2 |
... |
k |
PX |
P1 |
P2 |
... |
Pk |
pk = P(X = k) = pqk-1, k = 1,2,3,...
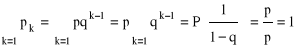
B. Rozkłady ciągłe
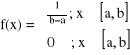
Y
![]()
f(x)
![]()
a b X
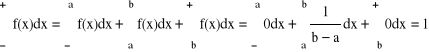
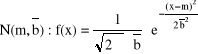
Y
![]()
f(x) KRZYWA GAUSSA
m X
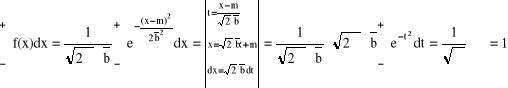
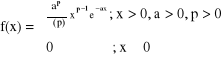
gdzie 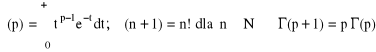
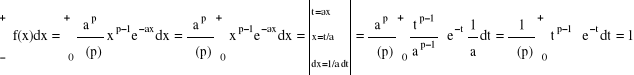
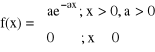
Y
a
f(x)
X
![]()
Y
![]()
X
12. Dystrybuanta zmiennej losowej, własności dystrybuanty, funkcje zmiennej losowej Y = g(X), postać funkcji zmiennej losowej fy(y).
Dystrybuanta zmiennej losowej
Dystrybuantą zmiennej losowej X nazywamy funkcję FX: R → [0,1] taką, że:
![]()
Własności dystrybuanty zmiennej losowej
Dystrybuanta FX zmiennej losowej X spełnia warunki:
Zachodzą następujące wzory:
Funkcje zmiennej losowej
Funkcję zmiennej losowej X nazywamy zmienną losową Y = g(x) taką, że
![]()
, np.:
X |
x1 |
x2 |
⇒ |
Y |
ax1+ b |
ax2+ b |
PX |
P1 |
P2 |
|
PY |
P1 |
P2 |
g: R → R
X: Ω → R Y = g(X): Ω → R Y(w) = g(X(w))
Niech Y = ax + b, fx(x) - gęstość zmiennej losowej X
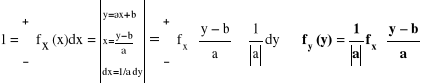
13. Parametry rozkładów zmiennej losowej (wartość oczekiwana i wariancja, mediana, moda), zmienna losowa standaryzowana.
Wartość oczekiwana zmiennej losowej
Wartością oczekiwaną zmiennej losowej X nazywamy liczbę E(X) określoną następująco:
Wariancja zmiennej losowej
Mediana zmiennej losowej
Medianą (wartością środkową) zmiennej losowej X nazywamy taką jej wartość x0,5:
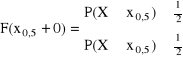
X |
−1 |
0 |
1 |
PX |
¼ |
¼ |
½ |
P(X ≥ 0) = P(X = 0) + P(X = 1) = ¼ + ½ = ¾ ≥ ½
P(X ≤ 0) = P(X = −1) + P(X = 0) = ¼ + ¼ = ½ ≥ ½
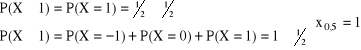
Uwaga:
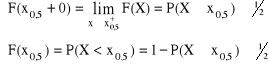
![]()
← F - ciągła ⇒ F(x0,5) = ½ ![]()
Y
x = m = x0,5 X
![]()
Moda zmiennej losowej
Modą m0 nazywamy wartość zmiennej losowej X taką, że P(X = m0) = ![]()
lub m0 - max f(x)
X |
−1 |
0 |
1 |
2 |
m0 = 0 |
PX |
1/6 |
1/3 |
1/3 |
1/6 |
m0 = 1 |
W rozkładzie normalnym moda i mediana pokrywają się
m'0 m''0
Zmienna losowa standaryzowana
Zmienną losową Y nazywamy standaryzowaną, jeśli E(Y) = 0, D2(Y) = 1
14. Zmienna losowa dwuwymiarowa (lub wielowymiarowa), dystrybuanta, rozkłady brzegowe, niezależność zmiennych losowych.
Zmienna losowa wielowymiarowa
(Ω,S,P) - przestrzeń probablistyczna
Uporządkowany układ (ciąg) n - zmiennych losowych X1,...,Xn nazywamy losową n - wymiarową i oznaczamy przez X = (X1,X2,...,Xn)
Uwaga:
![]()
Dystrybuanta zmiennej losowej wielowymiarowej
Dystrybuantą zmiennej losowej X = (X1,...,Xn) nazywamy funkcję F(X): Rn → <0,1〉 taką, że dla X = (X1,...,Xn)∈Rn
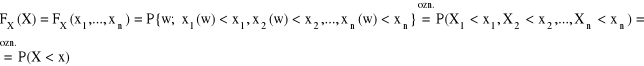
Rozkłady brzegowe
Niech X = (X1,...,Xn) - zmienna losowa n - wymiarowa
FX(X); x = (x1,...,xn) - dystrybuanta zmiennej losowej X
Dystrybuantą rozkładu brzegowego FXi(xi) zmiennej losowej xi nazywamy funkcję FXi: R → <0,1〉 taką, że:
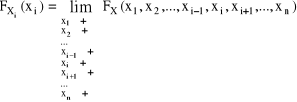
Przykład:
Dla n = 2 F(x,y) - dystrybuanta
![]()
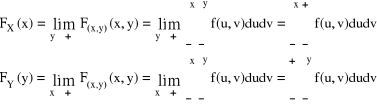
Funkcje: 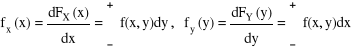
nazywamy gęstościami brzegowymi rozkładów brzegowych zmiennej losowej X i Y
![]()
Niezależność zmiennych losowych
Zmienne losowe X1,X2,...,Xn nazywamy niezależnymi, jeśli dla dowolnych zbiorów A1,...,An∈B(R) zachodzi:
![]()
Zmienne losowe są niezależne ⇔ gdy zdarzenia losowe ![]()
(dla i = 1,...,n) są niezależne
Uwaga:
![]()
- f. gęstości równa jest iloczynowi funkcji gęstości rozkładów brzegowych
![]()
Dla n = 2
15. Wartości oczekiwane funkcji Y = g(X) zmiennej wielowymiarowej X, momenty zwykłe i momenty centralne, macierz kowariancji i współczynnik korelacji.
Wartość oczekiwana
Wartością oczekiwaną funkcji g(X1,X2,...,Xn) nazywamy liczbę:
![]()
, gdy X = (X1,...,Xn) ma rozkład skokowy oraz powyższy szereg jest zbieżny bezwzględnie,
lub
![]()
, gdy X ma rozkład ciągły o gęstości f(x1,...,xn) oraz powyższa całka jest zbieżna bezwzględnie, tzn. ![]()
Dla n = 2
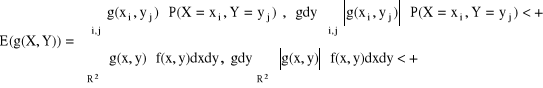
Moment zwykły
Momentem (zwyczajnym) rzędu L1 + L2 + ... +Ln nazywamy wartość oczekiwaną funkcji:
![]()
i oznaczamy: ![]()
, tzn.:
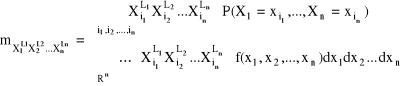
przy założeniu, że szereg i całka są zbieżne bezwzględnie
Uwaga:
Jeśli Li = 1 oraz Lj = 0 dla j ≠ i, j∈{1,...,n}, to mxi = E(Xi) - wartość oczekiwana zmiennej losowej Xi.
![]()
Uwaga (dla n = 2):
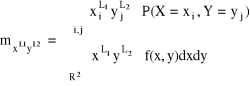
Moment centralny
Momentem centralnym rzędu L1 + L2 + ... +Ln nazywamy wartość oczekiwaną funkcji:
![]()
, gdzie ![]()
dla i = 1,2,...,n, oraz oznaczamy przez ![]()
. Zatem: ![]()
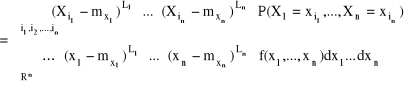
Uwaga (dla n = 2):
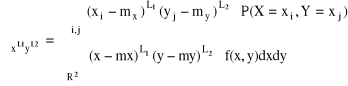
Macierz kowariancji
Kowariancją zmiennych losowych Xi oraz Xj nazywamy moment centralny rzędu 2, tzn.
![]()
Macierzą kowariancji nazywamy macierz K, gdzie ![]()
Uwaga:
![]()
- wariancja Xi. Macierz kowariancji jest symetryczną: K = KT
![]()
Współczynnik korelacji
Współczynnikiem korelacji zmiennych losowych Xi, Xj nazywamy liczbę:
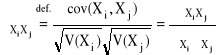
, gdzie ![]()
- odchylenie standardowe
1
![]()
Wyszukiwarka
Podobne podstrony:
Polityka podatkowa, WZ-stuff, semestr 2, nauka o przedsiębiorstwie
Materiały Kolowium Nauka o Państwie Kolos, Stosunki Międzynarodowe Rok 1, Semestr 1, Nauka o Państwi
nauka administracji, Administracja, Semestr I, Nauka administracji
Nauka o panstwie, Stosunki międzynarodowe - materiały, I semestr, Nauka o państwie (ćwiczenia)
ZŁOŻA ROZSYPISKOWE, GIG, semestr 5, Nauka o złożach
2 - Stale Konstrukcyjne Obrabiane Cieplnie, ZiIP, Semestr 2, Nauka o Materiałach z Elementami Chemii
ciaga nor, Zarządzanie ZZL studia WAT, II SEMESTR, Nauka o organizacji
Karbonatyty, GIG, semestr 5, Nauka o złożach
lab-rozciaganie, ZiIP UR Kraków, I Semestr, Nauka o materiałach
lab-Kraków-sciskanie-MTS, ZiIP UR Kraków, I Semestr, Nauka o materiałach
lab-rozciaganie, ZiIP UR Kraków, I Semestr, Nauka o materiałach
frnacja, Europeistyka, 2 semestr, Nauka o państwie, Francja prezentacja
Nauka o Państwie i prawie - wykłady, Sudia - Bezpieczeństwo Wewnętrzne, Semestr I, Nauka o Państwie
Testy(1), WZ-stuff, semestr 2, nauka o przedsiębiorstwie
Zagadnienia egzaminacyjne zima, III semestr, Nauka o polityce
nauka administracji, Administracja I rok, semestr I, Nauka administracji
Wymagania do Kolokwium nr 2 NAUKA O MATERIAŁACH, AGH WIMIIP Metalurgia, semestr 2, nauka o materiała
Rodzaje spółek, WZ-stuff, semestr 2, nauka o przedsiębiorstwie
więcej podobnych podstron