Obliczenia statyczno - wytrzymałościowe
1. Założenia ogólne
- Obiekt projektuje się dla klasy obciążeń „E”
- Użytkowa szerokość pomostu ![]()
m
0+
2. Projektowanie pokładu jezdni
Nawierzchnia asfaltobetonowa o minimalnej grubości 5-10 cm (pokład nośny podłużny) ułożona na dylinie
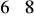
cm i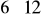
cm, układane rombem.
2.1 Obciążenie stałe
Wyszczególnienie |
Wymiar |
Wymiar |
Ciężar objętościowy |
Obciążenie charakter. |
Wsp. obc. γf |
Obciążenie obliczeniowe |
|
[ m ] |
[ m ] |
[ kN/m3] |
[ kN/m] |
|
[ kN/m] |
Asfaltobeton |
0,12 |
0,09 |
23,0 |
0,2484 |
1,5 |
0,3726 |
Dyl sosnowy |
0,12 |
0,10 |
6,0 |
0,072 |
1,2 |
0,0864 |
Suma obc.stałych |
|
|
|
0,3204 |
|
0,459 |
g0 = 0,459 kN/m
2.2 Obciążenia zmienne
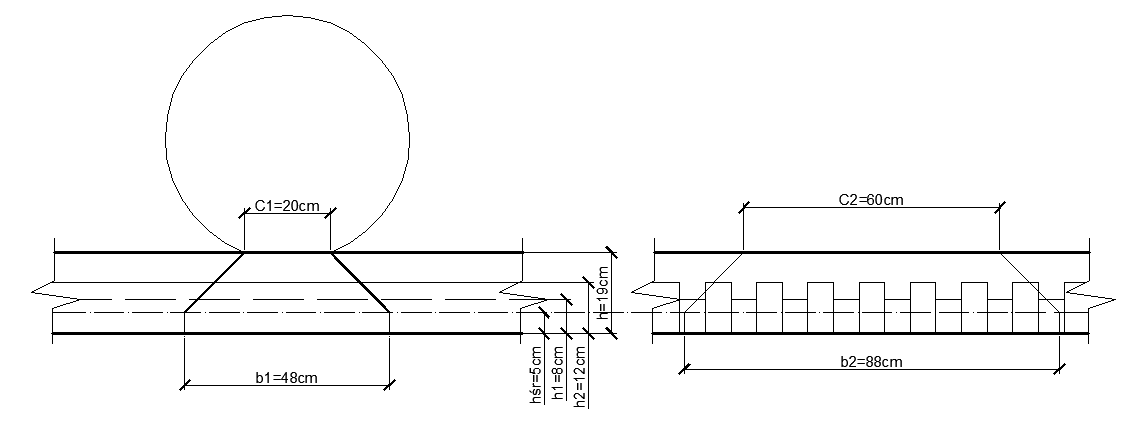
2.2.1. Rozkład obciążenia kołem
C1 = 20 cm
C2 = 60 cm
h1 = 8 cm
h2 = 12 cm
h = 19 cm
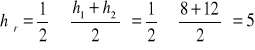
cm

- Równolegle do osi mostu - Prostopadle do osi mostu
![]()
cm
![]()
cm
2.2.2. Obciążenie taborem samochodowym „K
Wg. PN - S - 10030 , 1985r. „Obiekty mostowe. Obciążenia” dla klasy obciążenia „E”
„K”= 240 kN , nacisk na oś - 60 kN
2.2.3. Obciążenie pojazdami samochodowymi „S”
Wg. PN - S - 10030 , 1985r. „Obiekty mostowe. Obciążenia” dla klasy obciążenia „E”
„S”= 150 kN , nacisk na osie: P1 = 50 kN P2 = 100 kN a = 1,5 m
Obciążenie równomiernie rozłożone jezdni wynosi:
qj = 1,2 kN / m2
Obciążenie tłumem chodników
qt = 2,5 kN / m2
Nacisk koła taboru samochodowego „K”
Pk = ![]()
kN
Nacisk koła pojazdu samochodowego „S”
PS1 = ![]()
kN
PS2 = ![]()
kN
Do dalszych obliczeń przyjęto nacisk PS2 = 50 kN
Obciążenie równomiernie rozłożone przypadające na dwa dyle:
l = 1,0 m
l0 = 0,82 m
lt = 1,05 l0 =0,861 m
Współczynnik dynamiczny dyla
φ = 1,35 - 0,005lt < 1,325
lt = 1,05 l0 =0,861 m
φ = 1,35 - 0,005![]()
0,861 = 1,346 > 1,325 nierówność niespełniona
przyjęto φ = 1,325
Intensywność obciążenia dyla od koła pojazdu samochodowego „S”
PS2 = 50 kN b1 = 0,48 m b2 = 0,88 m γf = 1,5
- Obciążenie równomiernie rozłożone na powierzchni ![]()
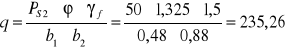
kN / m2
- Obciążenie równomiernie rozłożone przypadające na dwa dyle o szerokości 6 cm jeden
![]()
kN / m2
2.3. Obliczenie sił wewnętrznych ( M, Q )
Moment zginający w środku przęsła:
η1 = ![]()
η2 = ![]()
![]()
= 2,14 kNm
Siła tnąca na podporze:
η1 = 1 η2 = ![]()
![]()
![]()
= 9,95 kN
2.4. Sprawdzenie nośności dyla
2.4.1.Charakterystyki geometryczne przekroju:
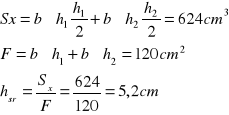
- moment bezwładności:
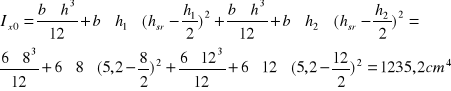
- wskaźnik wytrzymałości:
![]()
![]()
- moment statyczny brutto połowy przekroju względem osi Xo:
![]()
2.4.2. Nośność dyla na zginanie:
![]()
![]()
![]()
![]()
wg polskiej normy: PN-92/S-10082
![]()
Wytrzymałość na zginanie (włókna górne - ściskanie) wykorzystana w 91%
![]()
Wytrzymałość na zginanie(włókna dolne - rozciąganie) wykorzystana w 69%
2.4.3. Nośność dyla na ścinanie:
![]()
![]()
![]()
![]()
![]()
![]()
wg polskiej normy: PN-92/S-10082
![]()
![]()
![]()
![]()
Wytrzymałość na ścinanie wykorzystana w 92%
3.Projektowanie poprzecznicy
3.1. Obciążenia stałe na 1 m długości poprzecznicy
Wyszczególnienie:
|
Wymiar [m] |
Wymiar [m] |
Ciężar objętościowy [kN/m3] |
Obciążenie charakterystyczne [kN/m] |
Współcz. obc.
|
obciążenie obliczeniowe [kN/m] |
Asfaltobeton |
1,0 |
0,09 |
23,0 |
2,07 |
1,5 |
3,105 |
Dyl sosnowy |
1,0 |
0,10 |
6,0 |
0,6 |
1,5 |
0,9 |
Poprzecznica |
0,18 |
0,24 |
6,0 |
0,259 |
1,2 |
0311 |
Suma obc. stałych |
|
|
|
2,929 |
|
4,316 |
![]()
3.2. Obciążenia zmienne
3.2.1. Rozkład obciążenia kołem ![]()
- Równolegle do osi mostu (na długości b1)
![]()
![]()
Współczynnik dynamiczny dla poprzecznicy:
![]()
lp = 1,7 m - rozstaw osiowy dźwigarów
l0 = lp - 0,3 = 1,7 - 0,3 = 1,4 m
![]()
![]()
warunek nie spełniony
przyjęto: ![]()
Obciążenie równomiernie rozłożone na długości b1
![]()
![]()
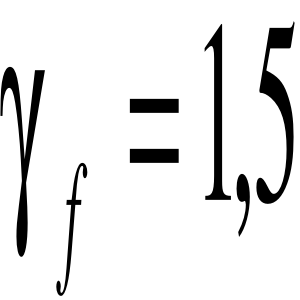
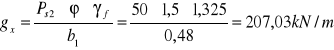
Obciążenie przypadające na poprzecznicę
![]()
- Prostopadłe do osi mostu ( na długości b2 )![]()
![]()
![]()
![]()
![]()
![]()
Obciążenie zmienne równomiernie rozłożone przypadające na jednostkę długości poprzecznicy:
![]()
3.3. Obliczenie sil wewnętrznych w poprzecznicy (M, Q):
η2 = ![]()
![]()
![]()
- Moment zginający w połowie rozpiętości:
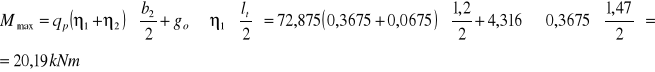
η2 = ![]()
![]()
![]()
- siła tnąca na podporze:
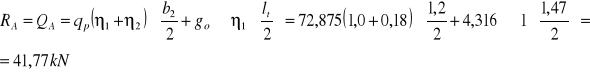
3.4. Sprawdzenie nośności poprzecznicy
3.4.1. Charakterystyki geometryczne przekroju:
- moment bezwładności
![]()
- wskaźnik wytrzymałości
![]()
- moment statyczny brutto połowy przekroju względem osi X0
![]()
3.4.2. Nośność poprzecznicy na zginanie
![]()
![]()
![]()
![]()
![]()
wg polskiej normy: PN-92/S-10082
![]()
![]()
- warunek został spełniony
Wytrzymałość na zginanie wykorzystana w 90%
3.4.3. Nośność poprzecznicy na ścinanie
![]()
![]()
![]()
![]()
![]()
![]()
![]()
wg polskiej normy: PN-92/S-10082
![]()
![]()
1,4 MPa
Wytrzymałość na ścinanie 104%
Wytrzymałość na ścinanie przekroczono o 4%
Norma PN-S-10082 dopuszcza przekroczenie stanu granicznego o 5% w szczególnych przypadkach takich jak użytkowanie mostu tymczasowego. Przekroczenie nośności o 4% mieści się w tolerancji podanej przez normę.
4. Projektowanie dźwigarów głównych.
4.1. Obciążenia stałe na 1m przęsła mostu:
Wyszczególnienie: |
|
Wymiar [m] |
Wymiar [m] |
Ciężar objętościowy [kN/m3] |
Obciążenie charakterystyczne [kN/m] |
Współczynnik odciążający γf |
Obciążenie obliczeniowe [kN/m] |
Współczynnik obciążający γf |
Obciążenie obliczeniowe [kN/m] |
I JEZDNIA: -asfaltobeton -dyl sosnowy -poprzecznica sosnowa |
1/1,0 |
1,0 1,0 0,18 |
0,09 0,10 0,24 |
23,0 6,0 6,0 |
2,3 0,48 0,259 |
0,9 0,9 0,9 |
1,86 0,54 0,233 |
1,5 1,5 1,5 |
2,79 0,81 0,3495 |
Suma stałe: |
|
|
|
|
2,929 |
|
2,633 |
gjd |
3,95 |
II CHODNIK: -pokład sosnowy -poprzecznica chod. -podłużnica chod. -poprzecznica sosnowa |
1/1,0 2/1,8 1/1,10 |
1,0 0,18 0,18 0,18 |
0,06 0,16 0,16 0,24 |
6,0 6,0 6,0 6,0 |
0,36 0,173 0,192 0,259 |
0,9 0,9 0,9 0,9 |
0,324 0,156 0,173 0,233 |
1,5 1,5 1,5 1,5 |
0,54 0,233 0,26 0,3495 |
Suma stałe: |
|
|
|
|
0,965 |
|
0,886 |
gchd |
1,38 |
III PORĘCZE: |
|
|
|
Gp |
0,5 |
0,9 |
0,45 |
1,5 |
0,75 |
IV DŹWIGAR HEB 500
|
1,3 |
|
|
Gdź |
2,431 |
0,9 |
2,1879 |
1,2 |
2,9172 |
4.2. Obciążenia zmienne na 1m przęsła mostu:
Współczynnik dynamiczny dla dźwigara:
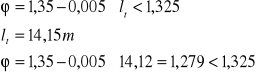
warunek spełniony
przyjęto: ![]()
Obciążenie charakterystyczne:
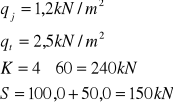
Obciążenie obliczeniowe:
-obciążenie równomiernie rozłożone w obrębie jezdni:
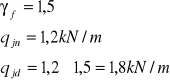
-obciążenie tłumem na chodnik:
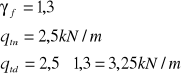
-nacisk koła taboru samochodowego „K”:
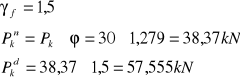
-nacisk koła pojazdu samochodowego S”:
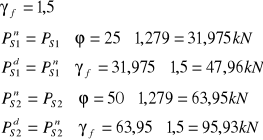
4.3. Rozdział poprzeczny obciążenia na 1,0m przęsła:
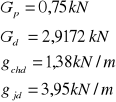
4.3.1. Dla dźwigara „A”:
![]()
![]()
![]()
![]()
η1 = 1 η2 = 1,51 η3 = 1,47 η4 = 0,412 η5 = 0,235 η6 = 0,029
-obciążenia stałe:
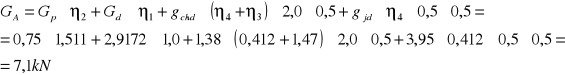
-obciążenia zmienne:
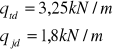
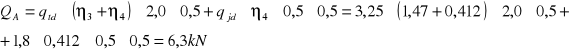
od obciążenia pojazdem samochodowym „S”:
![]()
![]()
![]()
![]()
4.3.2. Dla dźwigara „B”:
η1 = 1 η2 = 0,512 η3 = 0,471
η4 = 0,588
-obciążenia stale:
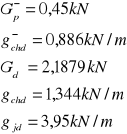
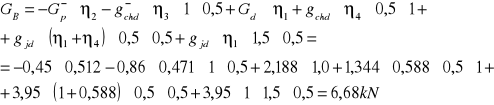
-obciążenia zmienne:
od obciążenia równomiernie rozłożonego:
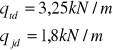
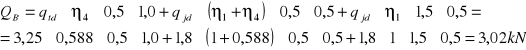
od obciążenia taborem samochodowym „K”:
![]()
![]()
od obciążenia pojazdem samochodowym „S”:
![]()
![]()
![]()
![]()
4.3.2. Dla dźwigara „C”:
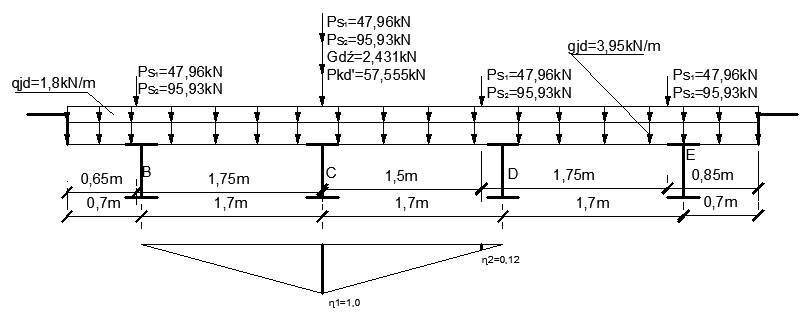
![]()
![]()
-obciążenia stałe:
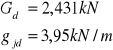
![]()
-obciążenia zmienne:
od obciążenia równomiernie rozłożonego:
![]()
![]()
od obciążenia taborem samochodowym „K”:
![]()
![]()
od obciążenia pojazdem samochodowym „S”:
![]()
![]()
![]()
![]()
4.3.4 Dla dźwigara „D”:
Rodzaj poprzecznicy i obciążenia jest identyczny jak dla dźwigara „C”
C=D; B=E; A=F.
Pomijamy obliczanie reszty dźwigarów znajdujących się w drugiej części przekroju, gdyż ich położenie jest symetryczne i siły w nich nie ulegną zmianie.
ZESTAWIENIE OBCIĄŻEŃ
Dźwigar |
G [kN] |
Q [kN] |
Obc. taborem. sam. Pkd [kN] |
Obc. p. S |
|
|
|
|
|
PS1 [kN] |
PS2 [kN] |
A |
7,1 |
6,3 |
------- |
11,27 |
22,544 |
B |
6,68 |
3,02 |
52,49 |
47,96 |
95,932 |
C |
8,356 |
2,7 |
57,555 |
53,72 |
107,44 |
D |
8,356 |
2,7 |
57,555 |
53,72 |
107,44 |
E |
6,68 |
3,02 |
52,49 |
47,96 |
95,932 |
F |
7,1 |
6,3 |
------- |
11,27 |
22,544 |
Do dalszych obliczeń przyjęto dźwigar „C
4.4. Obliczenie sił wewnętrznych w dźwigarze (M,T):
4.4.1. Obciążenie pojazdem „K”:
a.) moment zginający w połowie rozpiętości dźwigara:
![]()
![]()
![]()
![]()
η1 = 3,838 η2 = 2,338 η3 = 2,938 η4 = 2,938
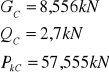
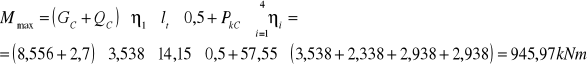
b.) siła tnąca na podporze:
η1 = 1 η2 = 0,92 η3 = 0,83 η4 = 0,75
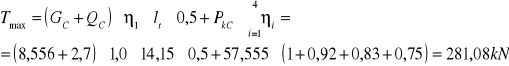
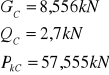
4.4.2. Obciążenie pojazdem samochodowym „S”:
a.) moment zginający w połowie rozpiętości dźwigara:
![]()
![]()
η1 = 3,538 η2 = 1,738
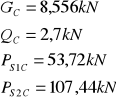
![]()
b.) siła tnąca na podporze:
η1 = 1,0 η2 = 0,75
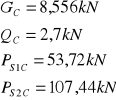
![]()
Do dalszych obliczeń przyjęto obciążenie taborem samochodowym „K”, ponieważ wywołuje znacznie większe obciążenie niż pojazd samochodowy „S”:
![]()
![]()
![]()
4.5. Sprawdzenie nośności dźwigara głównego:
4.5.1. Nośność dźwigara na zginanie:
Przyjęcie dźwigara ze stali 18G2A
Zginanie R = 280 MPa
Ścinanie Rt = 170 MPa
Wstępne wyznaczenie wymaganego wskaźnika wytrzymałości na zginanie:
![]()
Przyjęto dźwigar HEB 450, którego
Wx = 3550 cm3, Ix = 79890 cm4 Wartości odczytane z „Tablic do projektowania konstrukcji stalowych” Władysław Bogucki, Mikołaj Żuburtowicz
Sprawdzenie naprężeń:
![]()
![]()
warunek został spełniony
4.5.2. Nośność dźwigara na ścinanie:
![]()
![]()
Sprawdzenie naprężeń:
![]()
![]()
warunek został spełniony
4.5.3. Sprawdzenie ugięcia:
Maksymalna wartość momentu zginającego od obciążeń charakterystycznych:
![]()
Zgodnie z punktem 4.4.1:
![]()
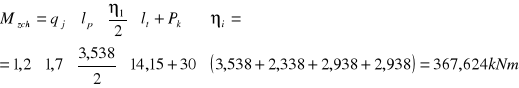
-dopuszczalna strzałka ugięcia:
![]()
-rzeczywista strzałka ugięca:
![]()
![]()
![]()
warunek został spełniony .
5. Projektowanie poręczy
5.1. Zestawienie obciążeń:
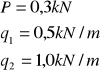
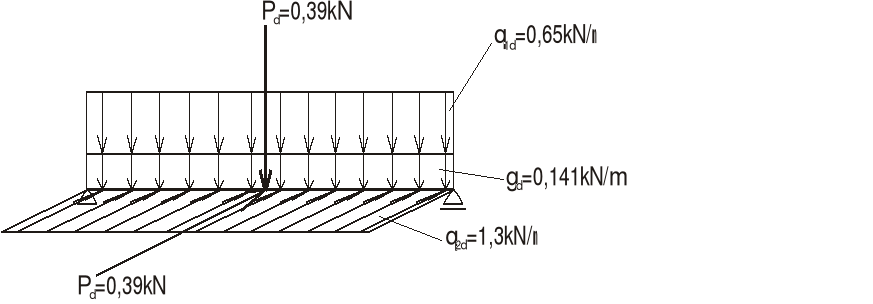
obciążenia stałe:
![]()
obciążenie zmienne:
charakterystyczne
P=0,3kN q1=0,5kN/m q2=1,0kN/m
obliczeniowe
- pionowe równomiernie rozłożone:
![]()
-poziome równomiernie rozłożone:
![]()
-skupione pionowe i poziome:
![]()
5.2 Obliczenie momentów zginających:
- od obciążenia pionowego:
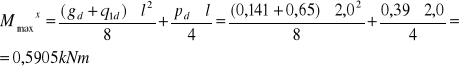
- od obciążenia poziomego:
![]()
5.3 Sprawdzenie nośności poręczy:
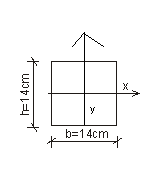
wskaźnik wytrzymałości przekroju na zginanie:
![]()
![]()
Sprawdzenie naprężeń zginających:
Mmax x=0,5905kNm Mmaxy=0,845kNm
-od obciążenia pionowego:
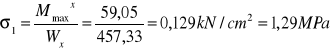
![]()
Warunek spełniony Graniczna wartość odczytana z polskiej normy:
PN-92/S-10082
- od obciążenia poziomego
![]()
![]()
Warunek spełniony
Naprężenia sumaryczne:
![]()
Warunek spełniony
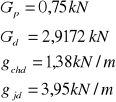
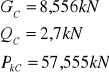
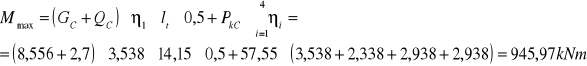
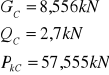
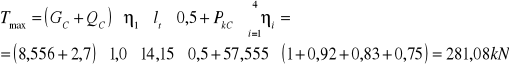
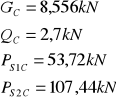
![]()
![]()
Wyszukiwarka
Podobne podstrony:
most baju, Budownictwo, Semestr V, Budownictwo komunikacyjne 1, most3
A2-3, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria kom
WYMAGANIA TECHNICZNE PODSYPKI, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Podstawy bu
OPIS DROGI, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynier
Irek, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria kom
STANDARDY KONSTRUKCYJNE NAWIERZCHN, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Podsta
wyklad Mes funkcje ksztaltu, Budownictwo, Semestr V, Budownictwo komunikacyjne 1, most5
Wykonanie kładki dla pieszych D-opis, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warsz
OGÓLNE SFORMUŁOWANIE MES DLA ZAGADNIEŃ MECHANIKI CIAŁA STAŁEGO, Budownictwo, Semestr V, Budownictwo
[14.10.2014] Kud, KONSTRUKCJE BUDOWLANE I INŻYNIERSKIE, [INŻ] SEMESTR [9], BUDOWNICTWO KOMUNIKACYJ
Anik, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria kom
Wykład 3, STUDIA budownictwo, SEMESTR V, budownictwo komunikacyjne
opis kladki, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynie
SEREK, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria ko
opis techniczny 1, Budownictwo, semestr 4, budownictwo komunikacyjne, Projekt drogowy
RADEKIK, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semestr 4, Inżynieria
IK - Projektowanie Lotnisk A, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, S
więcej podobnych podstron