15. JAKIE SĄ PRZYRZĄDY CIECZOWE DO POMIARU CIŚNIENIA.

Dla pomiaru nadciśnienia używa się manometrów, a do pomiarów podciśnienia - wakuometrów.

Najprostszym manometrem cieczowym jest otwarta u góry, cienka, przezroczysta rurka podłączona do miejsca przestrzeni cieczy, w którym należy wykonać pomiar. W rurce tej nazywanej piezometrem, znajduje się ta sama ciecz co w punkcie podłączenia. Ponieważ wylot rurki jest otwarty, więc wysokość słupa cieczy w piezometrie wyznacza wysokość nadciśnienia (h+a) w punkcie pomiaru. W celu określenia nadciśnienia gazu pn ponad zwierciadłem cieczy w zamkniętym zbiorniku wystarczy napisać równanie równowagi ciśnień dla przekroju α - α:

a stąd

Ze względu na ograniczoną długość rurek, piezometry służą do pomiaru niewielkich nadciśnień. Typowy manometr cieczowy jest wykonany z przezroczystej rurki wygiętej w kształcie litery U i wypełniony cieczą manometryczną. Gęstość cieczy manometrycznej ρcm jest większa od gęstości płynu w zbiorniku ρ. Dla określenia nadciśnienia pn ponad zwierciadłem cieczy w zbiorniku należy porównać ciśnienia, jakie panują w obu rurkach manometru w przekrojach α - przekrojach:

stąd po uproszczeniu

rysunek

Do pomiaru różnicy ciśnień Δp w dwóch zbiornikach służą manometry różnicowe . Manometr taki podłączony jest do dwóch zbiorników wypełnionych płynem o gęstości ρ. Sposób podłączenia manometru zależy od wzajemnej relacji między gęstościami ρ i ρcm Jeżeli

ρ < ρcm to manometr nazywamy U-rurkowy, jeżeli

ρ > ρcm to manometr nazywamy П-rurkowy. Wzory do obliczania różnicy ciśnień Δp wyznacza się przez porównanie ciśnień w przekrojach α - przekrojach. Wprowadzając wielkość pomocniczą x, można zapisać

-dla ρ < ρcm

a stąd po przekształceniu

-dla ρ > ρcm

rysunek

16. PARCIE CIECZY NA POWIERZCHNIE PŁASKIE ŚRODEK NAPORU.

Parcie cieczy działające na pewną powierzchnię A usytuowaną na płaskiej ścianie zbiornika, nachylonej do swobodnego zwierciadła cieczy pod kątem α. Zakłada się, że ponad swobodną powierzchnią cieczy panuje ciśnienie otoczenia p0 W przyjętym ukośnym układzie współrzędnych oś x przebiega wzdłuż krawędzi przecięcia ściany zbiornika ze zwierciadłem cieczy, oś y - prostopadle do osi x w płaszczyźnie ściany, a oś z - pionowo w dół. Parcie hydrostatyczne P, jako wypadkowa parć elementarnych prostopadłych do elementów powierzchni A, jest skierowane normalnie do tej płaszczyzny. Ciśnienie w dowolnym punkcie cieczy znajdującej się w stanie bezwzględnego spoczynku jest określone równaniem

Elementarne parcie, działające na element powierzchni dA o współrzędnych współrzędnych, współrzędnych, z wynosi

Całkowite parcie hydrostatyczne na pole A jest równe

Z zależności między współrzędnymi wynika, że

gdzie indeks s dotyczy współrzędnych środka ciężkości pola A. Całkę we wzorze można wyrazić w sposób następujący

Różniczkowe równania Eulera stosuje się zarówno dla ruchu potencjalnego, jak i wirowego. Dla ruchu wirowego można wydzielić składowe prędkości kątowej ω. Przekształcając pochodną prędkości

przy wykorzystaniu zależności

otrzymuje się

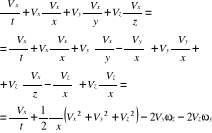
wyrażenie w nawiasie jest iloczynem skalarnym

22. PRZEDSTAWIĆ RÓWNANIE BERNOULLIEGO DLA PŁYNU DOSKONAŁEGO

Przyjmując pewne założenia, można scałkować różniczkowe równania ruchu płynu nielekkiego. Poniżej zostały podane dwa takie rozwiązania. Pierwsze rozwiązanie zostanie wyprowadzone przy założeniach:

- ruch jest ustalony,

- płyn jest barotropowy (gęstość płynu zależy tylko od ciśnienia),

- siły masowe mają potencjał, który będzie oznaczony przez - U.

Mnożąc skalarnie wszystkie składniki równania Eulera przez przesunięcia elementu po jego torze ds. = vdt, otrzymuje się

Wyrażenie po lewej stronie równania można przekształcić do postaci

Ponieważ składowe jednostkowych sił masowych wynoszą

więc rozpisując drugi iloczyn skalarny równania, otrzymuje się

Trzeci iloczyn skalarny równania można zapisać w postaci

gdzie

ostatecznie otrzymujemy

całkowanie tego równania wykonuje się wzdłuż toru

lub

U = g z

23. PRZEPŁYW UWARSTWIONY PŁYNU RZECZYWISTEGO - PROFIL PRĘDKOŚCI I RÓWNANIE HAGENA - POISEUILLE'A

Rozpatruje się ustalony przepływ płynu nieściśliwego w przewodzie kołowym o promieniu R. Tory elementów płynu są liniami prostymi, równoległymi do osi x, będącej osią przewodu. W rozważanych warunkach składowe prędkości Vy oraz Vz są równe zeru. Po pominięciu wpływu sił masowych
, trzy równania Naviera - Stokesa i równanie ciągłości uproszczą się do postaci

Sposób obliczania lewara nie różni się od obliczania przewodu krótkiego. Zakres stosowania lewara jest jednak ograniczony możliwością przerwania ciągłości przepływu wskutek wystąpienia w jego najwyższym przekroju 3 zjawiska kawitacji cieczy. W celu obliczenia prędkości średniej strumienia należy ułożyć równanie Bernoulliego dla przekrojów 1 i 2. Dla przyjętego poziomu porównawczego (p.p) równanie to przyjmuje postać

gdzie n - liczba oporów miejscowych

Dla dużych otwartych zbiorników można zapisać: p1=p2=pa oraz V1=V2=0

Po podstawieniu otrzymuje się

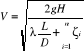
W celu obliczenia maksymalnego wzniesienia lewara H1 ponad zwierciadłem cieczy w zbiorniku zasilającym należy ułożyć równanie Bernoulliego dla przekrojów 1 i 3

gdzie m - liczba oporów miejscowych

Ciśnienie w najwyższym punkcie lewara musi być większe niż ciśnienie wrzenia cieczy pw w danej temperaturze strumienia. Podstawiając ciśnienie pw w miejsce p3, po przekształceniu otrzymuje się zależność określającą maksymalne wzniesienie lewara H1max , przy którym wrzenie cieczy nie nastąpi

35. OBLICZANIE PRZEWODÓW DŁUGICH - CHARAKTERYSTYKI.

Magistrale wodociągowe i ciepłownicze oraz rurociągi naftowe są nazywane przewodami długimi. Przewody długie charakteryzują się niewielką liczbą oporów miejscowych, a ich długość jest daleko większa niż średnica. Dla L>>D straty lokalne są małe w porównaniu ze stratami na długości i są pomijane w obliczeniach, bądź uwzględnia się je w formie mnożnika
strat liniowych. Także wysokości prędkości są pomijane w równaniu Bernoulliego, które obecnie przyjmuje postać

gdzie Hi jest naporem w i - tym przekroju strumienia

Podstawiając wydatek cieczy, stratę na długości przewodu hL można zapisać w postaci

gdzie K - przepuszczalność przewodu ( moduł przepływu)

Opornością przewodu nazywa się wyrażenie
Jego zastosowanie pozwala zapisać wysokość strat ciśnienia na długości przewodu w postaci

Przepuszczalność przewodu K zależy od średnicy przewodu oraz współczynnika λ. Jeżeli przepływ odbywa się w strefie kwadratowej zależności strat, to zanika wpływ liczby Re, a więc i wydatku Q, na wartość K

Otrzymujemy

Zależność pomiędzy wysokością strat ciśnienia ΔH a natężeniem przepływu Q jest nazywana charakterystyką przewodu. Zależności H1(Q) oraz H2(Q) wyznaczają sprawdzone charakterystyki przewodu

rysunek

36. UKŁADY PRZEWODÓW I ICH CHARAKTERYSTYKI

Połączeniem szeregowym przewodów nazywa się ciąg odcinków rur. Układ ten spełnia następujące warunki

gdzie n - liczba odcinków połączenia

gdzie hss hst - wysokość strat w przewodzie ssawnym i tłocznym

Po przekształceniu otrzymuje się

gdzie H - niwelacyjna (geometryczna) wysokość podnoszenia pompy:

Wysokością ssania pompy Hs nazywa się wysokość wzniesienia osi pompy ponad swobodne zwierciadło cieczy w zbiorniku zasilającym. Układając równanie Bernoulliego dla przekrojów 1 i s, można wyznaczyć zależność wysokości ssania Hs od parametrów przepływu w przewodzie ssawnym pompy

gdzie ps Vs - ciśnienie i prędkość w przewodzie przed pompą.

Podstawiając do powyższej zależności ciśnienie wrzenia pw otrzymuje się

Warunki pracy pompy wirnikowej określą parametry: natężenie przepływu cieczy Q, całkowita wysokość podnoszenia H0 oraz moc pompy N. Teoretyczną moc pompy N, wyrażoną w watach, W, określa się wzorem

Moc na wale pompy jest większa ze względu na opory ruchu w pompie i wynosi

gdzie ηp jest współczynnikiem sprawności pompy ( ηp=0,6-0,9)

Moc silnika pompy musi uwzględniać dodatkowo sprawność tego urządzenia (ηp=0,8-0,97)

gdzie η jest współczynnikiem sprawności instalacji pompowej

Wyrażając moc Ns w kilowatach, kW, można zapisać

40. WYPADKOWE CHARAKTERYSTYKI ZESPOŁÓW POMP W RUROCIĄGU.

Na rysunku poniżej przedstawiono zespół dwóch pomp połączonych równolegle oraz graficzny sposób wyznaczenia punktu pracy tego układu. rysunek

Połączenie równoległe jest stosowane w celu zwiększenia wydajności układu. Należy zauważyć, że łączny wydatek zespołu pomp jest równy sumie natężeń poszczególnych pomp. Natomiast każda z tych pomp dostarcza taką samą wysokość energii. W celu określenia punktu pracy należy wyznaczyć wypadkową charakterystykę zespołu pomp przez zsumowanie natężeń przepływu przy takiej samej wysokości podnoszenia. Punkt przecięcia sprowadzonej charakterystyki przewodu z wypadkową charakterystyką zespołu pompowego jest punktem pracy M.

Na rysunku poniżej przedstawiono zespół dwóch pomp połączonych szeregowo. Połączenie to pozwala zwiększyć wysokość podnoszenia układu, która jest równa sumie wysokości podnoszenia tych pomp. Wydatek zespołu odpowiada wydatkowi każdej z pomp. W celu określenia punktu pracy układu należy wyznaczyć wypadkową charakterystykę pomp, sumując rzędne wysokości podnoszenia przy tym samym natężeniu przepływu. Punkt przecięcia wypadkowej charakterystyki ze sprowadzoną charakterystyką przewodu jest punktem pracy układu M.

gdzie Sx - moment styczny pola A względem osi x. Podstawiając otrzymany rezultat do wzoru na wypadkowe parcie całkowite, otrzymuje się

Jeżeli na ściankę A od zewnętrznej strony zbiornika działa siłą wywołana ciśnieniem otoczenia p0 to wypadkowe parcie hydrostatyczne jest równe

Współrzędne środka parcia, oznaczone indeksem N, wyznacza się z prawa momentów sił. Dla określenia współrzędnej yN będącej odległością środka parcia ( punktu przyłożenia wypadkowej siły parcia) od osi x, należy przyrównać moment parcia wypadkowego do sumy momentów parć elementarnych.

czyli

Oznaczając moment bezwładności pola A względem osi x przez Jx

szukana współrzędna yN wynosi

Po uwzględnieniu zależności pomiędzy momentem bezwładności pola A względem osi x oraz osi własnej x0 ( osi równoległej do osi x, przechodzącej przez środek ciężkości pola A).

ostatecznie można zapisać

Ze wzoru wynika, że środek parcia jest położony poniżej środka ciężkości rozpatrywanej powierzchni A. W celu wyznaczenia współrzędnej xN środka parcia postępuje się podobnie, porównując momenty parcia wypadkowego i parć elementarnych względem osi y.

otrzymujemy

Oznaczając moment odśrodkowy pola A (moment dewiacji pola ) przez

szukana współrzędna xN wynosi

ponieważ

więc

współrzędna zN jest związana ze współrzędną yN zależnością

rysunek

17. PARCIE CIECZY NA POWIERZCHNIE ZAKRZYWIONE

Parcie na krzywą powierzchnię można przedstawić jako sumę geometryczną wektorów parć składowych. Obliczenie parcia sprowadza się do znalezienia składowych tej siły na kierunkach osi współrzędnych układu. Elementarne parcie wypadkowe cieczy działające na element dA zagłębiony o z pod zwierciadłem swobodnym cieczy jest równe

Składowe parcia dP w kierunku osi x i z wynoszą

maximum record size = 28 record size = 0

gdzie dAx i dAz są rzutami powierzchni dA na płaszczyznę pionową (yz) i poziomą (xy)

Składowe parcia całkowitego są równe

Równanie drugie i trzecie układu wskazują, że ciśnienie jest funkcją tylko współrzędnej x. Z czwartego równania (ciągłości) wynika, że prędkość Vx zależy wyłącznie od y i z. Z tego względu pierwsze równanie można zapisać w postaci

Ponieważ lewa strona równania jest funkcją y i z, a prawa tylko x, więc wynika stąd, że równanie może być spełnione, gdy obie strony są wielkościami stałymi

gdzie Δp oznacza różnicę ciśnień powstałą na długości L przewodu. Równanie będzie rozwiązane dla warunku brzegowego, brzegowego którym prędkość Vx przy ściance przewodu (r=R), wskutek adhezji jest równe zeru.

Łatwo można wykazać, że równanie

Stała C przyjmuje wartość

Po wykonaniu podstawień funkcja prędkości przybiera postać

Otrzymane równanie dowodzi, że dla przyjętych warunków ruchu, rozkład prędkości w przekroju poprzecznym przewodu kołowego jest paraboloidalny. Elementarny wydatek płynu dQ przez powierzchnię pierścienia dA poprzecznego przekroju przewodu kołowego jest równy

Objętościowe natężenie przepływu płynu Q w przedziale wynosi

Równanie to nosi nazwę równania Hagena - Poiseuille'a

24

Dla znanej różnicy naporów ΔH, rozwiązanie układu sprowadza się do wyznaczenia z równania strat niewiadomej Q. Zadanie to można rozwiązać graficznie. Sumując charakterystyki przewodów, przez dodanie rzędnych ΔHi przy jednakowych odciętych ( wydatkach), otrzymuje się wypadkową charakterystykę połączenia szeregowego (1+2+3). Dla zadanej wartości ΔH wyznacz się następnie szukany wydatek wydatek.

rysunek

Do połączeń szeregowych można także zaliczyć układ jak na rysunku poniżej

rysunek

rysunek tym przypadku spełnione są następujące równania:

tzn. straty całkowite są równe sumie strat, natomiast w węźle B wydatek dopływający jest równy wydatkom odpływającym. Dla danych wartości ΔH oraz QB otrzymuje się układ dwóch równań z niewiadomymi Q1 i Q2 .

Połączeniem równoległym przewodów jest nazywany układ przedstawiony na rysunku poniżej

rysunek

Układ ten jest opisany równaniami:

gdzie n - liczba przewodów połączenia równoległego (n=3)

Dla danych wymiarów geometrycznych przewodów i znanej różnicy naporów ΔH można określić przepływ Qi w przewodach połączenia równoległego, równoległego następnie wydatek dopływający/odpływający Q.

Rozwiązanie graficzne zadania jak na rysunku

Wypadkową charakterystykę połączenia równoległego (1+2+3) wyznacza się przez dodanie odciętych Qi przy stałych rzędnych (wysokościach strat ciśnienia). Pełni ona rolę charakterystyki przewodu zastępczego, który równoważy pracę całego układu. Dla znanego sumarycznego wydatku Q można obecnie wyznaczyć różnicę naporów ΔH oraz wydatki w poszczególnych przewodach.

na rysunku poniżej przedstawiono połączenie szeregowo - równoległe przewodów.

24. DOŚWIADCZENIE REYNOLDSA - OGÓLNA CHARAKTERYSTYKA PRZEPŁYWU PŁYNU LEPKIEGO.

Przepływ płynu o określonym polu prędkości i ciśnienia musi być stateczny. Przepływ jest stateczny jeśli, wytworzone w nim drobne zaburzenie z czasem wygasa. przepływ jest niestateczny, gdy zaburzenie to z czasem będzie narastać. Pierwsze badania stateczności ruchu cieczy lepkich przeprowadził Reynolds, obserwując przepływ wody przez rurkę szklaną, do której równocześnie była doprowadzona struga barwnika.

Przy małych natężeniach przepływu zabarwiona struga płynie wzdłuż osi rury, tworząc prostoliniowa smugę. przy większych prędkościach przepływu smuga ta zaczyna oscylować, tworząc linię falistą. dalsze zwiększanie prędkości wywołuje nagłe, intensywne mieszanie się obu cieczy.

Na podstawie doświadczeń Reynolds wprowadził podział przepływów na dwa zasadnicze rodzaje: przepływ laminarny (uwarstwiony) i przepływ turbulentny (burzliwy).

Przejście z ruchu laminarnego w turbulentny występuje przy pewnej wartości bezwymiarowego wyrażenia - liczby Reynoldsa.

Przejście od ruchu laminarnego do turbulentnego w przewodzie kołowym jest możliwe dla warunków, w których wartość liczby Reynoldsa zawiera się w granicach 2320<Re<50000. Wartość Re=50000 będzie nazywana górną krytyczną wartością liczby Reynoldsa Re_kr2, a Re=2320 - dolną krytyczną wartością liczby Reynoldsa (Re_kr1). Powyżej Re_kr2 nie udało się zaobserwować przepływu laminarnego. Poniżej Re_kr1 występuje tylko ruch laminarny. W praktyce inżynierskiej przyjmuje się, że dla Re>2300, przepływ jest turbulentny. Dotyczy to przeważającej liczby przypadków przepływu cieczy i gazu w przewodach. Ruch laminarny może występować w przypadku płynu o dużej lepkości poruszającego się z małą prędkością. Sprzyjają temu ruchowi przewody o małych średnicach np.: w kanalikach ośrodków porowatych.

25.PRZEDSTAWIĆ PRZEPŁYW TURBULENTNY - CECHY CHARAKTERYSTYCZNE.

Dla odpowiednio dużych wartości liczby Reynoldsa, energia przekazywana z ruchu podstawowego do pulsacyjnego jest większa niz ciepło wytworzone na skutek tarcia. W efekcie, przepływ traci stateczność, zaburzenia wzmagają się i rozprzestrzeniają, co prowadzi do nowej struktury przepływu, zwanej turbulentną. Istotą ruchu turbulentnego jest brak wewnętrznej stabilności przepływu. Występują w nim przypadkowe nieregularne zaburzenia - pulsacje (fluktuacje), które powodują, że ruch wewnątrz tego obszaru jest zmienny w czasie. Mimo, że równania Naviera - Stokesa są równaniami ogólnymi, ważnymi dla wszystkich przepływów płynów newtonowskich, ich zastosowanie do opisu ruchu turbulentnego jest udowodnione złożonością warunków początkowych i brzegowych.

można przyjąć, że prędkość przepływu turbulentnego jest sumą prędkości przeciętnej

(uśrednionej) V w pewnym przedziale czasu t₂-t₁

Oraz prędkości ruchu pulsacyjnego (fluktuacji) v'. Prędkość V wynosi więc V=v+v'. W podobny sposób można zapisać składowe prędkości oraz inne wielkości przepływu (np.: ciśnienie, gęstość). Charakter ruchu turbulentnego określają jego parametry ciśnieniowe. Składowe pulsacyjne są w czasie nieregularne. Ich prędkość v', są równe zeru.

Złożony obraz przepływu turbulentnego wskazuje na konieczność stosowania pewnych uproszczeń, w których pojęcia toru i linii prądu dotyczą pola prędkości przepływu uśrednionego. Przepływ turbulentny nazywany jest ustalonym, jeśli prędkości uśrednione v, są niezmienne w czasie. W przepływie nieustalonym pochodna lokalna prędkości uśrednionej
jest różna od zera.

Przepływ turbulentny charakteryzuje się intensywną wymianą masy oraz pędu między poszczególnymi warstwami. Występują tu naprężenia styczne τ wywołane zarówno lepkością newtonowską τ_L (naprężenie Lepkie), jak i ruchem pulsacyjnym τ_T (naprężenie turbulentne). W ruchu turbulentnym naprężenia τ_T przewyższa wielokrotnie τ_L. straty ciśnienia Δp na jednostkę długości przewodu ze wzrostem prędkości średniej Vśr narastają szybciej w przepływie turbulentnym niż w laminarnym.

27.RÓWNANIE BERNOULIEGO DLA PŁYNU LEPKIEGO - WSPÓŁCZYNNIK CORIOLISA.

Współczynnik Coiolisa (α)

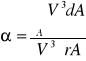
Współczynnik α jest większy od jedności. W hydraulicznych obliczeniach przyjmuje się, że dla przepływów w przewodach pod ciśnieniem α=1 (dla kanałów, oraz rzek α ≈ 1,0 do 1,2). W ruchu laminarnym w przewodzie kołowym α jest równe 2.

Równanie Bernouliego:

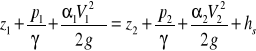
h_s - wysokość strat ciśnienia.

28. STRATY LINIOWE W RURACH HYDRAULICZNYCH GŁADKICH, WSPÓŁCZYNNIKI λ, PROMIEŃ HYDRAULICZNY.

Straty liniowe, nazywane też oporami liniowymi, oblicza się ze wzoru Darcy`ego - Weisbacha

Ostatecznie, składowe parcia wypadkowego wynoszą

Parcie wypadkowe jest sumą geometryczną parć składowych

Kierunek działania parcia P można określić zależnością

ponieważ

więc

rysunek

18. PARCIE WYRAŻONE PRZEZ FIGURY GEOMETRYCZNE - WYKRESY PARCIA

Wykresy parcia pionowego wykonuje się w następujący sposób:

- od dołu jest on ograniczony powierzchnią dla której oblicza się parcie,

- od góry wykres jest ograniczony swobodnym zwierciadłem cieczy,

- powierzchnie boczne wyznaczają linie pionowe wyprowadzone z punktów skrajnych 1 i 2 rozważanej powierzchni.

rysunek

Parcie poziome Px jest równe

Rozpatrując dowolną powierzchnię złożoną z elementów prosto- i krzywo- liniowych, przy obliczaniu parcia wypadkowego należy podzielić tę powierzchnię na części, dla których sporządza się oddzielne wykresy składowych parcia poziomego i pionowego. Przy złożeniu wykresów cząstkowych dokonuje się redukcji wykresów identycznych, lecz o przeciwnych zwrotach.

Przy obliczaniu sił parcia oraz sporządzaniu wykresów należy uwzględniać ewentualne różnice gęstości cieczy działających na różne elementy lub różne strony rozpatrywanej powierzchni.

19. WYPÓR (PRAWO ARCHIMEDESA) I RÓWNOWAGA CIAŁ ZANURZONYCH CAŁKOWICIE W CIECZY.

Na ciało całkowicie lub częściowo zanurzone w cieczy działają siły parcia hydrostatycznego oraz siła ciężkości. Rozpatrując parcie cieczy na ciało zanurzone można zauważyć, że poziome składowe parcia wzajemnie się znoszą. Dzieląc ciało pionową płaszczyzną α - α oraz stosując wzór

można stwierdzić, że skierowane przeciwnie siły Px1 i Px2 są sobie równe. W celu obliczenia parcia pionowego należy podzielić bryłę na dwie części poziomą płaszczyzną β - β. Sporządzając wykresy parcia na górną i dolną powierzchnię, po ich złożeniu można stwierdzić, że bryła wypadkowego wykresu parcia pionowego pokrywa się z bryłą ciała zanurzonego. Wypadkowa siła parcia pionowego skierowana jest ku górze i nazywa się wyporem ( siłą wyporu) W.

Jeżeli objętość zanurzonej części ciała wynosi V, a gęstość cieczy ρ, to wybór jest równy

W przypadku cieczy jednorodnej, punkt zaczepienia siły wyporu ( środek wyporu) znajduje się w geometrycznym środku zanurzonej

części ciała.

31. WYJAŚNIĆ POJĘCIA STRAT LOKALNYCH, PODAĆ PRZYKŁADY

Podczas przepływu mogą wystąpić lokalne zaburzenia wywołane zmianą kierunku ruchu, gwałtownym rozszerzeniem bądź zwężeniem, dzieleniem lub łączeniem się strumieni. Zaburzenia te rozpraszają część energii strumienia, co ujawnia się w postaci strat miejscowych.

Wysokość strat ciśnienia przy przepływie płynu przez przeszkody lokalne oblicza się ze wzoru

gdzie ζ - współczynnik oporu miejscowego.

Współczynnik ζzależy od: rodzaju przeszkody (np. zawór, kolano), parametrów geometrycznych charakteryzujących daną przeszkodę (stopień otwarcia zaworu, promień krzywizny i kąt zmiany kierunku przepływu w kolanie), a także od liczby Reynoldsa.

32. OBLICZANIE POJEDYNCZYCH PRZEWODÓW KRÓTKICH

W przewodach krótkich straty miejscowe są na tyle duże w stosunku do łącznych strat ciśnienia, że nie mogą być pominięte w obliczeniach hydraulicznych.

Obliczenia hydrauliczne pojedynczych przewodów można sprowadzić do trzech podstawowych wariantów, obejmujących wyznaczenie strat hydraulicznych hs, wydatku cieczy Q oraz doboru średnicy przewodu D. Na rysunku zaznaczono przekroje 1 i 2, dla których układa się równanie Bernoulliego. Symbolem p.p. został oznaczony poziom porównawczy, względem którego odnosi się wysokości energii w obu przekrojach. Zakłada się, że przekrój zbiornika (1) jest wielokrotnie większy od przekroju przewodu (A1 >>A2), a ruch cieczy w przewodzie jest ciągły i ustalony (Q = const)

rysunek

W celu obliczenia strat hydraulicznych hs powstałych pomiędzy przekrojami 1 i 2 należy przyjąć, że znane są wymiary przewodu ( D, L), jego chropowatość bezwzględna k, współczynniki oporów miejscowych ζ j oraz wydatek cieczy Q. Wysokość strat ciśnienia hs jest równa sumie strat liniowych hL i strat powstałych na oporach miejscowych hm . Dla przyjętego schematu straty te wynoszą

Z równania ciągłości oblicza się średnią prędkość przepływu cieczy w przewodzie

W celu określenia współczynnika oprów liniowych należy obliczyć liczbę Reynoldsa
oraz chropowatość względną

a następnie z nomogramu Colebrooka - White'a wyznaczyć współczynnik λ

Układając równanie Bernoulliego dla przekrojów 1 i 2

można obliczyć np. wskazania manometru pn2 . Dla

otrzymuje się

gdzie a- różnica wysokości między przekrojami. W celu obliczenia wydatku cieczy Q zakłada się, że znane są: wymiary geometryczne (D, L) i chropowatość k przewodu, wskazanie manometru pn2 wysokość a, jak również opory miejscowe. Z przekształcenia równania Brenoulliego otrzymujemy

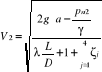
Ponieważ nie jest znana wartość Re, nie jest więc możliwe obliczenie współczynnika λ (Re, ε). W tym przypadku należy zastosować metodę kolejnych przybliżeń (iteracyjną). W pierwszym przybliżeniu zakłada się, że przepływ odbywa się w strefie kwadratowej zależności strat, λ = λ(ε) Dla odczytanej z nomogramu Colebrooka - White'a wartości λ oblicz się V2, liczbę Re i ponownie odczytuje λ. Tok obliczeń kończy się z chwilą, gdy różnica dwóch kolejnych wartości λ mieści się w zakresie przyjętej dokładności metody iteracyjnej. Ostatnia wartość prędkości V2 pozwala wyznaczyć z równania ciągłości szukany wydatek

Dla znanych wymiarów geometrycznych oraz różnicy ΔH rozwiązanie tego układu polega na określeniu wydatków Qi w przewodach tego układu. Graficzne rozwiązanie zadania, przy wykorzystaniu charakterystyk poszczególnych przewodów, pokazano na rysunku poniżej

rysunek

Wypadkowa charakterystyka połączenia równoległego (2+3) tworzy wypadkową charakterystykę całego układu (1+2+3). Dla określonej wartości ΔH można teraz odczytać wydatek Q1, a następnie przepływy Q2 oraz Q3

37. PRZEPŁYWY W UKŁADZIE TRZECH ZBIORNIKÓW.

Na rysunku poniżej pokazano zespół trzech zbiorników połączonych układem przewodów w węźle D

rysunek

Dla ułatwienia w węźle tym zmontowano piezometr. Rozwiązanie zadania polega na określeniu kierunków przepływu oraz wartości natężeń przepływu w przewodach. W przypadku gdy spełniona jest nierówność
, wówczas zbiornik A jest zawsze zbiornikiem zasilającym

a C zawsze zbiornikiem zasilanym

Zbiornik B może być:

- zasilający
, stąd dla węzła D można zapisać, że

- nieczynny

- zasilany

Zakładając że HB > HD , można wówczas ułożyć następujący układ równań

Rozwiązując ten układ, wyznacza się szukane wartości Q1 Q2 Q3 oraz HD Jeżeli obliczona wysokość HD będzie mniejsza od naporu HB, to warunki zadania będą spełnione. W przeciwnym wypadku należy przyjąć inny wariant przepływu. Na rysunku poniżej przedstawiono graficzne rozwiązanie dla trzech wariantów rozpływu cieczy w węźle D

rysunek

Wysokość tych strat jest równa stosunkowi spadku ciśnienia do ciężaru właściwego strumienia.

Wzór ten został określony dla kołowego przekroju strumienia. Dla przekrojów nie kołowych (również przy częściowym napełnieniu przewodu) straty ciśnienia oblicza się, wykorzystując pojęcie promienia hydraulicznego R_h. wielkość ta jest stosunkiem przekroju poprzecznego strumienia A do obwodu zwilżonego U.

Dla całkowicie wypełnionego cieczą przewodu kołowego wynika, że D=4R_h podstawiając ten związek do wzoru:

otrzymuje się:

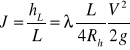
Współczynnik oporów liniowych λ w ruchu ustalonym jest w ogólnym przypadku funkcją liczby Reynoldsa i chropowatości względniej ε wewnętrznej powierzchni przewodu λ= λ(Re, ε)

Współczynnik oporów liniowych(λ) zależy tylko od Re i jest opisany wzorem Prandtla - Karmana.

w obliczeniach praktycznych stosuje się również wzór Blasiusa.

Wybór działa przeciwnie do ciężaru ciała, co powoduje pozorną utratę przez zanurzone ciało części jego ciężaru. Zjawisko to znane jest jako prawo Archimedesa.

Ciało zanurzone w cieczy znajduje się w równowadze, jeżeli jego ciężar G jest równy wyporowi W, a siły te leżą na wspólnej osi pionowej nazywanej osią pływania. Oś pływania przechodzi zarówno przez środek ciężkości ciała, jak i przez geometryczny środek jego części zanurzonej.

Dla ciał całkowicie zanurzonych w cieczy, znajdujących się w równowadze, ciężar G jest równy maksymalnej sile wyporu Wm , obliczonej dla całkowitej objętości tego ciała. Ciało tonie, gdy G > Wm . Jeżeli G < Wm , ciało jest częściowo zanurzone ( pływa ), a siłą wyporu W, równa ciężarowi G, jest odniesiona jedynie do objętości zanurzonej części ciała.

W trakcie ustalania warunków równowagi, istotnym elementem jest określenie rodzaju panującej równowagi. Rozróżnia się trzy stany równowagi: trwałą, obojętną i chwiejną.

Dla ciał całkowicie zanurzonych ( G= Wm) o rodzaju równowagi decyduje wzajemne położenie środka ciężkości ciała Sc i środka wyporu Sw.

Równowaga trwała występuje, gdy Sc znajduje się poniżej Sw. Wychylenie ciała ze stanu równowagi powoduje powstanie pary sił wymuszającej powrót do pierwotnego położenia ciała. W równowadze obojętnej środek ciężkości i wyporu pokrywają się.

Równowaga chwiejna dotyczy stanu, gdy Sc leży powyżej Sw . Wychylenie ciała o pewien kąt powoduje powstanie pary sił, która obróci ciało do pozycji odpowiadającej równowadze trwałej.

rysunek

20. STATECZNOŚĆ BRYŁ PŁYWAJĄCYCH NA POWIERZCHNI CIECZY - METACENTRUM.

W celu określenia warunków opisujących rodzaj równowagi ciał pływających rozpatrujemy ciało, które zostało wychylone z pierwotnej, pionowej pozycji. Przyjmujemy że środek ciężkości Sc leży powyżej środka wyporu Sw N skutek obrotu ciała, środek wyporu ulegnie przesunięciu do punktu S'w, zajmując położenie środka geometrycznego w warunkach wychylenia (lewa część ciała wynurzyła się, prawa zaś ulega zanurzeniu). Nowy wektor wyporu W' ( równy co do wartości pierwotnej sile W) skierowany pionowo w górę przecina oś pływania w punkcie M nazywanym metacentrum. Odległość m od środka ciężkości Sc do metacentrum M jest nazywana wysokością metacentryczną. Jeżeli Sc leży poniżej M, to wysokość metacentryczna m ma znak dodatni.

O rodzaju równowagi ciał pływających decyduje znak wysokości metacentrycznej.

Wartość wysokości metacentrycznej m, w przypadku równowagi trwałej, jest miarą stateczności obiektu pływającego. Wysokość metacentryczną wyznacza się przy założeniu, że chwilowo przyłożona zewnętrzna siła wychyla ciało o mały kąt Δφ, którego wartość wyrażona w radianach jest w przybliżeniu równa wartości sinusa i tangensa tego kąta

rysunek

21. RUCH PŁYNU NIELEPKIEGO - RÓWNANIE EULERA

Różniczkowe równanie ruchu Naviera - Stokesa dla płynu nielepkiego (υ=0) przekształca się do postaci

W rzutach na osie współrzędnych, po rozwinięciu pochodnych zupełnych składowych prędkości

otrzymuje się

układ równań nazywamy równaniami Eulera

W celu określenia średnicy przewodu D przyjmuje się, że znana jest długość przewodu L oraz, dla zadanego wydatku Q, określona jest dyspozycyjna różnica piezometrycznej linii ciśnień.

dla warunków zadania otrzymuje się

Przez porównanie ΔH z obliczonymi wartościami ΔHi przyjmuje się jako rozwiązanie zadania taką średnicę katalogową ( średnicę nominalną, lub wewnętrzną), dla której ΔHi jest równe lub nieznacznie mniejsze od dyspozycyjnej różnicy ΔH.

33. LINIE PIEZOMETRYCZNE I ENERGII

Dla zanalizowania pracy rurociągu, wskazania miejsc, gdzie może wystąpić kawitacja, określenia obciążeń warunkujących wytrzymałość konstrukcji, sporządza się wykres ciśnienia w zależności od współrzędnej liniowej mierzonej wzdłuż osi rurociągu. Na tym wykresie odkłada się zmiany ciśnienia wywołane zmianą wysokości położenia osi rurociągu i zmianą średniej prędkości, spadki ciśnienia spowodowane wszelkimi stratami i przyrosty ciśnienia wywołane pracą pomp. Wszelkie te wielkości łatwo jest obliczyć z równania Bernoulliego obejmującego straty i dostarczenie energii przez pompy. Dla przepływów cieczy stosujemy często określanie ciśnienia w jednostkach wysokości słupa cieczy przepływającej rurociągiem, wtedy rzędne na wykresie mają wymiar liniowy. Rzędne te odpowiadają wysokościom słupów cieczy w otwartych rurkach pionowych, które możemy przyłączyć do przewodu we wszystkich interesujących punktach. Takie rurki do pomiaru ciśnienia ( nadciśnienia ) nazywa się piezometriami. Stąd też wykres ciśnień wyrażony w jednostkach wysokości słupa cieczy, której przepływ badamy, nazywamy wykresem piezometrycznym ( linią piezometryczną). Jeżeli w przewodzie występują podciśnienia, rurki piezometryczne należałoby zastąpić rurkami w kształcie litery U. Jeżeli wzdłuż wyprostowanej osi rurociągu wykonamy wykres jednostkowego strumienia energii ( mechanicznej), wykres taki nazwiemy w skrócie „ wykresem energii” ( linią energii). Na wykresie tym odkłada się tylko straty energii oraz jej przyrost ( pompa).

Na wykresie piezometrycznym mogą występować wzrosty ciśnienia wywołane powiększeniem przekroju lub obniżeniem osi przewodu.

Na rysunku przedstawiono wykres piezometryczny i wykres energii mechanicznej wybranego przewodu. Jeżeli sporządzimy wykres energii mechanicznej idąc od obydwu końców przewodu aż do pompy, to odcinek zamykający określi niezbędną moc pompy, tj. energię, jaką pompa musi dostarczyć cieczy w jednostce czasu.

34. PRZEPŁYW CIECZY PRZEZ LEWAR

Lewarem nazywa się przewód umożliwiający przepływ cieczy między zbiornikami, którego oś wznosi się powyżej swobodnego zwierciadła w zbiorniku zasilającym. Warunkiem powstania ruchu w lewarze jest jego wstępne napełnienie cieczą. Wylot z lewaru może być swobodny lub zanurzony w zbiorniku dolnym ( odbiorniku).

rysunek

38. OBLICZANIE SIECI PRZEWODÓW - ROZGAŁĘZIONEJ I PIERŚCIENIOWEJ.

Sieć rozgałęzieniowa

Obliczanie otwartej sieci przewodów nie jest trudne. Można zauważyć, że dla zadanych wydatków węzłowych dopływających lub odpływających na zewnątrz sieci, określone SA przepływy Qi we wszystkich gałęziach układu. Obliczenia hydrauliczne sprowadzają się do doboru np. średnic przewodów oraz wyznaczenia strat ciśnienia w odcinkach sieci.

Średnice przewodów Di można dobierać dla średniego spadku hydraulicznego Isr w danym ciągu przewodów. W tym celu należy:

- wytypować główny ciąg sieci ( przwód magistralny) od punktu zasilania A do najdalej położonego punktu E,

- obliczyć długość tego ciągu
oraz różnicę naporów między punktami skrajnymi ΔHAE

- obliczyć średni spadek hydrauliczny ciągu

gdzie n - liczba gałęzi danego ciągu (n=4)

otrzymuje się

Obliczone współczynniki przepuszczalności

( moduły przepływu) Ki pozwalają dla danej chropowatości k dobrać z tablic lub obliczyć średnice przewodów Di ciągu magistralnego. Po zaprojektowaniu (dobraniu średnic) tego ciągu przewodów należy obliczyć wysokość strat ciśnienia i sprawdzić, czy nie przekracza ona zadanej różnicy naporów ΔHAE W przypadku przekroczenia należy przyjąć odpowiednio większe średnice dla niektórych odcinków i ponownie wykonać obliczenia sprawdzające.

Sieć pierścieniowa

Obliczenie wydatków cieczy w gałęziach sieci pierścieniowej jest oparte na następujących warunkach:

- algebraiczna suma wydatków wydatków węźle jest równa zeru

gdzie m - liczba wydatków wydatków węźle (m=3)

Przy sumowaniu można przyjąć dopływy ze znakiem plu, a odpływy ze znakiem minus

- algebraiczna suma strat ciśnienia w każdym pierścieniu jest równa zeru

gdzie n - liczba gałęzi ( przewodów) w pierścieniu (n=4)

Podczas sumowania przyjmuje się straty ciśnienia za dodatnie, gdy przepływ jest zgodny z ruchem wskazówki zegara.

Dla sieci o w węzłach i p pierścieniach można ułożyć w sposób nietożsamościowy w - 1 równań bilansu cieczy w węzłach. ponadto dla każdego pierścienia jest spełnione równanie strat ciśnienia. Łącznie więc otrzymuje się p + w - 1 równań. Z zależności geometrycznych wynika, że suma wszystkich gałęzi sieci r jest równa p + w - 1. Oznacza to, że liczba szukanych wydatków wydatków przewodach odpowiada liczbie równań dyspozycyjnych. Istotnym elementem rozwiązania jest właściwe ustalenie kierunku przepływu cieczy we wszystkich przewodach. W przypadku niewłaściwego przyjęcia tych kierunków obliczone wydatki nie będą spełniać warunków fizycznych układu ( np. tylko wydatki ujemne). Rozwiązanie układu równań opisujących sieć pierścieniową, dla właściwie przyjętych kierunków przepływu, składa się z dwóch wartości, z których tylko jedna spełnia warunki zadania.

39. POJEDYŃCZA POMPA W RUROCIĄGU.

Pompa jest urządzeniem, które pobierając energię z zewnątrz przekazuje ją strumieniowi cieczy. Instalacja pompowa składa się z przewodu ssawnego, zespołu pompowego i przewodu tłocznego jak na rysunku poniżej

rysunek

Wysokość energii, jaką ma dostarczać pompa przepływającej cieczy, jest nazywana całkowitą wysokością podnoszenia pompy - H0. Wielkość H0 określa się z równania Bernoulliego dla dwóch przekrojów 1 i 2, założonych po obu stronach pompy

15. JAKIE SĄ PRZYRZĄDY CIECZOWE DO POMIARU CIŚNIENIA

16. PARCIE CIECZY NA POWIERZCHNIE PŁASKIE ŚRODEK NAPORU.

17. PARCIE CIECZY NA POWIERZCHNIE ZAKRZYWIONE

20. STATECZNOŚĆ BRYŁ PŁYWAJĄCYCH NA POWIERZCHNI CIECZY - METACENTRUM.

22. PRZEDSTAWIĆ RÓWNANIE BERNOULLIEGO DLA PŁYNU DOSKONAŁEGO

23. PRZEPŁYW UWARSTWIONY PŁYNU RZECZYWISTEGO - PROFIL PRĘDKOŚCI I RÓWNANIE HAGENA - POISEUILLE'A

35. OBLICZANIE PRZEWODÓW DŁUGICH - CHARAKTERYSTYKI.

27.RÓWNANIE BERNOULIEGO DLA PŁYNU LEPKIEGO - WSPÓŁCZYNNIK CORIOLISA.

28 PRZEDSTAWIĆ . STRATY LINIOWE W RURACH HYDRAULICZNYCH GŁADKICH, WSPÓŁCZYNNIKI λ, PROMIEŃ HYDRAULICZNY.

29.PRZEPŁYW TURBULENTNY - CECHY CHARAKTERYSTYCZNE33. LINIE PIEZOMETRYCZNE I ENERGII

34. PRZEPŁYW CIECZY PRZEZ LEWAR

39. POJEDYŃCZA POMPA W RUROCIĄGU.

32. OBLICZANIE POJEDYNCZYCH PRZEWODÓW KRÓTKICH

31. WYJAŚNIĆ POJĘCIA STRAT LOKALNYCH, PODAĆ PRZYKŁADY

19. WYPÓR (PRAWO ARCHIMEDESA) I RÓWNOWAGA CIAŁ ZANURZONYCH CAŁKOWICIE W CIECZY.

18. PARCIE WYRAŻONE PRZEZ FIGURY GEOMETRYCZNE - WYKRESY PARCIA

40. WYPADKOWE CHARAKTERYSTYKI ZESPOŁÓW POMP W RUROCIĄGU.

36. UKŁADY PRZEWODÓW I ICH CHARAKTERYSTYKI

17. PARCIE CIECZY NA POWIERZCHNIE ZAKRZYWIONE

37. PRZEPŁYWY W UKŁADZIE TRZECH ZBIORNIKÓW.

20. STATECZNOŚĆ BRYŁ PŁYWAJĄCYCH NA POWIERZCHNI CIECZY - METACENTRUM.

24. DOŚWIADCZENIE REYNOLDSA - OGÓLNA CHARAKTERYSTYKA PRZEPŁYWU PŁYNU LEPKIEGO.

38. OBLICZANIE SIECI PRZEWODÓW - ROZGAŁĘZIONEJ I PIERŚCIENIOWEJ.

21. RUCH PŁYNU NIELEPKIEGO - RÓWNANIE EULERA

---