1.Kinematyka punktu materialnego(prędkość przyspieszenie)
punktem materialnym nazywamy ciało obdarzone masą lecz nie mające objętości a więc takie które nie może obracać się ani wykonywać drgań własnych
Prędkość Prędkość jest zmianą odległości w jednostce czasu.
Prędkość stała Jeżeli ciało, które w pewnej chwili t0 znajdowało się w położeniu x0, porusza się ze stałą prędkością v to po czasie t znajdzie się w położeniu x danym związkiem x-x0 = v(t − t0) czyli
![]()
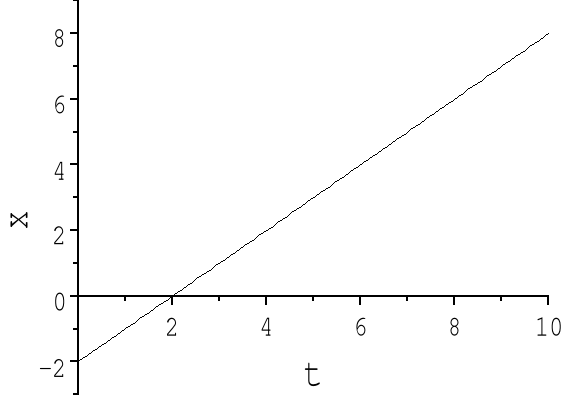
Interpretacja graficzna: prędkość to nachylenie prostej x(t) (różne nachylenia wykresów x(t) odpowiadają różnym prędkościom).
Wielkość v (wektor) może być dodatnia albo ujemna, jej znak wskazuje kierunek ruchu !!! Wektor v ujemny to ruch w kierunku malejących x.
2.Prędkość chwilowa
Jeżeli obiekt przyspiesza lub zwalnia to wskazania szybkościomierza nie zgadzają się z wyrażeniem (2.1) chyba, że weźmiemy bardzo małe wartości x − x0 (Δx) czyli również bardzo małe t - t0 (Δt). Stąd prędkość chwilowa: ![]()
Tak definiuje się pierwszą pochodną, więc ![]()
Prezentacja graficzna
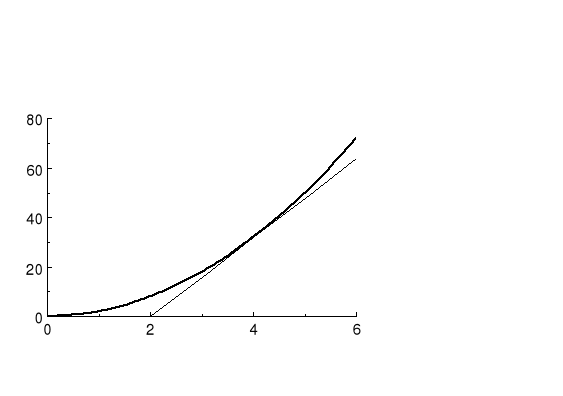
Prędkość chwilowa przejście od siecznej do stycznej. Nachylenie stycznej to prędkość chwilowa (w chwili t odpowiadającej punktowi styczności).
Prędkość średnia
Średnia matematyczna. Znaczenie średniej - przykłady. Przykłady rozkładów niejednostajnych - czynniki wagowe.
Przykład 1
Samochód przejeżdża odcinek 20 km z prędkością 40 km/h a potem, przez następne 20 km, jedzie z prędkością 80 km/h. Oblicz prędkość średnią.
t1 = x1/v1 = 20/40 = 0.5 h
t2 = x2/v2 = 20/80 = 0.25 h
![]()
= 53.33 km/h
a nie 60 km/h; (wagi statystyczne). Ponieważ viti = xi więc ![]()
przesunięcie wypadkowe/czas całkowity.
Przykład 2
Korzystamy z wartości średniej do obliczenia drogi hamowania samochodu, który jedzie z prędkością 25 m/s (90 km/h). Czas hamowania 5 sekund. Prędkość maleje jednostajnie (stała siła hamowania). Prędkość średnia 12.5 m/s (45 km/h).
Z równania (2.3) x - x0 = 12.5·5 = 62.5 m.
To najkrótsza droga hamowania. Wartość średnia daje praktyczne wyniki. Ten przykład wprowadza nas do omówienia przyspieszenia
3.Ruch jednowymiarowy
4. Przyspieszenie
Przyspieszenie to tempo zmian prędkości.
Przyspieszenie jednostajne i chwilowe
Prędkość zmienia się jednostajnie z czasem czyli przyspieszenie ![]()
jest stałe.Gdy przyspieszenie zmienia się z czasem musimy wtedy ograniczyć się do pomiaru zmian prędkości Δv w bardzo krótkim czasie Δt (analogicznie do prędkości chwilowej). Odpowiada to pierwszej pochodnej v względem t. ![]()
Ruch jednostajnie zmienny
![]()
Ponieważ w ruchu jednostajnie przyspieszonym prędkość rośnie jednostajnie od v0 do v więc prędkość średnia wynosi ![]()
= (v0 + v)/2
Łącząc otrzymujemy x = x0 + (1/2) (v0 + v)t
gdzie za v możemy podstawić v0 + at. Wtedy
x = x0 + (1/2) [v0 + (v0 +at)] t
więc ostatecznie ![]()
Dyskutując ruch po linii prostej możemy operować liczbami, a nie wektorami bo mamy do czynienia z wektorami równoległymi. Jednak trzeba sobie przy opisie zjawisk (rozwiązywaniu zadań) uświadamiać, że mamy do czynienia z wektorami.
5. Spadek swobodny.
Gdy nie występuje opór powietrza wszystkie ciała niezależnie od ich rozmiarów ciężaru i składy chemicznego w tym samym punkcie nad powierzchnią ziemi spadają z takim samym przyspieszeniem. Ponadto, jeżeli odległość przebywania przez te ciała nie jest duża to przyspieszenie nie zmieni swojej wartości. Taki idealny ruch, w którym zaniedbujemy opór powietrza oraz zmiany przyspieszenia z wysokością nazywamy spadkiem swobodnym
Np. jeżeli z takiej samej wysokości zrzucimy piłkę i zmiętą kartkę papieru to zauważymy że spadną one w tym samym czasie na ziemię w równaniach tych należy zastąpić x przez y i przyjąć że y0=0
vy=vy0+ayt
y=0,5(vy0+vy)t
y=vy0t+0,5ayt2
Vy2=vy20+2ayy
g jest wektorem pionowo skierowanym w dół a więc w kierunku ujemnym osi y.
6.. Ruch punktu materialnego na płaszczyźnie
Ruch na płaszczyźnie
Ruch w dwóch wymiarach będziemy opisywać w układzie współrzędnych x i y. Np. y - wysokość, x - odległość w kierunku poziomym. Pokażemy, że taki ruch można traktować jak dwa niezależne ruchy jednowymiarowe.
Przemieszczenie, prędkość i przyspieszenie.
Położenie punktu w chwili t przedstawia wektor r; prędkość wektor v; przyspieszenie wektor a. Wektory r, v, a są wzajemnie zależne od siebie i dadzą się przedstawić (za pomocą wersorów i, j, k czyli wektorów jednostkowych) w postaci
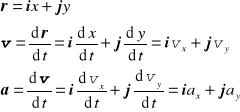
Czy trzeba stosować rozkładanie wektorów na składowe?
Przykład 1
Żaglówka płynąca pod wiatr (pod kątem 45° do kierunku wiatru). Siła, którą wiatr działa na żagiel, popycha łódkę prostopadle do płaszczyzny żagla. Ze względu na kil (i ster) łódź może poruszać się wzdłuż osi kila. Składowa siły w tym kierunku (Fx) ma zwrot w kierunku ruchu.
Ruch ze stałym przyspieszeniem oznacza, że nie zmienia się kierunek ani wartość przyspieszenia tzn. nie zmieniają się również składowe przyspieszenia.
Rozpatrzymy teraz przypadek punkt materialnego poruszającego się wzdłuż krzywej leżącej na płaszczyźnie. Rozpoczniemy od napisania równań dla ruchu jednostajnie przyspieszonego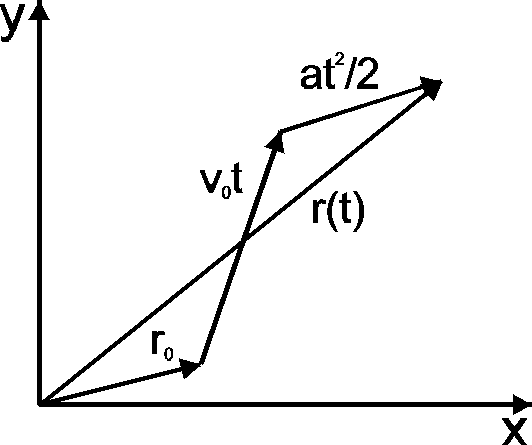
a = const, v = v0 + at, r = r0 + v0t + (1/2) at2
Prześledźmy teraz dodawanie wektorów na wykresie. Przykładowo punkt porusza się z przyspieszeniem a = [2,1], prędkość początkowa v0 = [1,2], a położenie początkowe, r0 = [1,1]. Szukamy położenia ciała np. po t = 1s i t = 3s dodając odpowiednie wektory tak jak na rysunku obok.
Powyższe równania wektorowe są równoważne równaniom w postaci skalarnej:
Równania opisujące ruch wzdłuż osi x |
Równania opisujące ruch wzdłuż osi y |
ax = const vx = vx0t + axt x = x0 + vx0t + (1/2) axt2 |
ay = const vy = vy0t + ayt y = y0 + vy0t + (1/2) ayt2 |
Przykładem na którym prześledzimy ruch krzywoliniowy ze stałym przyspieszeniem jest rzut ukośny.
7. Rzut ukośny
Rzut ukośny to ruch ze stałym przyspieszeniem g [0, -g] skierowanym w dół. Jest opisywany przez równania podane powyżej w tabeli. Przyjmijmy, że początek układu współrzędnych pokrywa się z punktem, z którego wylatuje ciało tzn. r0 = 0.
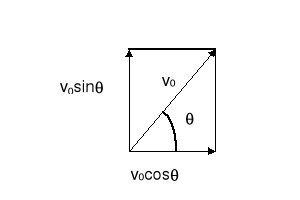
Prędkość w chwili początkowej t = 0 jest równa v0 i tworzy z kąt θ z dodatnim kierunkiem osi x. Zadaniem naszym jest: znaleźć prędkość i położenie ciała w dowolnej chwili, opisać tor, znaleźć zasięg. Składowe prędkości początkowej (zgodnie z rysunkiem) wynoszą odpowiednio vx0 = v0 cosθ i vy0 = v0 sinθ
Prędkość w kierunku x (poziomym) vx = vx0 + axt ponieważ ax = 0 więc: vx = v0 cosθ, czyli w kierunku x ruch jest jednostajny (składowa x prędkości jest stała)
W kierunku y (pionowym) vy = vy0 + ayt ponieważ gy = -g więc vy = v0 sinθ - gt
Wartość wektora wypadkowego prędkości w dowolnej chwili wynosi
![]()
więc![]()
Teraz obliczamy położenie ciała x = v0xt
czyli x = v0 cosθ t
y = v0yt+(1/2)ayt2
czyli y = v0 sinθ t - (1/2)gt2
Długość wektora położenia r można teraz obliczyć dla dowolnej chwili t z zależności ![]()
Sprawdźmy po jakim torze porusza się nasz obiekt tzn. znajdźmy równanie krzywej y(x). Mamy równania x(t) i y(t). Równanie y(x) obliczymy eliminując t z równań
t = x/v0 cosθ więc równanie przyjmuje postać ![]()
Otrzymaliśmy równanie paraboli (ramionami w dół).
Z równania paraboli obliczamy zasięg Z czyli znajdziemy miejsca zerowe. Do równaniawstawiamy x = Z oraz y = 0 i otrzymujemy po przekształceniach dwa miejsca zerowe Z = 0
Oraz ![]()
Z równania wynika, że zasięg jest maksymalny gdy θ = 45°. Zauważmy, że omawiany ruch odbywa się po linii krzywej. W poprzednich wykładach mówiliśmy o przyspieszeniu zmieniającym wartość prędkości, a nie jej kierunek (zwrot). Mówiliśmy o przyspieszeniu stycznym.
Rozpatrzmy teraz sytuacje gdy wartość prędkości się nie zmienia a zmienia się kierunek.
8. Ruch jednostajny po okręgu
Rozważmy zamieszczony obok rysunek. Punkt P - położenie punktu materialnego w chwili t, a P' - położenie w chwili t + Δt. Wektory v, v' mają jednakowe długości ale różnią się kierunkiem; są styczne do toru (krzywej) odpowiednio w punktach P i P'.
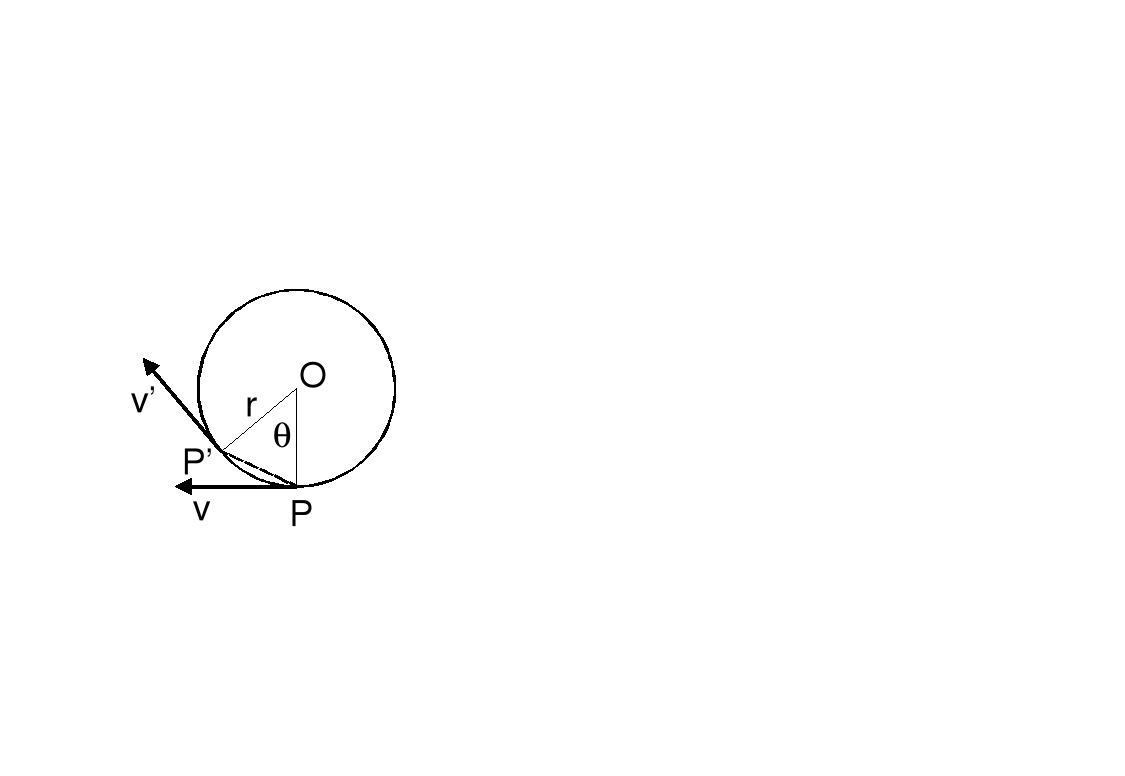
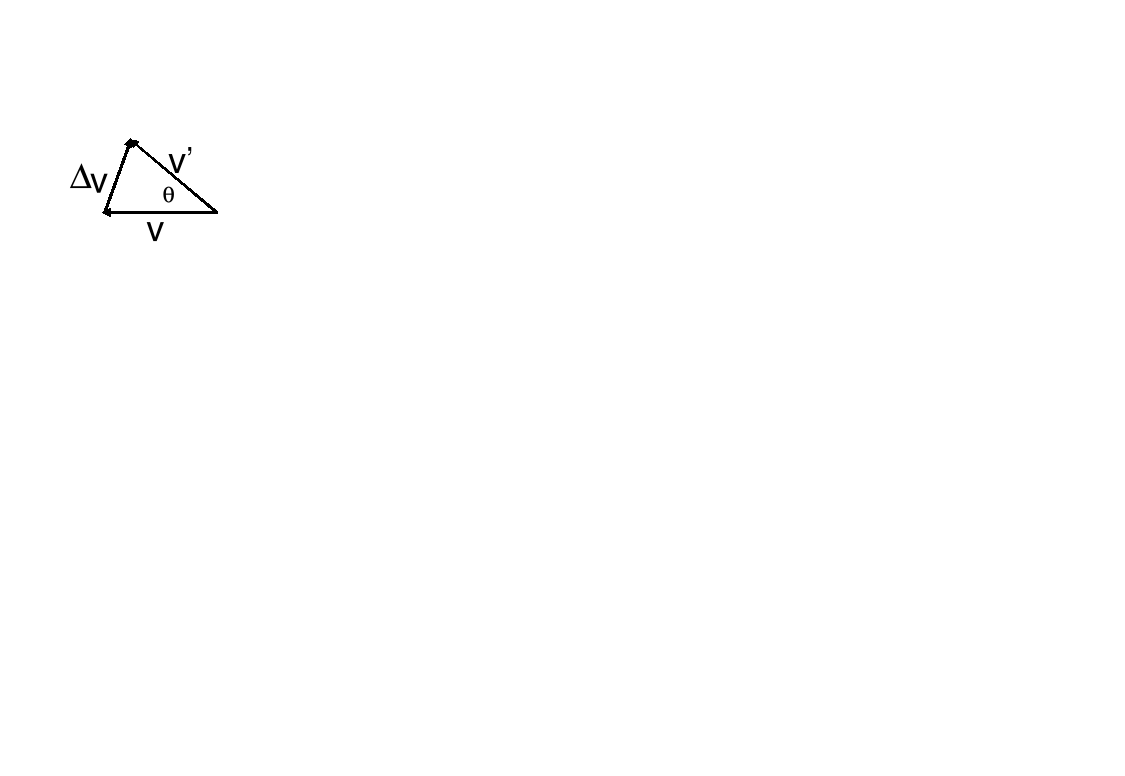
Przerysujmy wektory v i v' zaznaczając zmianę prędkości Δv. Zauważmy, że kąt pomiędzy tymi wektorami jest taki sam jak kąt na pierwszym rysunku. Zaznaczone trójkąty są podobne więc :![]()
, gdzie l jest długością łuku (pod warunkiem, że l jest bardzo małe (l→0)). Stąd
Δv = vl/r.
a ponieważ l = v Δt więc Δv = v2 Δt/r Ostatecznie a = Δv/Δt więc ![]()
To przyspieszenie nazywamy przyspieszeniem normalnym (w odróżnieniu od stycznego) bo jest prostopadłe do toru. W przypadku ruchu po okręgu kierunek prostopadły do toru jest skierowany do środka i dlatego takie przyspieszenie nazywamy również przyspieszeniem dośrodkowym. Przyspieszenie normalne zmienia kierunek prędkości.
Często wyraża się to przyspieszenie przez okres T. Ponieważ v = 2πr/T więc a = 4π2r/T2
Przykład 2
Jakiego przyspieszenia dośrodkowego, wynikającego z obrotu Ziemi, doznaje ciało będące na równiku? RZ = 6370 103 m, T = 8.64 104 sec.
a = 0.0034 m/s2. Stanowi to 0.35 % przyspieszenia ziemskiego g = 9.81 m/s2.
Przy założeniu, że Ziemia jest kulą waga na równiku jest mniejsza (np. łatwiej pobić rekord w skoku wzwyż).
Prześledźmy teraz przykład, w którym zmienia się i wartość i kierunek prędkości. Wracamy do rzutu ukośnego. Przyspieszenie g (jedyne) jest odpowiedzialne za zmianę zarówno wartości prędkości jak i jej kierunku.
Prezentacja graficzna z zaznaczeniem przyspieszenia stycznego i normalnego (jako składowych g) jest przedstawiona poniżej.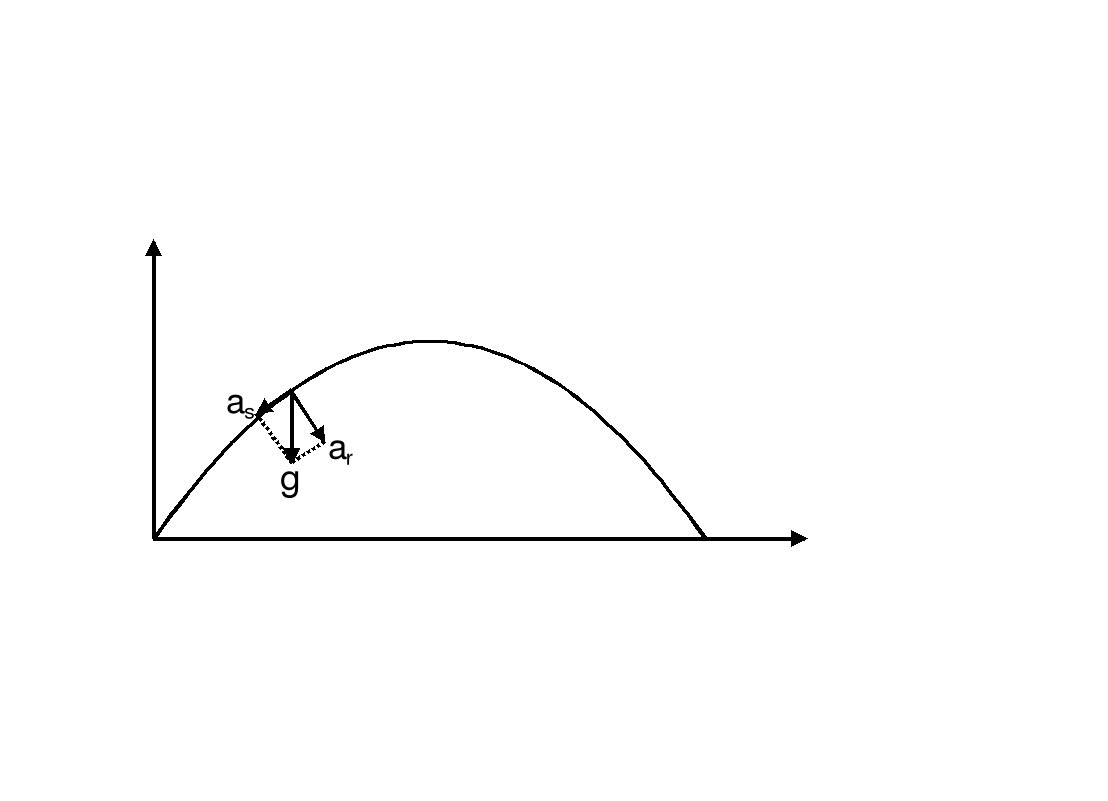
Teraz obliczymy obie składowe przyspieszenia.
Przyspieszenie styczne
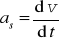
Przypomnijmy, że zależność v(t) w rzucie ukośnym jest dana równaniem (
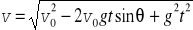
).
Stąd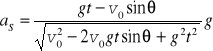
b) Przyspieszenie dośrodkowe
Jak wynika z rysunku ![]()
lub ![]()
ale trzeba umieć obliczyć promień krzywizny w każdym punkcie toru.
9. Pojęcie siły
Siła Jeżeli na ciało o masie m działa pojedyncza siła F1, to definiujemy ją jako zmianę w czasie pędu ciała.![]()
(4.3a) po rozwinięciu![]()
Dla ciała o stałej masie![]()
(4.3b) Przykłady układów o stałej i zmiennej masie.
10. Zasady dynamiki Newtona.
Sformułowanie pierwszej zasady dynamiki Newtona
Ciało pozostaje w stanie spoczynku lub w stanie stałej prędkości (zerowe przyspieszenie) gdy jest pozostawione samo sobie (działająca na nie siła wypadkowa jest równa zero).
a = 0, gdy Fwypadkowa = 0
gdzie Fwypadkowa jest sumą wektorową wszystkich sił działających na ciało.
Uwaga: a = 0, oznacza, że nie zmienia się ani wartość ani kierunek tzn. ciało jest w spoczynku lub porusza się ze stałą co do wartości prędkością po linii prostej (stały kierunek).
Sformułowanie drugiej zasady dynamiki Newtona
Tempo zmiany pędu ciała jest równe sile wypadkowej działającej na to ciało. ![]()
(4.4)
Zwróćmy uwagę, że w definicji F mówimy o pojedynczej sile, a tu mamy do czynienia z siłą wypadkową.
Sformułowanie trzeciej zasady dynamiki Newtona
Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na drugie
FA→B = - FB→A
Pierwsza zasada dynamiki Newtona
Pierwsza zasada wydaje się być szczególnym przypadkiem drugiej. Przypisujemy jej jednak wielką wagę ze względów historycznych (przełamanie dogmatu Arystotelowskiego, że wszystkie ciała muszą się zatrzymać gdy nie ma sił zewnętrznych) oraz dlatego, że zawiera ważne prawidło fizyczne: istnienie inercjalnego układu odniesienia.
Pierwsza zasada dynamiki stwierdza, że jeżeli na ciało nie działają siły zewnętrzne to istnieje taki układ odniesienia, w którym to ciało spoczywa lub porusza się ruchem jednostajnym prostoliniowym. Taki układ nazywamy układem inercjalnym.
Każdy ruch musi być opisany względem pewnego układu odniesienia. Układy inercjalne są tak istotne bo we wszystkich takich układach ruchami ciał rządzą dokładnie te sama prawa. Większość omawianych zagadnień będziemy rozwiązywać właśnie w inercjalnych układach odniesienia. Zazwyczaj przyjmuje się, że są to układy, które spoczywają względem gwiazd stałych ale układ odniesienia związany z Ziemią w większości zagadnień jest dobrym przybliżeniem układu inercjalnego.
Ponieważ przyspieszenie ciała zależy od przyspieszenia układu odniesienia (obserwatora), w którym jest mierzone więc druga zasada dynamiki jest słuszna tylko, gdy obserwator znajduje się w układzie inercjalnym. Inaczej mówiąc, prawa strona równania F = ma zmieniałaby się w zależności od przyspieszenia obserwatora.
Zauważmy, że pierwsza zasada nie wprowadza żadnego rozróżnienia między ciałami spoczywającymi i poruszającymi się ze stałą prędkością. Każdy z tych stanów może być naturalnym stanem ciała gdy nie ma żadnych sił. Nie ma różnicy pomiędzy sytuacją gdy nie działa żadna siła i przypadkiem gdy wypadkowa wszystkich sił jest równa zeru.
Druga zasada dynamiki Newtona
Wiemy już, że ta zasada jest słuszna gdy obserwator znajduje się w układzie inercjalnym. Siła w drugiej zasadzie dynamiki jest siłą wypadkową (trzeba brać sumę wektorową wszystkich sił).
Zastanówmy się jaka jest różnica między definicją siły, a drugą zasadą dynamiki?
Czy F = ma nie powinno być prawdziwe z definicji, a nie dlatego, że jest to podstawowe prawo przyrody?
Różnica pomiędzy równaniami (4.3b) i (4.4) polega na tym, że w tym drugim występuje siła wypadkowa. To jest ważna różnica!!! Oznacza to, że w tym równaniu jest zawarta dodatkowa informacja (którą trzeba sprawdzić doświadczalnie), a mianowicie addytywność masy i wektorowe dodawanie sił. Chociaż wydaje się to banalne, że połączenie mas m1 i m2 daje przedmiot o masie m = m1 + m2 to jak każde twierdzenie w przyrodzie musi być sprawdzone doświadczalnie. Istnieją wielkości fizyczne, które nie są addytywne np. kąty (nieprzemienne dodawanie) czy objętości mieszanin (np. woda i alkohol).
Trzecia zasada dynamiki Newtona
Załóżmy, że mamy układ, który składa się z mA i mB. Wtedy jedynymi siłami będą siły oddziaływania między tymi ciałami np. grawitacyjne.
Trzecia zasada stwierdza, że w przypadku sił oddziaływania między dwoma ciałami FA = - FB .Przykład 1
Rozważmy układ trzech ciał o masach 3m, 2m i m połączonych nitkami tak jak na rysunku. Układ jest ciągnięty zewnętrzną siłą F. Szukamy przyspieszenia układu i naprężeń nici. Siły przenoszone są przez sznurki (zakładamy, że ich masy są zaniedbywalne).
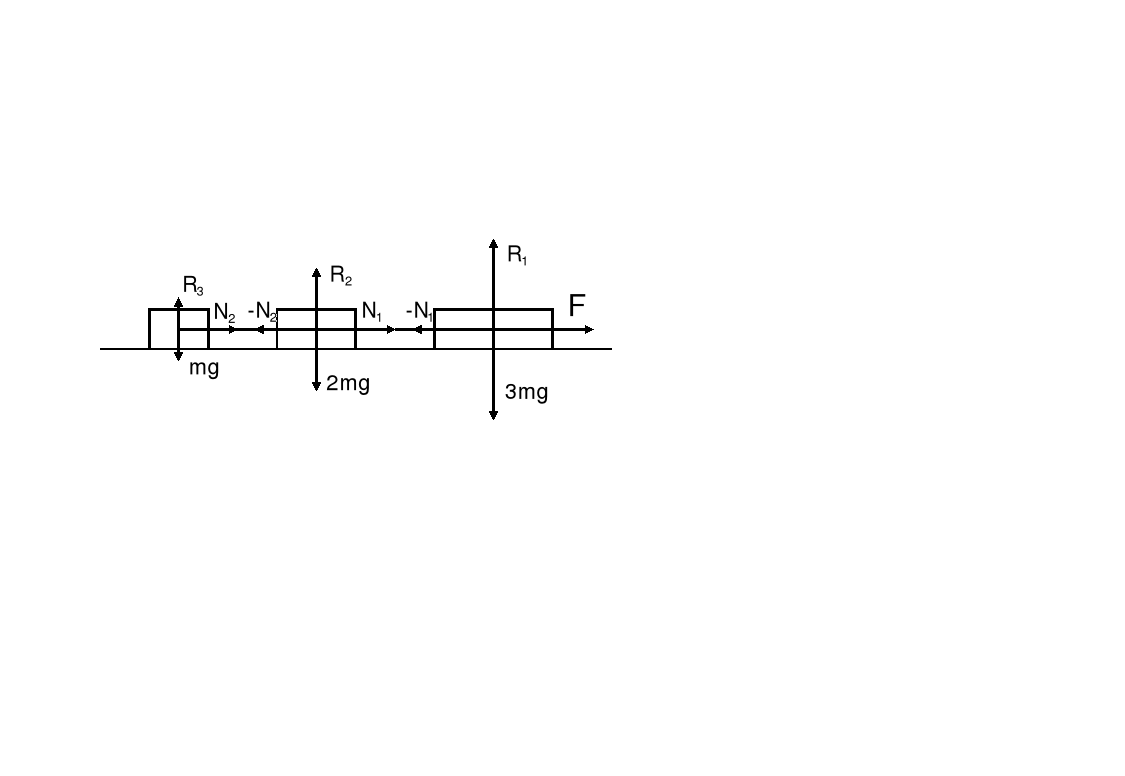
Piszemy II zasadę dynamiki dla każdego ciała osobno F - N1 = 3ma, N1 -N2 = 2ma, N2 = ma
Dodając stronami otrzymujemy F = (3m + 2m + m)a, Stąd a = F/6m, N1 = F/2, N2 = F/6
Jednostki siły i masy
W układzie SI: niuton (N) 1N = 1kg·1m/s2
11.Masa i ciężar
Masa
Definicja o charakterze operacyjnym (recepta na postępowanie). Nieznaną masę m porównujemy ze wzorcem masy 1 kg. Umieszczamy pomiędzy nimi sprężynę i zwalniamy ją. Masy, które początkowo spoczywały polecą w przeciwnych kierunkach z prędkościami v0 i v. 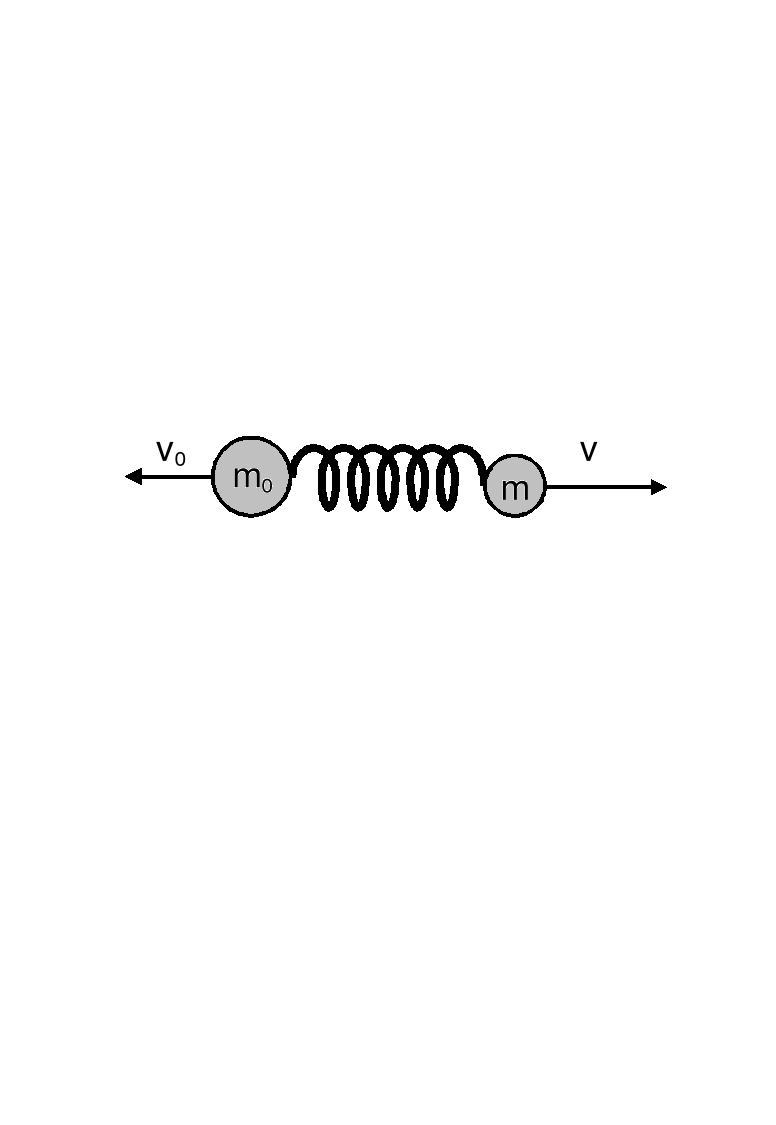
Nieznaną masę m definiujemy jako![]()
(4.1)
Ciężar
Ciężar zazwyczaj definiujemy jako siłę ciążenia działającą na ciało. W pobliżu powierzchni Ziemi dla ciała o masie m będzie ona równa mg. Na Księżycu ciężar jest mniejszy w porównaniu z ciężarem na Ziemi około sześć razy.
Definicja ciężaru może być myląca. Np. astronauta pomimo, że działa na niego jeszcze siła ciążenia uważa, że jest w stanie nieważkości. Fizjologiczne odczucie ciężaru czyli ile siły trzeba włożyć np. do podniesienia ręki.
Ciężar pozorny, masa bezwładna i masa grawitacyjna
Ważną konsekwencją tego, że siła grawitacyjna działająca na ciało jest proporcjonalna do jego masy, jest możliwość pomiaru masy za pomocą mierzenia siły grawitacyjnej. Można to zrobić używając wagi sprężynowej albo porównując siły grawitacyjne działające na masę znaną (wzorzec) i na masę nieznaną innymi słowy ważąc ciało na wadze. Powstaje pytanie czy w obu metodach mierzymy tę samą właściwość. Np. gdy spróbujemy pchnąć klocek po idealnie gładkiej poziomej powierzchni to wymaga to pewnego wysiłku, a przecież ciążenie nie pojawia się tu w ogóle. Konieczność przyłożenia siły jest związana z masą. Ta masa występuje we wzorze F = ma. Nazywamy ją masą bezwładną m. W innej sytuacji utrzymujemy ten klocek uniesiony w górę w stanie spoczynku. Bezwładność nie odgrywa tu żadnej roli bo ciało nie przyspiesza, jest w spoczynku. Ale musimy używać siły o wartości równej przyciąganiu grawitacyjnemu między ciałem i Ziemią, żeby ciało nie spadło. Odgrywa tu rolę ta właściwość ciała, która powoduje jego przyciąganie przez inne obiekty takie jak Ziemia i siła jest tu dana wzorem
![]()
gdzie m' jest masą grawitacyjną. Czy m i m' ciała są sobie równe? Masa bezwładna m1 spadając swobodnie w pobliżu powierzchni Ziemi ma przyspieszenie a1, przy czym ![]()
jeżeli inna masa m2 uzyskuje inne przyspieszenie a2 to ![]()
Dzieląc te równania przez siebie otrzymamy ![]()
Widzimy, że jeżeli wszystkie ciała spadają z tym samym przyspieszeniem a1 = a2 = g to stosunek mas bezwładnych jest równy stosunkowi mas grawitacyjnych. Jeżeli dla jednej substancji ustalimy, że masa bezwładna jest równa masie grawitacyjnej to prawdziwe to będzie dla wszystkich substancji. Aktualnie jesteśmy w stanie stwierdzić, że a1 = a2 z dokładnością 10-10. Te wyniki sugerują, że masa bezwładna jest równa masie grawitacyjnej. To stwierdzenie nazywa się zasadą równoważności.
Konsekwencją jest to, że nie można rozróżnić między przyspieszeniem układu (laboratorium), a przyspieszeniem grawitacyjnym. Ta zasada jest punktem wyjścia ogólnej teorii względności Einsteina.
12. Zastosowania zasad dynamiki ( równania, przekładnie, …)
13.Tarcie
Siły kontaktowe
Gdy dwa ciała są dociskane do siebie to występują między nimi siły kontaktowe. Źródłem tych sił jest odpychanie pomiędzy atomami. Przy dostatecznie małej odległości występuje przekrywanie chmur elektronowych i ich odpychanie rosnące wraz z malejącą odległością. To jest siła elektromagnetyczna i może być bardzo duża w porównanie z siłami grawitacyjnymi.
Jeżeli siła ciężkości pcha blok w dół siłą Fg to powstaje druga siła - siła kontaktowa F1. Siła wypadkowa Fwyp = 0. We wszystkich przypadkach stosowania drugiej zasady dynamiki Newtona jest bardzo istotne, żeby obliczyć siłę wypadkową.
Przykład 1
Rozważmy dwa klocki m1 i m2 na gładkiej powierzchni. Do klocka m1 przyłożono siłę F. Czy siła F jest przenoszona poprzez klocek 1 na klocek 2? Gdyby tak było to zgodnie z trzecią zasadą dynamiki Newtona klocek 2 działałby na klocek 1 siłą równą i przeciwnie skierowaną. Wtedy Fwyp równałaby się zero!!!!, czyli, że nie można by było poruszyć ciała 1 bez względu na to jak duża jest siła F.
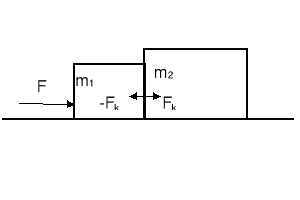
Zasada Newtona nie mówi, że siła F jest przenoszona przez klocek 1 na klocek 2; powinno się przyjąć siłę kontaktową Fk o dowolnej wartości. Ogólnie: powinno się stosować drugą zasadę dynamiki oddzielnie do każdego ciała.
Dla klocka 1 otrzymujemy wtedyF - Fk = m1a
Dla klocka 2 Fk = m2a
Stąd przyspieszenie a = F/(m1 + m2)
Zauważmy, że ten wynik można otrzymać gdy traktujemy te dwa klocki jak jedną masę m = m1 + m2.
Tarcie
Siły kontaktowe, o których mówiliśmy są normalne (prostopadłe) do powierzchni. Istnieje jednak składowa siły kontaktowej leżąca w płaszczyźnie powierzchni. Jeżeli ciało pchniemy wzdłuż stołu to po pewnym czasie ciało to zatrzyma się. Z drugiej zasady dynamiki wiemy, że jeżeli ciało porusza się z przyspieszeniem to musi działać siła. Taką siłę nazywamy siłą tarcia.
Rozważmy np. klocek, do którego przykładamy "małą" siłę F tak, że klocek nie porusza się. Oznacza to, że sile F przeciwstawia się siła tarcia T. Mamy więc: T = -F. Zwiększamy stopniowo siłę F aż klocek zaczyna się poruszać. Im gładsza powierzchnia tym szybciej to nastąpi. Oznacza to, że siła tarcia zmienia się od wartości zero do pewnej wartości krytycznej w miarę wzrostu siły F. Oznaczmy tę krytyczną siłę Ts (s-statyczna). To jest maksymalna siła tarcia statycznego.
Ts (dla pary powierzchni suchych) spełnia dwa prawa empiryczne:
Jest w przybliżeniu niezależna od powierzchni zetknięcia (w szerokim zakresie),
Jest proporcjonalna do siły normalnej (prostopadłej) z jaką jedna powierzchnia naciska na drugą.
Stosunek siły Ts do nacisku FN nazywamy współczynnikiem tarcia statycznego μs ![]()
Uwaga: Mówimy tylko o wartościach tych sił bo są one do siebie prostopadłe. Jeżeli F jest większe od Ts to klocek poruszy się, ale będzie istniała siła tarcia Tk (k - kinetyczna) przeciwstawiająca się ruchowi.
Siła Tk spełnia trzy prawa empiryczne:
Jest w przybliżeniu niezależna od powierzchni zetknięcia (w szerokim zakresie),
Jest proporcjonalna do siły normalnej (prostopadłej) z jaką jedna powierzchnia naciska na drugą,
Nie zależy od prędkości względnej poruszania się powierzchni.
Istnieje odpowiedni współczynnik tarcia kinetycznego μk ![]()
(5.2)
Dla większości materiałów μk jest nieco mniejszy od μs. Np. μk ≈ 1 dla opon na jezdni betonowej.
Tarcie jest bardzo złożonym zjawiskiem i wyjaśnienie go wymaga znajomości oddziaływań atomów na powierzchni. Nie będziemy się tym zajmować. Ograniczmy się do zauważenia, że tarcie odgrywa bardzo istotną rolę w życiu codziennym. W samochodzie np. na pokonanie siły tarcia zużywa się około 20% mocy silnika. Tarcie powoduje zużywanie poruszających się części maszyn. Staramy się je zwalczać. Z drugiej strony bez tarcia nie moglibyśmy chodzić, jeździć samochodami, trzymać ołówka, kredy, czy też nimi pisać.
14. Dynamika punktu materialnego po okręgu
15. 16. 17. Siły bezwładności. Układy inercjalne i nieinercjalne.
We wstępie wyszczególnione zostały cztery rodzaje sił występujących w przyrodzie. Wszystkie te siły nazywamy siłami rzeczywistymi, ponieważ możemy je zawsze związać z jakimś konkretnym ciałem, możemy podać ich pochodzenie. Czy to samo możemy powiedzieć np. o takich siłach jakich działania "doznajemy" np. przy przyspieszaniu, hamowaniu czy zakręcaniu samochodu?
Przykład 2
Dwaj obserwatorzy opisują ruch kulki w sytuacji pokazanej na rysunku poniżej.
Jeden z obserwatorów znajduje się w wózku a drugi stoi na Ziemi. Wózek początkowo porusza się ze stałą prędkością po linii prostej (rys. 1), następnie hamuje ze stałym opóźnieniem a (rys. 2). Między kulką a wózkiem nie ma tarcia.
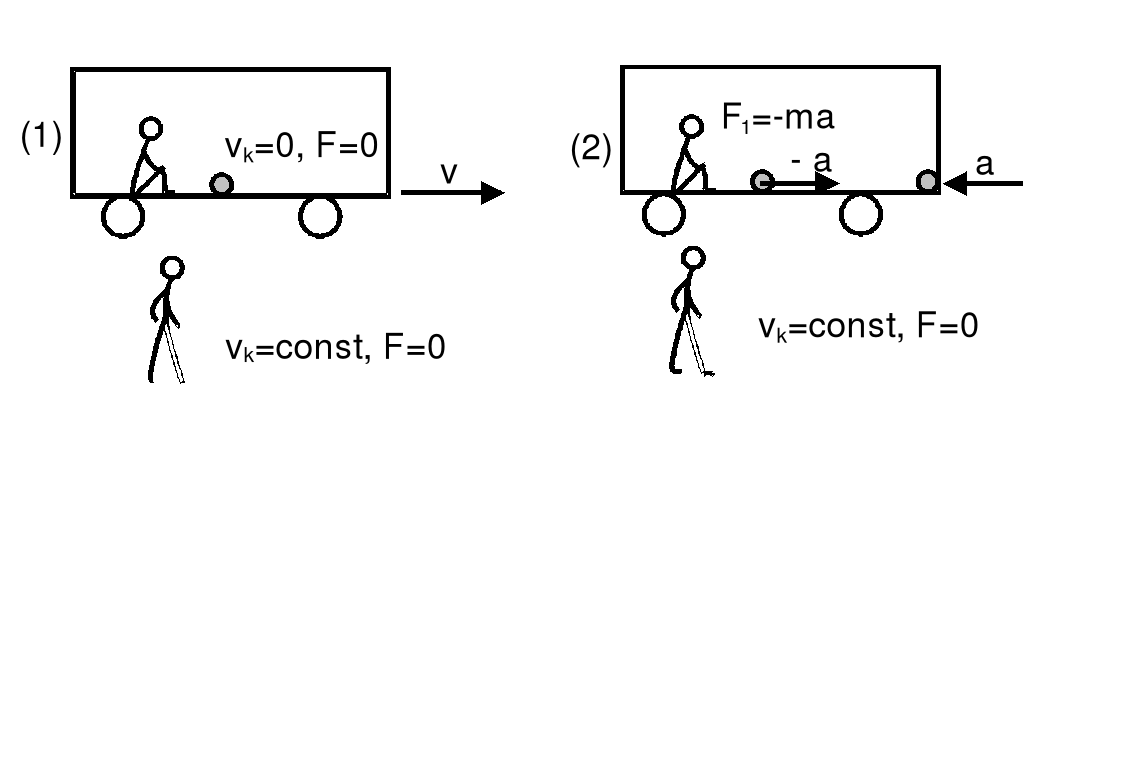
Gdy wózek jedzie ze stałą prędkością to obydwaj obserwatorzy stwierdzają zgodnie na podstawie pierwszej zasady dynamiki, że na kulkę nie działa żadna siła. Zwróćmy uwagę, że obserwatorzy znajdują się w inercjalnych układach odniesienia. Sytuacja zmienia się gdy wózek zaczyna hamować (rys. 2). Obserwator związany z Ziemią dalej twierdzi, że kulka porusza się ze stałą prędkością, a tylko podłoga wózka przesuwa się pod nim. Natomiast obserwator w wózku stwierdza, że kulka zaczyna się poruszać się z przyspieszeniem -a w stronę przedniej ściany wózka. Dochodzi do wniosku, że na kulkę o masie mk zaczęła działać siła F1 = - mka ale nie może wskazać żadnego ciała, będącego źródłem tej siły. Mówiliśmy już, że druga zasada dynamiki jest słuszna tylko w inercjalnym układzie odniesienia. Zauważmy, że obserwator w wózku znajduje się teraz w układzie nieinercjalnym. Widać, że jest w błędzie; nie istnieje rzeczywista siła F1. Jest to tak zwana pozorna siła bezwładności.
Powstaje więc pytanie jak postępować gdy musimy rozwiązać problem w układzie nieinercjalnym. W tym celu rozpatrzmy dalszy ruch kulki. Gdy dotrze ona do przedniej ścianki to wówczas według obserwatora na Ziemi (układ inercjalny) będzie poruszać się z przyspieszeniem a (takim jak wózek) bo działa na nią siła Fs sprężystości przedniej ściany wózka równa Fs = mka Natomiast obserwator w wózku stwierdza, że kulka przestała się poruszać; spoczywa względem niego. Jego zdaniem siła sprężystości ściany Fs równoważy siłę F1, tak że siła wypadkowa jest równa zeru i kulka nie porusza się Fs + F1 = 0
co po podstawieniu za F1 = - mka daje Fs = mka
Okazuje się, że wynik otrzymany przez obserwatora w układzie nieinercjalnym jest taki sam jak dla obserwatora związanego z Ziemią ale pod warunkiem uwzględnienia sił pozornych. Siły te "znikają" jeśli rozpatrujemy ruch z punktu widzenia układu inercjalnego. Wprowadzenie ich pozwala po prostu na stosowanie mechaniki klasycznej do opisu zdarzeń w układach poruszających się z przyspieszeniem. W takim układzie uwzględniamy, że na każde ciało działa siła wprost proporcjonalna do masy tego ciała, do przyspieszenia układu a i jest skierowana przeciwnie do a.
Przykład 3
Winda porusza się ruchem jednostajnie zmiennym. Czas spadania ciała puszczonego swobodnie w tej windzie, na drodze od sufitu do podłogi, jest o 25% większy niż w windzie stojącej. Obliczyć przyspieszenie windy. Dane jest przyspieszenie ziemskie g.
Rozwiązujemy zadanie w układzie inercjalnym i nieinercjalnym tzn. obserwator w jednym przypadku znajduje się na zewnątrz windy, a w drugim jest pasażerem tej windy.
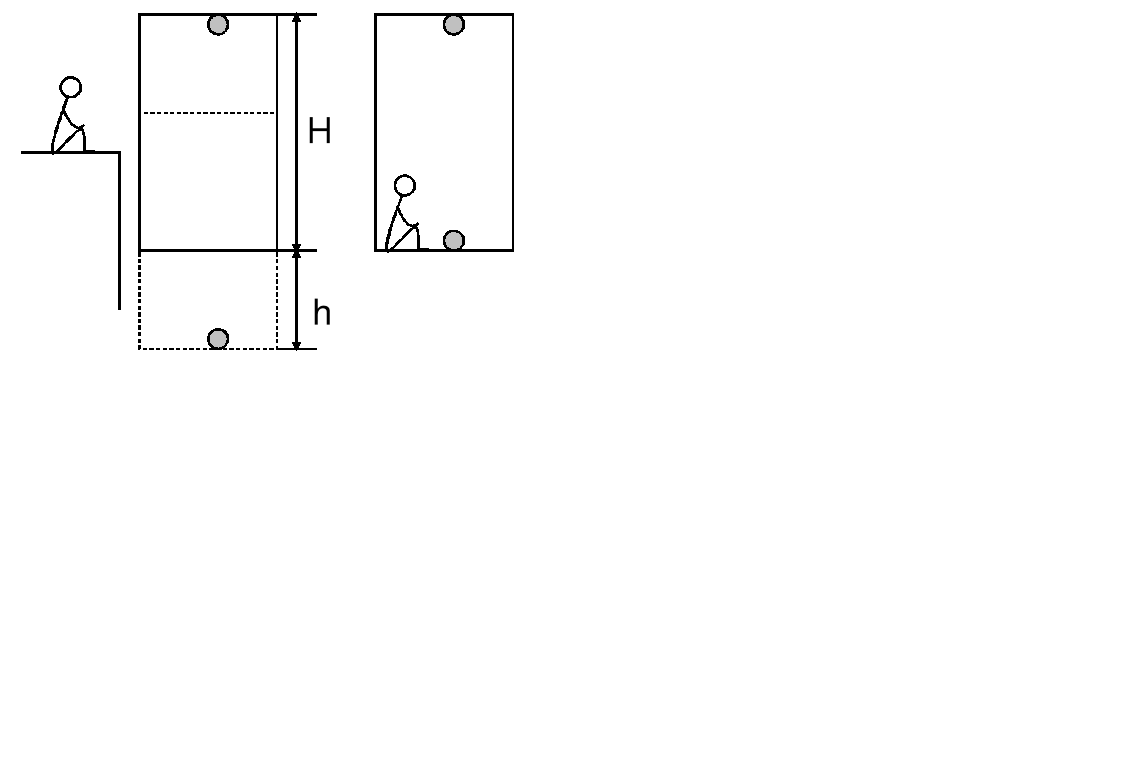
W przypadku pierwszym obserwator "widzi" (mierzy), że ciało przebywa dłuższą drogę gdy winda jest w ruchu.
Dla windy stojącej ![]()
Dla windy w ruchu ![]()
oraz![]()
przy czym
![]()
Rozwiązanie tego układu równań daje wynik ![]()
Drugi obserwator za każdym razem widzi, że ciało przebywa tę samą drogę H od sufitu do podłogi ale w różnych czasach. Wniosek: w obu przypadkach jest różne przyspieszenie. Obserwator wprowadza do obliczeń dodatkową siłę nadającą przyspieszenie -a. Odpowiednie równania wyglądają teraz:
Dla windy stojącej ![]()
Dla windy w ruchu ![]()
Uwzględniając, że ![]()
otrzymujemy ![]()
.
Tak więc uwzględnienie sił bezwładności jest konieczne jeżeli chcemy stosować zasady dynamiki w układach nieinercjalnych.
W takim układzie uwzględniamy, że na każde ciało działa siła wprost proporcjonalna do masy tego ciała, do przyspieszenia układu a i jest skierowana przeciwnie do a.
Inny przykład stanowią układy nieinercjalne poruszające się ruchem obrotowym. Np. obserwator w satelicie krążącym wokół Ziemi obserwując ciało spoczywające w tym satelicie stwierdza, że siła wypadkowa działająca na ten obiekt jest równa zeru. Musi więc istnieć, według niego, siła która równoważy siłę grawitacji (dośrodkową). Siłę tę nazywamy siłą odśrodkową i jest to siła pozorna.
Na zakończenie rozpatrzmy ruch postępowy ciała w obracającym się układzie odniesienia. Przykładem może być człowiek poruszający się po linii prostej (radialnie) od środka do brzegu karuzeli obracającej się z prędkością kątową . Na rysunku poniżej pokazana jest zmiana prędkości człowieka.
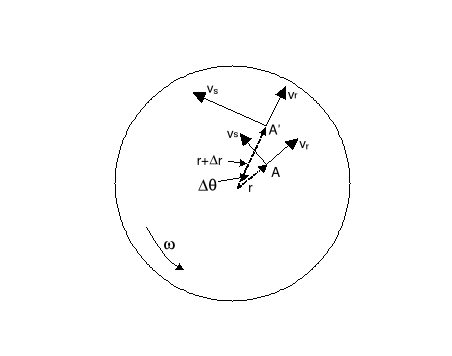
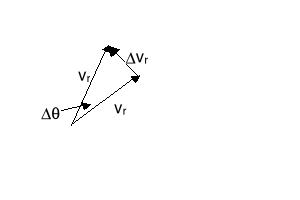
Linia (promień) wzdłuż której porusza się człowiek zmienia swój kierunek (karuzela obraca się) o kąt θ w czasie t, człowiek zmienia swoje położenie z punktu A do A'. Obliczymy teraz zmianę jego prędkości radialnej vr i stycznej vs. Prędkość radialna zmienia swój kierunek.
Prędkość styczna natomiast zmienia zarówno kierunek (przyspieszenie dośrodkowe) ale również wartość bo człowiek oddala się od środka (rośnie r). Najpierw rozpatrzmy różnicę prędkości vr w punktach A i A' pokazaną na powyższym rysunku po prawej stronie. Dla małego kąta (tzn. małego t) możemy napisać vr = vr Jeżeli obustronnie podzielimy równanie przez t to w granicy t 0 otrzymamy ![]()
Zmienia się również prędkość styczna bo człowiek porusza się wzdłuż promienia. W punkcie A prędkość styczna vs = r, a w punkcie A' vs' = (r+r). Zmiana prędkości stycznej wynosi więc vs = (r+r) - r = r Jeżeli obustronnie podzielimy równanie przez t to w granicy t 0 otrzymamy
![]()
Przyspieszenia a1 i a2 mają ten sam kierunek (równoległy do vs) więc przyspieszenie całkowite wynosi a = a1 + a2 = 2vr (5.3)
Przyspieszenie to jest nazywane przyspieszeniem Coriolisa. Pochodzi ono stąd, że nawet przy stałej prędkości kątowej rośnie prędkość liniowa człowieka bo rośnie r. Gdyby człowiek stał na karuzeli to obserwator stojący na ziemi mierzyłby tylko przyspieszenie dośrodkowe (2r) skierowane do środka wzdłuż promienia. Natomiast gdy człowiek idzie na zewnątrz to obserwator rejestruje także przyspieszenie Coriolisa (o kierunku równoległym do vs). Oczywiście musi istnieć siła działająca w tym kierunku. Jest nią w tym przypadku siła tarcia między podłogą i butami idącego człowieka.
Jednak obserwator związany z karuzelą nie widzi ani przyspieszenia dośrodkowego ani przyspieszenia Coriolisa, człowiek poruszający się wzdłuż promienia jest w stanie równowagi w układzie karuzeli. A przecież istnieje realnie odczuwalna (rzeczywista) siła tarcia. Żeby wyeliminować tę rozbieżność obserwator stojący na karuzeli wprowadza dwie siły pozorne równoważące siłę tarcia. Jedna to siła odśrodkowa, a druga to siła Coriolisa. Siła odśrodkowa działa radialnie na zewnątrz, a siła Coriolisa stycznie ale przeciwnie do vs.
Ogólnie, na ciało o masie m poruszające się ruchem postępowym z prędkością v w obracającym się układzie odniesienia działa siła bezwładności zwana siłą Coriolisa Fc
Fc = 2mv× (5.4)Wprowadzenie sił pozornych (nie umiemy pokazać ich źródła) jest konieczne aby móc stosować mechanikę klasyczną w układach nieinercjalnych.
Ziemia nie jest idealnym układem inercjalnym ponieważ wiruje. W wyniku tego obrotu w zjawiskach zachodzących na Ziemi obserwujemy siłę Coriolisa. Przykładowo, rzeki płynące na półkuli północnej podmywają silniej prawy brzeg. Również ciała spadające swobodnie odchylają się od pionu pod działaniem tej siły. W większości rozpatrywanych przez nas zjawisk można jednak zaniedbać wpływ ruchu Ziemi na ich przebieg.
18.Praca ( przykłady)
Praca wykonana przez stałą siłę
W najprostszym przypadku, siła F jest stała, a punkt porusza się w kierunku działania siły. Wtedy W = F·s = Fs cosα (7.1)(Iloczyn dwóch wektorów daje liczbę).
Zastanówmy się czy kąt α może być różny od zera? Odpowiedź jest twierdząca, bo stała siła nie musi mieć kierunku zgodnego z kierunkiem ruchu punktu materialnego. Oczywiście muszą działać jeszcze inne siły (np. ciężar, tarcie). Gdyby działała tylko jedna to i tak ciało nie musiałoby poruszać się w kierunku jej działania np. rzut ukośny (tylko grawitacja).
Wzór Fs cosα określa jedynie pracę wykonaną przy przemieszczaniu punktu przez jedną siłę. Pracę wykonaną przez inne należy obliczyć oddzielnie i potem je zsumować. Zwróćmy uwagę, że gdy α = 0 otrzymujemy pierwszy wzór Fs. Gdy α = 90° to z równania wynika, że W = 0.
Przykłady
(a) i (b) W = 0 bo α = 90°, (c) i (d) bo przesunięcie s = 0.
Jednostką pracy jest w układzie SI dżul (J), 1J = 1N·1m.
Często używa się jednostki elektronowolt 1eV = 1.6·10-19 J.
Pracę obliczamy z zależności:
W = Fs cosα
Aby obliczyć pracę musimy znaleźć F. Z warunku stałej prędkości (w kierunku poziomym)
Fcosα - T = 0
a dla kierunku pionowego Fsinα +R - mg = 0
Nacisk na podłoże (równy reakcji podłoża) wynosi mg - Fsinα,
więc siła tarcia wynosi T = μ (mg - Fsinα)
Te równania pozwalają wyliczyć F (eliminując T).
F = μmg/(cosα+μsinα)
więc praca W = Fs cosα = μmgs cosα/(cosα+μsinα)
Praca wykonana przez siłę zmienną
Rozważmy teraz siłę będącą funkcją położenia F(x), której kierunek jest zgodny z osią x. Szukamy pracy jaką wykona ta siła przy przesuwaniu ciała od położenia x1 do położenia x2. Jak skorzystać ze wzoru W = Fs cosα czyli co podstawić za F, skoro wartość jej zmienia się (rysunki poniżej)?
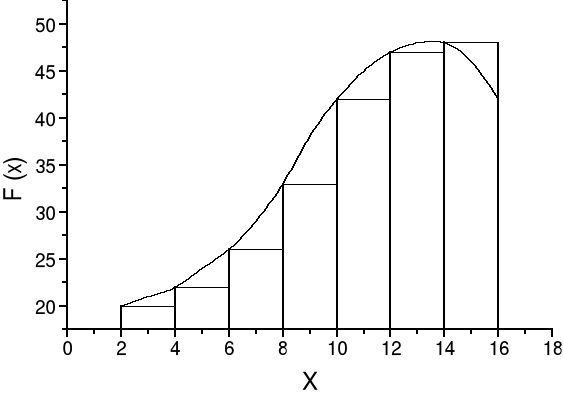
Zaczynamy od przybliżenia. Dzielimy całkowite przemieszczenie na n jednakowych odcinków Δx (rysunek poniżej). Wewnątrz takiego przedziału przyjmujemy (to jest to przybliżenie), że siła jest stała (prawie) i możemy teraz policzyć pracę na tym odcinku Δx: ΔWi = FiΔx, gdzie Fi jest wartością siły na tym odcinku. Zwróćmy uwagę, że od strony czysto formalnej (geometria) liczenie pracy jest równoważne liczeniu sumy powierzchni prostokątów o szerokości Δx i wysokości Fi. Następnie możemy zsumować prace na kolejnych odcinkach (zsumować pola prostokątów) i otrzymać pracę całkowitą.
![]()
Żeby poprawić to przybliżenie dzielimy przedział (x1, x2) na więcej (mniejszych) odcinków Δx (patrz kolejny rysunek).
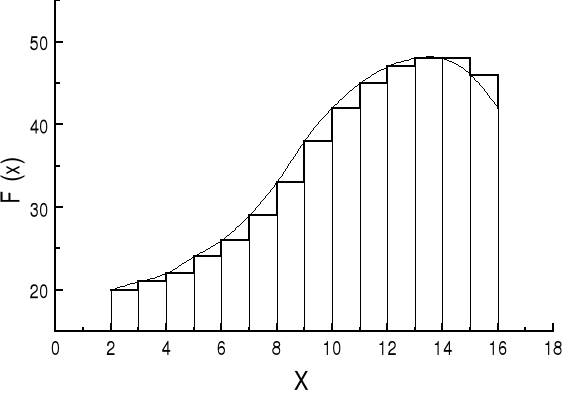
I teraz znowu powtarzamy procedurę sumowania. Przybliżenie jest lepsze bo siła ma prawie stałą wartość wewnątrz "małych" przedziałów Δx (pola powierzchni prostokątów bardziej pokrywają się z polem pod krzywą).
Widać, że rozwiązaniem problemu jest przejście (w granicy) Δx → 0.
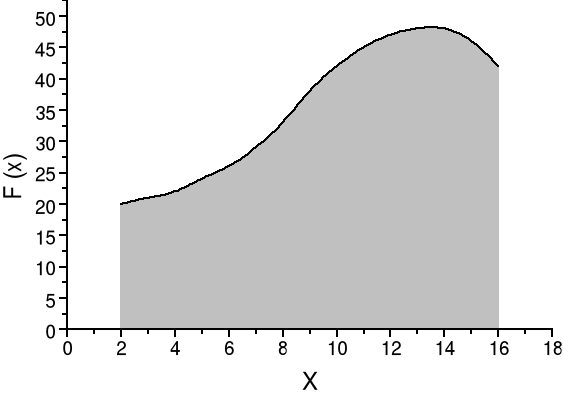
Stosujemy tę samą procedurę obliczając 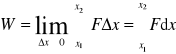
(7.2)
To jest definicja całki. Liczbowo odpowiada to liczeniu pola powierzchni pod krzywą (w zadanym przedziale - granicach). Odpowiada to też z definicji liczeniu wartości średniej co zgadza się z intuicyjnym podejściem: W = Fśrednia(x2 - x1)
Trzeba więc albo umieć rozwiązać całkę (albo poszukać w tablicach) lub umieć obliczyć pole powierzchni pod krzywą co może być czasem łatwe.
Np. rozważmy sprężynę zamocowaną jednym końcem do ściany i rozciąganą siłą F tak, że jej koniec przemieszcza się o x.
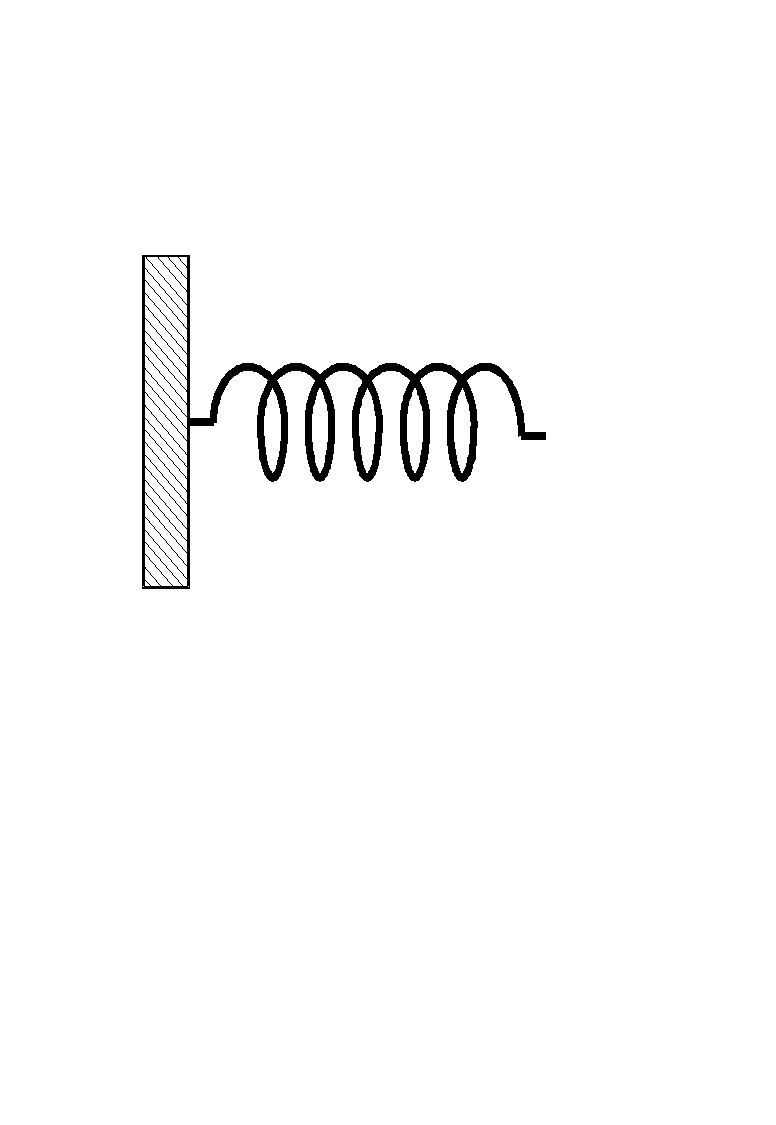
Siła wywierana przez sprężynę jest siłą przywracającą równowagę i wynosi F = -k x.
Aby rozciągnąć sprężynę musimy przyłożyć siłę równą co do wartości lecz przeciwnie skierowaną. Tak więc F = k x.
Teraz obliczmy pracę 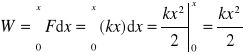
Możemy też wprost obliczyć pole pod wykresem F(x).
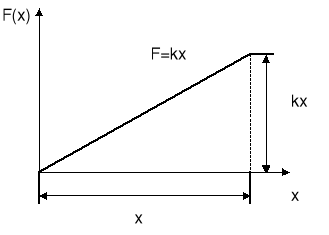
Pole powierzchni jest polem trójkąta i wynosi
P = (1/2) x·kx = (1/2) kx2
i zgadza się z wynikiem uzyskanym z obliczenia całki.
To był przypadek jednowymiarowy
19. twierdzenie o pracy i energii
W przykładzie z sankami mieliśmy do czynienia z ruchem bez przyspieszenia. Oznaczało to, że wypadkowa siła działająca na ciało wynosi zero. Teraz rozważmy przypadek gdy ciało porusza się pod wpływem niezrównoważonej siły. Najprostszy przypadek to stała siła czyli ruch ze stałym przyspieszeniem. Jaką pracę wykonuje ta siła przy przemieszczeniu ciała na odległość x?
Zakładamy, że kierunek siły F i przyspieszenia a pokrywa się z kierunkiem osi x. Dla stałego przyspieszenia mamy
![]()
oraz ![]()
co w połączeniu daje![]()
Wykonana praca jest równa
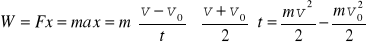
(7.3)
Połowę iloczynu masy ciała i kwadratu prędkości nazywamy energią kinetyczną.
Praca wykonana przez wypadkową siłę F działającą na punkt materialny jest równa zmianie energii kinetycznej tego punktu.
W = Ek - Ek0 (7.4)
To jest twierdzenie o pracy i energii.
Gdy nie ma zmiany wartości prędkości to nie ma zmiany energii kinetycznej tzn. nie jest wykonywana praca (np. siła dośrodkowa). Z twierdzenia powyższego wynika, że jednostki pracy i energii są takie same.
20. Moc
Rozważmy czas w jakim wykonywana jest praca. Często interesuje nas szybkość wykonania pracy a nie jej wartość. To jest właśnie moc.
Moc średnia: Pśrednia = W/t
Moc chwilowa: P = dW/dt
Oczywiście gdy moc jest stała w czasie to Pśrednia = P.
Jednostką mocy jest wat. 1W = 1J/1s.
Dla celów praktycznych używa się kW (kilowatów) lub KM (koni mechanicznych przy czym 1 KM ≈ (3/4) kW.
21. Energia potencjalna
Skupimy się teraz na odosobnionym układzie ciało + sprężyna. Zamiast mówić ciało się porusza będziemy mówić: stan układu się zmienia.
gdy nie występuje tarcie to energia kinetyczna maleje a potem rośnie tak, że wraca do początkowej wartości w cyklu zamkniętym. W tej sytuacji (gdy działają siły zachowawcze) staje się celowe wprowadzenie pojęcia energii stanu lub energii potencjalnej Ep. Mówimy, że jeżeli energia kinetyczna układu zmieni się o wartość ΔEk to tym samym zmienił się stan układu to energia potencjalna Ep (stanu) tego układu musi się zmienić o wartość równą co do wartości bezwzględnej, lecz przeciwną co do znaku, tak że suma tych zmian jest równa zeru
ΔEk + ΔEp = 0
każda zmiana energii kinetycznej Ek jest równoważona przez równą co do wartości, a przeciwną co do znaku zmianę energii potencjalnej Ep układu, tak że ich suma pozostaje przez cały czas stała Ek + Ep. = const. (8.1)
Energia potencjalna przedstawia formę nagromadzonej energii, która może być całkowicie odzyskana i zamieniona na energię kinetyczną. Nie można więc wiązać energii potencjalnej z siłą niezachowawczą.
W przykładzie ze sprężyną (bez tarcia) energia kinetyczna ciała początkowo maleje, a zlokalizowana w sprężynie energia potencjalna rośnie. Z twierdzenia o pracy i energii
W = ΔEk więc dla zachowawczej siły F , W = ΔEk = - ΔEp
Stąd 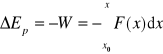
(8.2)
Możemy więc zapisać zależność między siłą i energią potencjalną
![]()
(8.3)
Trzeba zwrócić uwagę, że naprawdę potrafimy tylko policzyć ΔEp a nie Ep samą. Ponieważ ΔEp = EpB - EpA. Żeby znaleźć EpB trzeba nie tylko znać siłę ale jeszcze wartość EpA
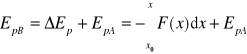
Punkt A nazywamy punktem odniesienia i zazwyczaj wybieramy go tak (umowa), żeby Ep było równe zeru w tym punkcie (porównanie z potencjałem elektrycznym).
Przykłady energii potencjalnej dla jednowymiarowych sił zachowawczych
grawitacyjna energia potencjalna (w pobliżu powierzchni Ziemi)
Ruch wzdłuż osi y , F(y) = -mg
F jest stała. Przyjmujemy, że dla y = 0, Ep(0) = 0.
Wtedy 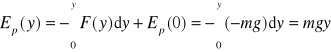
Sprawdzenie ![]()
energia potencjalna sprężyny
Ruch wzdłuż osi x, F(x) = -kx
Przyjmujemy dla x = 0, Ep(0) = 0.
Wtedy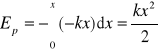
Sprawdzenie: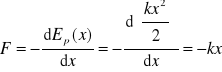
22. 23. Siły zachowawcze i niezachowawcze.
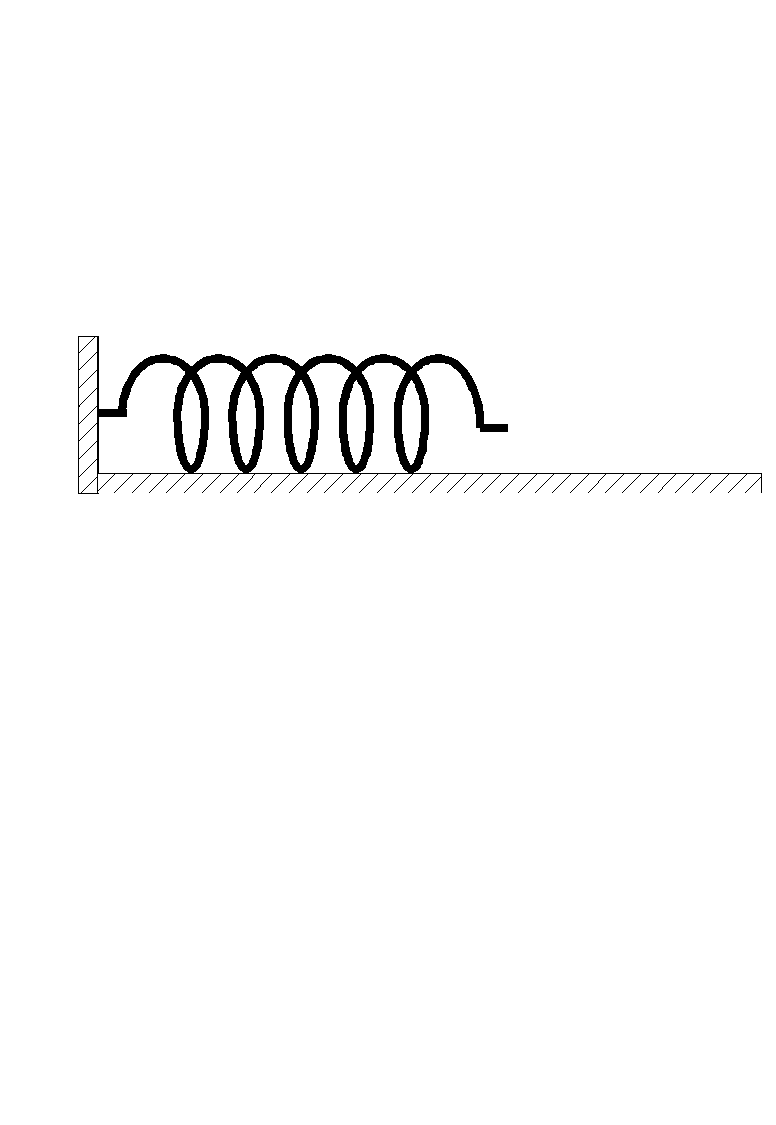
.
Przesuwamy ciało o masie m z prędkością v w kierunku sprężyny, tak jak na rysunku.
Założenia:
ruch na płaszczyźnie odbywa się bez tarcia,
sprężyna jest idealna tzn. spełnia ona prawo Hooke'a: F = -kx, gdzie F jest siłą wywieraną przez sprężynę kiedy jej swobodny koniec jest przemieszczony na odległość x,
masa sprężyny jest zaniedbywalnie mała w porównaniu z masą ciała, więc cała energia kinetyczna w układzie sprężyna + ciało jest zgromadzona w tym ciele.
Przy ściskaniu sprężyny, prędkość ciała, a wobec tego i energia kinetyczna maleje aż do zatrzymania ciała. Następnie ciało porusza się w przeciwnym kierunku pod wpływem sprężyny. Prędkość i energia kinetyczna rosną aż do wartości jaką ciało miało początkowo. Interpretowaliśmy energię kinetyczną jako zdolność ciała do wykonania pracy kosztem jego ruchu (kosztem Ek). Po przebyciu zamkniętej drogi (cyklu) zdolność ciała do wykonania pracy pozostaje taka sama, jest zachowana. Siła sprężysta wywierana przez idealną sprężynę jest zachowawcza. Inne siły, działają także w ten sposób, np. siła grawitacji. Ciało rzucone do góry, przy zaniedbaniu oporu powietrza, wróci z tą samą prędkością i energią kinetyczną.
Jeżeli jednak ciało, na które działa jedna lub więcej sił powraca do położenia początkowego i ma inną energię kinetyczną niż na początku to oznacza, że po przebyciu drogi zamkniętej zdolność tego ciała do wykonania pracy nie została zachowana. Oznacza to, że przynajmniej jedną z działających sił określa się jako niezachowawczą.
Ogólnie: Siła jest zachowawcza, jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza się po dowolnej drodze zamkniętej jest równa zeru. Siła jest niezachowawcza jeżeli praca wykonana przez tę siłę nad punktem materialnym, który porusza się po dowolnej drodze zamkniętej nie jest równa zeru.
Jeżeli siła jest zachowawcza to WAB,1 + WBA,2 = 0 bo droga zamknięta. Możemy to zapisać inaczej WAB,1 = - WBA,2
Siłę nazywamy zachowawczą jeżeli praca wykonana przez nią nad punktem materialnym poruszającym się między dwoma punktami zależy tylko od tych punktów, a nie od łączącej je drogi. Siłę nazywamy niezachowawczą jeżeli praca wykonana przez nią nad punktem materialnym poruszającym się między dwoma punktami zależy od drogi łączącej te punkty.
Przedstawione definicje są równoważne.
24.Zasada zachowania energii mechanicznej
Zasada zachowania energii Gdy działają siły zachowawcze to W = ΔEk = EkB - EkA
Oraz W = -ΔEp = - (EpB - EpA)
Więc - (EpB - EpA) = EkB - EkA
czyli EkA + EpA = EkB + EpB (8.7)
Równania (8.1, 8.4) nazywa się zasadą zachowania energii mechanicznej.
Mówi ona, że dla ciała podlegającego działaniu siły zachowawczej, którego energia potencjalna jest równa Ep, suma energii kinetycznej i potencjalnej jest stała (o ile nie działają inne siły).
A co z zachowaniem energii w przypadku gdy działa siła niezachowawcza?
Dla sił zachowawczych ![]()
lub ![]()
Wielkość po lewej stronie to po prostu zmiana całkowitej energii mechanicznej ΔE. Zatem równanie to ma postać ΔE = 0.
Jeżeli oprócz kilku sił zachowawczych działa siła niezachowawcza (np. tarcie) to wtedy ![]()
czyli ![]()
co jest równoważne ![]()
Widać, że siła tarcia zmienia energię mechaniczną układu (zmniejsza ją bo tarcie jest siłą rozpraszającą czyli dysypatywną).
Co stało się ze "straconą" energią mechaniczną?
Zostaje ona przekształcona na energię wewnętrzną U, która objawia się wzrostem temperatury. U jest równa rozproszonej energii mechanicznej. Fwyp = Fzew + FZ + FNZ
Z twierdzenia o pracy i energii wynika, że praca wykonana przez siłę wypadkową jest równa zmianie energii kinetycznej.![]()
co jest równoważne Wzew - ΔEp - ΔU = ΔEk
Czyli Wzew = ΔEk + ΔEp + ΔU(8.8)
Z równania (8.5) wynika, że każda praca wykonana na ciele przez czynnik zewnętrzny równa się wzrostowi energii kinetycznej plus wzrost energii potencjalnej plus wzrost energii wewnętrznej. Cała energia została zarejestrowana. Mamy obejmujące wszystko zachowanie energii (całkowitej).
Wynika z niego, że energia może być przekształcona z jednej formy w inną, ale nie może być wytwarzana ani niszczona; energia całkowita jest wielkością stałą.
Przykład
Energia i samochód.
Samochód jedzie z prędkością 100 km/h i zużywa 8 litrów benzyny na 100 km. Jaka moc jest potrzebna do utrzymania tej stałej prędkości?
1 litr benzyny - 3.7·107 J więc P = (8·3.7·107 J)/(3600s) = 7·104 W = 70 kW.
Dla porównania w mieszkaniu zużywamy około 1 - 1.5 kW energii elektrycznej.
Samochód zużywa kilkadziesiąt razy więcej.
25.Środek masy i ruch środka masy
Środek masy
Dotychczas przedmioty traktowaliśmy jak punkty materialne, tzn. cząsteczki bezwymiarowe (objętość = 0) obdarzone masą co wystarczało w przypadku ruchu postępowego bo ruch jednego punktu odzwierciedlał ruch całego ciała.
W ogólnym przypadku ruch układu cząsteczek może być bardzo skomplikowany np.
ciało może wirować lub drgać.
w trakcie ruchu cząsteczki mogą zmieniać swoje wzajemne położenie.
środek masy jest po prostu średnim położeniem przy czym masa jest czynnikiem ważącym przy tworzeniu średniej.
Np. dla dwóch różnych mas m1 i m2
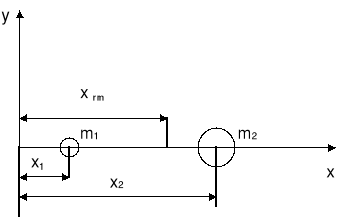
![]()
czyli ![]()
Dla n mas leżących wzdłuż linii prostej otrzymamy
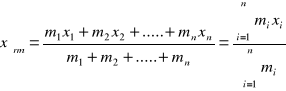
ponieważ suma ![]()
jest całkowitą masą układu to możemy zapisać ![]()
Gdyby punkty nie leżały na jednej prostej to wówczas środek masy znajdziemy postępując dla każdej ze współrzędnych analogicznie jak powyżej.
Otrzymamy więc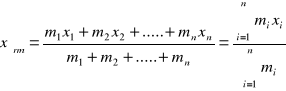
oraz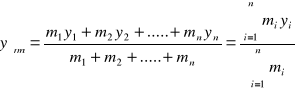
Zwróćmy uwagę, że układ dwóch równań skalarnych można zastąpić przez jedno zwięzłe równanie wektorowe 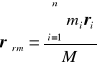
(9.1)
Uogólnienie na trzy wymiary jest automatyczne.
Zauważmy, że środek masy układu punktów materialnych zależy tylko od mas tych punktów i od wzajemnego ich rozmieszczenia (nie zależy od wyboru układu odniesienia).
Ruch środka masy
Rozważmy układ punktów materialnych o masach m1, m2, m3 ..., mn i o stałej całkowitej masie M. Na podstawie równania (9.1) możemy napisać
Mrśrm = m1r1 + m2r2 +.......+ mnrn
gdzie rśrm jest środkiem masy w określonym układzie odniesienia. Różniczkując (względem czasu) powyższe równanie otrzymamy
![]()
lub Mvśrm = m1v1 + m2v2 +.....+ mnvn
Jeżeli ponownie zróżniczkujemy otrzymane powyżej równanie to otrzymamy
![]()
lub Maśrm = m1a1 + m2a2 + .......+ mnan
czyli Maśrm = F1 + F2 + ...........+ Fn
Wobec tego możemy napisać Maśrm = Fzew (9.2)
Z równania (9.2) wynika, że środek masy układu punktów materialnych porusza się w taki sposób, jakby cała masa układu była skupiona w środku masy i jakby wszystkie siły zewnętrzne nań działały.
To twierdzenie obowiązuje dla każdego układu punktów materialnych.
Układ może być ciałem sztywnym (punkty mają stałe położenia względem siebie). Wtedy przy obliczeniach środka masy sumowanie zastępujemy całkowaniem.
Układ może być zbiorem cząsteczek, w którym występują wszystkie rodzaje ruchu wewnętrznego.
Uwaga:
Gdy siłą zewnętrzną jest siła ciężkości to wtedy działa ona na środek ciężkości. W rozważanych przypadkach te dwa środki się pokrywają.
Pojęcie środka masy jest bardzo użyteczne np. do obliczania energii kinetycznej. Obliczmy Ek mierzone w układzie środka masy.
![]()
gdzie vwzgl jest prędkością mierzoną w układzie środka masy. Wykonując mnożenie skalarne otrzymamy![]()
Ponieważ wyraz drugi równa się iloczynowi M razy prędkość środka masy (Mvśrm = m1v1 + m2v2 +.....+ mnvn). W układzie środka masy, w którym mierzymy, vśrm = 0 więc drugi wyraz znika.
Zatem ![]()
gdzie Ek' jest energią kinetyczną mierzoną w układzie środka masy. Dla ciał sztywnych to równanie przyjmuje postać ![]()
gdyż w układzie środka masy ciało sztywne może mieć tylko energię rotacyjną (obrotową).
26.Pęd puktu materialnego
Pęd układu punktów materialnych
pęd punktu materialnego jako iloczyn jego masy m i prędkości v. II zasada dynamiki Newtona ma postać ![]()
Przypuśćmy jednak, że zamiast pojedynczego punktu mamy do czynienia z układem n punktów materialnych o masach m1, ......, mn. Zakładamy, że masa układu (M) pozostaje stała. Każdy punkt będzie miał pewną prędkość i pewien pęd. Układ jako całość będzie miał całkowity pęd P w określonym układzie odniesienia będący sumą geometryczną pędów poszczególnych punktów w tym układzie odniesienia
P = p1 + p2 + ......... + pn
Jeżeli porównamy tę zależność z równaniem Mvśrm = m1v1 + m2v2 +.....+ mnvn
to otrzymujemy P = Mvśrm
Treść tego równania można wyrazić następująco: Całkowity pęd układu punktów materialnych jest równy iloczynowi całkowitej masy układu i prędkości jego środka masy. Ponieważ Fzew = Maśrm, to II zasada dynamiki Newtona dla układu punktów materialnych przyjmuje postać
![]()
(9.3) bo ![]()
27. Zasada zachowania pędu
Przypuśćmy, że suma sił zewnętrznych działających na układ jest równa zeru. Wtedy na podstawie równania (9.3) ![]()
Zasada zachowania pędu: Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru, całkowity wektor pędu układu pozostaje stały.
Zobaczymy jak ta zasada stosuje się do różnych sytuacji fizycznych. Omówimy teraz pojęcie sił zewnętrznych dla danego układu - jak wybrać układ i jak stosować zasadę zachowania pędu.
Przykład
Rozważmy dwa ciała o masach mA i mB połączone nieważką sprężyną umieszczone na doskonale gładkim stole. Odciągamy od siebie te ciała na pewną odległość, a następnie puszczamy swobodnie (rysunek).
ruch tych ciał.
rozważany układ tworzą go obie masy + sprężyna. Jeżeli tak to nie działa żadna siła zewnętrzna (działają siły wewnętrzne). Możemy zastosować zasadę zachowania pędu. Przed zwolnieniem ciał pęd układu (w odniesieniu do stołu) był równy zeru. I taki pozostaje po ich zwolnieniu. Chociaż ciała poruszają się ich pęd może być równy zeru, ponieważ pęd będący wielkością wektorową jest sumą dodatniego pędu ciała A (porusza się w kierunku +x) i ujemnego pędu ciała B (porusza się w kierunku -x). Z zasady zachowania pędu
pęd początkowy = pęd końcowy 0 = mAvA + mBvB
Zatem mBvB = - mAvA lub vA = - mBvB/mA
28. Układy o zmiennej masie
29.Rodzaje zderzeń
Siły działające przez krótki czas w porównaniu do czasu obserwacji układu nazywamy siłami impulsowymi. Takie siły działają w czasie zderzeń np. uderzenie piłki o ścianę czy zderzenie kul bilardowych. Ciała w trakcie zderzenia nie muszą się "dotykać", a i tak mówimy o zderzeniu np. zderzenie cząstki alfa (4He) z jądrem jakiegoś pierwiastka (np. Au). Wówczas mamy do czynienia z odpychaniem elektrostatycznym.
Wszystkie te "zdarzenia" posiadają cechy charakterystyczne dla zderzeń:
można wyraźnie rozróżnić czas "przed zderzeniem" i "po zderzeniu"
prawa zachowania pędu i energii pozwalają zdobyć wiele informacji o procesach na podstawie tego co "przed zderzeniem" i tego co "po zderzeniu" mimo, że niewiele wiemy o siłach "podczas" zderzenia.
Zderzenia w przestrzeni jednowymiarowej
wiemy, że musi być spełniona zasada zachowania pędu (siły zewn. = 0), oraz zasada zachowania energii całkowitej.
Zderzenia klasyfikujemy zwykle na podstawie tego, czy energia kinetyczna jest zachowana podczas zderzenia czy też nie. Jeżeli tak to zderzenie nazywamy sprężystym, jeżeli nie to niesprężystym.
Jedyne prawdziwe zderzenia sprężyste (chociaż nie zawsze) to zderzenia między atomami, jądrami i cząsteczkami elementarnymi. Zderzenia między ciałami są zawsze w pewnym stopniu niesprężyste chociaż czasami możemy je traktować w przybliżeniu jako sprężyste. Kiedy dwa ciała po zderzeniu łączą się mówimy, że zderzenie jest całkowicie niesprężyste. Np. zderzenie między pociskiem i drewnianym klockiem gdy pocisk wbija się w klocek.
Rozpatrzmy teraz zderzenie sprężyste w przestrzeni jednowymiarowej. Wyobraźmy sobie dwie gładkie nie wirujące kule, poruszające się wzdłuż linii łączącej ich środki. Masy kul m1 i m2, prędkości przed zderzeniem v1 i v2 a po zderzeniu u1 i u2 tak jak na rysunku poniżej.
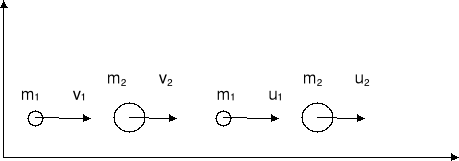
Z zasady zachowania pędu otrzymujemy
m1v1 + m2v2 = m1u1 + m2u2 (10.5)
Ponieważ zderzenie jest sprężyste to energia kinetyczna jest zachowana (zgodnie z definicją). Otrzymujemy więc ![]()
(10.6), Przepisujemy równanie (10.5) w postaci
m1(v1 - u1) = m2(u2 - v1) (10.7) a równanie (10.6) w postaci ![]()
(10.8)
Dzieląc równanie (10.8) przez równanie (10.7) otrzymamy w wyniku (przy założeniu v1 ≠ u1 i v2 ≠ u2) v1 + u1 = v2 + u2, a po uporządkowaniu v1 - v2 = u2 - u1 (10.9)
Równanie to mówi nam, że w opisanym zderzeniu względna prędkość zbliżania się cząstek przed zderzeniem jest równa względnej prędkości ich oddalania się po zderzeniu.
chcemy znaleźć u1 i u2. Wystarczą więc dowolne dwa. Biorąc dwa liniowe równania (10.7) i (10.9) obliczmy 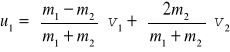
(10.10) oraz 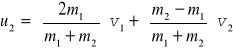
(10.11)
Przy zderzeniach niesprężystych energia kinetyczna nie jest zachowana.
Różnica pomiędzy energią kinetyczną początkową i końcową przechodzi np. w ciepło lub energię potencjalną deformacji.
31.Pęd i popęd
32. Przykład 2- wymiarowy zderzeń kul bilardowych
33. 34. Wielkości w ruchu obrotowym. Związki między wielkościami liniowymi a kątowymi w ruchu kołowym
Dla ruchu obrotowego wielkością analogiczną do przesunięcia jest przesunięcie kątowe θ. Kąt θ określa położenie punktu względem układu odniesienia. Dla ruchu po okręgu, z definicji miary łukowej kąta θ = S/R. (w radianach).
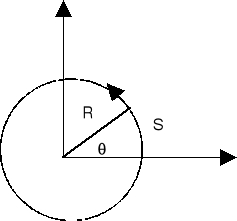
Kątową analogią prędkości v = dx/dt jest prędkość kątowa ω. ![]()
(12.1)
Dla ruchu po okręgu v = ω R.
W przypadku ruchu jednostajnego po okręgu ω jest nazywane częstością kątową i jest związana z częstotliwością f relacją ω = 2πf
Podobnie jak przyspieszenie liniowe a = dv/dt zostało zdefiniowane przyspieszenie kątowe α.
![]()
Dla ruchu po okręgu związek pomiędzy a i α jest analogiczny do związku pomiędzy v i ω tzn. a = αR. Możemy teraz np. podać opis ruchu obrotowego ze stałym przyspieszeniem α poprzez analogię do ruchu postępowego jednostajnie zmiennego
Ruch postępowy |
Ruch obrotowy |
a = const v = v0 + at s = s0 + v0t + (1/2)at2 |
α = const ω = ω0 + αt θ =θ0 + ω0t + (1/2)αt2 |
Kierunek i zwrot wektorów prędkości kątowej i przyspieszenia kątowego w ruchu obrotowym przyspieszonym (1) i opóźnionym (2) są pokazane na rysunku poniżej.
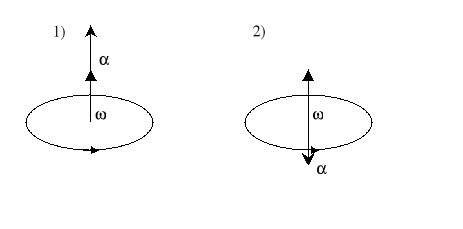
35. Moment siły. Moment pędu
W ruchu postępowym siłę wiążemy z liniowym przyspieszeniem ciała. ie może być to tylko siła bo jak pokazuje doświadczenie np. z otwieraniem drzwi przyspieszenie kątowe zależy od tego gdzie i pod jakim kątem jest przyłożona siła. W szczególności siła przyłożona w miejscu zawiasów zarówno wzdłuż jak i prostopadle do nich nie wytwarza żadnego przyspieszenia. Natomiast siła przyłożona do drzwi na ich zewnętrznej krawędzi i pod kątem prostym nadaje im maksymalne przyspieszenie.
Dla ruchu obrotowego odpowiednikiem siły w ruchu postępowym jest moment siły (tzw. moment obrotowy) τ.
Jeżeli siła F działa na cząstkę to moment siły jest definiowany jako ![]()
gdzie wektor r reprezentuje położenie cząstki względem wybranego inercjalnego układu odniesienia. Moment siły jest wielkością wektorową, której wartość bezwzględna wynosi: τ = rFsinθ (iloczyn wektorowy). Wielkość r nazywamy ramieniem siły (widać, że bierzemy albo r⊥ albo F⊥).
Moment pędu
Wielkość L będziemy nazywać momentem pędu i definiujemy ją ![]()
(12.4)
gdzie p jest pędem cząstki, a r reprezentuje położenie cząstki względem wybranego inercjalnego układu odniesienia. Wartość L wynosi rpsinθ i analogicznie do momentu siły wielkość rsinθ nazywamy ramieniem pędu.
Istnieje bezpośrednia zależność pomiędzy momentem siły i momentem pędu. Zacznijmy od znanej zależności, że siła F = dp/dt (dla pojedynczej cząstki). Mnożąc wektorowo obie strony przez r otrzymujemy ![]()
![]()
jest momentem siły τ więc ![]()
Teraz przechodzimy do równania na moment pędu L = r×p i różniczkujemy je obustronnie względem czasu, otrzymując ![]()
ponieważ dr/dt = v więc ![]()
Wiemy, że ![]()
= 0 (z definicji iloczynu wektorowego), więc ![]()
Porównanie równań (12.5) i (12.6) prowadzi do wniosku, że ![]()
(12.7)
Widzimy, że wypadkowy moment siły działający na cząstkę jest równy prędkości zmian momentu pędu tej cząstki.
36. Układy punktów materialnych materialnych bryłowa sztywna.
37.38. Moment bezwładności i energia kinetyczna ruchu obrotowego.
Ciała sztywne i moment bezwładności
Przez ciała stałe, sztywne, rozumiemy ciała, w których odległość między dwoma wybranymi elementami pozostaje stała.
Zauważmy, że różne części ciała mają różną prędkość liniową v chociaż tą samą kątową ω. Dla potrzeb opisu ciało możemy podzielić na elementy o masie Δmi odległe od osi obrotu o ri. Wtedy prędkość takiego elementu wynosi vi = riω.
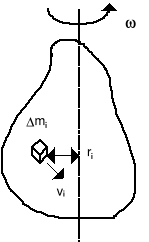
Wartość momentu pędu L tego ciała można obliczyć
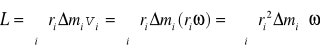
Wielkość w nawiasie nazywamy momentem bezwładności I, który definiujemy jako
![]()
a dla ciągłego rozkładu masy mamy ![]()
Zwróćmy uwagę, że I zależy od osi obrotu. Możemy teraz zapisać moment pędu
L = Iω (12.10) a ponieważ τ = dL/dt więc ![]()
(12.11)
Energia kinetyczna w układzie środka masy
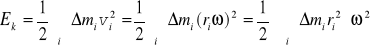
więc![]()
(12.12)
Zestawmy teraz obliczone wielkości z ich odpowiednikami dla ruchu postępowego.
Ruch postępowy |
Ruch obrotowy |
p = mv F = ma Ek = (1/2) mv2 |
L= Iω τ = Iα Ek = (1/2)Iω2 |
Teraz widzimy, że moment bezwładności I jest analogiczną wielkością do masy m w ruchu postępowym. Chociaż masa ciała nie zależy od jego położenia to moment bezwładności zależy od osi, wokół której obraca się ciało. Momenty bezwładności niektórych ciał są podane w tabeli.
Ciało |
I |
Obręcz, pierścień względem osi ⊥ przez środek Krążek, walec względem osi ⊥ przez środek Pręt wokół osi ⊥ przez środek Pręt wokół osi ⊥ przez koniec Pełna kula wokół osi przez środek Czasza kulista wokół osi przez środek |
mR2 mR2/2 ml2/12 ml2/3 2mR2/5 2mR2/3 |
Często do obliczania momentu bezwładności wygodnie jest posłużyć się twierdzeniem Steinera. Podaje ono zależność pomiędzy momentem bezwładności I ciała względem danej osi, a momentem bezwładności Iśr.m. tego ciała względem osi przechodzącej przez jego środek masy i równoległej do danej. I = Iśr.m. + md2 (12.13)
gdzie m jest masą ciała, a d odległością pomiędzy osiami.
39. Dynamika ciała sztywnego
40. Praca przy obrocie bryły.
41.Zasada zachowania momentu pędu, przykłady.
Dla układu n cząstek możemy zsumować równanie ![]()
po wszystkich cząstkach
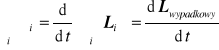
(12.8)(d15)
jeżeli na układ nie działa zewnętrzny moment siły (lub suma = 0) to moment pędu układu pozostaje stały.![]()
Przykład
Rower jedzie ze stałą prędkością gdy siła działająca pomiędzy nawierzchnią i kołem F2 = 4 N. Z jaką siłą F1 łańcuch musi ciągnąć zębatkę jeżeli stosunek R2/R1 = 10?
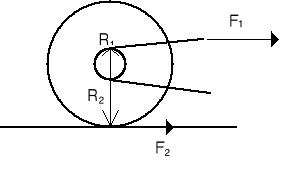
Ponieważ prędkość kątowa jest stała więc dL/dt = 0 i co za tym idzie τwypadkowy = (τ1 - τ2) = 0
Czyli τ1 = τ2 Stąd R1F1 = R2F2 więc F1 = (R2/R1)F2 = 40N
42.Podstawy działania żyroskopów ( precesja, nutacja)
Ruch precesyjny (bąk)
Inny przykładem ruchu obrotowego, w którym oś obrotu nie jest nieruchomą w inercjalnym układzie odniesienia jest bąk wirujący dookoła pewnej osi symetrii. Punkt podparcia bąka znajduje się w początku inercjalnego układu odniesienia. Z doświadczenia wiemy, że oś wirującego bąka porusza się dookoła osi pionowej, zakreślając powierzchnię stożka. Taki ruch nazywamy precesją.
W sytuacji przedstawionej na rysunku poniżej bąk ma prędkość kątową ω dookoła swej osi. Ma również moment pędu L względem tej osi, która tworzy kąt θ z osią pionową.
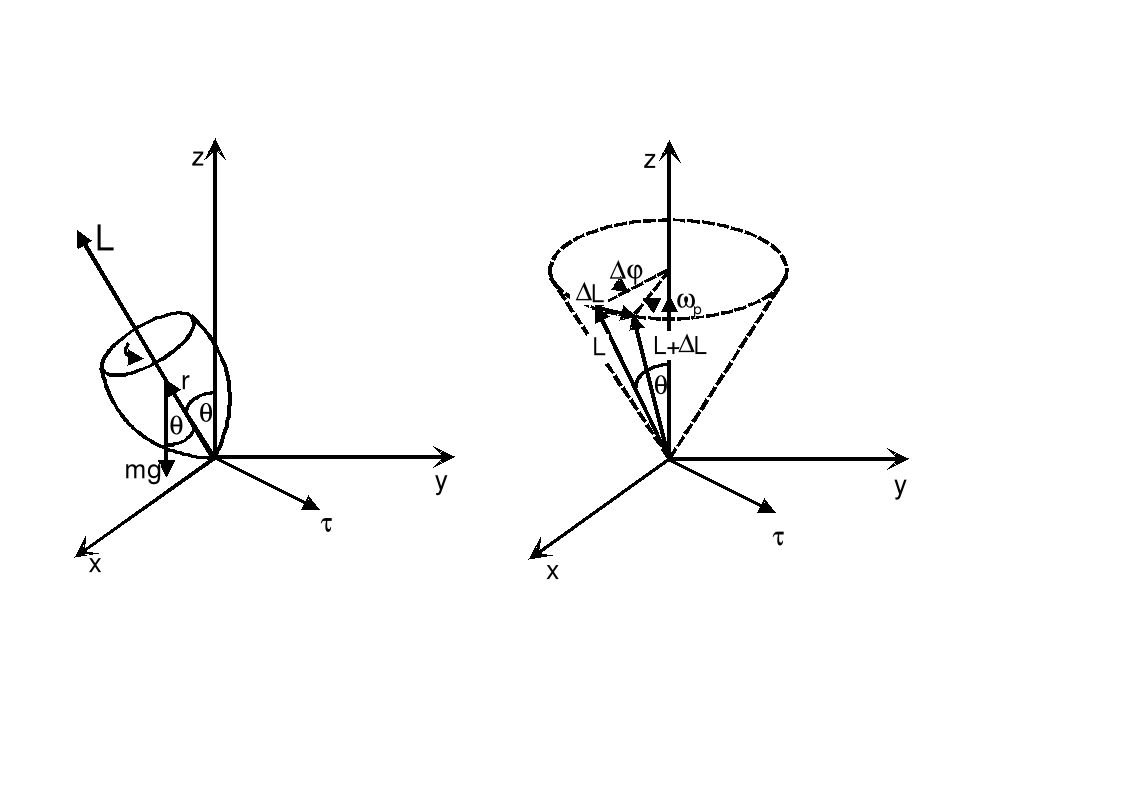
Na bąk działają dwie siły: siła w punkcie podparcia działa w górę i siła ciężkości przyłożona do środka masy działa w dół. Siła reakcji działająca w górę ma zerowy moment bo ma zerowe ramię (względem punktu podparcia). Ciężar mg wytwarza jednak moment siły względem punktu podparcia: τ = r×F = r×mg
gdzie r określa położenie środka masy. Z iloczynu wektorowego wynika, że τ jest prostopadłe do r i do mg.
Zauważmy, że τ, L i r wirują dokoła osi pionowej z częstością precesji ωp.
Obliczymy teraz kątową precesję ωp. ![]()
Ponieważ ΔL << L, to mamy Δϕ ≅ ΔL/Lsinθ
Z równania (12.5) wynika, że ΔL = τΔt
Więc Δϕ ≅ τΔt/Lsinθ
Otrzymujemy więc ωp = Δϕ/Δt = τ/Lsinθ (12.14)
Moment siły jest równy
τ = rmg sin(180°-θ) = rmg sinθ
więc ostatecznie
ωp = rmg/L
prędkość precesji nie zależy od kąta θ i jest odwrotnie proporcjonalna do wartości momentu pędu.
Równanie (12.14) można zapisać w postaci wektorowej. Najpierw przepisujemy je do postaci
τ = ωpL sinθ
Widać, że po prawej stronie równania otrzymaliśmy wartość iloczynu wektorowego ωp×L. Tak więc ostatecznie wyrażenie wiążące prędkość kątową precesji z momentem siły i momentem pędu ma postać ![]()
Zjawisko precesji momentu magnetycznego (spinu) jest podstawą różnych technik doświadczalnych (NMR, EPR), które znalazły szerokie zastosowanie w badaniach, technice i medycynie.
43.Równowaga ciał sztywnych.
44.. Ruch harmoniczny prosty
Ruch, który powtarza się w regularnych odstępach czasu, nazywamy ruchem okresowym (periodycznym). Przemieszczenie cząstki w ruchu periodycznym można wyrazić za pomocą funkcji sinus i cosinus.
Siła harmoniczna
Działającą na ciało siłę, która jest proporcjonalna do przesunięcia ciała od początku układu i która jest skierowana ku początkowi układu, nazywamy siłą harmoniczną lub siłą sprężystości. Jeżeli obierzemy oś x wzdłuż przesunięcia, to siła harmoniczna jest wyrażona równaniem F = - kx (13.1)
gdzie x jest przesunięciem od położenia równowagi. To równanie opisuje siłę wywieraną przez rozciągniętą sprężynę o ile tylko sprężyna nie została rozciągnięta poza granicę sprężystości. To jest prawo Hooke'a.
Jeżeli sprężyna zostanie rozciągnięta tak aby masa m (zaczepiona do sprężyny) znalazła się w położeniu x = A, a następnie w chwili t = 0 została zwolniona, to położenie masy w funkcji czasu będzie dane równaniem x = Acosωt
Sprawdźmy czy to jest dobry opis ruchu. Dla t = 0, x = A tzn. opis zgadza się z założeniami. Z drugiej zasady dynamiki Newtona wynika, że
- kx = ma czyli - kx = m(dv/dt) wreszcie - kx = m(d2x/dt2) (13.2)
rozwiązaniem jest funkcja x(t), która ma tę właściwość, że jej druga pochodna jest równa funkcji ale ze znakiem "-". x = Acosωt dx/dt = v = - Aωsinωt (13.3) d2x/dt2 = a = - Aω2cosωt (13.4)
Podstawiamy ten wynik do równania (13.2)
(- kAcosωt) = m(- Aω2cosωt)
i otrzymujemy ω2 = k/m (13.5) x = Acosωt jest rozwiązaniem równania (13.2) ale tylko gdy ![]()
. Zwróćmy uwagę, że funkcja x = Asinωt jest również rozwiązaniem równania ale nie spełnia warunku początkowego bo gdy t = 0 to x = 0 (zamiast x = A).
Najogólniejszym rozwiązaniem jest x = Asin(ωt + ϕ) (13.6) gdzie ϕ jest dowolną stałą fazową. Stałe A i ϕ są określone przez warunki początkowe.
Wartości maksymalne (amplitudy) odpowiednich wielkości wynoszą:
dla wychylenia A
dla prędkości ωA (występuje gdy x = 0)
dla przyspieszenia ω2A (występuje gdy x = A)
Okres drgań
Funkcja cosωt lub sinωt powtarza się po czasie T dla którego ωT = 2π. Ta szczególna wartość czasu jest zdefiniowana jako okres T T = 2π/ω (13.7)
Liczba drgań w czasie t jest równa n = t/T
Gdy podzielimy obie strony przez t, otrzymamy liczbę drgań w jednostce czasu
![]()
Wyszukiwarka
Podobne podstrony:
Całość, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SEMESTR 2
Egzamin fizyka 31-35, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stop
do druku lool, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SE
1-5, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SEMESTR 2, F
Cwiczenie 53c, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SE
Cwiczenie 11i, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SE
kryształy egzamin 2009, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I st
Cwiczenie 32f, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SE
Cwiczenie 0f, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SEM
Wstep 0, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia, SEMESTR
pytania u komornickiego, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I s
Zadania bilanse, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia,
Projekt 2 - Ewa Litwinek, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I
Pytanianakolosach, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia
Układ MgO-Al2O3-SiO2, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stop
wyniki zaliczenia w I term. gr 3.x, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stac
Sprawozdanie JP, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarne I stopnia,
Tablica przedzialy Ufnosci 1, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stacjonarn
Metody badan odpornosci korozyjnej, Akademia Górniczo - Hutnicza, Technologia Chemiczna, Studia stac
więcej podobnych podstron