00098515

318 !. PUNKCIE ZMIENNEJ ZESPOLONEJ

Wprowadzamy z kolei okrąg JJ{z₀; g) ^c D_c. Na podstawie wniosku 2 z twierdzenia podstawowego Caoehy’ego, mamy

^ A(z)<fr = h(t)Hz    (lil ii®

(por. równość (III. 131)). Ocenimy całkę znajdującą się po prawej stronie tej równości. Ponieważ funkcja A(z) jest ciągła w obszarze domkniętym i ograniczonym D_e, wiec istnieje skończony be* górny

supiA(z)i = M    \

Oczywiście dla każdego okręgu K(r₀;o) •= O_e mamy

SupiMz)| < M

więc na podstawie twierdzenia o module całki dostajemy

|^yA(z)<fzj < M-2nf>    (HI.137J    i

Zwróćmy uwagę, że lewa strona równości (III. 136) nie zależy od g, natomiast prawa strona tej rów- • || ' ności ma na podstawie oceny (01.137) modut dowolnie bliski zeru, gdy g jest dostatecznie małą liczbą dodatnią. Wynika stąd, że    i Jw

h{t)dz=o

^C2>!l    ^ m-fw> _rf._₀ ■    '' _s '.J|

'I

ponieważ całka po prawej stronie tej równości istnieje. Na podstawie wzorów (HI. 131) i (IH.I2l)S||

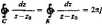
więc ostatecznie dostajemy równość (1II.13S), cod.    ;

Równość (III. 135) jest to tzw. wzór całkowy Catichy'ego. Ma on w teorii funkojtis zmiennej zespolonej wielkie znaczenie. Wzór ten został podany przez Caućhv’ECO;; w 1831 r.    '

Zauważmy, te krzywa Jordana Ccfli punkt z₀ e D_c, o których jest mowa w twierdzeniu o wzorze całkowym Caucby’ego, są dowolne. Z tego twierdzenia-, wynika więc, źe wartość funkcji holomorficznej /(z) w każdym punkcie z_a e l|| można wyrazić przez wartości tej funkcji na dowolnej kawałkami gładkiej kizywey Jordana CcJ, wewnątrz której znajduje się punkt z₀. Inaczej mówiąc, warto&*| funkcji holomorficznej /(z) aa krzywej C określają jednoznacznie wartości tej fanki# ; wewnątrz krzywej. Stanowi to bardzo ciekawą i głęboką właściwość funkcji raorficznych.    ’    ^v";jTj

Uwaga. Wzór [111.135) jest także prawdziwy, gdy założymy tylko ciągłość funkcji Kii w obszarze domkniętym i>_t oraz jej hólomorfianość wewnątrz tego obszaru.

A oto prosty przykład zastosowania wzoru całkowego Cauchy’ego.

Przykład. Obliczyć

&■    °°^5Z dz

aj; i) “ ^+ł

Przekształcamy funkcję podcałkową

cosz _ T+J    /(;)

z^s+l 2-j    z-j

Funkcja/(z) jest holomorfkzDa w pewnym obszarze jednospójnyro zawierającym okrąg _np. w półpłaszczyźnie Rer> ——, więc na mocy wzoru całkowego Cauchy’ego mamy

*f/n>    ‘    '    '    *

Pochodne wyższych rzędów. Niech/(z) oznacza funkcję holomorficzną w obszarze D. Rozwalmy dowolny punkt z_a s D i okrąg łC(z₀; 2d) leżący wraz ze swym wnętrzem w tym obszarze. Wykażemy, że

2ńj T (z—z₀)²

w tym celu rozważmy iloraz różnioowy

ograniczając &ie do przyrostów Az spełniających warunek [Az! < d (rys. m.41), co oczywiście nie zmniejsza ogólności rozumowania. -    ‘

Wartości funkcji/(z_n+dz) i/(r₀) wyrażamy za pomocą wzoru całkowego Cauchy’ego, przyjmując okrąg K za krzywą, po której całkujemy; stąd

/(Zo+^z)-/(Zo) _

W** f^f(Z) [ z-fe+dr) z-z„ ] f(z)dz

dz =

2*J J Jż-(Zo+żlzjKz-7|)). la tę równość, mamy następnie

. f(z_a+Az)—f(z₀)__i f f{z)dz    Az f

Az    2rsf J (z—Zd)*    2»f 7 l

2*// b-fZo+dz)](z-_ł8)* Na podstawie twierdzenia o module całki dostajemy (por.-rys. 111.41)

(zo+Az)J(z-z₀y 1 2rt d(2dy'