53313 str037 (5)

5 5. POCHODNA FUNKCJI ZMIENNEJ ZESPOLONEJ 37

wychodzącą z punktu w₀ = /(z₀) = /[z(/₀)] (rys. 1.6). Na mocy twierdzenia o różniczko' waniu funkcji złożonej z (5.5) wynika

(5.6)

Podstawiając w (5.6) t = t₀, mamy

(5.7)

^'Oo) =/'(z₀)z'(f o)-

Styczna do krzywej C o równaniu (5.4) w punkcie z₀ tworzy z osią rzeczywistą kąt

(5.8)

<p = argz'(f₀).

Styczna zaś do krzywej r o równaniu (5.5) w punkcie w₀ tworzy z osią rzeczywistą kąt

(5-9)

Wobec tego z (5.7) wynika, że

<P = argw'(f₀).

arg w' (f₀) = arg/' (z₀) + arg z' (t₀),

(5.10)

<P = arg f\z₀) + (p,

arg/'(z₀) = 4>-ę>.

Wzór (5.10) orzeka, że argument pochodnej w dowolnym punkcie z₀ równa się kątowi obrotu, jakiego doznaje styczna w punkcie z₀ do łuku regularnego C przechodzącego przez ten punkt przy odwzorowaniu (5.3).

Z istnienia pochodnej funkcji (5.3) w punkcie z₀ wynika, że

(5.11)

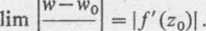
x-*ro Z Z₀

Równość (5.11) oznacza, że dla każdego s>0 istnieje takie <5>0, iż

(5.12)

Innymi słowy, odległości punktów z dostatecznie bliskich punktu z₀ wzrastają przy odwzorowaniu (5.3) w stosunku dowolnie mało różniącym się od modułu pochodnej /'(z₀). Weźmy teraz pod uwagę dwa łuki regularne C_x i C₂ wychodzące z punktu z₀. Niech<p_t i q>₂ oznaczają kąty, jakie styczne do krzywych C_t i C₂ w punkcie z₀ tworzą z osią rzeczywistą Ox. Niech dalej r, i f₂ oznaczają krzywe wychodzące z punktu w’₀ =/(z₀), które są obrazami odpowiednio łuków C₂ i C₂ za pomocą funkcji (5.3). Oznaczamy przez i <P₂ kąty, jakie styczne odpowiednio do krzywych i r₂ w punkcie vr₀ tworzą z osią rzeczywistą Ou (rys. 1.7). Na mocy (5.10) mamy

Ostatnia równość orzeka, że kąty między krzywymi Cj i C₂ w punkcie z₀ oraz ich obrazami r_t i r₂ w punkcie u’₀ = /(z₀) przy odwzorowaniu (5.3) są sobie równe i mają te same zwroty.