10036 str020 (5)

20 1. ELEMENTY TEORII FUNKCJI ZMIENNEJ ZESPOLONEJ

Otoczeniem pierścieniowym punktu z₀ nazywamy zbiór punktów z, spełniających nierówność

0<|z-z_o|<)\

gdzie r>0.

W interpretacji geometrycznej otoczenie pierścieniowe punktu z₀ przedstawia wnętrze koła o środku w punkcie z₀ i promieniu r po usunięciu z niego punktu z₀ (rys. 1.4).

Jeżeli każdej liczbie zespolonej z należącej do pewnego zbioru płaskiego E (np. do obszaru) przyporządkujemy pewną liczbę zespoloną

(3.1)    w=/(z),

to mówimy, że w zbiorze E została określona funkcja zespolona f (z) zmiennej zespolonej z. Zbiór E nazywamy wtedy polem (dziedziną) funkcji /(z), zbiór zaś £,, składający się ze wszystkich wartości funkcji (3.1), nazywamy jej zakresem (przeciwdziedziną). Mówimy także, że wzór (3.1) wyznacza odwzorowanie (przekształcenie) zbioru E na zbiór E_t. Funkcję (3.1) nazywamy jednoznaczną w zbiorze E, jeżeli każdej wartości ze E odpowiada tylko jedna wartość W dalszych rozważaniach funkcję jednoznaczną nazywać będziemy krótko funkcją. Mówimy, że funkcja /(z) ma w punkcie z₀ zbioru E granicę g, jeżeli dla każdego ciągu z„-»z₀, ale o wyrazach różnych od z₀, odpowiedni ciąg wartości funkcji f(z„)-+g. Zapisujemy to w następujący sposób:

lim f(z) = g lub /(z) -♦ g.

Z-*Zo    Z-*ZQ

Definicja ta nie różni się formalnie od określenia granicy funkcji zmiennej rzeczywistej. Wobec tego pozostają prawdziwe znane twierdzenia o granicy sumy, różnicy, iloczynu oraz ilorazu dwóch funkcji f(z) oraz g(z), mających granice skończone w punkcie z₀. Podstawiając we wzorze (3.1) z = .r+/y, w = u+iv, możemy funkcję (3.1) napisać w postaci

u + iv = f(x + iy)

lub, co na jedno wychodzi, w formie

u + iv = u (x, y) + iv (x, >■),

gdzie

f(x + iy) = u(x, y) + iv(x,y).

Funkcje u(x, y) oraz v(x, y) nazywamy odpowiednio częścią rzeczywistą oraz urojoną funkcji (3.1)

Twierdzenie 1. Jeżeli funkcja w = /(z) = u(x, y) + iv(x, y) ma granicę g = g_} +ig₂ w punkcie z₀ = x_<} + iy₀, to część rzeczywista u(x, >>) oraz urojona v(x, y) mają odpowiednio w punkcie (x₀, _y₀) granicę g_y oraz g₂ i odwrotnie.

Funkcję zmiennej zespolonej /(z) nazywamy ciągłą tv punkcie z₀, jeżeli wartość funkcji /(z₀) w tym punkcie jest równa granicy funkcji w tym punkcie, czyli jeżeli

lim f(z) =f(z₀).

Z-+ZO

Funkcję/(z) nazywamy ciągłą w zbiorze E, gdy jest ciągła w każdym punkcie tego zbioru.

Twierdzenie 2. Jeżeli z₀ = x₀ + iy₀, to zarówno c (x₀,y₀) i odwrotnie.

Zadania przykładowe Zadanie 3.1. Określić | a) w = z² +1, b) w =

Rozwiązanie, a) Bie:

(O

Zauważamy od razu, że fu: polem jest cała płaszczyzna mamy

(2)

Porównując po obu stron.

b) Funkcja

(3)

jest określona dla wszystl polem naszej funkcji jest pl W celu znalezienia części stępująco:

(4)    w Podstawiając w = u + ii', i

u + iv

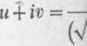
(5)